Преобразование спинового момента в орбитальный момент в лазерном пучке

Интерес к действиям в реальном масштабе времени, обусловленным орбитальным моментом импульса световых пучков, вызван многообещающими возможностями применения этого явления в квантовых компьютерах, криптографии и квантовой телепортации [1–3]. Информация может быть декодирована с помощью перемножения набора состояний, так как фотон несет большое количество информации, распределенной по его спиновым и орбитальным квантовым состояниям [4]. Кроме того, операции с орбитальным моментом позволяют увеличить количество параметров, по которым можно модулировать оптические пучки, а именно, любая информация, содержащаяся в сигнале, может быть декодирована не только в фазу, интенсивность, поляризацию или частоту света, но также в его орбитальный момент. В итоге развитие прямых методов, позволяющих производить действия с орбитальным моментом, дает новые возможности для применения квантовых свойств фотона. Однако достаточно сложно найти подходящую среду для преобразования спинового момента фотона в орбитальный в реальном времени.

В работе [5] рассмотрена возможность совершения такого преобразования благодаря эффекту Поккельса, возникающему в случае, когда в кристалле LiNbO 3 создается внешнее электрическое поле конической формы. Существует ряд публикаций, в которых демонстрируется возможность преобразования спинового момента в орбитальный с топологическим зарядом m = ± 2 при помощи нематических жидких кристаллов [6]. В [7] представлено оптическое устройство под названием q -plate, представляющее из себя двулучепреломляющую пластинку (сделанную, например, из нематического жидкого кристалла), которая позволяет наблюдать преобразование спинового момента светового пучка в орбитальный с топологическим зарядом ± 2.

Поиск новых сред, которые позволяют преобразовывать спиновый момент в орбитальный, является актуальной задачей. Оптическое волокно может быть именно такой средой.

Таким образом, целью данной работы является исследование возможности преобразования спинового момента пучка с ± 1 в орбитальный момент пучка m ± 1 при распространении излучения в оптическом волокне.

Анализ распространения циркулярно поляризованного излучения в оптическом волокне

Рассмотрим распространение излучения в оптическом волокне со ступенчатым профилем показателя преломления [8].

Пусть на вход волокна падает циркулярно поляризованный пучок Гаусса со спиновым моментом с =+ 1:

Краткие сообщени^

^E ( r ) = ( ^e x ⁺ i ^e y ) E O ^eXP

( „ 2 A

r

где r ² = x ² + y ² . Попадая в оптическое волокно, пучок распадается на вытекающие и направляемые моды. Вытекающие моды не рассматриваются, так как полагаем, что до выходного торца волокна они не дойдут. Поле направляемых мод на входе в оптическое волокно имеет следующий вид:

Е + (r ”, z = 0 ) = ( е x + iе y )• e-”ZC-1NFN (r) + Z ZC-,”   (r) + ZZC+,m,(r) -, m ^1 N

mN

где коэффициенты C - 1 _N и C ₊ 1 _N определяют вклад мод e + _{m N} ( r , ” ) и e + _{m N} ( r , ” ) в световое поле на входе в волокно. Тогда в волокне возбуждаются моды с положительным ( + m ) и отрицательным ( - m ) топологическим зарядом, и поле представляет собой суперпозицию полей с разными орбитальными моментами. На выходе из волокна имеем следующее распределение поля для направляемых мод:

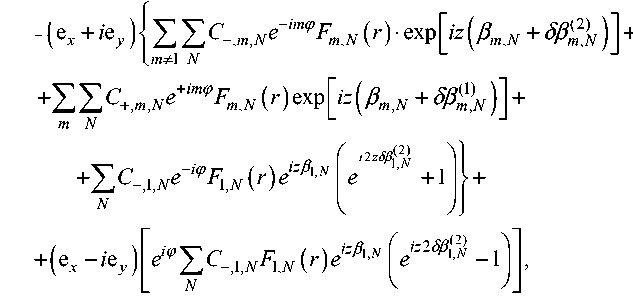
. m ^1 N mN

- 2 ^гв$

■ Z C - ,1, N e ^- ” F 1, n ( r ) e

+

N

+ ( e x - i e , ) e ”” Z

где 5j3 miN — поляризационная поправка к константе распространения моды с индексами m и N , F_{m N} ( r ) — радиальная функция. Аналогичные выражения можно записать и для случая, когда на вход волокна падает излучение со спиновым моментом с = - 1.

Из выражения (1) следует, что на выходе из волокна появляется излучение с противоположным спиновым моментом с с = - 1 («чужая» поляризация) [8, 9].

Если на выходе из волокна поставить «циркулярный анализатор», пропускающий циркулярно поляризованное излучение со знаком, противоположным знаку с на входе в волокно, то через него пройдут только соответствующие моды с m = 1. Этот анализатор состоит из четвертьволновой пластинки и поляризатора. При помощи пластинки выделяются две ортогональные компоненты циркулярной поляризации, преобразуя их в линейно поляризованные. Поляризатор выделяет поле, описываемое последним членом в уравнении (1).

Поле пучка, прошедшего через «циркулярный анализатор», описывается последним членом в сумме (1):

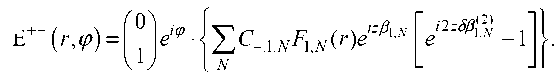
„ i ^{2 Z}  1

e - 1

Множитель e ” свидетельствует о присутствии положительного орбитального момента с топологическим зарядом + 1 . Аналогичное выражение можно записать и для случая, когда на вход волокна падает излучение со спиновым моментом с с = - 1. Таким образом, в рассматриваемой схеме происходит преобразование спинового момента пучка в единичный орбитальный момент того же знака, то есть, спиновый момент с с = + 1 преобразуется в орбитальный с m = + 1, а спиновый момент с с = - 1 в орбитальный с m = - 1. Из выражения (1) следует, что эффективность преобразования определяется долей вклада мод с m = ± 1, поэтому, чем меньше мод распространяется в оптическом волокне, тем выше эффективность преобразования.

Бо^ьшаков М.В., Гусевa A.B.,                               П^еоб^азование спинового момента

Кундикова Н.^., Попков И.И.                          в о^бита^ьный момент в ^азе^ном пучке

Эффективность преобразования также зависит и от длины волокна. Из выражения (2) легко получить зависимость интенсивности излучения I +- от длины волокна. В случае такого маломодового оптического волокна, когда m = 1 и N = 1, эта зависимость носит периодический характер:

I ⁺ - ( r, ^ ) = E ^+- ■ (E ⁺ - ) * = ( C -_дд F_u (r )) 2 [ 1 - cos(2 z ^ ?) ] .                     (3)

Максимальное значение интенсивность I ⁺ приобретает при длинах волокна:

_ п(2n -1) n = 25/3(2 , где n – целое число. Следовательно, можно подбирать длину оптического волокна так, чтобы эффективность преобразования спинового момента в орбитальный была максимальной.

Таким образом, если на вход волокна со ступенчатым профилем показателя преломления подавать циркулярно поляризованное излучение с определенным знаком с , а на выходе волокна выделять «циркулярным анализатором» циркулярно поляризованное излучение противоположного знака, то прошедшее излучение будет представлять собой световую волну, обладающую единичным орбитальным моментом того же знака, что и с . Смена знака с на входе волокна при соответствующем изменении знака «циркулярного анализатора» приводит к смене знака орбитального момента. Наличие орбитального момента подтверждается присутствием спирали на интерференционной картине при сложении полученного пучка с гауссовским пучком. Направление раскручивания спирали зависит от знака орбитального момента.

Экспериментальное исследование преобразования спинового момента пучка в орбитальный

Для экспериментального преобразования спинового момента лазерного пучка в орбитальный было выбрано оптическое волокно с диаметром сердцевины 2 р = 9 мкм, со ступенчатым профилем показателя преломления n ( r ):

₍ . Г neo , r / Р <  ¹ n ⁽ r ) = 1               ,

I n e/ , r / Р >  ¹

где r = | r |,( x , y ) = r - поперечные координаты, p - радиус сердцевины, n_eo и n_e/ - показатели преломления сердцевины и оболочки. Длина волокна составляла 259 мм. Схема экспериментальной установки представлена на рис. 1.

Рис.1. Оптическа^ схема экспериментальной установки

Излучение He-Ne лазера с длиной волны X = 632 нм, пройдя через призму Глана, попадало на пластинку X 4, при помощи которой формировалось циркулярно поляризованное излучение. Затем излучение фокусировалось объективом на входной торец оптического волокна. Вышедшее из волокна излучение коллимировалось объективом и проходило через пластинку X 4, а затем через поляризатор, преобразуясь в линейно поляризованное. Изображение наблюдалось при помощи ПЗС-матрицы. Пластинка X 4 и поляризатор вместе образуют «циркулярный анализатор», при помощи которого выделялось излучение с нулевым спиновым и единичным орбитальным моментом.

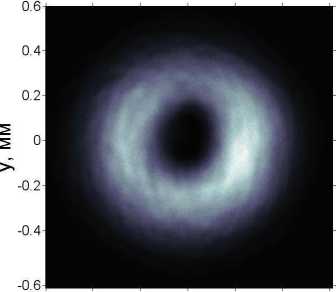
-0.6   -0.4    -0.2     0     0.2    0.4    0.6

Рис. 2. Распре^еление интенсив- ности в поперечном сечении пучка, проше^шего через оптическую схему, пре^ставленную на рис. 1

На рис. 2 представлено экспериментально зарегистрированное распределение интенсивности в поперечном сечении

Краткие сообщени^

пучка после прохождения «циркулярного анализатора». Как видно из рис. 2, распределение интенсивности имеет вид однородного кольца, что соответствует выражению (3).

Для проверки наличия орбитального момента регистрировалась интерференционная картина исследуемого пучка и пучка Гаусса. Как указывалось выше, интерференционная картина двух пучков должна представлять собой спираль, направление раскручивания которой определяется знаком топологического заряда. В случае, если m = +1, спираль раскручивается по часовой стрелке, а если m = -1, то наоборот – против часовой. На рис. 3 представлено распределение интенсивности в интерференционной картине для случая, когда на вход волокна падает циркулярно поляризованное излучение со спиновым моментом о = +1.

-0.8 -0.6 -0.4 -0.2     0     0.2    0.4    0.6    0.8

X, мм

Рис. 3. Распре^еление интенсивности в интерференционной картине полученного пучка с пучком Гаусса

На рис. 3 отчетливо видна спираль, направление раскручивания которой (по часовой стрелке) свидетельствует о том, что исследуемый пучок имеет орбитальный момент m = + 1.

Таким образом, на основе анализа распространения циркулярно поляризованного излучения в оптическом волокне со ступенчатым профилем показателя преломления продемонстрирована возможность преобразования спинового момента пучка с о ± 1 в орбитальный момент пучка с m ± 1.

Показано, что эффективность преобразования выше для маломодовых волокон. В зависимости от длины волокна эффективность может изменяться от 0 до некоторой максимальной величины, значение которой определяется количеством мод, распространяющихся в волокне и условиями ввода излучения в волокно.

Возможность преобразования спинового момента пучка с о ± 1 в орбитальный момент пучка с m ± 1 доказана экспериментально.