Приближенные цифровые дели роста и продуктивности растений (обзор)

Введение . Изучению процесса роста растений и их продуктивности посвящена обширная литература (десятки тысяч статей, книг и монографий), некоторые указания литературы по данной теме можно найти в известных монографиях [2–10]. Характерной особенностью работ по данной проблеме является, в основном, описание эффективных результатов экспериментальных исследований для разных территориальных районов, климатических условий, разных сельскохозяйственных культур и растений; теоретических исследований по данной проблеме значительно меньше [11–16]. Актуальность и важность развития теоретических исследований процессов роста растений и их продуктивности особенно ясно отмечал академик. В.С. Шевелуха в монографии [17]: в настоящее время назрела необходимость в активной разработке экологии роста, изучении общих закономерностей на уровне целостного организма , выявлении форм взаимосвязи роста с фотосинтезом, дыханием и другими физиологическими процессами, расшифровке генетических и физиолого-биохимических механизмов регуляции и саморегуляции роста и развития растений. Весьма актуальными являются также исследования по созданию математических моделей роста и разработке новых методов его прогно- 80

зирования, изучению периодичности и ритмичности роста растения в целях выявления регуляторных механизмов и поиска новых путей повышения продуктивности растений и посевов ([17], стр. 4). По мнению В.С. Шевелухи, рост, как процесс, отражающий общий итог всех функциональных и метаболических изменений в растениях и наиболее тесно коррелирующих с ходом накопления ими биомассы, может и должен использоваться в качестве универсального индикатора при оценке физиологического состояния растений, а также при организации агрономического контроля за посевами и ходом накопления ими урожая.

Характеризуя современное состояние развития моделей динамики и моделирования развития древостоев, авторы краткой критической статьи [18] отмечают следующее: модели динамики состояний в статике в виде многочисленных таблиц продуктивности по классам возраста, называемых « таблицами хода роста » полных и модальных древостоев, классифицированы по классам бонитета и по типам леса. Они сыграли выдающуюся роль в оценке производительности наших лесов, однако процесс развития древостоев они не отражают. Все очевиднее становится положение что системный анализ древостоев имеет перекос в сторону изучения их состояний в статике, выхваченных из «движения» древостоев в их биологическом времени; драма их развития осталась почти не изученной , надо признать это и идти дальше. В связи с этим нужны модели развития древостоев , описывающие в табличной или иной форме сам процесс развития – от возраста формирования древостоя до начала его распада, с выделением фаз прогресса и регресса. Для моделей важно постулировать интегральные свойства ценоза, например константы для массы хвои и объемов крон, имеющих ясный биологический смысл в виде неких пределов этих показателей при заполнении полога древостоя биомассой ([18], с. 66).

Материалы и методы. Основатель экспериментальной физиологии растений Юлиус фон Сакс (Julius von Sachs, 1832– 1897 гг.) впервые в работах 1856–1865 гг. [19; 20] подробно исследовал ход ростовых процессов разных растений в виде S-образной кривой роста размеров (высота, диаметр) и сухой массы разных частей (листья, стебель, корни) растений. Ю. Сакс впервые установил три главных периода развития растения: 1 период – « восходящая ветвь », 2 период – средняя часть кривой роста – « прямолинейная ветвь », 3 период – « нисходящая ветвь » ([19], с. 365). Кривая роста растения, начинаясь от нуля, поднимается вверх до точки перелома, после точки перегиба кривой наступает период прямолинейного роста, а затем скорость роста уменьшается, рост растения асимптотически приближается к некоторому максимальному значению [19; 20].

Ф.Ф. Блэкман (F.F. Blackman) с сотрудниками для разных растений и разных условий экспериментально подтвердил результаты Ю. Сакса [21–24]. В работе 1895 г. [21], в частности, впервые описан новый метод исследования обмена углекислоты для разных растений (овощей), во второй части статьи [22] изложены результаты экспериментального исследования газообмена между листьями и атмосферой, в работе 1905 г. [23] впервые представлены результаты экспериментального изучения усвоения углекислого газа листьями растений при естественной радиации (освещении), в статье 1911 г. [24] впервые проведено экспериментальное изучение процесса ассимиляции растений при разной концентрации углекислого газа и температуры.

Д.А. Сабинин в 1929–1963 гг. выполнил важные экспериментальные и теоретические работы по исследованию физиологии роста и развития растений

[25–30]. Отмечая важность первых результатов по исследованию общего характера кривых роста растений, полученных Ю. Саксом (J. Sachs, 1873 г.), профессор Д.А. Сабинин специально отмечает, что формулировка основных математических закономерностей процесса роста растений наталкивается на значительные, пока еще непреодолимые трудности ([29], стр. 11). Д.А. Сабинин одним из первых на основе механизма поступления веществ в клетку растения [27; 30] приводит научно обоснованное определение понятия « рост »: рост растения – это процесс новообразования элементов структуры организма ; под элементами структуры при этом понимаются основные части клетки: ядро, пластиды, хондриосомы, протоплазма, мицеллы, образующие клеточную оболочку, клетки тканей и органы растений ([30], стр. 282–283). Изучая механизм минерального питания растений, Д.А. Сабинин [26–28] экспериментально установил, что процесс поглощения воды, а также перемещение воды и питательных веществ в растении происходят за счет взаимодействия протопласта с ионами окружающей среды и клеточного сока; изменения в ионном составе окружающей среды или клеточного сока приводит к изменению в направлении и скорости тока воды и питательных веществ при их обмене между клеткой и наружной средой, т. е. поглощении ионов на поверхности раздела, что определяет процесс адсорбции. Опытами установлено, что адсорбция – процесс, имеющий предел: состояние адсорбционного насыщения ([28], стр. 167). На рисунках 1, 2 показаны опытные кривые поглощения водного раствора метиленового синего (рис. 1) и адсорбции ионов свинца почвы (рис. 2) корневой системой пшеницы ([28], рис. 61, 62, стр. 169).

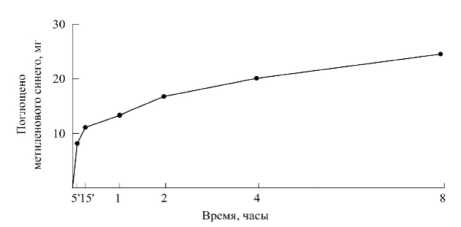
Рисунок 1 - Адсорбция метиленового синего корневыми системами пшеницы ([28], рис. 62, стр. 169)

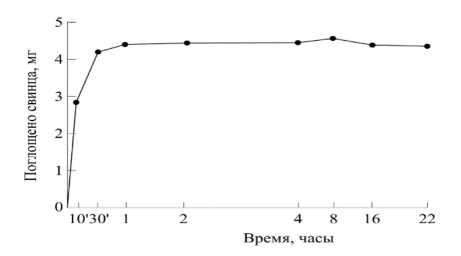
Рисунок 2 - Адсорбция свинца корневыми системами пшеницы ([28], рис. 61, стр. 169)

Опытами установлено, что поглощение воды не может вызвать поглощение солей, а поглощение ионов протопластом может вызвать изменения в обводненности протоплазматических структур растения; не существует прямой связи между количеством транспонированной растениями воды и количеством солей, поглощенных из раствора, окружающего корневые системы; отсутствует связь между объемом поглощенной воды и объемом растворенных веществ из среды, окружающей корни, что свидетельствует о том, что из корневых систем выделяются в наружную среду ионы и, следовательно, в питании растений за счет почвы источниками снабжения корневых систем ионами солей могут быть водная фаза почвы и коллоидные частицы почвы, несущие ионы в адсорбционно-связанном состоянии : корни ячменя, выращенного в водной культуре при невысоком содержании калия в питательной среде, стойко удерживают калий при погружении в дистиллированную воду или растворы со-82

лей, но при взаимодействии с суспензиями частиц бентонита происходят значительные изменения содержания калия в корнях ([28], стр. 219–222). Характеризуя важную роль фотосинтеза в жизни органического мира, Сабинин Д.А. отмечает, что совокупность жизненных проявлений любого живого существа, все виды работы, роста растений, движений, химических превращений и другое, основываются на использовании химической энергии органических соединений, где первичный синтез органических веществ протекает в хлорофиллоносных растительных клетках и организмах, который является единым во всем органическом мире [28; 29]; фотосинтез оказывается замечательным процессом, при котором деградация энергии в одной части солнечной системы вызывает поднятие ее уровня в другой части системы. Экспериментально установлено (К.А. Тимирязев, В.Н. Любименко, F.F. Blackman и др.), что зависимость скорости фотосинтеза от напряженности света сначала является линейной, затем при увеличении напряженности света до определенной точки перегиба она растет, а после точки перегиба перестает увеличиваться, принимая определенное максимальное значение (рис. 3).

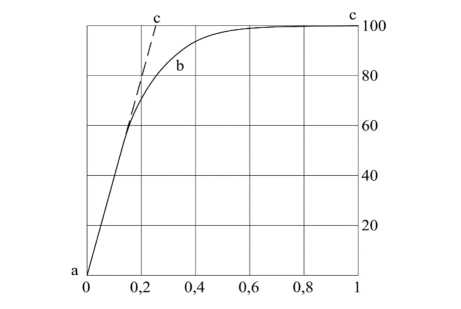
Рисунок 3 - Зависимость скорости фотосинтеза от напряженности света На оси абсцисс – напряженность света в долях от полного солнечного освещения, на оси ординат – скорость фотосинтеза в процентах от максимальной величины ([28], рис. 109, стр. 327)

Наличие точки перегиба ( b ) на кривой зависимости скорости фотосинтеза от напряженности света объясняется недостатком в основном углекислоты, или « ограничивающими факторами ».

На рисунке 4 показаны опытные кривые зависимости скорости фотосинтеза от напряженности (Harder, 1921), из которых видно, что при низкой концентрации КНСО 3 увеличение скорости фотосинтеза является малым, однако эти эксперименты показали « проявление взаимосвязи факторов » на фотосинтез.

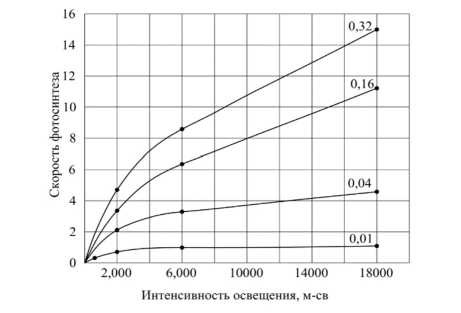
Рисунок 4 – Зависимость скорости фотосинтеза мха Fontinalis от интенсивности света при различном содержании углекислоты. Цифры на кривых указывают процент содержания КНСО 3 в растворе ([28], рис. 111, стр. 329)

На рисунке 5 показаны теоретические кривые зависимости скорости фотосинтеза от концентрации углекислоты (Blackman, 1905), которые хорошо иллюстрируют «взаимосвязь факторов» при фотосинтезе ([28], стр. 328).

Можно отметить, что кривые, показанные на рисунках 1–5 выше, характеризующие процесс поглощения растворов и питательных веществ корневой системой (рис. 1, 2), процесс фотосинтеза (рис. 3– 5), являются подобными, что может свидетельствовать об общности механизма роста и развития растений на планете Земля; подобные опытные кривые при питании разных растений и фотосинтеза в разных условиях установлены многими известными исследователями [31–36].

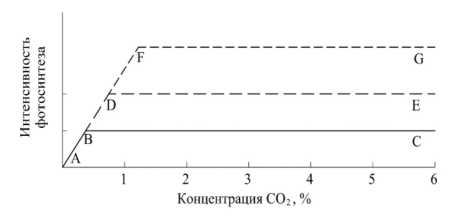
Рисунок 5 – Схема действия ограничивающих факторов при фотосинтезе АВС – интенсивность фотосинтеза при низкой напряженности света (ограничивающий фактор); BDE – то же при средней напряженности света; DFG – то же при высокой напряженности света ([28], рис. 110, стр. 328)

Определяя связь фотосинтеза и урожая, Д.А. Сабинин [28; 29] отмечает, что нет прямого соответствия между изменением фотосинтеза при переходе от белого света к свету определенных участков спектра и соответствующим изменением в накоплении растениями сухого вещества; эффективность фотосинтеза связана не с наличием органических веществ в растении вообще, а только некоторых из них, какими являются определенные компоненты ядра и протоплазмы, поэтому для процесса роста растения важнейшее значение имеет не прирост сухого вещества, а характер продуктов фотосинтетической деятельности растения, и в этой области еще до сих пор неразрешенным является вопрос о фотосинтетической деятельности листа. Наиболее значимым, фундаментальным результатом в физиологической теории роста растений Д.А. Сабинина [5; 27–29] является обоснование схемы постепенных изменений меристематических зачатков вегетативных органов побега растений. Опытами установлено, что весь цикл роста S-образной кривой роста чайного листа занимает 10 пластохронов и в период окончившейся экспоненциальной фазы роста на побеге происходит образование органов возрастающих размеров и увеличивающейся расчлененности; побег в это время находится в экспоненциальной фазе роста, и между началом развертывания листа и окончанием детерминации происходит три пластохрона на логарифмической части кривой роста, поэтому кривая роста побегов носит сигмоидный характер (рис. 6).

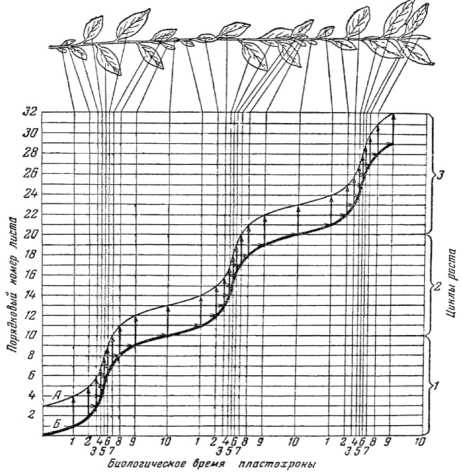
Рисунок 6 – Соотношение периодов видимого роста и детерминации зачатков листьев (схема) ([29], стр. 134, рис. 34) А – число зачатков листа, прошедших детерминацию; Б – число листьев, имеющихся на побеге. Горизонтальные стрелки указывают, из какого зачатка листа образовался данный лист. Вертикальные стрелки указывают, какой зачаток проходит детерминацию при появлении данного листа. Кривые даны для побегов, имеющих три цикла роста (ориг.)

Характеризуя математические модели роста растений, Д.А. Сабинин [28; 29] отмечает модель Т.Б. Робертсона (T.B. Robertson, 1923) [37] в виде следующего обыкновенного дифференциального уравнения первого порядка:

dW dt

= k 1 W ( A - W )

(уравнение (1), стр. 14, [29]), где W – вес, или размер растущего образования;

t – время;

А – конечная предельная величина, достигаемая при росте растения; k 1 – постоянный коэффициент ( коэффициент роста ).

Решение основного уравнения роста растения Т.Б. Робертсона принимается в виде:

1 W k = —log---

• ¹   t - t 1 ⁶A - W

(уравнение (3), стр. 15, [29]), где t 1 – время, когда текущее значение веса ( W ) равно половине предельной величины 2 W = А .

В монографии Д.А. Сабинин [29] специально отмечает, что уравнение Т.Б. Робертсона, дающее в ряде случаев значения для хода кривой роста, хорошо совпадающие с найденными значениями, лишено теоретической основы и может представлять интерес лишь как средство определения значения ряда промежуточных точек, а практическая его ценность в сильной степени умаляется необходимостью для его применения заранее знать две величины: А, t1 – знание этих двух величин предполагает достаточное представление о ходе кривой роста ([29], стр. 15). Отметим важное значение работы, в которой изложены результаты изучения     влияния     азотистых     и фосфорнокислых удобрений на урожай хлопчатника [25], опубликованной в 1931 г. В этой статье впервые приведены результаты изучения действия азотистых и фосфорнокислых удобрений по методике Э.А. Митчерлиха (E.A. Mitscherlich, 1909) для условий Средней Азии. В основе методики Э.А. Митчерлиха лежит представление о единообразной функциональной зависимости от отдельных факторов [25; 38–43]. В упомянутой статье [25] специально отмечается, что вся совокупность имеющихся в нашем распоряжении факторов заставляет признать, что мы еще не знаем уравнения урожая; до работ Митчерлиха давать ответы на во- просы о количественной зависимости урожая в каждом отдельном случае приходилось на основе абсолютной и процентной разницы контрольных и опытных растений, и такое положение приводило к накоплению громадного цифрового материала, собственно говоря, совершенно бессвязного, не поддававшегося ни обобщениям, ни анализу. Э.А. Митчерлих дал удачную интерполяционную формулу, и в хаос фактов было внесено организующее начало закономерности [25; 30]. Согласно Э.А. Митчер-лиху [38; 43] урожайность (у) и прирост урожая пропорциональны недостатку урожая до максимальной его величины (А), и, следовательно, можно записать основное уравнение первого порядка в обыкновенных производных:

dy = ( A - у k dx

(уравнение (1), стр. 540 статьи [38], уравнение (1), стр. 213 монографии [43]).

Решение этого уравнения можно записать в виде:

log ( A - y ) = log ( A ) - kx (уравнение (2), стр. 540 статьи [38], уравнение (5), стр. 24 монографии [43]).

Максимальное значение урожая ( А ) рекомендуется находить по формуле:

A = y 2 ^- У і y 3

• ²    y 2 ^- У 1 - y 3

(формула (4), стр. 540 статьи [38], формула без номера, стр. 392 монографии [43], формула без номера на стр. 477 в книге [30]), где у1, у2, у3 – опытные значения урожая, которые определены через равные интервалы фактора роста так, что: х3 – х2 = х2 – х1 и у1 = у(х1), у2 = у(х2), у3 = у(х3).

В статье [25] приведены следующие данные по урожайности хлопчатника (табл. 1). По методике Э.А. Митчерлиха [38; 43] установлено следующее уравнение:

log(100 - y) = log(100)- 0,104(x + 0,38)

(уравнение без номера, стр. 478, [30]), результаты расчетов по этому уравнению приведены в предпоследнем столбце таблицы 1.

Таблица 1

Урожайность хлопчатника ([25], стр. 478)

№№ п/п	Доза азота, г ( х i )	Урожайность
		опыт, г/сосуд ( у i )	расчет, г/сосуд у ( х i )	расчет, г/сосуд
1	0,75	23,57	23,62	23,570
2	1,50	36,21	37,32	36,210
3	2, 2 5	50,99	46, 6 7	48,123
4	3,00	61,53	55,43	62,634
5	6,00	77,67	78,22	79,630

Авторы статьи [25] отмечают, что: можно считать полученное совпадение опытных и расчетных значений урожая достаточно близким ([30], стр. 478) (в последнем столбце таблицы 1 приведены результаты расчетов по новой математической модели урожайности ). Д.А. Сабинин одним из первых в 1934 г. отмечал недостатки существующих моделей роста растений, в которых не учитывались особенности развития клеток : до сих пор мы занимались рассмотрением результатов работ по росту растений, в которых этот процесс учитывался по изменениям, протекавшим в громадном количестве клеток, т. е. интегрально. Микроскопические измерения позволяют делать вывод не только о новообразованиях микроскопических , но и изменении субмикроскопических элементов структуры организма растений, в этом случае важно исследовать значение отношения: объем ядра : объем клетки ; уменьшение этого отношения, идущего вплоть до остановки роста клетки характерно практически для всех растений. Дж. С. Хексли (J. Huxley, 1932) в фундаментальной большой монографии [44] с физиологических позиций обосновал применение « уравнения относительного роста » для исследования изменений частей растущего растения и в целом роста растения:

y = bx k

(уравнение (9), стр. 27, [29]; уравнение без номера, стр. 297, [30]), где у – вес органа, или части растения;

• b , k – постоянные коэффициенты;

х – вес всего органа, минус у ;

k – показатель относительного роста.

Уравнение относительного роста Дж. С. Хексли можно записать в виде:

log y = log b + k log x (уравнение (10), стр. 28, [29]; уравнение без номера, стр. 298, [30]), значения постоянных коэффициентов « b » и « k » определяются методом наименьших квадратов по фактическим (опытным) данным.

По мнению Д.А. Сабинина: уравнение относительного роста Дж. С. Хексли приложимо к изменению соотношений количественных признаков химического состава организма; применение уравнения относительного роста позволит исследовать закономерности стадийных изменений разных растений и их органов (частей) ([30], стр.     298–299).

С.О. Гребинский в 1961 г. опубликовал важную теоретическую работу, посвященную росту растений на основе современной клеточной теории строения организмов [45]. Рост стебля растения определяется процессом роста клетки, который состоит из трех основных этапов (фаз): 1) новообразование клетки путем деления; 2) фаза растяжения клетки (собственно рост); 3) фаза дифференцировки клетки [45]. Новообразование клетки происходит путем деления ядра клетки, которое приводит к удвоению числа клеток и увеличению ядерного вещества – нуклеопротеидов. Новообразование клетки определяется наличием ядра: если лишить клетку ядра, то она не делится ([45], стр. 16); причины, вызывающие наступление клеточного деления до сих пор не выяснены ([45], стр. 16). В фазе растяжения клетки происходит рост клеточной оболочки и синтез протоплазмы, которые приводят к образованию вакуоли и увеличению объема протоплазмы. Различают равномерный, верхушечный, вставочный и скользящий рост клетки ([45], стр. 19); растительная клетка растет не как единое целое: на разных участках растения имеются растущие клетки и клетки, закончившие рост. Фаза дифференцировки определяется процессом формирования клеточной оболочки, поступлением воды и увеличением объема клетки; различают эластическое (обратимое) и пластическое (необратимое) растяжение клетки; прекращение роста клетки обусловлено увеличением толщины оболочки и уменьшением скорости обмена веществ к концу фазы растяжения. Д. Мэзия в 1963 г. опубликовал важную аналитическую работу по теории митоза и физиологии клеточного деления при росте растений [46]. Д. Мэзия, характеризуя физиологические особенности деления клетки, отмечает следующее: процессы в митотическом аппарате клетки не функционируют автономно, они протекают синхронно во многих (но не во всех) ядерных (многоядерных) клетках. Синхронность митотических и эндомито-тических циклов определяется специальными митотическими центрами; во время деления расхождение сестринских хромосом в начале анафазы происходит одновременно; в конце митоза вокруг хромосом появляется оболочка, и они переходят в интерфазное состояние; движение отдельных хромосом к экватору хорошо координируется между собой ([46], стр. 332). Объясняя механизм «удвоения клеток», Д. Мэзия [46] отмечает, что нормальный цикл репродукции клетки включает удвоение всех функциональных потенций: каждая из двух дочерних клеток способна делать все, что способна делать родительская клетка, включая удвоение потенциала роста, соответствующего максимуму «рабочей массы», максимальному размеру и мак- симальной скорости роста. Когда клетка приступает к делению, она неспособна к дальнейшему росту, но через некоторое время способность к росту восстанавливается: две дочерние клетки имеют суммарную скорость роста в два раза больше, чем скорость роста родительской клетки на той же стадии; две дочерние клетки производят в два раза больше клеточного вещества, чем материнская клетка ([46], стр. 357), а безъядерные фрагменты вообще не растут. Ю.К. Росс в 1966 г. опубликовал важную теоретическую работу [47], в которой для описания роста растения используется система обыкновенных дифференциальных уравнений первого порядка вида:

Pij =- в, Z Pij = 0, i, j=1

dm                     ^{4           4}

~7T = k F ^Ф j ^- k R R j ^- V j + Z ( A j ^- A ji ) + Z ( B j ^- B ji )

d ^T                                     i = 1                   i = 1

(уравнение (2), стр. 481, [47]), где кғ, kR - коэффициенты пропорциональности соответственно при фотосинтезе и дыхании;

Ф j , R j - интенсивность соответственно фотосинтеза и дыхания j -го органа растения;

V j - скорость отпада мертвых частей j -го органа растения; A y , By - скорость оттока соответственно «свежих» и «старых» ассимилятов из i -го органа в j -й орган растения;

( A ij - A ji ), ( B y - B ji ) - скорость обмена соответственно «свежих» и «старых» ас-симилятов между i- м и j- м органами растений; M = Z т^ - сухая масса органов растения;

j = 1 соответствует листьям, j = 2 соответствует стеблю растения;

j = 3 соответствует корням;

j = 4 соответствует репродуктивным органам растения.

Предполагается, что выполняются приближенные условия:

• л, = к „ф, а , B , - в„ = в м ij F i ij ij ji ij

(уравнения (3), стр. 481, [47]), где а у - коэффициент, определяющий долю созданных на единицу времени в i -ом органе растения «свежих» ассимилятов, оттекаемых в j -й орган, причем выполняется условие «нормировки»:

Z ^a у = 1, i , j = 1

P i/ - коэффициент пропорциональности, определяющий долю скорости оттока «старых» ассимилятов из i -го органа в j -й орган, если p _Zj > 0, и долю скорости притока , если p _Zj < 0, отнесенной к единице сухой биомассы целого растения ( М), причем выполняются условия:

P ij =- P ji ,   Z P ij = 0.

• i ,    j = 1

Совокупность значений a ij определяет матрицу вегетативного роста , которая имеет 12 независимых составляющих и по физиологическому смыслу она отражает закон распределения «свежих» ас-симилятов по отдельным органам растения, созданных в процессе фотосинтеза. Совокупность значений Р і/ определяет матрицу репродуктивного роста , она имеет шесть независимых составляющих и по физиологическому смыслу отражает закон перераспределения по отдельным органам растения «старых», уже созданных ассимилятов ([47], стр. 482). Работы Ю.К. Росса [47; 48] имели и имеют большое теоретическое и практическое значения. Г.М. Добрынин в 1969 г. опубликовал большую фундаментальную работу [49], посвященную исследованию продуктивности хлебных и кормовых злаков. Характеризуя особенности роста и формирования злака в разных фазах развития растений, в книге [49] он отмечает важную роль меристемы - главной образовательной ткани растений: одно из основных свойств меристематических клеток - их способность делиться и обра-87

зовывать ткани растений; источником образования новых тканей у злаков при выходе в трубку является верхушечная система , а в основаниях каждого междоузлия соломины до фазы цветения развивается промежуточная (интеркалярная) меристема ; узел кущения начинает формироваться в фазе всходов, а рост главного стебля не прекращается во время кущения . На рисунке 7 показано схематическое изображение роста и формирования главного побега овса посевного в течение вегетации 1958 г. (рис. 76, стр. 106, [49]).

трубку стебля, а затем фаза выметывания. В период образования соцветия стебель продолжает расти и развиваться, увеличивая длину и вверх до определенной (максимальной) высоты : подъем соцветия внутри трубки из влагалищ листьев происходит в результате удлинения меж-доузлиевых растений в процессе промежуточного (интеркалярного) роста стебля. На рисунке 8 показана принципиальная схема роста стебля и соцветия (метелки) главного побега овса посевного в течение вегетации 1958 г. (рис. 77, стр. 107, [49]).

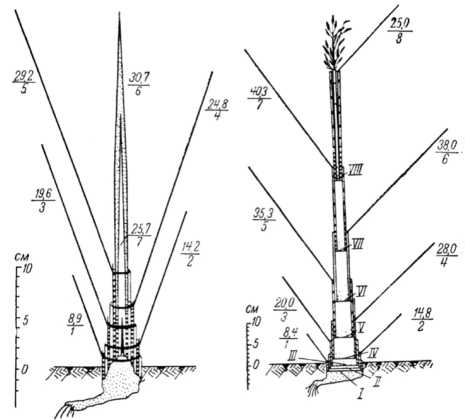
Рисунок 7 – Схематичное изображение роста и формирования главного побега овса посевного в течение вегетации 1958 г. [49] Слева – в фазе выхода в трубку (24 июня), справа – в фазе выметывания (18 июля).

Цифра в числителе – длина (в см) пластинки листа;

в знаменателе – порядковый номер листа; I–VIII – узлы стебля

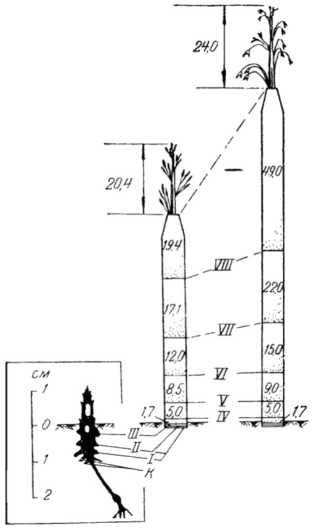
Рисунок 8 – Динамика роста стебля и соцветия (метелки) главного побега овса посевного в течение вегетации 1958 г. Слева – в фазе выхода в трубку, в продольном разрезе (на обеих сторонах видны остатки удаленных листьев и корней, а на верхушке – зачаток метелки длиной 0,2 см; длина стебля над поверхностью почвы 1 см), в центре – в фазе выметывания, справа – в фазе цветения, к – коле-оптильные корни узла кущения: I–VIII – порядковые номера узлов стебля. Цифрами обозначена длина междоузлий стебля (в см) ([49], рис. 77)

Опытами установлено [49], что главный стебель ярового овса после всходов находился в укороченном состоянии и конус нарастания располагался ниже поверхности почвы , побег формировался из вегетативных органов; после образования всех листьев верхушечная меристема конуса нарастания способствовала образованию основных генеративных органов растения и начиналась фаза выхода в 88

Основные элементы именно этой расчетной схемы роста стебля являются наиболее полными на современном этапе развития учения о злаках в разных условиях, и используются в дальнейшем. В.В. Кузьмичев в 1977 г. отмечает, что « число конкретных уравнений роста, предложенных в разное время исследователями, давно уже перевалило за сотню и увеличивается с каждым годом » ([50], стр. 43). Математический анализ значительного количества их проведен в книге В. Пешеля (W. Peschel. Die mathema-tischen Methoden zur Herleitung der Wachstumgezetze von Baum und Bestand und die Ergebnisse ihrer Anwendung. – Berlin, 1938, st. 169–248). В своей монографии [50] Кузьмичев В.В., в частности, отмечает следующие математические модели роста деревьев как функция времени:

• - формула Теразаки (1915 г.):

_ _ I b i y = a expI — | к x)

(формула (2.11), стр. 46, [50]), где а, b – постоянные коэффициенты, определяемые по фактическим данным роста (у) растения методом наименьших квадратов;

• х – возраст растения;

  - формула Леваковича (Lewacowic, 1935 г.):

a y = ~r—іл

li b i c I 1 1 I

к   x)

(формула (2.1), стр. 44, [50]), где а , b , c – постоянные коэффициенты, определяемые по фактическим данным роста ( у ) растения;

• х – возраст растения;

  - формула Корсуня (Korsun, 1935 г.):

y = a exp(b In x + c ln2 x)

(формула (2.3), стр. 44, [50]);

- формула Хугерсхофа (Hugershoff, 1936 г.):

y' = ax2 exp(- cx)

(формула (2.4), стр. 44, [50]), где у ' - скорость роста растения (производная первого порядка от функции роста ( у ) растения);

• -    формула Коллера (которую приводит W. Peschel):

y = axb exp(- cx)

(формула (2.16), стр. 48, [50]);

• -    формула Митчерлиха (Mitscherlich, 1919 г.):

y = y max ⁽ 1 — e ^- cx ^{) 2}

(формула (2.5), стр. 44, [50]) и т. д.

В книге [50] специально отмечается, что « действительных законов роста растения еще не найдено » ([50], стр. 44); различные формулы роста растений, предложенные для прогноза текущего прироста и применяемые для составления таблиц хода роста, пригодны только для коротких периодов времени , поэтому в расчетах часто используют значения относительного роста . Например, для математической модели роста Коллера относительная скорость роста растения определяется по формуле:

y ' b — = — c yx

(формула (2.18), стр. 48, [50]).

Для математической модели роста Теразаки относительная скорость роста растения определяется по формуле:

У-=b-

У x2

(формула (2.12), стр. 48, [50]) и т. д.

На рисунках 9, 10 показаны фактические (точки) и расчетные кривые хода роста деревьев по разным математическим моделям роста растений (рис. 2, стр. 47, [50]).

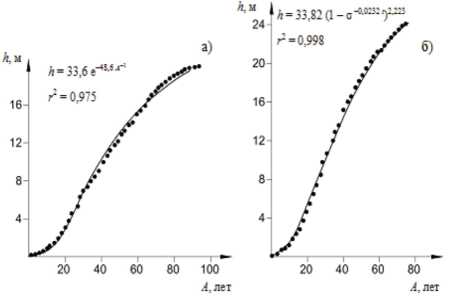
Рисунок 9 - Динамика роста дерева в высоту ( а ) с использованием функции Теразаки и по диаметру ( б ) с использованием уравнений Келлера и Корсуня (рис. 2, стр. 47, [50])

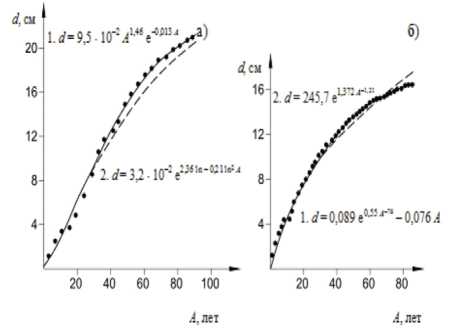
Рисунок 10 - Динамика роста дерева в высоту ( а ) с использованием уравнения

Митчерлиха и по диаметру ( б) с использованием формул Шимека и Корфа (рис. 2, стр. 47, [50])

Из графиков на рисунках 9, 10 видно хорошее соответствие фактических и рас-90

четных значений разных характеристик хода роста деревьев по математическим моделям роста разных авторов. В.В. Галицкий, А.С. Комаров в 1979 г. опубликовали важную теоретическую работу [51], в которой весь комплекс факторов, влияющих на рост растения разделен на две группы: зависящие от жизнедеятельности растений ( a i , a 2 , а з , — .a k ) и независящие от жизнедеятельности растений ( P i , Р 2 , Р з , — Р m ); принадлежность конкретного фактора определяется конкретными условиями, характером почвы, типом растения и т. д. Скорость роста биомассы растения при этом определяется обыкновенным дифференциальным уравнением первого порядка:

dB ,₊

— = ж с

dT

^—

с-

(уравнение (1), стр. 715, [51]), где ж - параметр, определяемый по сле- дующим соотношениям:

[ A(T)        ,   A (T

, если 1 >       >  0,

A(T)          Aj(T)

ж = ]

1          A ( T

1, если        >  1,

Aj(T)

где A y ( T) = A j ( T ) - функция возраста растения, определяющая количество средств существования органа j -го типа, необходимое для свободного роста растения;

B j ( T) - скорость роста биомассы свободно растущего растения возраста Т ;

С ⁺ - положительная составляющая средств существования A ( T ), приходящихся на растение к общему количеству средств существования A j ( T );

С ^- - отрицательная составляющая средств существования A ( T ), приходящихся на растение к общему количеству средств существования A j ( T ).

Авторы статьи [51] специально отмечают, что исследование вопросов о величинах и взаимосвязи параметров, влияющих на динамику изменения биомассы растений в разных условиях, представляет большой практический интерес и должно проводиться как методами моделирования, так и экспериментальным путем. Вопрос о том, какую долю полной массы конкретного растения составляет биомасса, о способе отнесения отдельных фракций массы конкретного растения к биомассе, т. е. к массе, в которой идет значительный обмен веществ в настоящее время, видимо, не ясен. Представляется, что решение его нужно искать на пути моделирования динамики клеточной структуры растительной массы и соответствующей экспериментальной идентификации моделей ([51], стр. 721). В 1979 г. опубликована важная теоретическая работа Р.В. Янко, В.М. Янко [52], в которой проведена систематизация и классификация основных математических моделей роста растений и установлено, что наиболее общей моделью роста является математическая модель на основе классического обыкновенного дифференциального уравнения Бернулли ([52], стр. 41-42), таблица 2.

В статье [52] отмечается, что в качестве основного показателя при математическом описании процессов развития растений наиболее приемлемым является относительный или логарифмический прирост в функции роста:

(уравнение (1), стр. 644, [52]), где х - функция роста (абсолютный рост растения;

f(x ) - эмпирическая зависимость относительного прироста растения вида:

f (x ) = a- rx

(формула (2), стр. 644, [52]), где a, r - постоянные коэффициенты, определяемые по фактическим значениям относительного роста растения.

Для собственных вегетационных опытов с кукурузой сорта Буковинская 3 в течение 1970-1979 гг., когда в сосуды Вагнера с дерново-подзолистой почвой вносилось: аммиачная селитра - 1 г, однозамещенный фосфат натрия - 0,5 г, сульфат калия - 1 г, известь - 12 г на один сосуд при влажности почвы 60-70 % от полной влагоемкости, а высота растений измерялась через равные интервалы времени при 30-кратной повторности опытов для трех растений, получены сле- дующие соотношения:

f 1 )— = 0,108 - 68.10-5 x, у x J At

1)— = 0,085 - 83.10-5 x,

У x J At

f 1)— = 0,101 - 73,5 -10-5 x

у x J At

(формулы (19), (20), (21), стр. 647, [52]), и соответствующие уравнения для абсо лютного роста трех растений кукурузы:

^{x ( t} ) =

^{x ( t} ) =

0,108

117 • 10-4 exp(- 0,108t)+ 68 • 10-5

0,085

320 • 10-4 exp(- 0,085t)+83 • 10-5

^{x ( t} ) =

0,101406 • 10-4 exp(- 0,101t)+73,5 • 10-5

(формулы (22), (23), (24), стр. 647, [52]).

1 ^ dx _ d (ln x) x J dt     dt

= f ^{( x} )

Таблица 2

Классификация уравнений роста растений [52]

Автор уравнения	Уравнение роста, приведенное к определенному виду	Значение функции P ( t ), Q ( t ) и коэффициента n	Уравнение роста в интегральной форме
Уравнения с разделенными или разделяющимися переменными (однородные) dx + р(Дх _ q dt
Горячкин	dx - Bat - a — 1 x = 0 dt	P ( t ) = - Bat" a - 1	- Bt ~a x = ce
Келлер и Гутенберг, Пэрл, Майнер и Паркер	dx  (a   ^   _ --1-- r 1 x = 0 dt  V t    )	P ( t ) = -(a- r 1 V t    )	x = ct a e ~rt
Милтроп	d "°g x ' -a + 2 rt = 0 dt	P ( t ) = -a + 2 rt	log x = a t - rt 2 + c
Линейные уравнения первого порядка с правой частью (неоднородные) dy + p)t^x _ g(f) dt
Шмальгаузен, Джемс Бейли	dx --+ kx = a k dt	P ( t ) = k , Q ( t ) = a k	x = a ( 1 - ce kt )
Гомпертс, Куртис	d (ln x )     ,           ,   , —---- - a ln x = -a ln A dt	P ( t ) = -a, Q ( t ) = -a ln A	a t x = A • e ce
Шинозаки, Кира	dx --a x = -aA dt	P ( t ) = -a , Q ( t ) = -a A	x = ce a t + A
Уравнения типа Бернулли dx + р ( t ) x = Qtx n
Берталанфи	dx   a      a A 1   „ — +-- x =---- x m dt 1 - m     1 - m	P ( t ) -      , n = m , Q ( t ) - i 1 - m            1 - m	1 x = ( ce "a t + A1" m ) 1 - m
Робертсон, Ферхюльст, Гартман, Раденауэр	dx           2 --a x = - rx dt	P ( t ) = -a, n = 2, Q ( t ) = - r	a x =------;---- -a t c a e  + r
Пэрл	dx          s=^, s — = a x = - x J kt dt        J	P ( t ) = -a, n = 2, Q ( t ) = J ksts s = 0	1 x =--------------- n------ -a t ,    -a t ( a t       sS ce   + e   | e J kst dt
С. Де. Витт	dx        a 7 --a x = — x dt         A	P ( t ) = -a , n = 2, Q ( t ) = -!	A x =------;--- cAe "a t -1

Авторы статьи [52] предлагают процесс роста растения на протяжении всего вегетационного периода рассматривать состоящим из трех фаз :

Xt),  при tо < ti < te,

x (t )=1 f (t),

пРи te < ti < tn ,

^(t),  при tn < ti < tk

(соотношения (4), стр. 644, [52]), где ф(t) - начальная фаза роста растения; f(t) - основная фаза роста;

ф ( t ) - конечная фаза роста растения.

На рисунке 11 показаны эмпирические (точки) и теоретические кривые абсолютного роста растений, соответствующие последним уравнениям; сравнение опытных и расчетных значений показывает хорошее соответствие результатов: отклонения составляют 1,0-7,0 %, 2,0-5,0 %, 3,0-3,5 %.

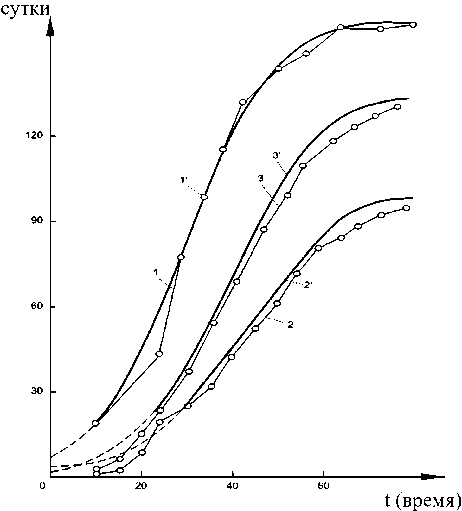
Рисунок 11 ^- Фактические (точки) и расчетные кривые (сплошные линии) абсолютного роста ⁽ х ) трех растений кукурузы в функции времени ⁽ t ):

1 , 2 , 3 - опытные значения;

1 ', 2 ', 3' - расчетные значения [52]

По мнению авторов статьи [52], полученные закономерности объективно отражают процесс роста растений в основной фазе ^([52], стр. 64⁸⁾ В статье [52] для сравнения результатов проведены расчеты на основе решения известного дифференциального уравнения Ферхюльста:

А

x (t ) =--------+ C

i + ioa-rt

(уравнение (28), стр. 648, [52]), где А ^- асимптота роста растения;

С - постоянный коэффициент, определяющий значение роста растения для времени t = ^0:

x ^{( t} ) =

177,6

1 + Ю1,205 - 0,0361 ¹

+ 0,6

(уравнение (29), стр. 648, [52]).

Средняя относительная ошибка между опытными и расчетными значениями при использовании уравнения Ферхюльста 7 %, что в пять раз больше, чем по предложенной математической модели.

В 1966-1983 гг. важный цикл теоретической работы выполнили сотрудники Института математики Сибирского отделения АН СССР [55-59]. В статье И.А. Полетаева [55], во-первых , определены наиболее общие положения составления математических моделей биогеоценозов (БГЦ). Во-вторых , установлены основные этапы построения математических моделей БГЦ. Наконец , в статье [55] приведены общие и строгие классификационные признаки составления математических моделей БГЦ, согласно которым должны удовлетворять математические модели: существенным для моделирования является то, что некоторые признаки объекта R не совпадают с признаками его модели; полное совпадение всех признаков (до совпадения расположения во времени и пространстве) есть просто тождество объекта R с самим собой. Для одного и того же объекта R может быть найдено или построено несколько различных моделей М 1 , М 2 , М з , ... Две различные модели М 1 и М 2 одного и того же объекта R могут отличаться друг от друга по различным совокупностям признаков; это дает основание для классификации моделей.

• 1)    Пусть А есть множество всех признаков объекта R, доступных наблюдению и находящихся в поле нашего внимания; а есть отдельный признак, а е А. Рассмотрим подмножество A i с A признаков, объявленных нами «существенными». Предположим, что для модели М 1 это подмножество есть А 1 , а для модели М 2 - А 2 . Тогда A 1 и А 2 суть совокупности признаков, сохраняемых или «отображаемых» соответственно в моде-

• ли M1 и М2. Если имеет место строгое включение A1 с А2 (А i есть собственное подмножество множества А2), т. е. каждый признак аj1, сохраняемый в M1, сохраняется также и в М2, но не наоборот, то М2 называется «широкой» моделью по сравнению с M1, a M1 «узкой» по сравнению с М2.

• 2)    Расчленим объект R на некоторое число частей, которые структурно и функционально связаны между собой. Пусть модель М 1 отображает только признаки объекта R в целом, и пусть модель М 2 , кроме этого, может быть расчленена на части таким образом, что некоторые части модели М 2 будут моделями частей объекта R. В таком случае модель М 2 называется «сильной» моделью R по сравнению с М 1 , а М 1 «слабой» моделью по сравнению с М 2 .

• 3)    Модель М объекта R обладает, кроме множества признаков A i , общих для М и R, некоторым множеством «собственных» признаков В М , не принадлежащих совокупности признаков объекта А. Множество признаков В М называется « реализацией » модели М. Различные модели М 1 , М 2 , … одного объекта R могут различаться своей реализацией. Различия отдельных реализаций В М 1 , В М 2 сводятся не только к различиям вещественной природы моделей (модель-машина, модель-животное, модель-система уравнений), но и к различиям в способах кодирования, т. е. сопоставления частей, состояний, изменений, имеющих место соответственно в объекте R и модели M j .

По совокупности признаков реализации все модели естественно разбиваются на два класса: модели реальные и модели знаковые. Реальная модель MR объекта R по природе своей физической реализации необходимо обладает признаками, отмеченными как «существенные» в объекте R. Знаковые модели Ms суть условные описания объекта R в некотором алфавите символов, операциях над символами и некотором коде. В качестве примера приложения общих положений построения математических моделей БГЦ в статье [55] получена математическая модель свободного роста растений, на основе следующих гипотез: растение в процессе роста сохраняет геометрическое подобие; свободную энергию и активное вещество растение получает только посредством фотосинтеза; свободная энергия расходуется, кроме расходов, связанных с протеканием процесса фотосинтеза, на построение живой ткани (рост) и на подъем раствора из почвы; в среднем, за большие отрезки времени, растение получает постоянное количество света на единицу поверхности и может поглощать необходимые питательные вещества из неограниченного запаса ([55], стр. 175– 176). При оговоренных условиях в статье [55] получено уравнение свободного роста растения в виде:

dx

— = a - bx

dt

(уравнение (1), стр. 176, [55]), где х – высота растения;

а, b – постоянные коэффициенты, учитывающие приход и расход энергии на увеличение массы растения.

Решение основного уравнения роста представляется в виде:

x (t) = a^th[Tab (t -10)]

(соотношение (2), стр. 176, [55]).

На рисунке 12 показаны результаты расчетов (сплошная линия) и фактические данные (точки) высоты дуба в зависимости от времени (возраста) по результатам опытов А.А. Молчанова (А.А. Молчанов. Научные основы ведения хозяйства в дубравах лесостепи. – М.: Наука, 1964).

И.А. Полетаев отмечает [55], что для взрослого растения (от 40 до 220 лет) совпадение расчетной и экспериментальных кривых оказалось хорошим, однако полученное совпадение кривых не является доказательством справедливости сделанных выше предложений, но свидетельствует весьма сильно в пользу их правдоподобия; дальнейшему развитию результатов работы [55] посвящены исследования Т.И. Эман [56], Ю.И. Гиль-дермана [57] и Г.П. Карева [58; 59].

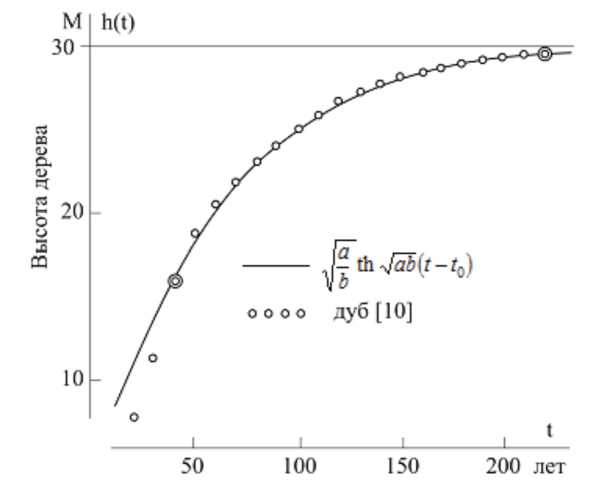
Рисунок 12 – Зависимость высоты растения ( h ) от возраста ( t ) при свободном росте ([55], рис. 1)

В статье Г.П. Карева [59], в частности, впервые учитывается конкуренция растений за величину полученной энергии при фотосинтезе, что определяется интенсивностью суммарной солнечной радиации внутри растительного покрова на определенной высоте и значением суммарной площади листьев в слое от верхней границы растительного полога на единицу поверхности почвы. Дифференциальное уравнение роста растений с учетом густоты насаждений при этом имеет вид:

dH = -^2 1 - exp (- pH2 )]-bH2 dt pH

(уравнение (9), стр. 476, [59]), где Н – высота растений;

• а , b , р – постоянные коэффициенты;

р – коэффициент, учитывающий густоту растений [59].

Результаты расчетов на ЭВМ позволили получить следующие данные [59]. В таблице 3 приведены фактические и расчетные значения высоты дубового древостоя по данным А.А. Молчанова, которые использовались в статье И.А. Полетаева [55].

Таблица 3

Рост дубового древостоя (Молчанов, 1964, табл. 64)

Возраст	Высота		Отклонение, %
	табличная	расчетная
10	3,1	3,1	0
20	7,7	7,95	3,21
30	12,3	12,11	–1,56
40	16,0	15,51	–3,063
50	18,7	18,24	–2,48
60	20,4	20,41	0,05
70	21,8	22,15	1,58
80	23,0	23,54	2,34
90	23,9	24,66	3,18
100	24,9	25,57	2,68
110	25,8	26,3	1,94
120	26,6	26,89	0,36
130	27,3	27,38	0,29
140	27,7	27,77	0,27
150	28,1	28,09	–0,015
160	28,4	28,36	–0,15
170	28,7	28,57	–0,44
180	28,9	28,75	–0,53
190	29,1	28,89	–0,72
200	29,3	29,0	–1,0
210	29,4	29,1	–1,0
220	29,5	29,18	–1,08

Из данных таблицы 3 видно, что максимальное отклонение +3,21 %, среднее – +0,176 %, среднеквадратичное – 2,8 %. По причинам технического характера при расчетах в качестве единицы длины были взяты 10 м, единицы времени – год. В этих единицах значения параметров а , b , р , для которых приведены расчеты таблицы 3, равны: а = 0,052; b = 0,00181; р = 0,36.

В таблице 4 приведены фактические и расчетные значения высоты сосновых насаждений по данным Ф.П. Михневича (Ф.П. Михневич. Ход роста сосновых насаждений БССР. – Минск, 1962).

Из данных таблицы 4 следует, что максимальное отклонение +2,33 %, среднее – +0,9 %, среднеквадратичное – 1,97 %. Значения параметров: а = 0,05736, b = 0,004473. Для таблицы хода роста сосняка бонитета I максимальное отклонение со- ставляет +3,385 %, среднее – +0,3 %, среднеквадратичное – 2,4 % при а = 0,04775, b = 0,0048.

Таблица 4

Рост сосновых насаждений. Бонитет I а (Михневич, 1962)

Возраст	Высота		Отклонение, %
	табличная	расчетная
20	10,3	10,3	0
30	15,0	15,29	1,93
40	19,2	19,65	2,33
50	23,0	23,3	1,32
60	26,0	26,28	1,07
70	28,4	28,63	0,8
80	30,3	30,45	0,5
90	31,8	31,84	0,12
100	33,0	32,88	–0,36
110	34,0	33,66	–1,01
120	34,8	34,23	–1,63
130	35,3	34,65	–1,84
140	35,8	34,97	–2,33

Для таблицы хода роста сосняка бонитета II максимальное отклонение равно 3,85 %, среднее – -0,33 %, среднеквадратичное – 2,7 % при а = 0,0395, b = 0,00522. Таким образом, бонитет насаждения связан с величиной параметра а . В таблице 5 приведены фактические и расчетные значения хода роста сосновых насаждений по данным авторов работы [60].

Таблица 5

Ход роста густых сосновых насаждений (Рубцов, 1976)

Возраст	Численность (на 1 га)	Высота		Отклонение, %
		табличная	расчетная
15	7700	4,8	4,8	0
20	5975	7,3	7,1	–2,74
25	4950	9,3	9,11	–2,034
30	3960	10,8	10,85	0,444
35	3200	12,1	12,35	2,054
40	2680	13,3	13,65	2,645
45	2260	14,4	14,79	2,73
50	1925	15,4	15,8	2,59
55	1675	16,3	16,69	2,42
60	1464	17,2	17,5	1,72
65	1315	18,0	18,22	1,21
70	1188	18,7	18,87	0,91
75	1093	19,4	19,46	0,33
80	1019	19,9	20,0	0,54

Из данных таблицы 5 видно, что при росте редких насаждений максимальное отклонение -3,37 %, среднее – +0,26 %, среднеквадратичное – 2 % при а = 0,052, b = 0,0018, р = 0,5. Для таблицы хода ро-96

ста очень редких насаждений максимальное отклонение равнялось -4,2 %, среднее – -0,26 %, среднеквадратичное – 2,65 % при а = 0,059, b = 0,0021, р = 0,489. Работы [55–59] имели и имеют важное фундаментальное теоретическое значение для теории роста растений; вероятно. Впервые в работе [59] получена математическая модель роста растений с учетом густоты насаждений, что позволяет исследовать ряд важных практических задач оптимизации выращивания разных сельскохозяйственных культур.

Новая приближенная цифровая модель роста и продуктивности сельскохозяйственных растений. В отличие от уже известных моделей роста и развития растений ниже предлагается цифровая модель роста и продуктивности сельскохозяйственных культур на основе главных положений и результатов клеточной теории строения и роста растений: детальное описание механизмов деления клеток (ядер) растений при росте дано в фундаментальных работах Л. Иоста [61], К. Сент-Илера [62], В.Ф. Раздорского [63], Ф.Р. Уайта [64], С.О. Гребинского [45], Д. Мэзия [46], К. Эсау [65], П. Данжара [66], А. Фрей-Висслинга [67], Л. Гельбруна [68], Д.М. Гродзинского [69] и других. В частности, воспользуемся результатами работ Р.О. Эриксона (R.O. Erickson, 1951–1959) с сотрудниками [70–73] и В.Б. Иванова [74–77], в которых экспериментально и теоретически исследованы многие вопросы роста и размножения клеток разных растений (особенно корневой системы). Опытами установлено, что растущая часть корня состоит из двух зон – меристемы и зоны растяжения; в меристеме длина клеток мало меняется с удалением от кончика корня, и с началом растяжения удаление клеток прекращается, а за зоной растяжения образуются корневые волоски. Клетки в меристеме объединены в продольные ряды, которые возникают иногда от одной инициальной клетки, которая может делиться в разных направлениях; посте- пенно всякая клетка удаляется от конца корня за счет деления и роста и на определенном расстоянии деление клеток прекращается. Число клеток в одном продольном ряду до остановки деления можно приближенно найти по формуле:

N = 2 j ^{+ 1} - 1.        (1)

Число клеток в последнем потомстве при этом равно:

П j max ^ ,

где j – число делений после отделения от инициальной клетки.

Из формул (1) и (2) следует, что увеличение числа делений (j) на единицу приводит к удвоению числа клеток в меристеме и к удвоению числа клеток, выходящих из меристемы, что не соответствует экспериментальным данным. Опытами установлено, что значение числа делений для зерновых не превышает 6– 7 и, таким образом, рост корня растения начинается при наличии хотя бы одной «живой клетки», когда N^ = 1 (ү = 0) и продолжается до значений Nm * 64 -128, когда ү = 6-7 [70; 71; 78]. Причем частота делений клетки является разной в разных частях клеток водит

меристемы и возможно деление в разных направлениях, что при-к разветвлению рядов, которые удаляются от конца корня приближенно до середины меристемы. Опытами установлено, что клетка в меристеме делится ограниченное количество раз в течение небольшого времени, за исключением инициальных клеток, поэтому в растущей части корня происходит постоянная смена клеток. Расстояния между границами растущих клеток всегда увеличиваются, и поэтому положение клетки определяется временем и расстоянием от инициальной клетки ряда. Опытами установлено, что клетки разных тканей, расположенные на одном расстоянии от конца корня, удаляются с одинаковой скоростью. Чтобы исследовать скорость роста расте- ния воспользуемся основными положениями дифференциального уравнения [79]. Пусть в момент времени t = t1 растение имело длину S = S1, а в момент времени t = t2 растение имело длину S = S2. Прирост длины растения AS = S2 - Si разделим на приращение времени роста At = 12 -11 и получим среднюю скорость роста растения:

иср ( t )=£.         (3)

При неравномерном росте растения средняя скорость u_cp ( t ) неудовлетворительно определяет скорость роста растения , поэтому используют предел отношения f A S при A t >  0, т. е.:

(a t )

u ( t ) = lim — = d⁵ ,      (4)

At >0' At    dt который называют «скоростью роста» (u(t)) (формула (2), стр. 280, [72]; формула (2), стр. 488,  [71]; формула (2.1), стр. 13,  [78]. Формула (4) определяет производную первого порядка для непрерывной функции S(t), которая характеризует изменение высоты растения во времени (или длины корня).

В.Б. Иванов [78] скорость роста клетки корня растения определяет соотношением:

A^

u(t ) = lim — = — at >0 A tdt

(соотношение (2.1), стр. 13, [78]), где AI - прирост длины клетки за время At.

Скорость роста апикального отрезка корня определяется отношением:

V ( t ) = lim ^{A L} = dL        (6)

a t > 0 A t   dt

(соотношение (2.2), стр. 13, [78]), где AL - прирост апикального сегмента корня растения за время A t .

Если длина корня апикального отрезка корня равна длине растущей части корня, 97

то скорость V ( t ) равна скорости роста всего корня V _s( t ):

V_K (t ) = lim ^A L ^K = dL^    (7)

a t > 0 A t     dt

(соотношение (2.3), стр. 13, [78]), где V к - скорость роста всего корня растения в момент времени t ;

AL к - прирост длины корня растения за время A t.

Прирост длины корня, или прирост длины клетки, определяют за относительно большие промежутки времени ( A t ), но чем меньше значение A t , тем ближе измеренные значения роста и ( t ) и V ( t ), однако при слишком малых значениях A t возрастают ошибки измерений ([78], стр. 1314). Чтобы повысить точность изучения изменений скорости роста клеток в работах Р.О. Эриксона [71; 72] и В.Б. Иванова [76; 78] предложено использовать значение относительной скорости роста клеток ( k ):

( 1 ) d £ V £ J dt

(формула (3), стр. 488, [71]; формула (2.7), стр. 14, [78]), где I - длина клетки в момент времени t.

Допускается, что значение коэффициента k является постоянным , для средней длины клетки ( I ) с номером N из соотношения (8) получают экспоненциальный закон роста длины клетки:

£ = £ ₀ e kt

(соотношение (2.30), стр. 34, 46 [78]), где I о - средняя длина клетки в начале участка.

Относительная скорость роста апикального отрезка корня ( К) определяется отношением:

K =[ 1 ] dL          (9)

V L J dt

(соотношение (2.11), стр. 15 [78]), где L - длина апикального отрезка корня. 98

Принимая значение коэффициента К постоянным, утверждается [78], что расстояние от кончика корня ( L ) растет по экспоненциальному закону:

L = L ₀e ^Kt

(соотношение (2.40),стр. 47 [78]), где L 0 – длина расстояния от кончика корня для клетки, которая образовалась после митоза и имеет длину ℓ 0 .

Однако ранее экспериментальными исследованиями В.Б. Иванова (1965) установлено, что при постоянном значении коэффициента К клетки метаксилемы корня не делятся (стр. 34, [78]), и, таким образом, имеется противоречие между результатами опытов и теории .

Относительная скорость образования клеток ( ү ) определяется отношением:

Ү =

¹ 1 dn n J dt

(формула (2.14), стр. 16 [78]).

Формула (10) показывает сколько клеток возникает за единицу времени из одной клетки (часто значение коэффициента ү выражается в процентах, и тогда формула (10) показывает на сколько процентов увеличилось число клеток ( n ) за единицу времени) (стр. 15, [78]).

Допуская, что значение коэффициента ү является постоянным , для среднего числа образовавшихся клеток ( n ) из соотношения (10) получают экспоненциальный закон размножения клеток :

n = n eY' ⁰

где n 0 – среднее число клеток в начале митоза.

Значение относи т ельной скорости образования клеток ( ү ) используется для определения митотического индекса (МИ) растен и я:

МИ = ү.т             ⁽¹¹⁾

(соотношение (2.16), стр. 16 [78]), где т - продолжительность митоза.

Соотношения (8)–(11) являются основными в клеточной теории роста растений [71–78]. Результаты опытного изучения размножения клеток на протяжении меристемы позволяют ее рассматривать как экспоненциально растущую популяцию клеток . Действительно, в потомстве клетки после выхода ее из покоящегося центра деления идут через равные промежутки времени и практически все клетки делятся . Различия между ними проявляются только во время последнего митоза. Таким образом, на протяжении меристемы число клеток растет по экспоненциальному закону. Это подтверждается при анализе данных о соотношении τ и МИ для меристем разных корней (стр. 65, [78]). Можно отметить одну важную общую особенность формул (8), (9) и (10): соотношение (8) не определяет значение коэффициента k при ℓ → 0, и поэтому при этих условиях формула (8) не определяет относительную скорость роста клеток корня растения ; соотношение (9) не определяет значение коэффициента K при L → 0, и поэтому при этих условиях формула (9) не определяет относительную скорость роста апикального отрезка корня ; соотношение (10) не определяет значение коэффициента γ при n → 0, и поэтому при этих условиях формула (10) не определяет относительную скорость образования клеток ( при n → 0 нет клеток и нет деления ).

Указанные выше недостатки моделей роста на основе формул (8), (9) и (10), во-первых, доказаны результатами опытов N. Sanderland, R. Brow (1956, Journ. Exper. Bot., vol. 7, № 19) и N. Sanderland (1960, Journ. Exper. Bot., vol. 11, № 31): на рисунке 13 показаны кривые роста сырой массы (1) пятого листа люпина, числа клеток (2) в нем, и его длины (3) и площади (4) согласно опытным данным N. Sanderland (рис. 50, стр. 184, [78]). Из кривых (1), (2), (3) и (4) на рисунке 13 видно, что ни одна из них не выходит из точки (0;0) начала координат; специально отмечается точка а выхода листа из почки и точка б, где в опытах установлено прекращение делений клеток и т. д. Во- вторых, недостатки моделей роста на основе уравнений (8), (9) и (10) не позволили Р.О. Эриксону, К.Б. Сакс (Proc. Amer. Philos. Soc., 1956, vol. 100, pp. 499–514) получить опытные значения относительной скорости роста корня семян кукурузы (Zea mays) при малых значениях времени (t ≈ 0); рост фиксировался фотокамерой от момента появления первых корней до роста длиной около 8 см; за начало отсчета длины корня принималось значение 10 мм от кончика; всего было 25 зерен, которые предварительно замачивали в дистиллированной воде в течение 24 ч; опытная (сплошная линия) и расчетная (пунктирная линия) кривые изменения скорости роста корня (метки от кончика корня) кукурузы из работы Р.О. Эриксона, К.Б. Сакс [71] показаны на рисунке 14.

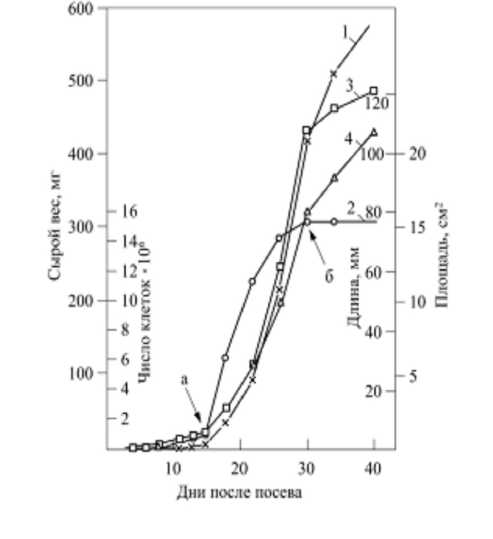
Рисунок 13 – Кривые роста сырого веса листа ( 1 ), числа клеток в нем ( 2 ), его длины ( 3 ) и площади ( 4 ); пятый лист люпина (N. Sanderland, 1960):

стрелкой а обозначен выход листа из почек, а стрелкой б – прекращение деления

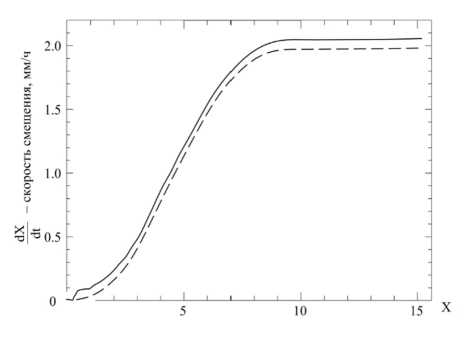
Рисунок 14 – Скорость смещения меток от кончика корня кукурузы; опытная (сплошная линия) и расчетная (пунктирная линия) (рис. 5, стр. 494, [71])

В таблице 6 приведены опытные и расчетные данные роста корня кукурузы (перемещение от кончика корня ( Х ), скорость роста Г dX A и относительная ско-

I ^dt )

ро^сть роста Г1 Y dX ) корня кукурузы) на . X Л dt )

основе 10 фотографических записей [71].

Таблица 6

Изменения роста в длину первичного корня кукурузы ( Zea mays ) на основе 10 фотографических записей [71]

Расстояние от кончика корня Х , мм	Средняя скорость смещения, мм/час	95% -ный интервал изменения	dX dt		Г 1 A dX 1 X ) dt
			опыт, мм/час	расчет, мм/час	опыт, 1/час	расчет, 1/час
1	2	3	4	5	6	7
0 , 00	– 2 , 042	±0, 097	0 , 000	0 , 000	0 , 047	0 , 000
0 , 25	– 2 , 044	±0, 119	– 0 , 002	0 , 001	0 , 127	0 , 012
0 , 50	– 1 , 968	±0, 102	0 , 074	0 , 006	0 , 132	0 , 026
0 , 75	– 1 , 957	±0, 092	0 , 085	0 , 014	0 , 099	0 , 041
1 , 00	– 1 , 952	±0, 087	0 , 090	0 , 027	0 , 048	0 , 066
1 , 25	– 1 , 917	±0, 082	0 , 125	0 , 047	0 , 104	0 , 093
1 , 50	– 1 , 896	±0, 078	0 , 146	0 , 074	0 , 131	0 , 124
1 , 75	– 1 , 857	±0, 076	0 , 185	0 , 110	0 , 161	0 , 148
2 , 00	– 1 , 815	±0, 073	0 , 227	0 , 154	0 , 188	0 , 181
2 , 25	– 1 , 758	±0, 072	0 , 284	0 , 202	0 , 209	0 , 212
2 , 50	– 1 , 715	±0, 082	0 , 327	0 , 258	0 , 232	0 , 258
2 , 75	– 1 , 642	±0, 088	0 , 400	0 , 321	0 , 265	0 , 291
3 , 00	– 1 , 576	±0, 088	0 , 466	0 , 396	0 , 328	0 , 323
3 , 25	– 1 , 488	±0, 089	0 , 554	0 , 483	0 , 371	0 , 347
3 , 50	– 1 , 385	±0, 095	0 , 657	0 , 581	0 , 409	0 , 366
3 , 75	– 1 , 286	±0, 092	0 , 756	0 , 679	0 , 397	0 , 379
4 , 00	– 1 , 189	±0, 094	0 , 853	0 , 775	0 , 359	0 , 384
4 , 25	– 1 , 102	±0, 094	0 , 940	0 , 865	0 , 354	0 , 380
4 , 50	– 1 , 020	±0, 096	1 , 022	0 , 955	0 , 348	0 , 370
4 , 75	– 0 , 920	±0, 092	1 , 122	1 , 044	0 , 376	0 , 361
5 , 00	– 0 , 838	±0, 093	1 , 204	1 , 136	0 , 371	0 , 352
5 , 25	– 0 , 733	±0, 089	1 , 309	1 , 224	0 , 340	0 , 344

Продолжение таблицы 6
1	2	3	4	5	6	7
5 , 50	– 0 , 662	±0, 087	1 , 380	1 , 310	0 , 331	0 , 332
5 , 75	– 0 , 581	±0, 085	1 , 461	1 , 391	0 , 315	0 , 317
6 , 00	– 0 , 496	±0, 079	1 , 546	1 , 468	0 , 309	0 , 299
6 , 25	– 0 , 425	±0, 075	1 , 617	1 , 540	0 , 276	0 , 277
6 , 50	– 0 , 364	±0, 069	1 , 678	1 , 607	0 , 242	0 , 255
6 , 75	– 0 , 300	±0, 059	1 , 742	1 , 666	0 , 232	0 , 235
7 , 00	– 0 , 249	±0, 055	1 , 793	1 , 722	0 , 217	0 , 212
7 , 25	– 0 , 193	±0, 045	1 , 849	1 , 772	0 , 192	0 , 188
7 , 50	– 0 , 150	±0, 038	1 , 892	1 , 817	0 , 168	0 , 162
7 , 75	– 0 , 112	±0, 031	1 , 930	1 , 855	0 , 137	0 , 139
8 , 00	– 0 , 081	±0, 026	1 , 961	1 , 887	0 , 113	0 , 114
8 , 25	– 0 , 055	±0, 018	1 , 987	1 , 912	0 , 085	0 , 088
8 , 50	– 0 , 038	±0, 015	2 , 004	1 , 931	0 , 066	0 , 065
8 , 75	– 0 , 024	±0, 009	2 , 018	1 , 945	0 , 047	0 , 045
9 , 00	– 0 , 012	±0, 006	2 , 030	1 , 954	0 , 030	0 , 030
9 , 25	– 0 , 009	±0, 005	2 , 033	1 , 959	0 , 014	0 , 018
9 , 50	– 0 , 006	±0, 004	2 , 036	1 , 962	0 , 004	0 , 010
9 , 75	– 0 , 005	±0, 004	2 , 037	1 , 963	0 , 003	0 , 004
10 , 00	– 0 , 005	±0, 003	2 , 037	1 , 964	0 , 002	0 , 001
10 , 25	– 0 , 004	±0, 003	2 , 038	1 , 964	0 , 003	0 , 000
10 , 50	– 0 , 003	±0, 003	2 , 039	1 , 965	0 , 002	0 , 000
10 , 75	– 0 , 003	±0, 003	2 , 039	1 , 965	0 , 000	0 , 000
11 , 00	– 0 , 003	±0, 003	2 , 039	1 , 965	0 , 000	0 , 000

При математической обработке опытных данных (средние значения смещения, значения скоростей роста и т. д) авторы статьи [71] использовали стандартные методы численного интегрирования (или дифференцирования) на основе известной формулы Симпсона [79]. Специально отмечается, что « это правило (формула) при численном интегрировании нельзя применять для t = 0, поэтому за начало счета было принято время, когда длина от кончика корня была равна 10 мм » ([71], стр. 496). Можно отметить, что применяемая методика обработки опытных данных в статьях Р.О. Эриксона с соавторами [70–73] является приближенной, поэтому результаты этих работ нуждаются в уточнении и развитии. Например, опытное значение относительной скорости роста корня на расстоянии 0,5 мм от кончика корня равно 0,132 (1/час), а расчетное значение при этом равно 0,026 (1/час), т. е. в 5 раз меньше. Важно, что опытные значения относительной скорости роста корня кукурузы показывают наличие интервалов увеличения и уменьшения на определенных периодах (Сакс, Сабинин, Хаксли, Иванов и др.), а расчетные значения в работе [71] не имеют таких интервалов , поэтому модели роста Р.О. Эриксона [70–

• 73] и В.Б. Иванова [78] нуждаются в уточнении и дальнейшем развитии.

Важную аналитическую работу по изучению механизма роста растительных клеток опубликовали в 1955 г. Р. Броун, В. Рейт, Е. Робинсон [80]. Авторы статьи [80] специально отмечают, что современные исследования показали, что увеличение размера клеток связано с увеличением многих компонентов системы, и поэтому вместо термина «растяжение клеток» предлагается использовать термин «рост клеток» ([80], стр. 407), и процесс роста клетки включает все изменения, в результате которых меристематическая клетка превращается в зрелую вакуолизированную клетку. На рисунке 15 показано изменение объема клеток в корне гороха, в частности, при их превращении из меристематических клеток в полностью вакуолизированные клетки (опыты R. Brown, D. Broadbent, 1950) ([80], стр. 409, рис. 1).

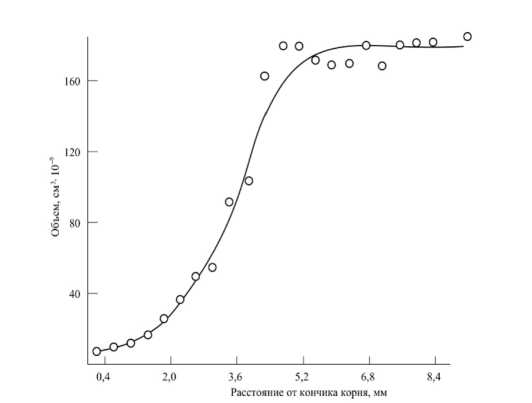
Рисунок 15 – Средний объем клеток (определяемый путем пересчета на одну клетку) корня гороха, расположенных на разном расстоянии от его кончика (стр. 409, рис. 1, [80])

Результаты опытов (рис. 15) показывают, что для того, чтобы проходил рост корня гороха, необходимо наличие определенного объема клеток из меристематической системы растения; при отсутствии меристематических клеток не будет происходить рост корня. Результаты многих опытов показывают, что в пе- риод роста непрерывно совершаются изменения в клетке, которые, достигнув определенного критического значения (уровня), понижают скорость различных процессов обмена и рост клетки прекращается. Рост клетки можно определить через его скорость на единицу количества конкретного фермента, или комплекса ферментов, или в единицах абсолютного или относительного уменьшения общего количества комплекса в течение роста. Опытами установлено, что метаболизм клеток при увеличении размеров изменяется: например, измерения роста фрагментов корня бобов длиной 1 мм в растворе сахарозы в течение 24 часов показали, что способность к росту этих фрагментов корня разная: чем больше расстояние от участка, где взят фрагмент корня, до кончика корня, тем больше способность клеток к росту, усиление роста клеток корня наблюдается до расстояния около 3 мм, а затем рост уменьшается, рисунок 16.

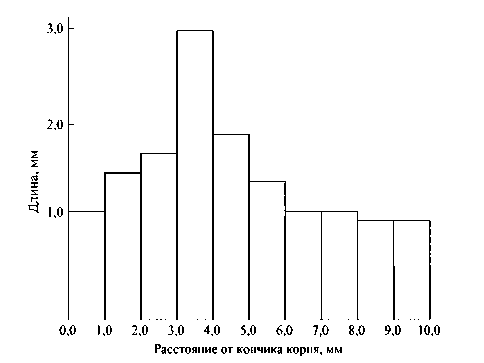
Рисунок 16 – Длина последовательных 1-миллиметровых фрагментов корешка бобовых после культивирования в течение 24 час в 2%-ном растворе сахарозы (рис. 6, стр. 417, [80])

Из данных рисунка 16 видно, что для того, чтобы проходил рост корня гороха, необходимо наличие определенной длины фрагмента корешка; без фрагмента корня деление клеток не будет происходить и, следовательно, не будет происходить рост корня. Эксперименты, выполненные в Кембридже (Cambridge) под руководством профессора А. Фрей-Вис-слинга [81], позволили установить, что рост клеточной оболочки проходит две стадии: рост клеток колеоптиля путем растяжения представляет собой биполярный верхушечный рост; растущая клеточная оболочка является живой структурой, пропитанной цитоплазмой, которая (in situ) синтезирует микрофибриллы; в делящихся клетках микрофибриллы наклоняются к клеточной пластинке, к которой они прикреплены, и поэтому рост клеточной оболочки представляет автономный процесс, обуславливающийся формообразующей способностью живого протопласта ([81], стр. 406).

Вместо соотношений (8), (9) и (10) для описания изменения относительных скоростей длины клетки ( ℓ ), длины апикального отрезка ( L ) и количества размножения клеток ( n ) предлагается использовать соответственно следующие дифференциальные уравнения:

л

d £

—

I £ min + ^ J dt

max

f    1    1 dL (13) 1Lmin + L J dt = M (L max L ), dn

f 1    1

I n min ⁺ n J

dt

max

- П ),

где m , M , Г – постоянные коэффициенты, которые можно назвать соответственно «коэффициент роста длины клеток» ( m ), « коэффициент роста длины апикального отрезка корня » ( М ) и « коэффициент роста количества клеток » (Г);

ℓ max , L max , n max – постоянные параметры, определяющие максимальную длину клетки ( ℓ max ), максимальную длину апикального участка ( L max ) и максимальное количество клеток ( n max ). Значения ℓ max , L max , n max определяются по опытным (фактическим) данным для определенных растений и конкретных почвенноклиматических условий;

ℓ min – начальная (минимальная) длина клетки, она не равна нулю ( I min * 0), потому что при ℓ min = 0 нет клетки ;

L min – начальное (минимальное) расстояние от кончика корня, оно не равно нулю ( L min * 0), потому ЧТО при L min = 0 нет корня ;

n min – начальное (минимальное) количество клеток, при которых начинается процесс деления, поэтому значение n min не равно нулю ( n min * 0), потому что при n min = 0 нет клетки и нечему делиться; значения параметров ℓ min , L min , n min определяются по опытным данным.

Для решений уравнений (12), (13), (14) можно назначить начальные условия:

ℓ ( t 0 ) = ℓ 0 ,    L ( t 0 ) = L 0 ,    n ( t 0 ) = n 0 ,   (15)

ℓ 0 , L 0 , n 0 , t 0 – постоянные, определяющие длину клетки ( ℓ 0 ), длину апикального участка ( L 0 ) и число клеток ( n 0 ) для « начального значения времени » ( t 0 ).

Соотношения (12)–(14) позволяют сделать следующую физиологическую интерпретацию:

• -    уравнение (12): относительная длина клетки ( ℓ ) и относительный прирост этой длины пропорциональны разности между максимальной длиной ( ℓ max ) и фактическим значением длины ( ℓ );

• -    уравнение (13): относительная длина апикального участка корня ( L ) и относительный прирост этой длины пропорциональны разности между максимальной длиной ( L max ) и фактическим значением длины ( L );

• -    уравнение (14): относительное количество клеток растения ( n ) и относитель-

ный прирост этого количества клеток пропорциональны разности между максимальным числом клеток ( n max ) и фактическим количеством клеток ( n ). Отметим, что уравнения (12)–(14) имеют подобную структуру и отличаются только значениями постоянных коэффициентов. Для высоты ( Н ) или массы ( М ), или наружного диаметра ( D ) и урожайности ( у ) растения можно записать подобные (аналогичные) уравнения:

У ( t ) =

У max ⁽ У min ⁺ У 0 ^{) e}xP ^[ n ( У max ⁺ У min )( t ^— t 0 ^{)] —} У min ( У max

⁽ У min ⁺ У 0 ^{) e}xP ^[ n ⁽ У max ⁺ У min )( t ^— t 0 ^{)] + (} У max ^— У 0 )

Z 2 L^ (23)

Значение постоянного коэффициента ( n ) можно найти по формуле:

n = Һ[ ⁽ У max ^— У 0 )( У min ⁺ У ^{)] — ln [(} У min ⁺ У 0 )( У max 2) ] . (24)

⁽ У max ⁺ У mm )( t ^— t 0 )

Значение постоянного коэффициента ( y max ) можно найти по формуле:

Г i 1

к

H „in + H ) dt

— = k (H

max ^{— H} )

y max

^{+ У} min =

^{2 (} У 1 ⁺ У min Х у 2 ⁺ У min X У 3 ⁺ У min ) ^— ( У 2 ⁺ У min ^ ( У 1 ⁺ У 3 ^{+ 2} У min ' ⁽ У 1 ⁺ У min )( У 3 ⁺ У min ^{) — (} У 2 ⁺ У min ^{) 2}

и «начальное» условие вида:

Н(t0) = Н0, k, Hmin, Hmax, H0, t0 – постоянные;

Г 1     1

к y min

+ У ) dt

dy = n ( У

max

—

где y 1 , y 2 , y 3 – фактические значения урожайности ( у ), полученные через равные интервалы фактора роста ( t ), т. е. t 3 – t 2 = t 2 – t 1 , и, соответственно, y 1 = y ( t 1 ), y 2 = y ( t 2 ), y 3 = y ( t 3 ).

и «начальное» условие вида:

у ( t 0 ) = у 0 ,                             (19)

n , y min , y max , y 0 , t 0 – постоянные ( t – фактор роста [38; 43]).

Решение уравнения (16), удовлетворяющее начальным условиям (17), можно

Изложенная выше методика позволяет определить приближенную цифровую модель, когда действует несколько факторов. Например, в случае совместного действия света (И), минерального питания (П) и дыхания (Д) на рост растения ( Н ) можно записать следующую систему четырех уравнений:

записать в виде:

H ( t ) =

H max ( H min + H 0 ) exp [ k ( H m„ + H i )( t — 1 0 ) ] — H „„ ( H „„ — H 0 ) ^.(20) ( H min + H 0 ) exp [ k ( H max + H m„ )( t — t 0 ) ] + ( H „„ — H 0 )

Г---1---^ — = n (Hmax — H ) ИПД, к Hmn + H) dt      max        M

Значение постоянного коэффициента ( k ) можно найти по формуле:

k = ln [( H m„ — H 0Қ H mn + H )] — ln [( H mn + H „Қ H max — H )] ^{. (21) (} H max ⁺ H min X t ^— t 0 )

Значение постоянного коэффициента ( H max ) можно найти по формуле:

^H max ^{+ H} min

= 2 ( H 1 + H min X H 2 + H min X H 3 + H _ ) - ( H ₂ + H . . ) 2 ( H 1 + H 3 + 2 H min )

( H 1 + H min X H 3 + H min ) — ( H 2 + H min ) 2              ’ (22)

где H 1 , H 2 , H 3 – фактические значения высоты растения ( Н ), полученные через равные интервалы изменения времени, т. е. t 3 – t 2 = t 2 – t 1 , и, соответственно, Н 1 = Н ( t 1 ), Н 2 = Н ( t 2 ), Н 3 = Н ( t 3 ).

Для (продуктивности) урожайности ( у ) на основе уравнений (18) и (19) можно получить соотношения:

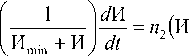
— И ) РПД,

Г 1   ) d n

I        I—= n

I ⁿ min ⁺ П ) ^dt

— П ) РИД,

^Г /   1 ^dy = n 4 ( Д- — Д ) ^РИП,

_к Дшіп + Д ) dt где n1, n2, …, Дmin, Дmax – постоянные параметры, определяемые по фактическим данным.

Для решений уравнений (26) можно назначить начальные условия:

Н ( t 0 ) = Н 0 , И( t 0 ) = И 0 , П( t 0 ) = П 0 , Д( t 0 ) = Д 0 , (27)

t 0 , H 0 , И 0 , … – постоянные.

Система уравнений (26) является нелинейной и допускает численное решение. Общий анализ влияния разных факторов (интенсивность света, интенсивность питания, интенсивность дыхания) на рост (и продуктивность) растений можно проводить по следующим соотношениям:

^H min ^ln

H min + H H min + H 0

n i || H min + H max 1 И +И

2 У\ min     max /

^H min ^ln

n ₁

n ₂

^{+ H} max ln

Иmin ln

H - + H

H min + H 0

^H min ^{+ H} max

^Дшіп ^{+ Д}max

^H min ^ln

H max

- H

H max - H 0

И і + И

^Иmin ⁺ И 0

+ H mJ'1

Дmin ln

H min + H H min + H 0

nL || ^H min ^{+ H} max n 2 /\ ^Пшіп ^{+ n}max

^{+ И} x¹'

И max

- И

^Иmax ^- И 0

H

max

- H

H max — H 0

■ l m. + Д

Д шіп + Д 0

^{+ H} max ІП

Пmin ln

⁺ Д™1п

H max

^H max

- H

H 0

Д max

Д max

-

Д

-

Д 0 . ’

II n + П

П шіп + П

^{+ n}max ln

П max П max

- П

П 0

Примеры использования новой цифровой модели. Пример 1. Используем результаты экспериментов при исследовании влияния азотистых и фосфорнокислых удобрений на урожай хлопчатника в условиях вегетационного опыта. Условия и технология проведения опытов описаны подробно в статье Д.А. Сабинина с соавторами [25], а результаты экспериментов приведены выше в таблице 1; используем опытные значения урожайности:

у 0 = 23,57; у 1 = 23,57; у 2 = 61,53; у 3 = 77,67

по формуле (25) находим значение максимально возможного урожая:

2 ( 23,57 + 23,57 )( 23,57 + 61,53 )( 23,57 + 77,67 ) - ( 85,14 ) 2 ( 148,38 )

y max ⁺ y ^mi n =                      ( 47,14 )( 101,24 ) - ( 85,14 ) 2

,

Таблица 7

Опытные и расчетные значения урожайности хлопчатника

№№ п./п.	Доза азота х i	Урожайность (опыт) у i	Коэффициент действия n i	Урожайность (расчет) у ( х i )	Скорость роста у ' ( х)
1	0,75	23,57	–	23,570	–
2	1,50	36,21	0,006009	36,210	16,665
3	2,25	50,99	0,007591	48,123	17,894
4	3,00	61,53	0,006753	62,634	12,112
5	6,00	77,67	0,005103	79,630	2,549

Из данных таблицы 7 видно хорошее соответствие опытных и расчетных значений урожайности хлопчатника: максимальное относительное отклонение составляет 5,6 % для дозы фосфора 2,25 (г/сосуд); по формуле Митчерлиха максимальное относительное отклонение составляет при этом 8,5 % (табл. 1). Из данных таблицы 7 видно, как изменяется скорость роста урожайности хлопчатника: до значения дозы азота 2,25 (г/сосуд) скорость роста урожайности увеличивается, а после этого значения дозы азота скорость роста урожайности уменьшается при увеличении дозы азота; подобным образом изменяется « коэффициент действия фактора роста » ( n i ).

Пример 2. Воспользуемся экспериментальными результатами роста дубового древостоя (А.А. Молчанов, 1964), которые использовали И.А. Полетаев [55] и Г.П. Карев [59], таблица 3, согласно которой принимаем значения: Н 0 = H min = 3,1; t 0 = 10; H max = 29,55. По формулам (20) и (21) проведены расчеты, которые приведены в таблице 8.

или:

у max + 23,57 = 106,174, или:

у max = 82,604.

По формуле (24) для каждого опытного изменения дозы азота находим значения « коэффициента действия фактора роста » ( n i ) и по формуле (23) определяем возможное (прогнозное) значение урожайности ( у i ) хлопчатника, таблица 7.

Таблица 8

Опытные и расчетные значения высоты дубового древостоя

№№ п./п.	Возраст t i , годы	Высота (опыт) Н i , м	Коэффициент действия фактора k i	Высота (расчет) H ( t i ), м	Скорость роста H ( t i ), м/год
1	2	3	4	5	6
1	10	3,1	–	3,1	–
2	20	7,7	0,002284	7,7	0,539
3	30	12,3	0,001810	13,56	0,481
4	40	16	0,001398	17,05	0,362
5	50	18,7	0,001085	19,42	0,256
6	60	20,4	0,000751	21,10	0,161
7	70	21,8	0,000685	21,92	0,132
8	80	23	0,000659	23,04	0,112
9	90	23,9	0,000556	24,05	0,084
10	100	24,9	0,000707	24,69	0,092

Продолжение таблицы 8
1	2	3	4	5	6
11	110	25 , 8	0 , 000755	25 , 74	0 , 081
12	120	26 , 6	0 , 000818	26 , 54	0 , 071
13	130	27 , 3	0 , 000900	27 , 24	0 , 061
14	140	27 , 7	0 , 000639	27 , 84	0 , 036
15	150	28 , 1	0 , 000785	28 , 03	0 , 035
16	160	28 , 4	0 , 000739	28 , 41	0 , 026
17	170	28 , 7	0 , 000954	28 , 63	0 , 025
18	180	28 , 9	0 , 000840	28 , 92	0 , 017
19	190	29 , 1	0 , 001145	29 , 05	0 , 016
20	200	29 , 3	0 , 00181	29 , 23	0 , 014
21	210	29 , 4	0 , 001573	29 , 41	0 , 007
22	220	29 , 5	0 , 003374	29 , 46	0 , 005

Из данных таблицы 8 видно хорошее соответствие опытных и расчетных значений высоты дубовых деревьев; также данные таблицы 8 показывают, что скорость роста деревьев Н ′ ( t i ) неравномерно уменьшается после возраста деревьев в 10 лет практически до нуля к 220 годам.

Пример 3. Воспользуемся экспериментальными результатами роста сосновых насаждений (Ф.П. Михневич, 1962), которые использовал Г.П. Карев [59], таблица 4, согласно которой принимаем значения: Н 0 = H min = 10,3; t 0 = 20; H max = 36,05. По формулам (20) и (21) проведены расчеты, которые приведены в таблице 9.

Таблица 9

Опытные и расчетные значения высоты сосновых насаждений

№№ п. / п.	Возраст t i , годы	Высота (опыт) Н i , м	Коэффициент действия фактора k i	Высота (расчет) H ( t i ), м	Скорость роста H ′ ( t i ) , м/год
1	20	10 , 3	–	10 , 3	–
2	30	15 , 0	0 , 000878	15 , 0	0 , 467
3	40	19 , 2	0 , 000811	19 , 53	0 , 403
4	50	23 , 0	0 , 000812	22 , 99	0 , 353
5	60	26 , 0	0 , 000749	26 , 22	0 , 273
6	70	28 , 4	0 , 000726	28 , 46	0 , 215
7	80	30 , 3	0 , 000719	30 , 31	0 , 167
8	90	31 , 8	0 , 000730	31 , 78	0 , 130
9	100	33 , 0	0 , 000776	32 , 93	0 , 102
10	110	34 , 0	0 , 000906	33 , 87	0 , 082
11	120	34 , 8	0 , 00110	34 , 68	0 , 062
12	130	35 , 3	0 , 001125	35 , 29	0 , 038
13	140	35 , 8	0 , 002393	35 , 60	0 , 027

Данные таблицы 9 показывают хорошее соответствие опытных и расчетных значений высоты сосновых насаждений.

Пример 4. Воспользуемся экспериментальными результатами роста сосновых насаждений (В.И. Рубцов, 1976), которые использовал Г.П. Карев [59] при исследовании влияния густоты насаждений на рост, таблица 5, согласно которой принимаем значения: Н 0 = H min = 4,8; t 0 = 15;

H max = 20,15. По формулам (20) и (21) проведены расчеты, которые приведены в таблице 10 .

Таблица 10

Опытные и расчетные значения высоты густых сосновых насаждений

№№ п. / п.	Возраст t i , годы	Высота (опыт) Н i , м	Коэффициент действия фактора k i	Высота (расчет) H ( t i ), м	Скорость роста H ′ ( t i ) , м/год
1	15	4 , 8		4 , 80
2	20	7 , 3	0 , 003280	7 , 30	0 , 510
3	25	9 , 3	0 , 002582	9 , 83	0 , 395
4	30	10 , 8	0 , 002003	11 , 21	0 , 292
5	35	12 , 1	0 , 001841	12 , 20	0 , 250
6	40	13 , 3	0 , 001843	13 , 29	0 , 228
7	45	14 , 4	0 , 001876	14 , 38	0 , 207
8	50	15 , 4	0 , 001938	15 , 37	0 , 185
9	55	16 , 3	0 , 002033	16 , 26	0 , 165
10	60	17 , 2	0 , 002469	17 , 05	0 , 160
11	65	18	0 , 002822	17 , 91	0 , 138
12	70	18 , 7	0 , 003399	18 , 59	0 , 115
13	75	19 , 4	0 , 005519	19 , 18	0 , 100
14	80	19 , 9	0 , 008970	19 , 76	0 , 055

Данные таблицы 10 показывают хорошее соответствие опытных и расчетных значений высоты сосновых насаждений при разной густоте.

Пример 5. Воспользуемся фактическими данными о густоте насаждений (В.И. Рубцов, 1976), которые использовал Г.П. Карев [59], таблица 5, согласно которой принимаем значения: N 0 = N min = 7700; x 0 = 15; N max = 982. Расчеты по формулам (20) и (21) приведены в таблице 11 .

Таблица 1 1

Фактические и расчетные значения численности деревьев на площади 1 га

№ № п / п	Возраст x i , год	Число деревьев на 1 га (факт) N i , шт.	Коэффициент действия факторов роста k i	Число деревьев на 1 га (расчет) N ( x i ), шт.	Скорость изменения густоты, шт./год
1	15	7700	–	7700	–
2	20	5975	4,09941Е- 06	5975	– 279 , 9047592
3	25	4950	3,49833Е- 06	4802 , 8274	– 175 , 5994939
4	30	3960	4,73433Е- 06	4184 , 70009	– 164 , 3923776
5	35	3200	5,23485Е- 06	3261 , 5102	– 126 , 5586776
6	40	2680	5,02817Е- 06	2661 , 89959	– 88 , 62271513
7	45	2260	5,59435Е- 06	2296 , 61501	– 71 , 20986621
8	50	1925	6,21452Е- 06	1953 , 61117	– 56 , 40528212
9	55	1675	6,48973Е- 06	1684 , 00224	– 42 , 16293404
10	60	1464	7,83972Е- 06	1494 , 80904	– 34 , 62840252
11	65	1315	8,14118Е- 06	1319 , 55704	– 24 , 43978804
12	70	1188	1,07367Е- 05	1213 , 22234	– 19 , 6580559
13	75	1093	1,39968Е- 05	1110 , 12381	– 13 , 66117124
14	80	1019	2,51131Е- 05	1042 , 10696	– 8 , 101570464

Данные таблицы 11 показывают хорошее соответствие фактических и расчетных значений числа деревьев на площади 1 га.

Заключение. В качестве основных выводов по работе можно отметить следующие положения.

• 1.    Представлен краткий обзор и анализ существующих математических моделей расчета роста и продуктивности сельскохозяйственных растений.

• 2.    Предложена новая приближенная цифровая модель роста растений и урожайности (продуктивности) на основе главных положений и результатов клеточной теории строения и роста растений.

• 3.    Приведены примеры расчетов, показывающие хорошее соответствие фактических и расчетных значений высоты растений, урожайности сельскохозяйственных культур при разных климатических и почвенных условиях.