Применение цепей Маркова при прогнозировании динамики скорости ветра

Now more and more attention in many fields о Г scientific researches is given to modelling various processes and systems. The reason is mostly the large progress in computing engineering and information science that gave the possibility to realize very- difficult correlations and to pass the computing with high accuracy. Today the wide used practice is the preliminary test of the devices and operation modes at the mathematical model tliat reflects the main correlations inside the device and between the device and the environment. The modern modelling of the technical part of the wind power plant is dcpclopcd very deeply. One of the reason of it is the very high level of the determination of the some system elements behavior that causes in determinate model. The Markov's cliain is applicable to be used for the description of the mathematical model of the wind speed variation because it gives the possibility to join probabilistic nature of the wind and the determinism of its distribution. The Markov's cliains could be adapted and automated and allow to compute not only the dynamics probability of a particular wind speed, but also to determine automatically the possibility of the transfer operating modes appearance of the wind power plant. The join of the researches of the wind power plants at the preliminary- determined speeds and the dynamics of the wind speed for the determination of the extreme modes with the researches using Markov's chains allows to pass fuller researches of the yvind power plant. The Markov's cliain allows to determine the possibility of the occurcncc of some yvind modes (which arc characterised not only the speed of the yvind but also the dynamics of one) and to determine the possibility of the yvind modes which could be dangerous for the wind power plant. Combination of wind turbines researches al a predetermined yvind speed and the dynamics of their cliangcs in order to determine the limit operating conditions of wind turbines with tests using Markov cliains allows a more complete study of yvind turbines. Markov chains allow to set the occurrence probability of certain wind conditions (characterized not only by the wind flow speed, and by the dynamics of its changes) and to establish the occurrence probability of wind modes tliat can be dangerous for the device.

Kev words: Markov's chain, yvind. yvind flow. model, mathematical, modeling.

Введение. В настоящее время всё большее внимание во многих областях научных исследований уделяется моделированию различных процессов и систем. Причиной тому в значительной степени является огромный прогресс в вычислительной технике и информатике, что позволяет реализовывать достаточно сложные взаимосвязи и проводить расчёты на их основе с большой скоростью. Всё это позволяет проводить расчёты с применением моделей высокой сложности и получать очень близкие к практическим результатам данные.

В математике накоплен огромный аппарат, пригодный для проведения моделирования очень сложных процессов и систем, который длительное время почти не использовался в практике моделирования из-за трудностей, связанных с большим количеством расчётов.

Подобные трудности преодолевались различными путями, и некоторые, весьма сложные модели были реализованы с применением сравнительно простых физических явлений.

Одним из первых аналоговых вычислительных машин является антикитерский механизм, созданный в 150-100 гг. до н.э. Эта вычислительная машина служила для моделирования движения небесных тел: Солнца, Луны, Меркурия, Венеры, Марса, Юпитера и Сатурна [1]. Далее следуют та кие устройства, как логарифмическая линейка, планиметр и интеграторы Крылова и Лукьянова [2].

Лукьянов заинтересовался причинами образования трещин в бетоне. Его предположение об их температурном происхождении сталкивается со скептическим отношением специалистов. Молодой инженер начинает исследования температурных режимов в бетонных кладках в зависимости от состава бетона, используемого цемента, технологии проведения работ и внешних условий. Распределение тепловых потоков описывается сложными соотношениями между температурой и меняющимися со временем свойствами бетона. Эти соотношения выражаются так называемыми уравнениями в частных производных. Однако существовавшие в то время (1928 год) методы расчетов не смогли дать быстрого и точного их решения.

Лукьянов сумел обобщить идеи великих ученых: модель — вот высшая степень наглядности математической истины. Проведя исследования и убедившись, что законы течения воды и распространения тепла во многом сходны, он сделал вывод — вода может выступать в роли модели теплового процесса. В 1934 году Лукьянов предложил принципиально новый способ механизации расчетов неустановившихся процессов — метод гидравлических аналогий и спустя год создал тепловую гидромодель для демонстрации метода. Это примитивное устройство, сделанное из кровельного железа, жести и стеклянных трубок, успешно разрешило задачу исследования температурных режимов бетона.

В 1936 году заработала первая в мире вычислительная машина для решения уравнений в частных производных - гидравлический интегратор Лукьянова [3].

Аналоговые вычислительные машины в настоящее время применяются там, где требуется высокая скорость вычислений. Иногда утверждают, что цифровые вычисления с применением математических моделей обладают ограниченной точностью, но уже разработаны программные средства, позволяющие производить вычисления с числом знаков после запятой, ограниченным только объёмом доступной памяти машины [4].

Таким образом, моделирование и модель как высшая степень наглядности являются очень важными составляющими научных исследований. В модели можно «заглянуть» внутрь интересующих процессов и систем без необходимости привлечения сложных механизмов измерений, которые, к тому же, могут вносить значимые погрешности в результаты.

В настоящее время широко распространённой практикой является предварительное испытание устройств и режимов их работы на математических моделях, отражающих существенные взаимосвязи внутри устройства и с внешней средой. После получения результатов моделирования становится возможным внести корректировки в конструкцию, что позволяет исключить изготовление первого экспериментального образца, который выявит эти же проблемы в устройстве.

В области конструирования достаточно больших машин и аппаратов математическое моделирование является «почти» обязательным из-за значительных затрат ресурсов на изготовление каждого образца, особенно если разрабатываемая машина будет выпущена достаточно небольшой серией.

Нельзя переоценить и важность математического моделирования для эконо- мики, поскольку в этом случае возможна экономия ресурсов на изготовление первого экспериментального образца, который выявляет наибольшее число недостатков в конструкции. Часто выявление некоторых из этих недостатков приводит не только к изменениям в конструкции, но и значительным изменениям во всём процессе производства устройства, что оказывает ещё большее влияние на цену не только выпуска аппарата, но и на цену проведения научных исследований.

В математическом моделировании существуют как детерминированные, так и стохастические модели. И если с детерминированными моделями достаточно успешно работают, то стохастические модели в значительно большей степени являются хорошо разработанным разделом математики, в меньшей мере находящим своё применение в прикладной практике.

В настоящее время всё большее применение может находить такой статистический раздел математики, как теория цепей Маркова. Этот раздел является частью теории вероятностей и потому пригоден для стохастического моделирования.

Целью работы является обоснование возможности применения теории цепей Маркова для создания стохастической модели динамики скорости ветра.

Описание метода и его обсуждение. Цепь Маркова с дискретным временем описывает систему, которая изменяет своё состояние в дискретные моменты времени, согласуясь с некоторым случайным механизмом. При этом задаются вероятности переходов из текущего состояния системы во все остальные возможные состояния системы [5, 6].

Так, если пронумеровать состояния системы номерами 1, 2, 3, 4, то матрица вероятностей переходов, например, примет следующий вид:

1/3 1/3 1/3^ 1/4 1/4 1/4 1/4 1/2 1/2 0 0 <0 0 0 1 ) а соответствующий ей рисунок, отражающий переходы (без указания переходов, приводящих к сохранению состояния, то есть находящихся на главной диагонали матрицы), примет вид, приведённый на рисунке.

Применение цепей Маркова позволяет проводить математическое моделирование в тех областях, которые ранее считались «мертвыми». Одной из таких областей является бурно развивающаяся в настоящее время ветроэнергетика, в том числе малая ветроэнергетика [7], для которой значение таких математических моделей выше.

На сегодняшний день моделирование технической части ветроустановок разработано в достаточной мере. Одной из причин этого служит очень высокий уровень определённости поведения отдельных элементов системы, что приводит к детерме-нированной модели. Варианты таких моделей для ветроустановок приводятся в [8-10], однако в них рассмотрены только вопросы моделирования ветроустановки, а входным параметром модели хоть и выступает скорость ветра, она принимается фиксированной или изменяющейся по известному закону.

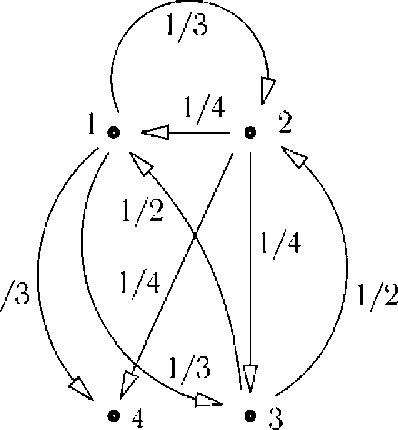
Переходы в цепи Маркова

Таким образом, цепь Маркова является пригодной для использования при описании математической модели изменения скорости ветра, поскольку она содержит вероятности перехода к другим скоростям ветра, то есть вероятности снижения или усиления ветра, а кроме этого ещё и ускорение ветра, если рассматривается фиксированное время.

Цепи Маркова работают с дискретным количеством состояний системы, что требует разделения диапазона «возможных» скоростей ветра на интервалы. Под «возможными» скоростями ветра следует понимать диапазон скоростей ветра, которые со сколь-нибудь значимой вероятностью. Этот интервал обязательно начинается от 0 и заканчивается скоростью ветра 20 или 25 м/с, поскольку вероятность появления скоростей ветра выше этих пределов крайне мала. Интервал разбиения следует выбрать 2 или 1 м/с.

Интервал дискретных шагов времени также следует выбрать достаточно небольшим, 0,5 или 1 с. Следует отметить, что слишком малые интервалы времени потребуют для точного прогнозирования построения цепи Маркова достаточно большой длины, а объём данных цепи Маркова возрастает в степени длины цепи, поэтому построение цепи Маркова длиной более 5-7 звеньев потребует значительных объёмов экспериментальных данных и приведёт к образованию достаточно большой матрицы вероятностей.

Поясним приведённое. Если заданы диапазоны скоростей ветра в качестве состояний системы и заданы вероятности перехода к другим скоростям ветра, то если переход осуществляется в состояние со скоростью ветра, непосредственно примыкающей к текущему, то ускорение равно отношению шага разбиения скоростей ветра к единичному интервалу времени. Если же переход осуществляется в состояние со скоростью ветра, отстоящей от текущего на одно состояние (или через одно), то ускорение будет больше в два раза и так далее.

Если номера состояний соответствуют скоростям ветра 1, 2, 3 и 4 м/с, а дискретность времени соответствует 1 с, то переходы между состояниями 1    , и       соответствуют ускорению по модулю 1 м/с2. Переходы между состояниями         и 2 <^> 4 соответствуют ускорению по модулю 2 м/с", а переход между состояниями 1 ^ 4 соответствует ускорению по модулю 3 м/с2.

Цепь Маркова высшего порядка позволяет устанавливать соответствие между рядом последовательных состояний системы в прошлом и вероятностями перехода в определённые состояния в будущем. Длина цепи соответственно определяет количество учитываемых шагов в прошлом.

Применительно к ветроэнергетике это означает определённую вероятность при заранее известной последовательности изменений скорости ветра в прошлом. Так, известно, что если в ветреный день ветер стихает (то есть его скорость становится равной 0), то чем дольше длится период затишья, тем больше вероятность того, что в следующую секунду ветер появится снова.

Аналогично, если ветер усиливается некоторое количество шагов подряд, цепь Маркова позволяет спрогнозировать вероятность его дальнейшего роста или падения. Именно в этом и состоит способность цепей Маркова к прогнозированию вероятности тех или иных событий на основе данных о предыдущих состояниях системы. Таким образом, можно утверждать, что цепь Маркова обладает «памятью».

Преимущества цепи Маркова перед вероятностью распределения скоростей ветра состоят в том, что цепь Маркова позволяет исследовать режимы работы ветро- установок при изменении скоростей ветра. Часто подобные исследования проводятся при условии заранее заданной предельной скорости изменения ветрового потока.

Кроме этого, цепи Маркова хорошо поддаются автоматизации и позволяют в автоматическом режиме рассчитать не только вероятность той или иной динамики скорости ветра, но и вероятность появления тех или иных переходных режимов ветроустановки.

В настоящее время применяется метод расчёта, основанный на измерении скорости ветра на протяжении достаточно длинного периода времени (обычно используется один год), с последующим введением в математическую модель этих скоростей ветра в качестве входных данных с целью определения выработки ветроустановки. Такой подход позволяет рассчитывать переходные режимы работы установки и с высокой точностью определять конечный результат, но он обладает недостатком, который заключается в количестве экспериментальных данных, необходимых для такого определения. Так, если измерять скорость ветра каждые 10 секунд в диапазоне 0-24 м/с с шагом 0,75 м/с (что обеспечит 5 двоичных разрядов или 32 бита информации), то измерения на протяжении года потребуют почти 2 Мб сжатых необработанных данных. Увеличение частоты опроса до 1 секунды потребует уже 20 Мб.

Но система, основанная на фактических данных, позволяет прогнозировать, как установка работала бы в прошлом, но не в будущем. Несмотря на то, что скорости ветра имеют тенденцию к повторению, и прогнозирование на основе этих данных достаточно точно, применение цепей Маркова позволяет рассмотреть вероятность изменения скорости ветра.

Цепи Маркова позволяют исследовать порывистый характер ветра, что немаловажно не только для исследований и моделирования ветроу станов ок, но и при исследовании характеристик самого ветрового потока.

Таким образом, цепи Маркова представляют собой достаточно мощный ин- струмент для описания изменения скорости ветра с учётом его динамики, то есть описывать не только вероятностное распределение скоростей ветра, но и вероятности её изменения, что позволяет проводить исследования ветроустановок на математических моделях не только в заданных условиях, когда точно определены величины и динамика скорости ветра, но и в «приближённых к реальным» условиях, когда точное изменение скорости ветра не определено, а лишь задано с определённой вероятностью.

В этом случае цепь Маркова высшего порядка позволяет создавать стохастическую модель динамики скорости ветра.

Выводы Совмещение исследований ветроустановки с заранее заданными скоростями ветра и динамикой их изменения для того чтобы определить предельные режимы работы ветроустановки с испытаниями с помощью цепи Маркова, позволяют провести более полное исследование ветроустановки. Цепь Маркова позволяет установить вероятность появления тех или иных ветровых режимов (характеризующихся не только скоростью ветрового потока, но и динамикой его изменения) и установить вероятность появления ветровых режимов, которые могут быть опасны для установки.

Следует отметить преимущество цепей Маркова высших порядков в этом случае, поскольку они позволяют прогнозировать вероятность быстрого и значительного нарастания скорости ветрового потока или его резкий спад.

Для построения цепи Маркова следует воспользоваться достаточным объёмом накопленных экспериментальных данных для определения вероятностей перехода в цепях событий, а с увеличением длины цепи Маркова объём требуемых экспериментальных данных быстро возрастает.

Следует отметить, что хотя математическое моделирование и позволяет проводить достаточно «реалистичные» исследования устройств и процессов на математических моделях, оно не способно и никогда не будет способно заменить экспериментальные исследования. Его важная роль заключается в обеспечении возможности «предвидеть» результаты экспериментальных исследований без проведения натурных экспериментов.