Применение динамического частотно-импульсного модулятора для управления процессом производства и качества молочной продукции
Автор: Алдибекова А.Н.
Журнал: Вестник Алматинского технологического университета @vestnik-atu
Рубрика: Техника и технологии
Статья в выпуске: 1 (102), 2014 года.
Бесплатный доступ
Статья посвящена моделированию автоматизированной системы управления процессом производства и качества молочной продукции с динамической частотно-импульсной моду-ляцией, фильтр которой реализован в виде апериодического звена 2-порядка (ДЧИМ с ФАЗ). Получены уравнения ДЧИМ с ФАЗ 2-порядка для управления режимными параметрами производства молока. Построена структурная модель ДЧИМ с ФАЗ 2-порядка, процессы которой тождественны процессам в реальном модуляторе. Полученная в данной работе структурная модель модулятора служит основой для построения математических моделей динамической частотно-импульсной системы управления производства и качества молочной продукции, которые позволяют в дальнейшем разработать различные по точности и трудоемкости вычислительных процедур методы анализа и синтеза рассматриваемого в статье класса систем производства молока частотно-импульсных систем управления.
Автоматизированная система управления, динамический частотно-импульсный модулятор, вольтеровская модель, фильтр в виде апериодического звена 2-порядка
Короткий адрес: https://sciup.org/140204709
IDR: 140204709 | УДК: 681.501
Текст научной статьи Применение динамического частотно-импульсного модулятора для управления процессом производства и качества молочной продукции
При использовании в АСУ первичных преобразователей, основанных на различных физических явлениях, позволяющих повысить точность и качество регистрируемых входных и выходных параметров, необходимо разрабатывать более совершенные регулирующие элементы.
Объекты и методы исследования
Применяется метод для преобразования эквивалентной ДЧИМ с ФАЗ 2-порядка нелинейной системы, названной в даль-
Результаты и их обсуждение
Динамические частотно-импульсные системы автоматического управления (ДЧИСАУ) производства молочной продукции представляют собой замкнутую систему, состоящую из динамического частотноимпульсного модулятора с фильтром в виде апериодического звена 2 порядка (ДЧИМ с ФАЗ) и приведенной непрерывной части (ПНЧ), структурная схема которой представлена на рис.1 [1].
нейшем структурной моделью.
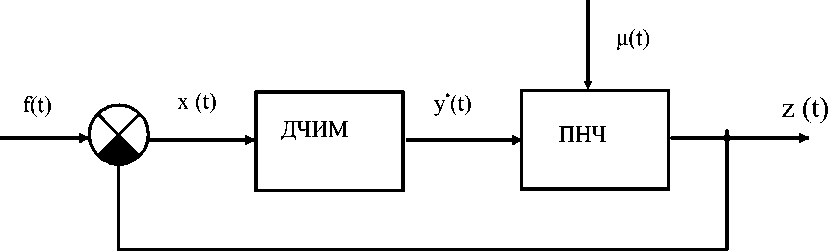
Рисунок 1 - Структурная схема ДЧИСАУ производства молочной продукции.
На входе системы управления производством молочной продукции действует стационарный случайный процесс f ( t ). Прямая цепь состоит из импульсной и приведенной непрерывной частей. Импульсной частью служит ДЧИМ, преобразующий x(t)
процесс ошибки в частотно-модулиро-ванную последовательность δ -импульсов Дирака y (t) .
Приведенная непрерывная часть ПНЧ состоит из последовательного соединения управляемого объекта с запаздыванием, исполнительного механизма (ИМ) и формирующего элемента (ФЭ), задающего требуемую форму управляющим импульсам.
Объект с запаздыванием подвержен воздействию внешнего белого шума
µ (t) . В
общем случае ПНЧ характеризуется как нелинейная динамическая система со случайными параметрами и представима некоторым функциональным уравнением следующего вида [2]:
z(t) =H[λ, τ0, z(τ), g(τ) /t0 ≤τ≤t]
где H
-
непрерывный нелинейный
функционал; параметр λ характеризует слу- g(t)
чайность параметров функционала H; -последовательность управляющих случайных
в сигнал
y(t) , а импульсное устройство ИУ
генерирует единичный δ -импульс в тот
момент времени, когда
y(t)
достигает
τ импульсов заданной формы; 0
-
время
запаздывания управляемого объекта управления.
ДЧИМ с ФАЗ 2- порядка представляет собой последовательное соединение фильтра Ф и импульсного устройства ИУ. В фильтре Ф осуществляется некоторое динамическое x(t) преобразование непрерывного сигнала
порогового значения ± Δ и осуществляет обнуление всех накопителей энергии, которые входят в состав Ф [3].
Допустим, что в некоторый момент t n на выходе ИУ появился n-й импульс. Тогда
момент появления tn + 1 (n+1)-го импульса с
учетом свойств объекта с запаздыванием будет определяться таким образом:
t n + 1 - 0
y(tn+1 -0)= ∫w(tn+1 -τ)x(τ)dτ=λn+1Δ tn+τ0
где
λ n + 1 = y(tn + 1 - 0)
,
w(t) = L {W(p)}– весовая функция этого преобразования; W(p)– передаточная
τ
функция фильтра Ф, m– параметр динамического частотно-импульсного модуля- тора, учитывающий эффект запаздывания управляемого объекта ( τ m ≥ τ 0 ) [1].
Cтруктурную модель ДЧИМ с ФАЗ 2-порядка можно формировать в виде замкнутой нелинейной системы, структурная схема которой изображена на рис. 2 [2].
x(t) u(t) v(t) y ∗ (t)

Рисунок 2 - Нелинейная эквивалентная система.
φ(u)
-5 -4 -3 -2 -1
-2
-3
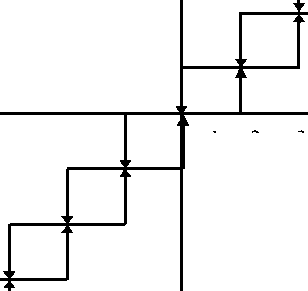
Рисунок 3 - Характеристика релейно-гистерезисного элемента.
1 2 3 4 5
-1
u
Она содержит нелинейный фильтр, который характеризуется некоторым опера- тором
А[ т m ,x( T ), y ( T )/t 0 T' t]
, релейно-гистерезисный нелинейный элемент
ф (и)
1 7 (рис.3) с порогом A и дифференцирующий элемент с передаточной функцией Wg ( p ) = p [1].
Задача заключается в определении вида нелинейного оператора А, при котором замкнутая система, показанная на рис. 2, генерирует такую же последовательность импульсов, что и ДЧИМ при управлении объектами с запаздыванием и описываемый уравнениями (2) и (3).
Построение такого нелинейного оператора А рассмотрим для ДЧИМ с ФАЗ 2-порядка, используемых для управления объектами производства молока.
ДЧИМ, фильтр которого реализован в виде апериодическое звена 2-порядка, характеризуется передаточной функцией:
W ( P ) = -„ (4)
p + ap + в
Если в фильтре модулятора корни характеристического полинома вещественные и отрицательные, то указанную функцию можно разложить в виде:
к 1 1
W ( p ) =------- () (5)
a2 — « 1 p + a2 p + « 1
В дальнейшем для простоты системы k обозначим =k μ.
a2 — a
В соответствии с уравнением (2) и (3) для модифицированного ДЧИМ с фильтром апериодического звена 2-порядка моменты появления t n + 1 импульса определяются из уравнения:
t n + 1 -0
y v ( t n + 1 - 0) = к ц J exP( — « 2 ( t n + 1
t n + 1 —0
— т )) x ( t ) dT — к ц J exp( — a 1 ( tn + 1 — т )) x ( t ) dT = Xn + 1 A
t +T t n + T m
t +T tn + Tm
где tn+1-0 tn+1-0
k n + 1
= к ц J exP( — a 2 ( t n + 1 — T )) x ( T ) dT — k ^ J exP( — a 1 ( t n + 1 — T )) x(T ) dT = xn + 1 A
/ +T t +T tn + Tm
tn + Tm kμ - коэффициент усиления а периодического звена 2-порядка.
Рассмотрим произвольный момент времени tn . Пусть выходной сигнал в этот момент времени равен y v ( t n + 0) .
Тогда для моментов времени t > t n
t
y, (t) = ea2( - -tn’ y, (tn + 0) + k, J e tn
—I
t
a2(t—T)x(t)dT - e-ai(t—tn)y, (tn + 0) + k, J e tn
—г
a i( t — T ) x ( t ) dT (7)
где y ν ( t ) - выход фильтра при ном условии y v ( t n + 0) .
началь-
Уравнение (7) перепишем в следующем виде:
yv (t) = e
—(
t n + T m
°■(t"tn)y, (tn + 0) + k,[ Je tn +0
—t
t n + i — 0
"a 2( tT) x (t ) dT + J e tn +Tm
—t
■a2( t—T) x (T ) dT] —
—(
-e
t +T t n + T m
a,(t—tn*y,(tn + 0) + k,[ Je tn +0
—
t n + i — 0
" “i( tT) x (t ) dT + J e t +T nm
—
" “ i( t — T ) x ( t ) dT ]
Из сопоставления (6) и (8) следует, что y , ( t ) = y , ( t ) , если
y,(t) = e
—t
t n + T m
■a 2( t — t n ) y , ( t n + 0) + k , J e t n + 0
—(
t n + i — 0
a2(t—T)[x(t) — ,(t)]dT + k, Je tn +Tm
—t
"a2(t T)x(t)dT —
—k, J e—
■а2(t тП(т)dT - e
—(
t n + T m
■a i( t — t n ) y , ( t n + 0) + k , J e t n + 0
—t
ai(t T)[x(t) — ,(t)]dT +
t n + i — 0
+ k , J e t n + T m
—
"ai(t T)x(t)dT - k, j e
—
"а1( t—T )п(т) dT
где П(t) = s(t)yV(-) kµ
импульсная переходная функция форми-
А для формирования сигнала µ ( t ) представим в виде произведения двух сигналов
рующего звена второго порядка;
s(t) связан с выходным модулятора y* (t) [2]:
сигналом
,(t) = x(t) x(t),
s (t) = 5( t — tn + 0)
Тогда структурную модель
фильтра
где
t
x(t) = J^T„(t — T)dT , tn
К (t)=L—
1 — exP(—Tm • P)
р
–
ДЧИМ а, периодического звена 2-порядка будет формировать в виде замкнутой не линейной системы (рис.2).
Далее рассмотрим преобразование сигнала u ( t ) , осуществление в релейногистерезисном элементе (РГЭ) v = ф( u ) . (рис.3).
Если в некоторый момент времени tn — 0 сигнал u (t) имеет значение u (tn — 0), то следующий момент переключения tn+1 — 0 определяется уравнением u (tn+1 — 0)- u (tn — 0) = Хп+1^, (14) где хп+1= siqn[u(tn+1— 0)-u(tn- 0)]. (15)
При выполнении условий (14) и (15) происходит переход сигнала v(t) с одного уровня на другой и производная сигнала v(t) определяется выражением dv(t)
- Х п + 1 5 ( t — t n + 1 + 0). dt
Из сравнения (8) и (13) можно заключить, что выходной сигнал импульсного устройства ИУ
У ■ (t) - dF - Х+1»( t — tn .1 + 0).(17)
dt
С учетом (17) и (13) сигнал s ( t ) можно формировать следующим образом:
s(t) - y' (t) y^ - y• (t) y^—0) .(18)
AA
Из сопоставления (6), и (14), (15) следует, что
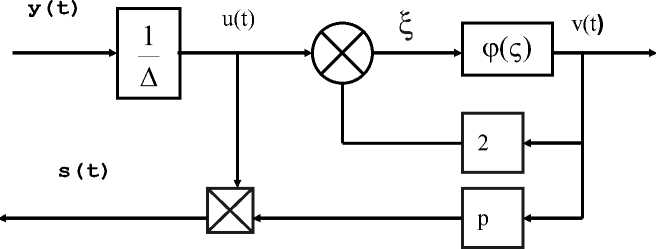
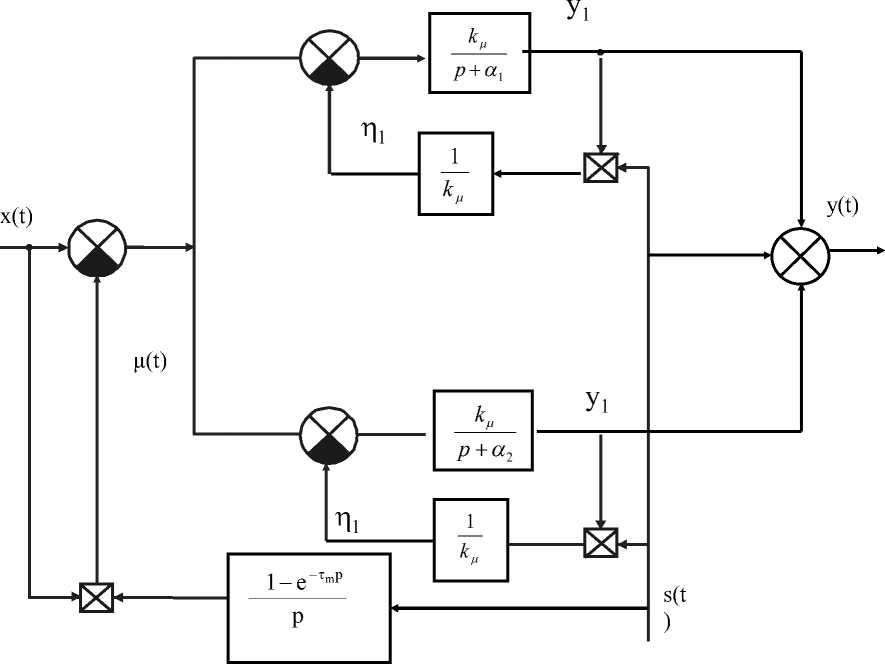
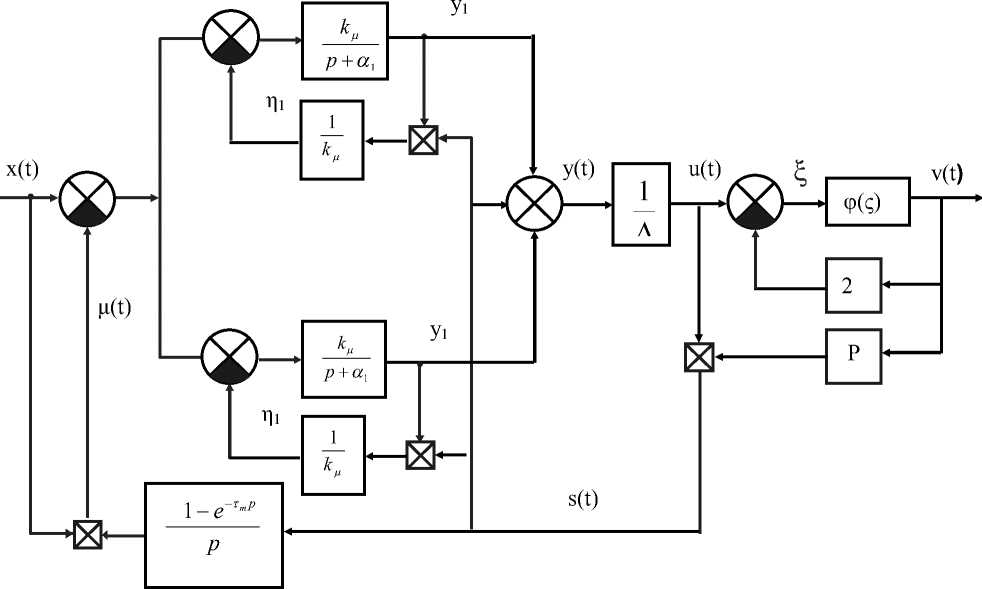
У(t)-u(t) — u(tn — 0), tn + 0 Отсюда, для сигнала u(tn+1) получим: u (tn+1) - У(tn+1 — 0) — u (tn — 0).(20) Блок, содержащий релейно-гистерезисный элемент v - ф(u) и описываемый уравнениями (17)–(20), назовем блоком формирования импульсов (БФИ). Структурная схема БФИ изображена на рис. 4 а. Путем несложных преобразований в [4] получена эквивалентная схема блока формирования импульсов БФИ (рис.4 б). б) Рисунок 4 - Блок формирования импульсов модели ДЧИМ с ФАЗ 2-порядка. Оставшаяся часть оператора А, поведение которого описывается уравнениями (8)-(13), назовем блоком сброса (БС). Из выражений (8)-(13) следует, что задача определения структуры блока сброса БС сводится к формированию сигналов η(t) и μ(t) [1]. Уравнения (8), (9), (10), (11), (12) описывают поведение блока сброса БС [2]. Структурная схема модифицированного БС изображена на рис. 5. Рисунок 5 - Блок сброса ДЧИМ с ФАЗ 2-порядка. Выходной сигнал y(t) модифицированного блока сброса преобразуется блоком формирования импульсов в мгновенные δ -импульсы. Одни импульсы y • (t) знак и , период повторения которых определяются знаком и интервалом непрерывности сигнала y(t) , являются выходными импульсами модулятора, а другие s(t) всегда в эти моменты поступают обратно в БС. Блок формирования импульсов БФИ структурной модели ДЧИМ с ФАЗ 2-порядка совпадает с соответствующим блоком структурной модели ДЧИМ [2], т.е. он является универсальным для всех видов ДЧИМ. Рассмотрим блок сброса (рис. 5). Как видно из рис. 5, в структуре модифицированного блока сброса присутствует дополнительный блок формирования сигнала µ(t) , описываемого соотношениями (11)(12). Назначение этого дополнительного блока заключается в формировании сигнала, принудительно удерживающего выход интегратора y(t) в нулевом положении после выдачи импульса управления в течение времени запаздывания объекта. Вышеуказанные особенности блока сброса БС приводят к изменениям свойств системы. В структурной модели ДЧИМ с ФАЗ 2-порядка только блок сброса БС [1] зависит от свойств фильтра в модуляторе. В связи с этим процедура построения структурной модели других типов ДЧИМ будет отличаться от приведенной процедуры только процедурой построения структуры блока сброса. Рисунок 6 - Полная структурная схема модели ДЧИМ с ФАЗ 2-порядка. Объединяя структурные схемы блока сброса (рис. 5) и блока формирования импульсов (рис. 4), получим структурную схему системы (рис. 6), эквивалентной ДЧИМ с ФАЗ 2-порядка, но не содержащий параметрических обратных связей. Выводы и заключение На основе структурной модели модулятора разработаны математические модели динамической частотно-импульсной системы. Процессом управления производства и качества молочной продукции в классе функциональных рядов Вольтерра, которые позволяют в дальнейшем разработать различные по точности и трудоемкости вычислительных процедур методы анализа и синтеза рассматриваемого в статье класса систем производства молока частотноимпульсных систем управления.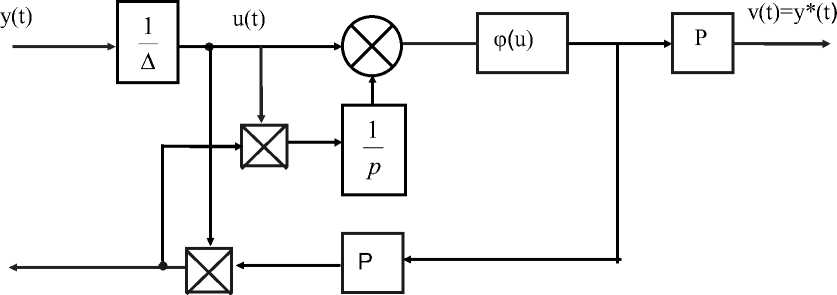
Список литературы Применение динамического частотно-импульсного модулятора для управления процессом производства и качества молочной продукции
- Айтчанов Б.Х. Методы математического описания частотно-импульсных систем управления объектами с запаздыванием.//Вестник КазНТУ. -Алматы: КазНТУ. -2002. -№2. (30). -С.72-82.
- Айтчанов Б.Х. Модели динамических частотно-импульсных систем автоматического управления объектами с запаздыванием//Модели и методы автоматизации управления производственными системами. -Алматы: КазНТУ. -1996. Вып. 2. -С. 65-73.
- Айтчанов Б.Х. К построению математических моделей одного класса стохастических систем управления объектами с запаздыванием//Энергетика, телекоммуникация и высшее образование в современных условиях. Алматы; АИЭС. -1998. -С.108-110.
- B. Kh. Aitchanov, B. K. Kurmanov, and T. F. Umarov//Dynamic pulse-frequency modulation in objects control with delay. Asian Journal of Control, Vol. 14, No. 5, PP. 1-7, September 2012.-Published online in Wiley Online Library (wileyonlinelibrary.com) DOI: DOI: 10.1002/asjc.471


