Применение фильтра Калмана в задаче технической диагностики двигателей внутреннего сгорания

Одним из эффективных методов фильтрации в условиях нестационарности сигналов является использование фильтра Калмана [1].

При применении этого подхода к задаче диагностики состояния ДВС следует учесть, что в рассматриваемом случае при работе ее виброакустический сигнал, воспроизводимый каждым из узлов этого объекта, имеет взаимокорреляцию друг с другом. Поэтому, исходя из идеологии теории клеточных автоматов [2–4], при решении задачи фильтрации сигналов необходимо производить параллельные измерения и совместную обработку виброакустических сигналов для смежных узлов ДВС. Например, если производятся измерения сигнала на первом блоке цилиндров ДВС, следует регистрировать вибросигнал и на втором блоке цилиндров.

Поэтому с учетом этого, рассматривая ДВС как динамическую систему, с которой снимаются случайные одномерные виброакустические сигналы, можно записать для первого и второго канала измерений следующую систему стохастических дифференциальных уравнений для фильтра Калмана:

dx^ = f (t) x (t) + r (t), f (0) = f,;(1)

dt z (t) = c (t) x (t) + d (t) n (t);(2)

drt) = q(t) r(t)+ a(t) m(t);

Ц( t) = g(t )* r(t)+ b(t) v(t).(4)

Автокорреляционную функцию случайных процессов r(t), n(t), m(t), v(t) можно представить в следующих видах:

R rr ( t , t ) = Q ( t )* 5 ( t — t ); ' R m ( t , t ) = N ( t )* 5 ( t -t );

R_mm ( t , t ) = M ( t )* 5 ( t -t );

Rvv (t, t) = V (t, t) * 5( t -t), где Q(t), N(t), M(t), V(t) - известные детерминированные функции, а 8(t -t) - функция Дирака.

В уравнениях(1) и (4) f ( t ) и q ( t ) считаются известными и детерминированными функциями.

В данной задаче приняты следующие условия:

процедура оценки линейная;

оценка несмещенная MX = Mx = x ;

оценка x - эффективная Dx = min.

Здесь вектор состояния x динамической системы, который является случайным гауссовским процессом, в данном случае вектор состояния x , шум измерения являются гауссовскими случайными процессами с нулевым математическим ожиданием. Поэтому примем модель белого шума в системе и в измерениях.

Рассматривая регистрируемый виброакустический сигнал как одномерный дискретный процесс и исходя из выше принятых условий, запишем рекуррентные уравнения для фильтров Кальмана. Для первого блока цилиндров ДВС:

x (k +1) = F (k) x (k) + r (k);(6)

z (k) = Cx (k) + n (k)(7)

и для второго блока цилиндров ДВС:

d (k +1) = D (k) d (k) + m (k);(8)

ц( k) = G (k) d (k) + v (k),(9)

где r ( k ), n ( k ), m ( k ), v ( k ) - белые шумы M [ ( r ( k ) ) ] = 0, M [ ( n ( k ) ) ] = 0, M [ ( m ( k ) ) ] = 0, ^M [ ( ^{v ( k} ) ) ] = ⁰ и с ковариационными матрицами:

cov[r(k),n(k)] = 0, cov[m(k),v(k)] = 0, cov[r(k),r(k)] = R(k)*8(t-t), cov[n(k),n(k)] = N(k)* 8(t -t), cov[x(k)x(k +1)] = Px(k).

В данной задаче приняты следующие условия:

процедура оценки линейная;

оценка несмещенная Mx = Mx = x ;

оценка x - эффективная Dx = min. Так как оба фильтра являются идентичными, поэтому рассмотрим синтез первого фильтра Калмана.

Исходя из этих условий, выбираем структуру первого фильтра в виде

x(k) = H^(k) + Kz(k), где H и K необходимо определить из условия несмещенности оценки xˆ.

x ( k + 1) = Hx ( k ) + K [ Cx ( k ) + n ( k ) ] ^ Hx ( k ) + KCx ( k ) + Kn ( k ) ^ F ( k ) x ( k ) + r ( k ).

Откуда

Hx(k) = [ F ( k ) - KC ] x ( k ) + Kn ( k ) + rk\

Учитывая, что среднее значение входного белого шума n ( k ), r ( k ) равны нулю, имеем H = F ( k ) - KC .

Матрицу H определим из условия эффективности оценки x ˆ( k ), то есть

Dx = min D (x (k) - x ) ^ min (trPe), где tr() - след ковариационной матрицы; Pe - ковариационная матрица ошибки e(k). Для определения минимума trPe запишем e (k) = (x - x) = [ F (k) x (k) + r (k)] - [ H^k) + KZ(k) ] = [ F (k) x (k) + r (k)] - [ F (k) - KC ] X(k) +

+ KCx ( k ) + Kn ( k ) = F ( k ) [ x ( k ) - x ( k ) ] - KC [ x ( k ) - x ( k ) ] + r ( k ) + Kn ( k ) = F ( k ) * e ( k ) -

• - KC * e (k) + r (k) + Kn (k).(11)

В результате имеем уравнение Риккати и ковариационную функцию следующего вида e (k) = (x - x) = [ F (k) - KC ] * e (k).

Следовательно, ковариационная матрица ошибки будет определяться

Pe =[ F(k) - KC] Pe + Pe [F(k) - KCf + KT + KRKT.(12)

При ^P = 0 имеем - CTP - CTP + 2KR = 0, dK тогда коэффициент усиления фильтра рассчитывается следующим образом:

K = CTPe * R-1.(13)

Алгоритм рекурсивного обновления оценки x ˆ( k ) соответствует следующей системе уравнений:

Z(k ) = C ( k ) F ( k ) x( k - 1) - прогнозируемое значение наблюдаемого сигнала;

s ( k ) = z ( k ) - z(k ) - невязка между прогнозируемым и реальным наблюдаемыми сигналами.

Поэтому для дискретного случая измерения наблюдаемого сигнала имеем:

K ( k ) = P ₆ ( k - 1) C T ( k )* |^ C ( k )* P _s ( k - 1) C T ( k ) + Q ( k ) ] - коэффициент усиления стационарного фильтра Калмана;

Jc( k ) = F ( k )J x ( k - 1) + K ( k ) s ( k ) - обновление оценки процесса x ( k );

P e ( k ) = F ( k ) [ P _£ ( k - 1) - K ( k ) C ( k ) P _E ( k - 1) ] F T ( k ) + Q ( k ) - обновление ковариационной функции ошибки.

Вектор коэффициентов - w фильтра Калмана при адаптивной фильтрации наблюдаемого сигнала не является детерминированным, поэтому матрица перехода F ( k ) = I , а в качестве наблюдаемого сигнала используются сигналы, получаемые с линий задержек фильтра. Выходной сигнал фильтра при этом представляет собой прогнозируемое значение наблюдаемого сигнала, а в качестве образцового сигнала ц ( k ) вступает сигнал, поступающий от смежного блока цилиндров ДВС. В этом случае шумом наблюдаемого сигнала является невязка между воспроизводимым сигналом фильтра и образцовым сигналом ц ( k ), а матрица шума системы

E <®ktoT ^А(k - i)Qk , где Qk превращается в скалярный параметр.

Величина этого параметра слабо влияет на результат фильтрации, и она, может быть, принята в пределах - [ 0,001 ^ 0,01 ] ст 2 [5].

Следовательно, вышеуказанные формулы принимают следующий вид:

y ( k ) = u^T ( k ) iw( k - 1) - выходное прогнозируемое значение образцового сигнала;

K ( k ) = ( P ₆ ( k )( k - 1) u ( k ) ) / ( u ^л T ( k ) P ₆ ( k - 1) + Q_k ) - коэффициент усиления фильтра;

w ( k ) = w ( k - 1) + K ( k ) s ( k ) - обновление оценки коэффициентов адаптивного фильтра Калмана;

P ( k ) = р ( k - 1) - K ( k ) u^Tp ( k - 1) + Q_k - корректировка оценки ковариационной матрицы ошибки.

Классический вариант фильтра Калмана был смоделирован в среде программного продукта MATLAB/Simulink [6] (рис. 1, 2).

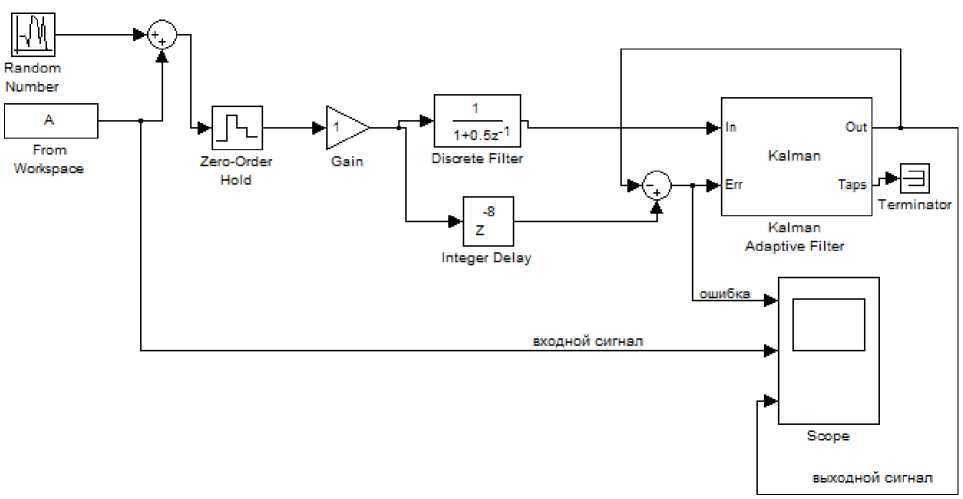
Рис. 1. Структурная схема моделирования фильтра Калмана

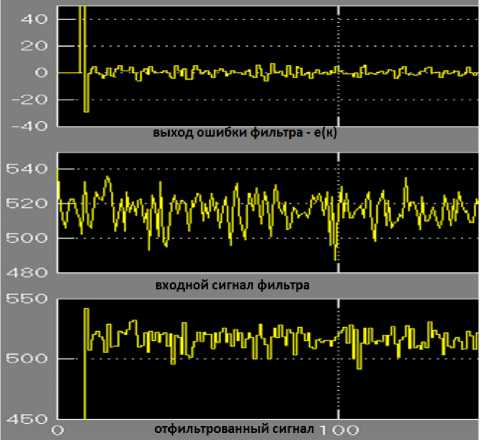
Рис. 2. Результаты моделирования фильтра Калмана

В данной работе также сконструирован прибор на базе микроконтроллера Ardiuno Mega, включающий в себя виброакустическое измерительное устройство и фильтр Калмана. Так как классическая форма реализации данного фильтра на этом микроконтроллере не представляется возможным, поэтому были использованы следующие алгоритмы:

xk = Fxk -1 + rk -1, где Xk - предсказание состояния системы в текущий момент времени;

X k - 1 - предсказание состояния в предыдущий момент времени.

Прогнозируемое значение ошибки ковариации:

P = FP k - 1 F T + Q r .

Здесь P k - предсказание ковариации ошибки; P - - ковариации ошибки в k - 1-м шаге; Q r - ковариации шума процесса.

Определение коэффициента усиления фильтра:

P * H T k , H * Pk * HT + R где Kk - коэффициент усиления фильтра; H - матрица, отображающая отношения измерений и состояний; R - ковариация шума измерения.

Обновление с учётом измерения текущего значения z_k :

x k = x k ^K k *⁽ z k ^-

H * x _k ).

Обновление ошибки ковариации:

Pk = (I - Kk * H )* Pk, где I - единичная матрица связи.

Чтобы наглядно продемонстрировать эффективность фильтра Калмана, для задачи диагностики ДВС была произведена фильтрация виброакустического сигнала, которая от микроконтроллера Arduino Mega передается через порт UART компьютера (рис. 3) и записывается в программе Excel 2016.

Для чёткого приема сигнала от ДВС виброакустический датчик закреплен к корпусу двигателя автомобиля марки Opel Vectra выпуска 1997 г.

Рис. 3. Экспериментальная система измерения и фильтрации виброакустических сигналов ДВС автомобиля марки Opel Vectra

Было рассчитано среднеквадратическое отклонение для массива значений, измеренных с помощью виброакустического датчика, и оно составило R = 0,48 . А значение Q в соответствии с рекомендацией [5] равно 0,002.

Из приведённого графика (рис. 4) видно, как среднеквадратическая ошибка фильтра Калмана в процессе адаптации стремится к нулю, это указывает на то, что отфильтрованный сигнал приближается к своему истинному значению.

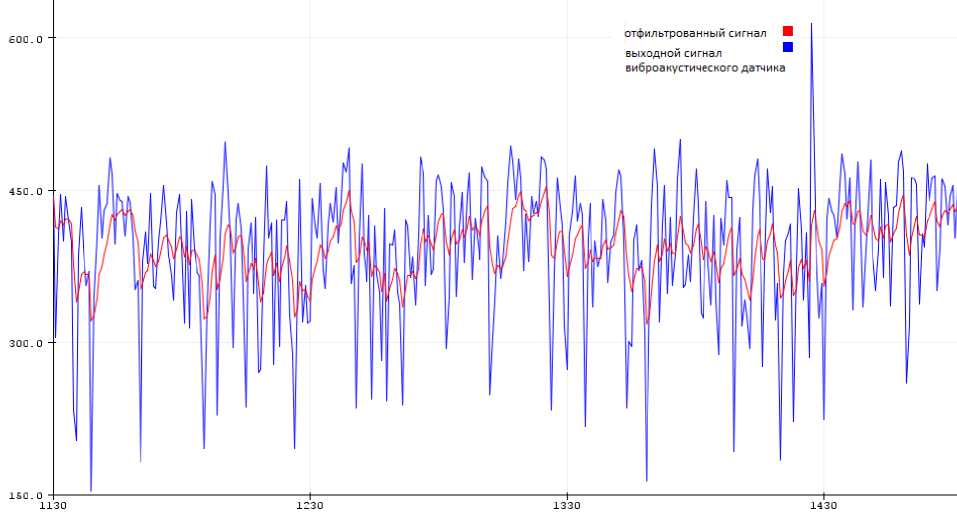
Рис. 4. Графики зашумленных и отфильтрованных виброакустических сигналов ДВС автомобиля марки Opel Vectra