Применение комплексных чисел в финансовых операциях

В данной работе предлагается новый подход при моделировании периодических процессов в экономике с использованием комплексных чисел в качестве процентных ставок. Это приводит к введению комплексных денег, дополняющих реальные деньги неким внутренним качеством.

APPLICATION OF COMPLEX NUMBERS IN FINANCIAL TRANSACTIONS

S.P. Trofimov

In this paper we propose a new approach for modeling of batch processes in the economy using complex numbers as interest rates. This leads to the introduction of integrated money, real money supplementing some inner quality.

Комплексные числа появляются в науке иногда в достаточно экзотической форме. Например, гипотетические тахионы – частицы, которые могут перемещаться со скоростью, большей скорости света. Если предположить, что масса покоя этих частиц – комплексная, то их масса в движении будет вещественным числом. В этом случае противоречия с теорией относительности Эйнштейна не возникает.

Количество применений комплексных чисел в экономике невелико. В результате изложение комплексного анализа при изучении экономических дисциплин в вузе кажется изолированным.

Как известно, наращение капитала может проходить несколькими способами. На практике, как правило, используется наращение по [сложной] [годовой] [процентной] ставке. Каждое из выделенных слов можно заменить рядом других понятий с существенным изменением формулы расчета наращенной суммы. Например, можно использовать простую учетную ставку.

Важной иллюстрацией финансовой операции является график наращения. Так, при наращении по сложной годовой процентной ставке графиком является экспонента. Другие способы наращения графически представляются прямыми, гиперболами. При переменной процентной ставке графики могут быть достаточно сложными. В любом случае мы имеем дело с обычными графиками функции одной вещественной переменной (рисунок 1).

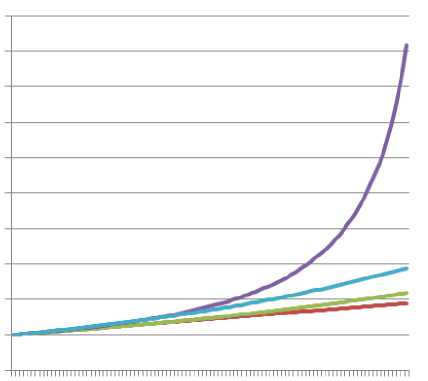
Рис. 1. Традиционные способы наращения

Трофимов С. П.

Основным недостатком стандартных способов наращения капитала является ложное и вредное для банковской системы ощущение, что операцию можно прекратить в любой момент.

Комплексные числа _z = a + b . i расширяют понятие вещественного числа. Они подчиняются тем же операциям, что и обычные числа: сложение, умножение, возведение в степень, извлечение корней. Другими словами, комплексные числа образуют такое же алгебраическое поле, каким является множество вещественных чисел. Единственное отличие заключается в отсутствии важного для экономики свойства полной упорядоченности комплексных чисел.

Комплексные числа имеют три способа представления. Классический способ _z = re + im . i позволяет представить число на комплексной декартовой плоскости. Тригонометрический способ представляет число z = mod - ( cos a + i • sin a ) в полярной системе координат. Здесь od = ( re ² + im ² ) 1^/2 -модуль числа _z , a = arctg ( b / a ) - аргумент числа z . Экспоненциальный способ изображает число в виде _z = mod . e^{i a} .

Рассмотрим наращение по сложной процентной ставке:

FV = PV . ( 1 + r ) t , (1) где начальная сумма PV наращивается в течение срока t по ставке r . Всегда предполагалось, что ставка r – вещественное число. Предположим, что ставка r является комплексным числом _r = a + b • i . Тогда при анализе свойств финансовой операции наращения мы можем изменять два параметра: вещественную и мнимую часть ставки r ^. Рассмотрим тригонометрическую фор-

Тогда по формуле Муавра наращение (1) получает вид

FV = PV . ( 1 + r ) t = PV • ( mod . ( cos a + i • sin a ) ) t = = PV . mod t . ( cos ta + i . sin ta ) (3)

После наращения по формуле (3) комплексную составляющую числа FV можно отбросить и рассматривать в качестве реальной денежной суммы только вещественную часть pv . mod t . _cos t _a . Мы наблюдаем синусоидальные колебательные явления при наращении капитала. В экономике это встречается очень часто. Например, сезонные колебания.

Отметим, что график наращения комплексной суммы FV по формуле (3) в комплексной плоскости представляет собой спираль, которая пересекается с вещественной осью в ее положительной и отрицательной части. Например, при ставке комплексной ставке r = a + 1,09 . i по формулам (2) получим график наращения на рисунке 2. Период наращения капитала составляет 5 лет, коэффициент роста капитала за этот период равен 2.

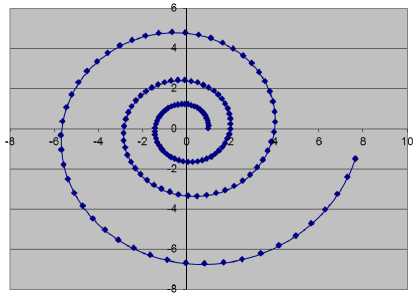
Рис. 2. Комплексная наращенная сумма му представления комплексного числа z , участвующего в формуле наращения (1):

z = 1 + r = ( 1 + a ) + b . i = mod . ( cos a + i . sin a )

2         1/2

mod = ( ( 1 + a ) + b ² ) ,                (2)

При переходе к вещественным деньгам можно отбросить мнимую составляющую наращенной комплексной суммы. Тогда мы получим график на рисунке 3.

где a = arctg ( b / ( 1 + a ) ) .

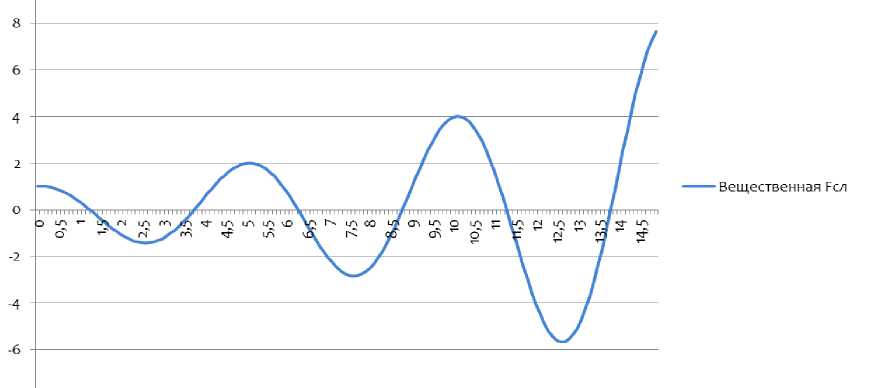
Рис. 3. Вещественная часть наращенной комплексной денежной суммы

Это можно интерпретировать следующим образом. После начала финансовой операции в определенные моменты времени наращенная сумма FV остается положительной, то есть можно прекратить операцию с прибылью. Спустя некоторое время выход из операции приведет лишь к значительным убыткам, но спустя еще определенное время мы снова получаем еще большую прибыль и т. д.

Из депозитов с различными комплексными ставками можно составлять портфели ценных бумаг. На рисунке 4 представлена сумма двух комплексных вкладов. Меняя весовые коэффициенты вкладов в этой сумме, можно добиться желаемых свойств итогового портфеля.

Модуль комплексного числа z = 1 + r определяет скорость роста капитала, а его аргумент задает временной период, через который можно прекращать операцию с наибольшим положительным доходом. Вещественная и мнимая части комплексной процентной ставки r одновременно влияют на важные и вполне конкретные характеристики финансовой операции.

Таким образом, комплексная ставка наращения является гибким регулятором важных параметров финансовых операций и может использоваться в юридических документах.

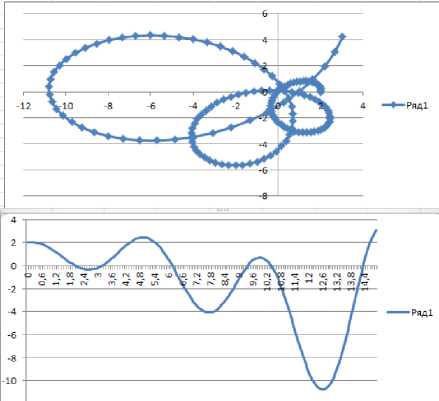
Рис. 4. Сумма двух вкладов с различными комплексными ставками