Применение математической модели нестационарного испарения жидких растворов для описания кинетики сушки фильтрата пивной дробины

Татьяна Германовна Короткова; Александра Сергеевна Данильченко; Tatiana G. Korotkova; Aleksandra S. Danilchenko

doi:10.36718/1819-4036-2021-7-204-210

Применение математической модели нестационарного испарения жидких растворов для описания кинетики сушки фильтрата пивной дробины

Автор: Татьяна Германовна Короткова, Александра Сергеевна Данильченко

Журнал: Вестник Красноярского государственного аграрного университета @vestnik-kgau

Рубрика: Технология продовольственных продуктов

Статья в выпуске: 7, 2021 года.

Бесплатный доступ

Цель исследования – проверка адекватности математической модели нестационарного испарения жидких растворов при вынужденной конвекции для описания кинетики сушки фильтрата пивной дробины. Задачи исследования: экспериментальное исследование кинетики сушки фильтрата пивной дробины и проверка адекватности математической модели нестационарного испарения жидких растворов с инертной поверхности при вынужденной конвекции для описания кривой сушки и кривой скорости сушки. Приведены экспериментальные данные при температуре сушильного агента 60 °С по кинетике сушки фильтрата пивной дробины, полученного путем отжима на механическом прессе сырой пивной дробины пивзавода ООО «Майкопское пиво». Среднее значение содержания сухого вещества двух образцов фильтрата пивной дробины составило 6,26 %. Определено изменение влажности, влагосодержания фильтрата и скорости сушки. Для описания кинетики сушки фильтрата пивной дробины применена ранее разработанная авторами математическая модель нестационарного испарения жидких растворов с инертной поверхности при вынужденной конвекции, представляющая собой совокупность нелинейных уравнений. Получено хорошее количественное и качественное согласование. Относительное отклонение расчетных данных от экспериментальных не превышает 4 %. Наблюдаемый скачок скорости сушки на стыке между периодом прогрева материала и периодом удаления свободной влаги свидетельствует о погрешности или, возможно, сложности описания точки перехода между периодами. Период удаления свободной влаги описан практически прямой линией, что соответствует известным теоретическим и практическим представлениям. Для описания кинетики сушки при удалении связанной влаги рекомендовано учесть адсорбционный эффект взаимодействия влаги с твердым веществом.

Еще

Отходы пивоваренного производства, фильтрат пивной дробины, кинетика сушки, математическое моделирование.

Короткий адрес: https://sciup.org/140254576

IDR: 140254576 | УДК: 663.48 | DOI: 10.36718/1819-4036-2021-7-204-210

Nonstationary evaporation liquid solutions mathematical model application to describe brewer's grains filtrate drying kinetics

The aim of the study is to test the adequacy of the mathematical model of unsteady evaporation of liquid solutions under forced convection to describe the kinetics of drying the filtrate of brewer's grains. Re-search objectives: experimental study of the kinetics of drying the filtrate of brewer's grains and checking the adequacy of the mathematical model of unsteady evaporation of liquid solutions from an inert surface during forced convection to describe the drying curve and the drying rate curve. Experimental data are given at a drying agent temperature of 60 ° C on the kinetics of drying the brewer's grains filtrate obtained by squeezing raw brewer's grains on a mechanical press from the Maykop beer brewery. The average dry matter content of the two samples of brewer's grains filtrate was 6.26 %. The change in moisture content, moisture content of the filtrate and drying rate was determined. To describe the kinetics of drying the filtrate of brewer's grains, the previously developed by the authors a mathematical model of unsteady evaporation of liquid solutions from an inert surface under forced convection, which is a set of nonlinear equations, is used. Good qualitative and quantitative agreement was obtained. The relative deviation of the calculated data from the experimental data does not exceed 4 %. The observed velocity jump in the drying rate at the junction between the period of heating of the material and the period of removal of free moisture indicates an error or, possibly, the complexity of describing the transition point between periods. The period of removal of free moisture is described by an almost straight line, which corresponds to the known theoretical and practical concepts. To describe the kinetics of drying when removing bound moisture, it is recommended to take into account the adsorption effect of the interaction of moisture with a solid.

Еще

Текст научной статьи Применение математической модели нестационарного испарения жидких растворов для описания кинетики сушки фильтрата пивной дробины

Введение. Отходом пивного производства является пивная дробина влажностью 80–90 %, богатая клетчаткой, белками, жирами и незаменимыми аминокислотами [1]. Наибольшее распространение получил способ переработки сырой пивной дробины в сухую кормовую добавку путем механического обезвоживания и сушки [2].

В процессе обезвоживания путем отжима или центрифугирования образуется фильтрат (фугат), который содержит 4–7 % перешедших в жидкую фазу растворимых веществ, таких как сахара, аминокислоты, белковые вещества, клетчатка, безазотистые вещества.

Такой фильтрат с низким содержанием экстрактивных веществ не пригоден для возврата в сусло, а его утилизация в канализацию приводит к возрастанию нагрузки на локальные очистные сооружения. Использование декан-терной центрифуги для извлечения взвешенных веществ из фильтрата пивной дробины не позволило получить прозрачный фильтрат, а применение органических коагулянтов и флокулянтов приводит к их присутствию в сухом остатке после сушки. Исследования по вопросам безопасности содержания коагулянтов и флокулянтов в кормовых смесях для животных еще недостаточно изучены [3]. Несмотря на небольшое количество и размер тонкодисперсных растворимых веществ, плотность фильтрата пивной дробины зависит от процентного содержания экстрактивных веществ и составляет при 6 % порядка 1 024 кг/м3 [4], в связи с чем фильтрат пивной дробины можно отнести к жидким растворам.

Таким образом, механическое обезвоживание приводит к потере питательных веществ с

фильтратом. Извлечение питательных веществ из фильтрата пивной дробины при удалении влаги позволит, с одной стороны, снизить нагрузку на окружающую среду, а с другой – повысить питательную ценность сухой пивной дробины путем ее смешения с сухим остатком фильтрата.

Продолжительность сушки можно определить методом математического моделирования испарения жидких растворов с последующей оценкой энергетических затрат на сушку.

Цель исследования: проверка адекватности математической модели нестационарного испарения жидких растворов при вынужденной конвекции для описания кинетики сушки фильтрата пивной дробины.

Задачи исследования: экспериментальное исследование кинетики сушки фильтрата пивной дробины и проверка адекватности математической модели нестационарного испарения жидких растворов с инертной поверхности при вынужденной конвекции для описания кривой сушки и кривой скорости сушки.

Объект, предмет и методы исследования. Объектом исследования является фильтрат пивной дробины, полученный путем отжима на ручном механическом прессе ПРОМ-1У сырой пивной дробины пивзавода ООО «Майкопское пиво».

Предмет исследования – математическая модель нестационарного испарения жидких растворов с инертной поверхности при вынужденной конвекции для описания кинетики сушки фильтрата пивной дробины при удалении свободной влаги.

Процесс сушки проводили в сушильном

шкафу Memmert UFE 400, оснащенном вентилятором при скорости сушильного агента 4,5 м/с для температурного режима 60 °С. Убыль массы навески фиксировали на весах Ohaus Discovery через 5 мин в течение всего эксперимента. Процентное содержание сухого вещества определяли по ГОСТ 31640-2012. Для этого два образца фильтрата пивной дробины высушивали в сушильном шкафу в течение часа при температуре 105 °С, затем охлаждали в эксикаторе до комнатной температуры и взвешивали. Среднее значение содержания сухого вещества двух образцов фильтрата пивной дробины составило 6,26 %.

Результаты исследования и их обсуждение. Фильтрат пивной дробины имеет насыщенный коричневый цвет, соответствующий цвету пивной дробины. Для определения возможных путей переработки фильтрата и повышения питательности сухой дробины проведен эксперимент по кинетике сушки фильтрата пивной дробины. С этой целью сырую пивную дробину отжали на механическом прессе. Динамика изменения убыли массы навески фильтрата в процессе сушки приведена в таблице. Расчет-

ным путем определены изменение влажности и влагосодержания фильтрата во времени, а также скорость сушки.

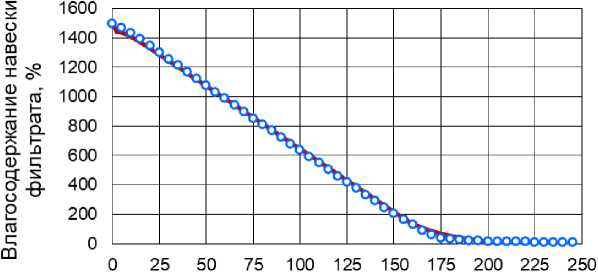
На рисунке 1 приведено изменение окраски фильтрата в процессе сушки в динамике. После высушивания дно бюкса полностью покрыто коричневой пленкой. Полученные экспериментальные данные использованы для построения кривой сушки и кривой скорости сушки (рис. 2, 3). При построении кривой скорость сушки отложена при среднем значении , %, двух рядом стоящих измерений влагосодержания:

Скорость сушки N , мин^-1, определена по выражению

^n+1

N — —

”^n+1

Через 30 мин Через 90 мин Через 150 мин от начала сушки от начала сушки от начала сушки

Рис. 1. Внешний вид фильтрата пивной дробины в процессе сушки

После высушивания

Исследование кинетики сушки фильтрата пивной дробины при температуре сушильного агента 60 °С

Время τ, мин	Масса навески m, г	Влажность w, %	Влагосодержание u, %	Среднее значение двух измерений , %	Скорость сушки N, мин^-1
1	2	3	4	5	6
Экспериментальные данные
0	50,417	93,740	1497,497	1497,497	0
5	49,524	93,627	1469,202	1483,349	5,659
10	48,322	93,469	1431,115	1450,158	7,617
15	47,027	93,289	1390,082	1410,599	8,207
20	45,694	93,093	1347,845	1368,964	8,447

Продолжение табл.

1	2	3	4	5	6
25	44,210	92,861	1300,824	1324,335	9,404
30	42,820	92,630	1256,781	1278,802	8,809
35	41,407	92,378	1212,009	1234,395	8,954
40	39,943	92,099	1165,621	1188,815	9,278
45	38,582	91,820	1122,497	1144,059	8,625
50	37,183	91,512	1078,169	1100,333	8,866
55	35,728	91,167	1032,066	1055,117	9,221
60	34,350	90,812	988,403	1010,234	8,733
65	32,947	90,421	943,948	966,176	8,891
70	31,448	89,964	896,451	920,200	9,499
75	30,048	89,497	852,091	874,271	8,872
80	28,707	89,006	809,601	830,846	8,498
85	27,393	88,479	767,966	788,783	8,327
90	25,994	87,859	723,638	745,802	8,866
95	24,568	87,154	678,454	701,046	9,037
100	23,227	86,412	635,963	657,208	8,498
105	21,873	85,571	593,061	614,512	8,580
110	20,491	84,598	549,271	571,166	8,758
115	19,084	83,463	504,689	526,980	8,916
120	17,655	82,124	459,411	482,050	9,056
125	16,289	80,625	416,128	437,769	8,657
130	15,006	78,968	375,475	395,802	8,131
135	13,639	76,860	332,161	353,818	8,663
140	12,291	74,323	289,449	310,805	8,542
145	10,943	71,160	246,736	268,093	8,542
150	9,646	67,282	205,640	226,188	8,219
155	8,396	62,411	166,033	185,837	7,921
160	7,198	56,154	128,074	147,053	7,592
165	6,009	47,479	90,399	109,236	7,535
170	5,058	37,604	60,266	75,333	6,027
175	4,431	28,775	40,399	50,333	3,973
180	4,089	22,817	29,563	34,981	2,167
185	3,895	18,973	23,416	26,489	1,229
190	3,796	16,860	20,279	21,847	0,627
195	3,716	15,070	17,744	19,011	0,507
200	3,660	13,770	15,970	16,857	0,355
205	3,621	12,842	14,734	15,352	0,247
210	3,590	12,089	13,752	14,243	0,196
215	3,562	11,398	12,864	13,308	0,177
220	3,546	10,998	12,357	12,611	0,101
225	3,528	10,544	11,787	12,072	0,114
230	3,515	10,213	11,375	11,581	0,082
235	3,504	9,932	11,027	11,201	0,070
240	3,490	9,570	10,583	10,805	0,089
245	3,490	9,570	10,583	10,583	0

Окончание табл.

1	2	3	4	5	5
Расчетные данные (период прогрева + первый период сушки)
0	50,417	93,740	1497,497	1497,444	0
5	48,943	93,552	1450,792	1474,144	9,341
10	47,588	93,368	1407,859	1429,326	8,587
15	46,395	93,197	1370,046	1388,953	7,563
20	45,106	93,003	1329,205	1349,625	8,168
25	43,778	92,791	1287,144	1308,175	8,412
30	42,434	92,563	1244,562	1265,853	8,516
35	41,085	92,318	1201,793	1223,178	8,554
40	39,733	92,057	1158,959	1180,376	8,567
45	38,380	91,777	1116,105	1137,532	8,571
50	37,028	91,477	1073,242	1094,673	8,573
55	35,674	91,153	1030,371	1051,806	8,574
60	34,321	90,805	987,491	1008,931	8,576
65	32,968	90,427	944,602	966,046	8,578
70	31,614	90,017	901,704	923,153	8,580
75	30,260	89,570	858,796	880,250	8,582
80	28,905	89,082	815,877	837,336	8,584
85	27,550	88,545	772,949	794,413	8,586
90	26,195	87,952	730,009	751,479	8,588
95	24,840	87,294	687,057	708,533	8,590
100	23,484	86,561	644,093	665,575	8,593
105	22,127	85,737	601,117	622,605	8,595
110	20,770	84,805	558,126	579,621	8,598
115	19,413	83,743	515,121	536,623	8,601
120	18,055	82,521	472,100	493,610	8,604
125	16,697	81,099	429,063	450,581	8,607
130	15,338	79,424	386,007	407,535	8,611
135	13,979	77,423	342,932	364,470	8,615
140	12,619	74,990	299,836	321,384	8,619
145	11,258	71,967	256,716	278,276	8,624
150	9,896	68,109	213,570	235,143	8,629
155	8,534	63,019	170,410	191,990	8,632

Продолжительность сушки, мин ---Расчет о Эксперимент

Рис. 2. Кривая сушки фильтрата пивной дробины при температуре сушильного агента 60 °С

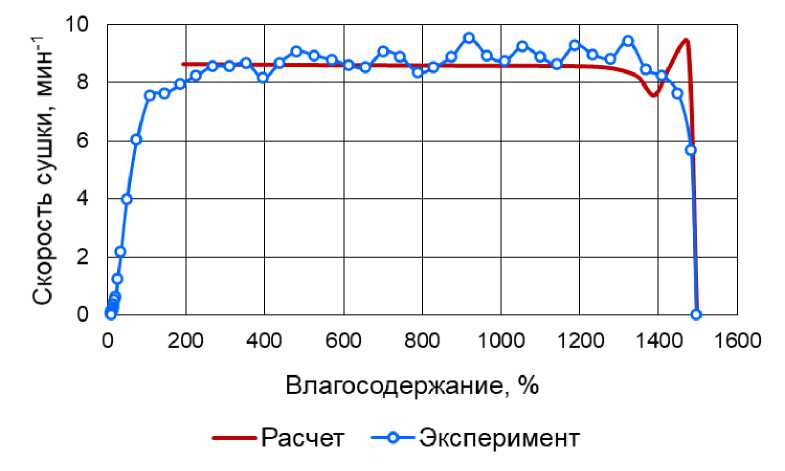
Рис. 3. Кривая скорости сушки фильтрата пивной дробины при температуре сушильного агента 60 °С

Анализ рисунков 2, 3 показывает, что период прогрева составляет порядка 15 мин, скорость сушки фильтрата пивной дробины в период удаления свободной влаги достигает в среднем 9 мин^-1. Сплошной линией приведены расчетные данные, полученные по разработанной математической модели нестационарного процесса испарения жидких растворов с инертной поверхности при вынужденной конвекции, изложенной в [5]. Данная модель применена для описания периода прогрева материала и удаления свободной влаги из материала (первого периода сушки). Параметр идентификации составил k = 2, что больше, чем при исследовании кинетики испарения эталонной жидкости (дистиллированной воды), для которой k = 0,75 [6]. Данное расхождение можно объяснить тем, что при испарении чистой жидкости в конце процесса испарения поверхность массообмена уменьшается, а при сушке жидкого раствора поверхность массообмена первоначально увеличивается за счет пористости твердого вещества, а затем, по мере его высушивания, уменьшается. Фильтрат пивной дробины по существу является жидкостью и переходит в твердое состояние в процессе сушки.

Наблюдаемый на рисунке 3 скачок скорости сушки на стыке между периодом прогрева материала и периодом удаления свободной влаги свидетельствует о погрешности или, возможно, сложности описания точки перехода. Однако описание практически прямой линией периода удаления свободной влаги является достоинством модели, представляющей собой совокупность нелинейных уравнений. Относительное отклонение расчетных значений влагосодержа-ний от экспериментальных не превышает 4 %. Для описания кинетики сушки при удалении связанной влаги необходимо учесть адсорбционный эффект взаимодействия влаги с твердым веществом.

Выводы. Содержание твердых веществ в фильтрате пивной дробины ООО «Майкопское пиво», полученного путем отжима сырой пивной дробины, составляет 6,26 %. Математическая модель нестационарного процесса испарения жидких растворов с инертной поверхности при вынужденной конвекции адекватно описывает экспериментальные данные кинетики сушки фильтрата пивной дробины. Относительное отклонение расчетных данных от экспериментальных не превышает 4 %. Для описания кинетики сушки при удалении связанной влаги рекомендовано в математической модели учесть адсорбционный эффект взаимодействия влаги с твердым веществом.

Список литературы Применение математической модели нестационарного испарения жидких растворов для описания кинетики сушки фильтрата пивной дробины

Колпакчи А.П., Голикова Н.В., Андреева О.П. Вторичные материальные ресурсы пивова-рения. М.: Агропромиздат, 1986. 160 с.
Патент РФ на изобретение № 2215426. Способ переработки отходов пивоваренно-го производства / А.Д. Рекало, А.В. Иванов; заявка № 2002102187/13 от 29.01.2002; опубл. 10.11.2003, Бюл. № 31.
Петров С.М., Филатов С.Л., Пивнова Е.П. и др. К вопросу о способах утилизации пивной дробины // Пиво и напитки. 2014. № 6. С. 32–37.
Баланов П.Е. Технология бродильных про-изводств: учеб.-метод. пособие. СПб.: Изд-во НИУ ИТМО; ИХиБТ, 2013. 65 с.
Korotkova T.G., Konstantinov Eu.N., Danilchenko A.S. et al. Development and Identification of a Mathematical Model for Nonstationary Heat and Mass Transfer in the Water/Air System with Forced Convection // International Journal of Applied Engineering Research. 2016. Vol. 11, № 18. pp. 9551–9556.
Korotkova T.G., Danilchenko A.S., Sedoy Yu.N. Evaporation Rate of Water from Glass Surface under Natural and Forced Convection // Inter-national Journal of Mechanical and Production Engineering Research and Development. 2019. Vol. 9. Issue 4. pp. 955-962. DOI: 10.24247/ijmperdaug201997.

Еще