Применение метода проекции градиента к численному решению совместной системы уравнений Стокса и уравнений Рейнольдса

Характерной особенностью строения верхней оболочки Земли (литосферы) является ее ярко выраженная горизонтально слоистая по вязкости и плотности приповерхностная структура. Поэтому в качестве реологической модели литосферы часто используют вязкую среду, на поверхности которой расположен тонкий пограничный слой [1]. Численное моделирование движения такой среды с помощью однородной во всей расчетной области системы уравнений связано со значительными вычислительными затратами, так как для достижения достаточной точности приближенного решения пространственный шаг дискретизации следует выбирать много меньше толщины погранслоя.

Для того чтобы обойти указанные затруднения, используются так называемые совместные модели (“coupling models” в англоязычной литературе), соединяющие в себе упрощенные уравнения в погранслойном приближении с более общими уравнениями вязкой жидкости. Хотя численное решение этих уравнений по отдельности не вызывает особых сложностей, однако в дальнейшем возникает проблема их сопряжения. В настоящее время для этой цели, как правило, применяются многошаговые итерационные процедуры, с помощью которых достигается выполнение условий непрерывности полей скоростей и напряжений в узлах расчетной сетки, расположенных на границе сопряжения областей с разнородными вязкими течениями [2]. Однако использование таких процедур также требует существенных вычислительных затрат.

В данной работе предлагается совместная численная модель многослойного пласта переменной толщины, расположенного на вязком слое. Для описания течения в этом пласте используются уравнения смазки (уравнения Рейнольдса), а для течения в вязком слое — уравнения Стокса. Разработан метод сопряжения разнородных уравнений, не использующий каких-либо итерационных процедур. Проведено сравнение численных результатов с аналитическим решением.

2.    Система уравнений. Вариационная постановка задачи Рис. 1. Общая схема расчетной области

Представим расчетную область как слой вязкой несжимаемой жидкости с плотностью р и вязкостью ц , на поверхности которого расположен тонкий пласт, состоящий из N слоев. Обозначим через Z_k ( к = 0, N ) границы многослойного пласта. Так как течение жидкости имеет субгоризонтальный характер не только в самом пласте, но и в окрестности верхней границы подстилающего его вязкого слоя, поставим ниже границы Z_N (на расстоянии порядка Z ₀ - Z_N ) фиктивную горизонтальную границу Z N +1 , которая разделит расчетную область на верхнюю — D ₁ , и нижнюю — D ₂ , подобласти (см. общую схему, Рис. 1).

Для описания движения жидкости в каждом слое подобласти D ₁ воспользуемся упрощенными уравнениями смазки (уравнениями Рейнольдса)

Р ,1 =Ц k u 122 ,  Р ,2 =^-Р k g  ^{( к} = 1, N ⁺ 1)

и условием несжимаемости

U , i = 0,                                                           (2)

где рk и цк — плотности и коэффициенты вязкости жидкости в слоях пласта (причем рN+1 = р и цN+1 = ц ); g — ускорение силы тяжести; ui — компоненты скорости; p — давление. Запятая в индексах обозначает дифференцирование u122 = 52u1 /дx2 , uu =^(5ui /5xi).

i =1

Уравнения (1), (2) получены из уравнений Навье–Стокса при следующих предположениях:

– характерный горизонтальный масштаб возмущений много больше вертикального;

– негидростатические напряжения много меньше гидростатического давления;

– плотность не убывает с глубиной.

На границах раздела слоев зададим следующие условия:

• - на поверхности x ₂ = Z ₀ отсутствуют внешние напряжения

p = 0,      ц 1 u ₁₂ = 0;                                             (3)

- на границах раздела слоев x ₂ = Z_k ( к = 1, N ) скорости и напряжения непрерывны

[ U 1 ] - = 0,      [ p ] - = 0,      [ц U 1,2 ] - = 0,

где символ [ ] + означает скачок по координате x ₂ соответствующей функции на границе раздела слоев.

Пусть на боковых границах каждого слоя подобласти D ₁ выполняются условия непроницаемой стенки:

u1,2 = 0.(5)

Для описания движения жидкости в подобласти D ₂ используем уравнения Стокса:

[ц(ии + ujJ], - p,i-р g32 = 0,(6)

где 3 j — символ Кронекера. Скорости в (6) также удовлетворяют условию несжимаемости (2).

На границе Z N _{+ 1} условия непрерывности полей скоростей и напряжений принимают следующий вид:

[ u,.]+= 0,     ц( u1,2 + u 2,1 )| ZN+1_о =ц u1,2 ZN+1 +о,     - p + 2ц u 2,2 ZN+1-0 =- p\z„+1 +0.

После решения (1), (2) с краевыми условиями (3), (4) и подстановки результата в (7) получим:

[ u i ] - = ⁰,

^Ц ( ^и12 + u 2,1 )|

Ni

I Z N + i -0

■ ^ 1 ^p 1 Zi ,1 ⁺ ^ ^(p k   ^P k -1 ) Z k ,1 l⁽ Zi    Z i +1 ) ’

N

■ p + 2 ц u 2,2

'^Pi ( Zi - Zi+1 }

i =1

На нижней и боковых границах подобласти D ₂ зададим условие гладкого контакта:

Uj n_} = 0,

где n _j — направляющие косинусы нормали к границе расчетной области.

Для численного решения задачи перейдем к эквивалентной вариационной формулировке уравнений (6). Для этого умножим их скалярно на соленоидальное поле v_i и преобразуем по формуле Остроградского– Гаусса. Используя краевые условия (8), (9), запишем следующее вариационное уравнение:

J ⁽ ui , vi ) = C ⁽ ui , v i) ^- F 1 ⁽ V ) ^- F 2 ⁽ v i) = ⁰ ,

где

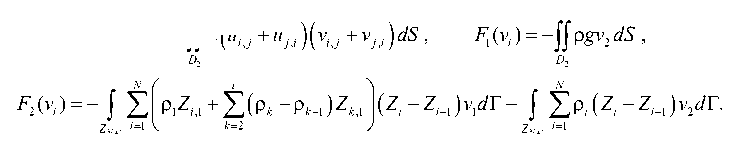
C ( u i ., v i ) = jj ц ( U i , j + U j , i )( V i j + v^ ) dS ,       F ( V i ) = - Jj p gv 2 dS

N

N

Искомое поле скоростей является минимумом функционала J ( u_i , u_i ) на пространстве соленоидальных полей, удовлетворяющих условию несжимаемости (2). Для его определения применим модифицированный метод конечных элементов в сочетании с методом проекции градиента [3].

3.    Аналитическое решение и его исследование

В качестве тестового примера построено аналитическое решение для модели с однослойным пластом в предположении малых деформаций границ слоев. Для описания течения в верхней ( D ₁ ) и нижней ( D ₂ ) подобластях использовались уравнения Стокса (6).

Для приведения уравнений к безразмерному виду определим масштабы длины, плотности, вязкости, давления, скорости и времени: L = 400 - 10 3 м, р ₀ = 3000 кг^м^-3, ц ₀ = 10²² Па^с, p ₀ = p ₀ gL , u ₀ = 0,001 -p ₀ gL -ц - ¹ , t ₀ = L - u - ¹ . Параметры слоев выбирались следующими: H ₁ = 0,1, H ₂ = 0,9 — толщины верхнего и нижнего слоев; р ₁ = 1, р ₂ = 1,1 и ц ₁ = 1, ц ₂ = 1 — плотности и вязкости верхнего и нижнего слоев соответственно. В начальный момент времени на границах Z ₀ и Z ₁ задавались малые деформации z ₁₀ и z ₂₀ .

С помощью преобразований Фурье и Лапласа (см., например, [4]) получим аналитическое решение для скоростей:

U ₁ = ( A₁₁ exp ( - 0,388401 1 ) + A ₁₂ exp ( - 0,000484 1 ) ) sin x₁ , U 2 = ( A ₂₁ exp ( - 0,388401 1 ) + A ₂₂ exp ( - 0,000484 1 ) ) cos x ₁ ,

где коэфициенты A_ij вычисляются следующим образом: – в верхнем слое:

A ₁₁ = ( ( 0,56494 x ₂ + 0,11252 ) z₁₀ + ( 0,00983 + 0,04938 x ₂ ) z ₂₀ ) ch x ₂ + + ( ( 0,53288 - 1,04884 x ₂ ) z ₁₀ + ( - 0,09167 x ₂ + 0,04657 ) z ₂₀ ) sh x ₂ ,

A 12 = ( ( 0,119632 x ₂ - 0,112523 ) z ₁₀ + ( 0,128745 - 0,136879 x ₂ ) z ₂₀ ) ch x ₂ + + ( ( 0,15170 - 0,15711 x ₂ ) z ₁₀ + ( 0,17976 x ₂ - 0,17357 ) z ₂₀ ) sh x ₂ , A ₂₁ = ( ( 1,04884 x ₂ + 0,03206 ) z ₁₀ + ( 0,00280 + 0,09167 x ₂ ) z ₂₀ ) ch x ₂ + + ( ( - 1,16136 - 0,564945 x ₂ ) z ₁₀ + ( - 0,049376 x ₂ - 0,101502 ) z ₂₀ ) sh x ₂ , A ₂₂ = ( ( 0,15711 x ₂ - 0,03206 ) z ₁₀ + ( 0,03668 - 0,17976 x ₂ ) z ₂₀ ) ch x ₂ + + ( ( - 0,04459 - 0,11963 x ₂ ) z ₁₀ + ( 0,13688 x ₂ + 0,05102 ) z ₂₀ ) sh x ₂ ;

– в нижнем слое:

A 11 = ( ( 0,060303 z ₂₀ + 0,68997 z ₁₀ ) x ₂ ) ch x ₂ + ( ( - 1,2234 z ₁₀ - 0,10692 z ₂₀ ) x ₂ + 0,06030 z ₂₀ + 0,68997 z ₁₀ ) sh x ₂ , A ₁₂ = ( 0,00617 z ₂₀ - 0,00539 z ₁₀ ) x ₂ ch x ₂ + ( ( 0,01743 z ₁₀ - 0,01995 z ₂₀ ) x ₂ + 0,00617 z ₂₀ - 0,00539 z ₁₀ ) sh x ₂ , A 21 = ( 0,10692 z ₂₀ + 1,2234 z ₁₀ ) x ₂ ch x ₂ + ( ( - 0,68997 z ₁₀ - 0,060303 z ₂₀ ) x ₂ - 1,2234 z ₁₀ - 0,10692 z ₂₀ ) sh x ₂ , A 22 = ( 0,01995 z ₂₀ - 0,01743 z ₁₀ ) x ₂ ch x ₂ + ( (0,00539 z ₁₀ - 0,00617 z ₂₀ ) x ₂ - 0,01995 z ₂₀ + 0,01743 z ₁₀ ) sh x ₂ .

Деформации границ слоев рассчитываются по формулам:

z 1 = ( B 11 exp ( - 0,388401 t ) + B ₁₂ exp ( - 0,000484 t ) ) cos x 1 , z ₂ = ( B ₂₁ exp ( - 0,388401 1 ) + B ₂₂ exp ( - 0,000484 1 ) ) cos x 1 ,

где    B 11 = 0,92903 z ₁₀ + 0,08120 z ₂₀ ,       B ₁₂ =- 0,08120 z ₂₀ + 0,07097 z ₁₀ ,       B ₂₁ = 0,07097 z ₂₀ + 0,81197 z ₁₀ ,

B ₂₂ = 0,92903 z ₂₀ - 0,81197 z ₁₀ .

Из формул (11), (12) следует, что характерной особенностью рассматриваемого процесса является наличие двух режимов эволюции: интенсивное изменение за относительно короткий начальный промежуток времени (так называемый временной пограничный слой) и квазистационарная стадия (за большие промежутки времени решение изменяется весьма незначительно). Так как на больших временах ( t ~ 1000 ) быстро убывающие экспоненты в решении становятся пренебрежимо малыми, эволюция границ обуславливается лишь медленно убывающими компонентами. Так как отношения коэффициентов при них в (12) почти равны: ( B ₁₂ / B ₂₂ )|_A_₀ ~- 0,0873996, ( B ₁₂ / B ₂₂ )|_A_₀ ~- 0,0873996, отношение деформаций z 1 /z ₂ на больших временах остается практически неизменным при любых комбинациях задаваемых начальных возмущений z ₁₀ и z ₂₀ .

На рисунке 2 приводятся поля скоростей в моменты времени t = 0 и t = 1000. Начальные возмущения границ выбирались такими, чтобы выполнялось условие гидростатического равновесия:

^р 1 ^z 10 ^+(р 2 ^-р 1 ) ^z 20 = ^{0.                                             (13)}

Из рисунка видны существенные отличия полей скоростей в начальный момент времени и на больших временах.

"1,0

"0,1

-0,2

-0,3

-0,4

-0,5

-0,6

-0,7

-0,8

-0,9

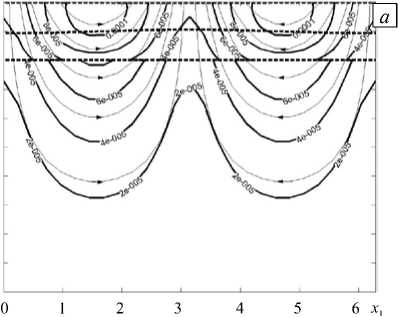
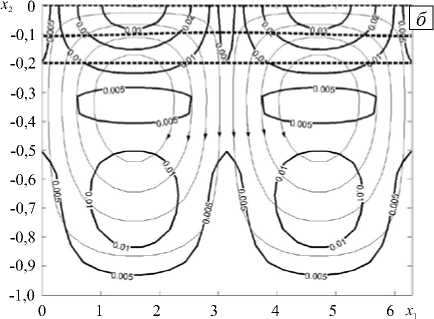
Рис. 2. Эволюция поля скоростей: в начальный момент времени ( а ); на больших временах t = 1000 ( б ); жирные сполошные линии – модуль скорости, тонкие линии – линии тока, жирные пунктирные линии – границы слоев многослойного пласта

5.    Численные результаты

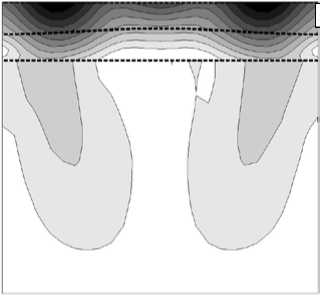
При вычислении приближенного решения возмущения границ слоев в начальный момент времени также выбирались удовлетворяющими условию (13). Найденное в нижней подобласти D ₂ поле скоростей использовалось как краевое условие на границе сопряжения Z N +1 при расчете скоростей в верхней подобласти D ₁ с помощью уравнений (1), (2) с условиями (3), (4). На рисунке 3 показана величина погрешности численного решения для поля скоростей на малых и больших временах, которая вычислялась по формуле:

n=м=0 - u i l/max НJ.

В начальный момент максимальное значение погрешности nmax ~ 0,18 достигается вблизи поверхности и обусловлавливается тем, что для описания течения жидкости в верхней подобласти используются упрощенные уравнения вязкой жидкости (1), (2). Достаточно хорошее приближение к точному решению (11) имеет место в окрестности границы сопряжения подобластей: nmax ~ 0,06 • Численная аппроксимация поля скоростей на больших временах (Рис. 3, б) значительно отклоняется от точного решения (11): максимальное значение погрешности составляет nmax ~ 0,18 ; максимальная погрешность на границе сопряжения также достаточно велика: nmax ~ 0,14.

0       1       2       3        4       5        6 Л-,

-0,02

-0,04

-0,06

-0,08

-0.10

-0,12

-0.14

-0,16

-0,18

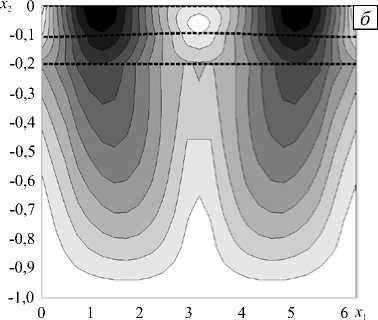
Рис. 3. Невязка численного решения для поля скоростей в начальный момент времени ( а ); на больших временах ( б )

5.    Асимптотическое условие на больших временах

В этом разделе предлагается способ улучшения аппроксимации поля скоростей на больших временах. Заметим, что в случае отсутствия перепада плотности между пластом и подстилающим вязким слоем точное аналитическое решение для поля скоростей имеет следующий вид:

U 1 = ( ( - 1,206 x ₂ + 0,6846 ) sh x ₂ + 0,6846 z ch x ₂ ) z ₁₀ exp ( - 0,36087 t ) sin x 1 , U ₂ = ( ( - 1,206 - 0,6846 x ₂ ) x ₂ sh x ₂ + 1,206 z ch x ₂ ) z ₁₀ exp ( - 0,36087 t ) cos x 1 .

Следовательно, изменение режима эволюции на больших временах полностью связано с неравенством плотностей пласта и вязкого слоя. Для того чтобы улучшить точность приближения, необходимо исследовать особенности эволюции этого пласта.

Решая (1) с краевыми условиями (3), (4) и подставляя полученное решение в кинематическое условие отсутствия перетекания массы через границу, имеем:

u ₂ ( x 1 , Z i , t ) - Z i ,1 u 1 ( x 1 , Z i , t ) - Z i , _t = 0    ( i = 1, N ).                                   (16)

После некоторых преобразований получим следующие безразмерные уравнения относительно Z_i ( x ₁ , t ):

^Z 1, t = ( ^{( y} j^Aj^Zj ,1 )   ^{( Z}i   ^ZN +1 ) u 1 ⁽ x 1 , ^ZN +1 , ^L ) ) 1 ⁺ u 2 ⁽ x 1 , ^ZN +1 , ^L )      ⁽ i = 1, ^N ),

h где4 = Aji=^hi^hj^        -—-^-  (i< j,  i,j = 1,2 ); h= Zi+1 -Zi;  Yi = 1;  Y2 = (p2-Pi)/po ;

^l = i m = j k = j ц k ( 1 + о jk + o j )

8 j — символ Кронекера. Так как безразмерная разность плотностей коры и мантии Земли и других твердых планет составляет у ₂ ~ 0,1, эту величину можно считать малым параметром.

Проведем асимптотический анализ системы (17). Подробное изложение применяемого асимптотического метода приводится в работе [5]. В результате было получено следующее асимптотическое уравнение на больших временах:

( У j A j Z j ,1 )_д + Z n +i u i,i ( x i , Z n +i , t ) + u 2 ( x i , Z n +i , t ) = 0.                                 (18)

Используем уравнение (18), связывающее положения границ слоев и скорости на границе сопряжения на больших временах и не зависящее от предыстории течения, в качестве дополнительного ограничения на минимизируемый функционал J ( u_i , u_i ).

Пусть X m ( l = 1, 2 L + 1, m = 1, 2 M + 1) — узлы разностной сетки, причем границе Z N _{+ i} соответствуют узлы с индексом m = 1 . Аналогично методу, примененному в [3], заменим полученное условие интегральным эквивалентом:

_г 1 m + 2

x ₁

j ( ( A _ii Z _ц + A ₁₂ Z ₂₁ - u ₁ Z ₃ )_t + u ₂ ) dx = 0 ( m = 1,3,...,2 M - 1);

x11m                                                            , используя сеточную функцию тока Slm при вычислении интеграла (19), найдем:

x ¹ m

( A 11 Z 1,1 + A 12 Z 2,1 - U i Z 3 )| x i m  - S^{1 m + 2} + S^{1 m} = 0  ( m = 1, 3, . , 2 M - 1).

Учитывая, что S ¹¹ = 0 и u¹ = 0, и заменяя в (20) производные Z_i1 центральными разностями, получим систему сеточных уравнений, которая легко решается относительно u ₁ ^{1 m} .

гу 1 m +1   /у1 m -1                    im\m +1   /yi m -1

Z i - Z i             Z 2 - Z 2

11 lx = x1 m    1 m+1     1 m-1 + ^21 lx = x1 m    1 m+11

11  Xi   - Xi           11  Xi

10    12         12 M     12 M -2

Xi Xi ,        Xi

- u i ^mZ 3 ^m - S ^{1 m} = 0   ( m = 1,3,

2 M - 1);

Так как систему ограничений (21) можно явно разрешить относительно значений u ₁ ^{1 n} , условная минимизация функционала J ( u_i , u_i ) легко осуществляется методом проекции градиента [3].

На рисунке 6 показаны графики горизонтальной (кривая 1 ) и вертикальной (кривая 2 ) составляющих

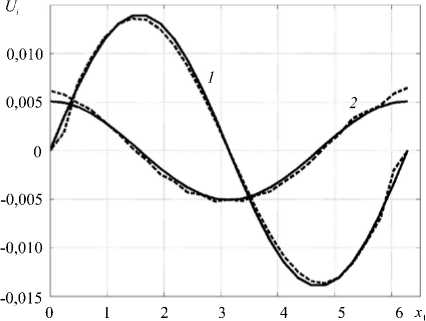
Рис. 6. Графики горизонтальной (кривая 1 ) и вертикальной ( 2 ) составляющих скорости движения жидкости на границе сопряжения областей с разными свойствами на больших временах

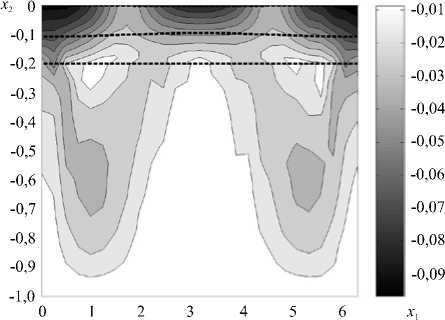
Рис. 7. Невязка численного решения с дополнительным условием на больших временах

скорости движения жидкости на границе сопряжения области неоднородности и вязкого слоя в момент времени t = 1000. Сплошная линия соответствует точному, а пунктирная — численному решению.

Рисунок 7 содержит невязку численного решения с дополнительным условием (21) в момент времени t = 1000. Максимальная погрешность численного решения, вычисляемая по формуле (14), составляет n max = 0,1, максимальная погрешность на границе сопряжения — n max ~ 0,05 ■

Большинство разработанных совместных моделей [2] предварительно вычисляют поле скоростей с большой погрешностью, используя краевое условие внешней нагрузки (8), а затем с помощью итерационных процедур уточняют это решение. Дополнительное условие (18) позволяет сразу получить численное решение с хорошей точностью без какого-либо итерационного уточнения.

6.    Заключение

Разработана совместная численная модель тонкого многослойного пласта переменной мощности, лежащего на вязком слое, которая соединяет в себе уравнения Рейнольдса с уравнениями Стокса. Получено аналитическое решение для модели с однослойным пластом и проведено его исследование. Анализ решения выявил существенные различия режимов эволюции поля скоростей на малых и больших временах. Сравнение численного решения с аналитическим показало хорошее приближение на малых временах, но значительное расхождение на больших временах эволюции. С помощью метода малого параметра получено асимптотическое уравнение, которое использовалось в качестве дополнительного ограничения на искомое решение. Для численной реализации этого условия использовался метод проекции градиента. Результаты моделирования подтвердили, что использование этого ограничения позволяет получить хорошее приближение для скоростей на больших временах без использования каких-либо уточняющих итерационных процедур.