Применение методов математического моделирования в оптимизационном проектировании технологических процессов производства пищевых продуктов

Многообразие состава и свойств пищевых продуктов, применяемых в отрасли организации питания, используемых в кулинарной практике, многообразие рецептур и разнотипность оборудования обусловливают многочисленность способов тепловой обработки и широкие диапазоны ее режимов. При этом от способа, режима и продолжительности обработки зависят санитарная безопасность, органолептические показатели, пищевая и биологическая ценность, сохранность ценных биологически активных компонентов, а также технологические потери продукции.

Одним из перспективных направлений развития пищевой индустрии в повышении сохранности свойств термолабильных ингредиентов является применение щадящей термической обработки сырья с предварительной вакуумной упаковкой в полимерную термоустойчивую пленку – технология Sous-Vidе или LТ-LT-обработка («low-temperature – long-time») [1–9]. Данный метод приготовления пищи был разработан и применен в середине 1970-x годов шеф-поваром Джорджем Пралюсом (Georges Pralus) при приготовлении паштета из гусиной печени фуа-гра. В настоящее время данная технология находит свое применение в сегменте корпоративного питания, в фаст-фудах, в заготовочных цехах крупных ресторанов. В то же время процесс Sous-Vidе обработки является нестационарным, характеризуется комплексом термохимических и биологических превращений пищевых систем, оптимизация которых может быть осуществлена только с учетом динамики температурных полей на основе решения задачи нестационарной теплопроводности.

Материалы и методы

При решении поставленной задачи по оптимизации процесса щадящей тепловой обработки пищевых систем применено дифференциальное уравнение нестационарной теплопроводности:

at   Да ² 1   a²1   а ² 1 )

— = k\—г + —г + —? ,      (1)

ат (ax2  y2   az2 J где t – температура, °С; τ – продолжительность, с; k – коэффициент температуропроводности продукта, м2/с.

Дополняя (1) начальными и граничными условиями, можно получить решения задачи нестационарной теплопроводности в аналитическом виде для тел простейшей формы, например, неограниченной пластины, неограниченного цилиндра, шара или численными методами для тел произвольной формы [10].

В дифференциальном уравнении (1) параболического типа предполагается, что теплота распространяется с бесконечной скоростью. В [11] рассмотрен подход, основанный на конечной скорости распространения теплоты, что характерно для большей части пищевых продуктов, который позволил путем введения понятия «температурный фронт» и заменой производной от температуры по времени в возмущенной области ее средним (по протяженности возмущенной области) значением свести уравнение в частных производных для одномерной области к обыкновенному дифференциальному уравнению. Такое модельное представление о распространении теплоты позволило в аналитическом виде анализировать проблемы, возникающие при тепловой обработке пищевых продуктов простейшей геометрической формы. Тем не менее, как в первом, так и во втором случаях для проведения конкретных расчетов необходимо иметь справочные данные по теплофизическим свойствам продуктов, подвергаемых термообработке.

Вакуум-упакованная поликомпонентная пищевая система, состоящая из 16% масс. моркови, 12,5% масс. лука репчатого, 25,5% мас. картофеля, 20,0% масс. свеклы столовой, 26,0% масс. функциональной растительной композиции на основе продуктов глубокой комплексной переработки растительного сырья (муки зародышей пшеницы, семян амаранта, тыквы, льна, биологически активных добавок к пище «Селексен», «Флавоцен») [12, 13], представляла собой геометрическую фигуру, которую можно приближенно представить в виде пересечения прямоугольного параллелепипеда, длина и ширина основания которого равны a = 140 мм и b = 105 мм, с эллипсоидом вращения, у которого полуоси равны a , b и c = 3,5 мм. Углы прямоугольного параллелепипеда скруглены радиусом R = 15 мм (рисунок 1).

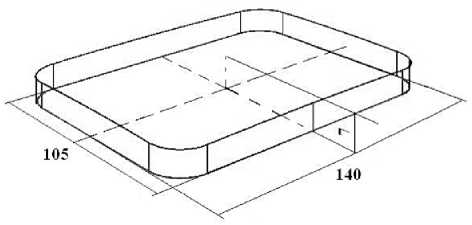
Рисунок 1. Схематическое изображение исследуемой вакуум-упакованной поликомпонентной пищевой системы

Figure 1. Schematic representation of the investigated vacuum-packaged multicomponent food system

Результаты и обсуждение

Для расчета теплофизических характеристик поликомпонентной пищевой системы примем, что объем пищевой системы равен сумме объемов составляющих ее компонентов, тогда плотность смеси можно рассчитать по формуле [14]

─ если все компоненты пищевой системы расположены по направлению теплового потока, то максимальная величина теплопроводности системы будет определять как

' . = £ —». ;

- = 1

-= tA , p    i = 1 p i

где p - плотность пищевой системы, кг/м3; x – массовая доля i-го компонента, имеющего плотность p ; n - число компонентов в пищевой системе.

Удельную теплоемкость пищевой системы рассчитаем по зависимости c =

1 v — t г^-, p -=1 ki где Xi, ki - теплопроводность, Вт /(м • К), и температуропроводность, м2/с, i-го компонента пищевой системы; » - объемная доля i-го компонента пищевой системы, которую определим по соотношению

x

»- = p-

nxi и p-

Экстремальные значения теплопроводности пищевой системы, состоящей из n компонентов, с использованием метода электроаналогии, можно найти из следующих предположений:

─ минимальное значение теплопроводности пищевой системы соответствует случаю, когда отдельные частицы имеют расположение, перпендикулярное направлению распространения теплоты (градиенту температуры), что влечет за собой применение соотношения

— = У » ". X min    t ! X -

Для теплофизических расчетов теплопроводность пищевой системы определим как среднеарифметическое значение найденных экстремальных величин

X +x

max     min min                     .

Входящую в уравнение (1) температуропроводность пищевой системы рассчитаем по формуле k =—. pc

Результаты вычислений теплофизических характеристик поликомпонентной пищевой системы, подвергнутой Sous-Vidе обработке, представлены в таблице 1.

Таблица 1.

Теплофизические свойства поликомпонентной пищевой системы, подвергнутой Sous-Vide обработке

Table 1.

Thermophysical properties of a multicomponent food system subjected to Sous-vide processing

Физическая величина | Physical quantity	Температура в центре продукта, °С / продолжительность LT-обработки, мин | The temperature in the center of the product, ° C / duration of LT processing, min
	20 °С/0 мин	65 °С /11 мин	85 °С /25 мин	89 °С /42 мин
ρ , кг/м3	972,5	1009,3	1026,4	1039,5
c , Вт/ кг · К	3530,6	3308,8	3129,5	2939,2
λ , кг/ м · К	0,4744	0,4408	0,4038	0,3706
k , м2/ с · 107	1,381	1,326	1,257	1,213

Динамика температурного поля в пищевой системе, рассчитываемая с использованием уравнения (1), в значительной степени определяется граничными условиями. С учетом того что термообработка образцов проводилась горячим воздухом с температурой t ∞ = 95°С, для которого коэффициенты теплоотдачи достаточно малы, приняты граничные условия 3-го рода, определяемые уравнением

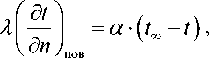
где X - теплопроводность продукта, Вт / (м-К); n - нормаль к поверхности образца; а - коэффициент теплоотдачи от воздуха к поверхности материала, Вт/(м²·К).

Так как испытуемый образец находится внутри полимерной тары, то необходимо оценить ее термическое сопротивление. Упаковочные пленки имеют толщину порядка 100 мкм, а по имеющимся данным [15] ее температуропроводность имеет примерно такую же величину, что и у исследуемой пищевой системы – (11 ÷ 15) · 10-8 м2/с, в связи с этим ее влияние на поле температур внутри продукта можно не учитывать.

Верхняя поверхность образца имеет малую кривизну, поэтому расчет коэффициента теплоотдачи в (3) будем вести по критериальным уравнениям как в случае обтекания теплоносителем плоской поверхности [14]. Для выбора расчетной формулы необходимо рассчитать число Рейнольдса

Re = ud P ,

P где u - скорость воздуха, м/с; ц - динамическая вязкость воздуха, Па•с; р - плотность воздуха, кг/м3; d – длина пути потока вдоль теплообменной поверхности, м.

Так как расположение образца относительно направления движения воздуха может быть произвольным, а образец не имеет полной симметрии, то расчет а будем вести для двух характерных направлений – вдоль большой оси эллипсоида вращения и в поперечном направлении.

Длина дуги эллипса, получаемого при сечении образца вертикальной плоскостью, проходящей через его большую ось, определяется по формуле [16]

t ₂

l_x = a f ^/1 - e_x 2 cost dt , (4) t ₁

где e – эксцентриситет эллипса, определяемый выражением ei = ^1 — b?, 6 G[0,1).          (5)

Для принятой геометрии образца t_x = П 3, а t ₂ = 2 П 3.

После подстановки принятых значений, а = 140 мм, b = 105 мм в соотношения (4) и (5), используя пакет символьной математики Maple для взятия эллиптического интеграла в (4), получим значение l 1 = 145 мм.

Для поперечного направления расчетные формулы примут вид t2

l2 = bf ^/1 - e2 costdt, t1

где e2

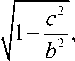
а t 1 = П 3, а t ₂ = 2 П 3 •

Для значения c = 3,5 мм получили значение длины дуги эллипса, равное l 2 = 109 мм.

Если рассматривать влажный воздух как бинарную смесь сухого воздуха и водяного пара, то его плотность можно рассчитать из соотношения [17, 18]

=   Pn(1 + x)

^P  ( x + M n / M _CB ) ,

где – молярные массы водяного пара и сухого воздуха, равные соответственно М п = 18,016 кг/кмоль и М св = 28,96 кг/кмоль; р п - плотность водяного пара, кг/м³; x – влагосодержание паровоздушной смеси.

Плотность водяного пара определяют из уравнения состояния

Р = Mp

RT где R = 8314 Дж/(кмоль · К) – универсальная газовая постоянная; p – давление, которое примем равным атмосферному; Па, Т – абсолютная температура, К.

Влагосодержание воздуха при его известной относительной влажности ф находят по зависимости [17, 18]

x =

M ф ——

M

СВ

(plpt) AA exp [-B (1 -11)+C (1 -t)]- ф ’ где pt= 610,8 Па – давление насыщенных паров воды при То = 273,15 К; t = T/Tt - относительная температура; А, В, С – коэффициенты, численные значения которых [15, 16] равны

А = 9,248; В = 27,098; С = 2,005.

Динамическую вязкость влажного воздуха в зависимости от его влагосодержания x можно найти с использованием формулы Уилки [16, 17]

P n ^x       ,        P cb

Если использовать безразмерную температуру t = T/T0, где Т — температура набегающего потока воздуха, К, то р = 2,91-10—513/2/(t + 2,38),      (8)

р = 2,41 - 10 — 5 1 ^3/2/( t + 0,41).      (9)

При температуре греющего воздуха t∞= 100°С и его относительной влажности Ф= 0,85 для давления p = 101325 Па получены значения плотности пара и паросодержания воздуха, равные соответственно рП = 0,588 кг/м3 и x = 3,577. Тогда плотность влажного воздуха по (6) примет значение р = 0,642 кг/м3.

Динамическая вязкость водяного пара и сухого воздуха согласно уравнениям (8) и (9) составляет µ п = 1,24·10^-5 Па·с и µ св =2,17·10^-5 Па·с соответственно, динамическая вязкость влажного воздуха по уравнению (7) равна р = 1,38 • 10^-5 Па^с.

При скорости воздушного потока u = 1,2 м/с число Рейнольдса при продольном обтекании верхней поверхности образца будет

Re

в

1,2 - 0,145 - 0,642

1,38 - 10 ^{- 5}

= 8109.

Пренебрегая кривизной, теплоотдачу от верхней поверхности образца при Re < 5·105 будем рассчитывать как для плоской поверхности по формуле [14]

Nu1в = 0,664 · Rе1в1/2 ·Рr1\3, где Pr – число Прандтля для воздуха при температуре набегающего потока, которое рассчитывается по соотношению

Pr = V = р , к л

где v - кинетическая вязкость, м²/с; р с - объемная теплоемкость, Дж/ м³-К; Л - теплопроводность, Вт/м·К влажного воздуха.

Так как ν = μ/ρ , то с учетом ранее полученных результатов ν = 2,15·10^-5 м²/с. Объемная теплоемкость среды как величина аддитивная находится по формуле [14]

^р п ^с П ⁽ x ^{+ с} СВ / с П ) р с = “7---"----------X ,

( x ⁺ M П / M СВ )

где сп, ссв – удельные изобарные теплоемкости водного пара и сухого воздуха, которые согласно [14] для интервала температур 0–95 °С можно принять равными сп = 1873Дж/кг·К, ссв = 1006 Дж/кг·К.

В результате расчета по (11) получаем ρc = 1079 Дж/ м³·К.

Теплопроводность влажного воздуха является аддитивной величиной и может быть найдена по уравнению [17, 18]

л =

M _П

^Л П x ^{+ Л} СВ ——

П    СВ _{M СВ}

M, x + ——

^M СВ

где ЛП, Лсв - теплопроводности водяного пара и сухого воздуха, определяемые уравнениями

Л п =

0,0595 - t^0,5

2,46 + ——

t

Л св =

0,0347 - t°’⁵

0,454

1 + —--- t

В результате расчетов по (12)–(14) имеем /. , = 0,0248 Вт/(м-К), Л _св = 0,0304 Вт/(м-К), λ = 0,0257 Вт/(м·К).

Таким образом, число Прандтля по (10) будет равно

Pr = 0,902.

Число Нуссельта для верхней поверхности образца при его продольном обтекании воздухом составит Nu в ¹ = 57,8.

При поперечном обтекании образца, когда d = l 2 = 0,109 м, число Рейнольдса равно Rе² в = 6096, а число Нуссельта – Nu в ² = 50,1. Коэффициенты теплоотдачи найдем по формуле

NuЛ что дает следующие результаты а = 57,8-О,0257 = 10,2 Вт/(м2^К), в      0,145

2  50,1- 0,0257  1 1 oT3/z2va а= —---------= 11,8 Вт (м К).

^в       0,109         ^,

Среднее по верхней поверхности образца значение коэффициента теплоотдачи будет равно 0 1 = ( а + а _а ² ) /2 = 11,0 Вт(м ' Ч\).

Для нижней плоской поверхности ва-куум-упакованного продукта при продольном обтекании воздухом d = 0,140 м, Rе¹ н = 7829, Nu 'n = 56,8, 0 1 = 10,4 Вт / (м²тК).

Для поперечного движения воздуха, когда d = 0,105 м, имеем: Rе² н = 5872, Nu² н = 49,2, а „² = 12,0 Вт / (м²^К). Среднее значение коэффициента теплоотдачи - сг н = 11,2 Вт / (м²-К).

Для боковых поверхностей коэффициент теплоотдачи будем считать таким же, как на верхней поверхности.

Для численного интегрирования уравнения нестационарной теплопроводности (1) с граничными условиями третьего рода (2) приведем их к безразмерному виду. При этом необходимо учесть, что для испытуемого объекта размеры по координатным осям различаются больше, чем на порядок. Вследствие этого скорости релаксации температурных возмущений по этим направлениям будут существенным образом отличаться между собой. В связи с этим выбор характерного размера системы l0, определяющего масштаб времени для исследуемого процесса, играет важную роль.

Определим l0 следующим образом i = 4V

0    S, где V - объем тела, м3; 5 - площадь поверхности, м2.

Будем приближенно считать, что вакуум-упакованная пищевая система представляет собой прямоугольный параллелепипед со сторонами а , b , с . Тогда

2 abc

0 ac + bc + ab

Обозначим   c/a = ^ 1 ,  c/b = ^ 2 .

с учетом (15)

l 0         2

с 1 + £ + £ .

Тогда

Пусть масштаб времени равен т = 12 /к • Тогда безразмерное время 0 = т(т ₀ = к т[ 1 ₀².

Пусть безразмерные координаты и температура определяются выражениями:

X = x^a ; Y = y/b; Z = z/c ;

T = (t» - t)/(t» - tо), где  t0

–

начальное значение температуры тела t0, 20 °С.

С учетом принятых обозначений и соотношения (16) уравнение (1) примет вид дT

^d0  ( 1 + £ + ^ 2 ) 2

₆ 82 T + ₆ d j)+У Т 1 (17)

• ¹    д X ²      5 Y ²    5 Z² 1

Начальное условие

Т ( Х, Y, Z, 0) = 1.

Граничные условия

дT ( - 12, Y , Z ,0) ₌

8X д T (12, Y, Z ,0) 8X

– Вi х ·T ( -1\2, Y, Z, θ ),

= Вi х ·T ( 1\2, Y, Z, θ ),

–Вi у ·T ( X,-1\2, Z, θ ),

= Вi у ·T ( X, 1\2, Z θ ),

–Вi zн T ( X, Y, -1\2, θ ),

д T ( X , - 12, Z ,0 ) ₌

д Y дT (X,-12, Z ,0)

д Y dT (X, Y,-1)2,0 0) =

дZ д t ( x , y , z *0)

д Z

= Вi zв T ( X, Y, Z^*, θ ),

Здесь Bi = a al \ , ^Biv = a b/ Л , x      в т              y      в т

Bi ZH = ан h/^t , Bi ze = а в h/Ят ; h - высота прямо- угольного параллелепипеда, эквивалентного по объему образцу, у которого верхняя грань есть эллипсоид вращения (см. уравнение (25)), а нижняя – плоскость.

Если уравнение трехосного эллипсоида вращения, образующего верхнюю грань образца, есть

Z* = c 1 - x 2- - ^ 2 ,         (25)

a ² b ²

то объем верхней половины будет

V в

x ^{2 c}

a

= 4 I

b ² b /2 a /2

j j dxdydz . 00

Так как объем нижней половины равен

Vн = а·b·с,(27)

то весь объем образца составит

V = Vв + Vн,(28)

а высота равновеликого прямоугольного параллелепипеда h = V / (а·b).(29)

Отметим, что уравнение (17) при ^ ^ 0

е п                           дT л д2T и ^ ^ 0 становится одномерным: — = 4—-,

• ²                                 д0    д Z ²

то есть соответствует случаю нагревания (охлаждения) неограниченной пластины.

Вычисления по (29) с учетом (26)–(28), проведенные с использованием пакета символьной математики Maple, дали следующий результат – h = 6,688 мм. Найденное значение эквивалентной высоты прямоугольного параллелепипеда позволило уточнить характерный размер исследуемого объекта l0 путем замены в (5.30) значения c на h/2.

При решении системы дифференциальных уравнений в частных производных (17)–(24) применен математический пакет flехРDЕ, использующий метод конечных элементов для моделирования объектов с распределенными параметрами. В расчетах использована пространственная сетка с числом узлов n = 20000, принята точность вычислений 1·10^-4.

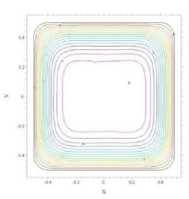
Результаты моделирования, показывающие эволюцию температурных полей на плоскости Z = 0 и на верхней поверхности образца, имеющего форму эллипсоида вращения, представлены на рисунке 2. Проверка адекватности модельных представлений показала, что максимальное отклонение результатов расчета от опытных данных по Sous-Vidе обработке поликомпонент-ной пищевой системы составляет не более 7,2%.

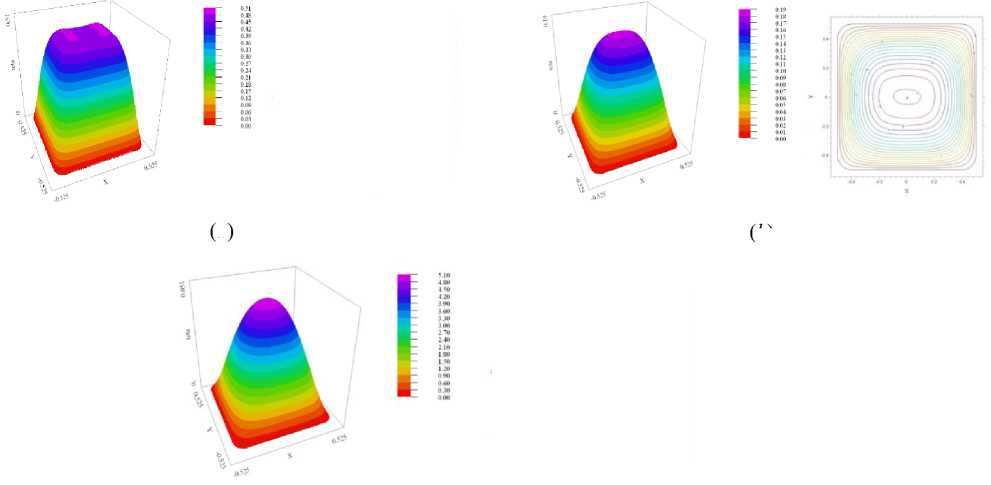
( a )

( b )

( c )

Рисунок 2. Эволюция температурного поля на плоскости Z = 0 (слева) и на верхней поверхности образца (справа) при различной продолжительности Sous-Vide обработки поликомпонентной пищевой системы, мин: а – 11; б – 25; с – 42

Figure 2. Evolution of the temperature field on the Z = 0 plane (left) and on the upper surface of the sample (right) at different Sous-Vide processing times of a multicomponent food system, min: a – 11; b – 25; с – 42

Заключение

Полученная математическая модель позволяет путем вычислительного эксперимента анализировать и оптимизировать режимы Sous-Vidе обработки широкого ассортимента пищевого сырья различной геометрической формы и размера, обладающего разными