Применение методов математической статистики для обработки и анализа результатов педагогического эксперимента

Эксперимент строился на сравнении экспериментальной и контрольной групп студентов специальностей «Энергоснабжение железных дорог (ЭЖД)», «Информационные системы и технологии (ИС)» и «Управление персоналом (УП)», которых распределили на две группы – экспериментальную (109 человек) и контрольную (108 человек). Для определения начального состояния был проведен тест, составленный по курсу школьной программы, показавший отсутствие значимых различий в экспериментальной и контрольной группах. Дальнейшее обучение обеих групп проводилось с применением разных методик: в контрольной группе использовалась традиционная методика, в экспериментальной – инновационный подход к организации самообразовательной деятельности (СОД) на основе матричной модели познавательной деятельности. Данные по контрольному тесту в экспериментальной и контрольной группах приведены в таб. 1.

К у = N . К у е [ 0;1 ]	Здесь Ку – коэффициент усвоения учебной информации отдельным студентом, где N – кол-во правильно выполненных учебных элементов; пр N – общее кол-во учебных элементов в тесте;
К у = NN" , К у е[ 0;1 ]	Здесь Ку – коэффициент усвоения учебной информации отдельным студентом, где N – кол-во правильно выполненных учебных элементов; пр N – общее кол-во учебных элементов в тесте;

Таб. 1. К_у в экспериментальной и контрольной группах

К у Группа	0,2-0,3	0,3-0,4	0,4-0,5	0,5-0,6	0,6-0,7	0,7-0,8	0,8-0,9	0,9-1,0
Экспериментальная группа	0	1	1	5	19	37	32	14
Контрольная группа	2	2	5	10	21	35	24	9

Таб. 2. Основные числовые характеристики случайных величин X и Y

Случайная величина	Выборочная средняя	Выборочная дисперсия	Выборочное среднеквадратичное отклонение
X	xB = 0,763	Dx = 0,013	o x = 0,114
Y	У в = 0,720	Dy = 0,022	о у = 0,149

Начальное состояние

Состояние по итогам контрольного теста

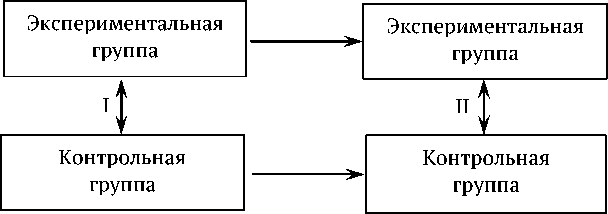
Рис. 1. Структура педагогического эксперимента

Время

Структура педагогического эксперимента ( Михеев, В.И. Моделирование и методы теории измерений в педагогике / В.И.Михеев – Эдиториал УРСС, 2010. – 224 с.; Новиков, Д.А. Статистические методы в педагогических исследованиях / Д.А.Новиков – М.: М3 – Пресс, 2004. – 67с.) представлена на рис. 1.

Алгоритм исследования следующий: 1) На основании сравнения I установлено отсутствие статистически значимого различия между контрольной и экспериментальной группами. 2) Реализовано воздействие на экспериментальную группу, при этом экспериментальная и контрольная группы находились в одинаковых условиях за исключением целенаправленно изменяемых преподавателем. 3) На основании сравнения II устанавливаются преимущества новой методики. Рассмотрим случайные величины:

– СВ X – К_у учебного материала отдельным студентом экспериментальной группы по ре-

зультатам контрольного тестирования.

– СВ У – К_у учебного материала отдельным студентом контрольной группы по результатам контрольного тестирования.

Вычислим наиболее важные числовые характеристики СВ Х и СВ Y – выборочные средние x_в и y_в (среднее арифметическое значение признака выборочной совокупности), выборочные дисперсии D_x и D_y (среднее арифметическое квадратов отклонений наблюдаемых значений признака от их средних значений x_в и y_в ) и выборочные средние квадратические отклоне-ния ст и ст (таб. 2) по формулам: xy

xв

k

Exf • n ii i=1

n

v        2

L⁽ x - x e г n

D = -------- в n

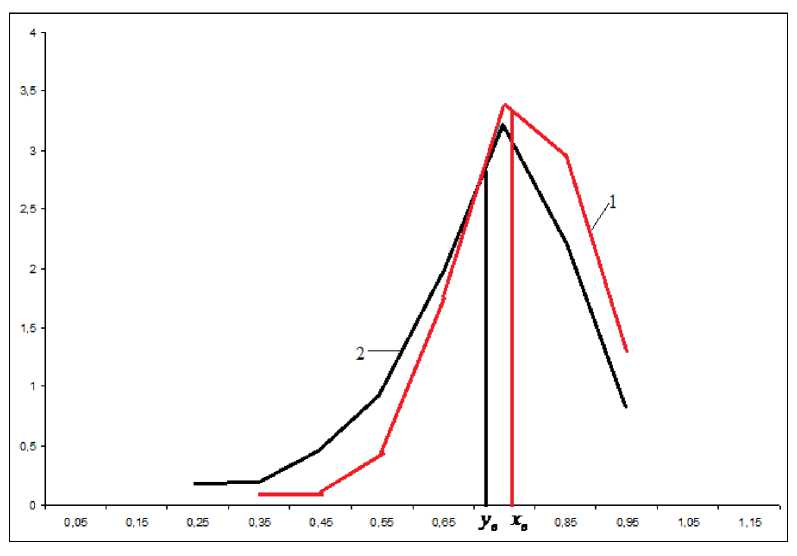
Рис. 2. Линии эмпирической плотности СВ Х и СВ У (1 – эмпирическая плотность распределения f * ( x ) , 2 - эмпирическая плотность распределения f * ( у ) )

Построим линии эмпирической плотности f *(x) и f *(у) (рис. 2). По виду этих линий выдвигаем статистические гипотезы о нормальных законах распределения СВХ и СВY с плотностью распределе- ния вероятности

- ( x - хв )^{2                                      - ( у} - У_а ⁾²

f ( х ) =---,= • e '   и f ( у ) = -Ц= • e ^о

о\П        о 2П

xy

Для проверки выдвинутой гипотезы используем один из критериев согласия – критерий согласия

Пирсона %2, состоящий в сравнении эмпирических и теоретических частот Теоретические частоты вычислим по известному алгоритму.

1. Нормируем СВ, т.е. переходим к величине Z =

X - ^Хв

^О в

, и вычисляем концы новых интервалов

z.=

xi

—

xв

О.,

; z _M =

x i + 1 - x e

о

в

где Ф ( Z ) =

1 г - x ² .     .                                                          _

;= e ² dx , Ф ( Z ) - функция Лапласа, находится по таблице ^п о

( Гмурман, В.Е. Теория вероятностей и математическая статистика / В.Е.Гмурман – М.: Высшая школа, 2003. – 462 – 463 с.; Вентцель, Е.С. Теория вероятностей и математическая статистика / Е.С.Вентцель – М.: Наука, Физматгиз, 1969. – 561 – 564 с.).

3. Находим искомые теоретические частоты n0. n0 = n • p0. Результаты наблюдений ni и вычис лений n0 после объединения интервалов с частотами n < 5 приведены в таб. 3 и 4.

Таб. 3. Эмпирические и теоретические           Таб. 4. Эмпирические и теоретические частоты СВХ                                 частоты СВY

Z	1	2	3	4	5
ni	7	19	37	32	14
n 0	8,327	23,413	36,439	28,275	12,546

i	1	2	3	4	5	6
ni	9	10	21	35	24	9
n	7,496	15,077	25,844	27,767	19,602	12,215

f n - n o ) 2

Вычислим наблюдаемые значения критерия х\б по формуле хнабл = —---о----, и сравним их с n критическими значениями х^р . Критические значения критерия хКР находим по таблице «Критические точки распределения х2» (Суходольский, Г.В. Основы математической статистики для психологов / Г.В. Суходольский - Л.: ЛГУ, 1972. - 428с.), задаваясь уровнем значимости а = 0,01. Уровень значимости -это вероятность ошибки 1-го рода, т.е. вероятность того, что верная гипотеза будет отвергнута. Число степеней свободы k вычислим по формуле k = S -1 - r, где r - число параметров предлагаемого распределения, для нормального закона их два: выборочная средняя xв и выборочное среднее квадратическое отклонение ст в (таб. 5).

Таб. 5. Наблюдаемые и критические значения критерия согласия х ² для случайных величин X и Y

Во всех случаях х^ <  х К _Р , следовательно, гипотезы о нормальном распределении случайных величин X и Y подтверждаются. Анализируя средние результаты тестирования в экспериментальной и контрольной группах (сравнение II на рис.1), видим, что средний результат в экспериментальной группе х_в = 0,763 лучше среднего результата в контрольной группе y_e = 0,720 на 5,97 %, при этом среднее квадратичное отклонение ст _х = 0,114 в экспериментальной группе меньше ст _у = 0,149 на 30,7 %, что говорит об эффективности применения предложенной методики. Кроме усредненных значений полезно бу-

дет сравнить рассеивание результатов тестирования относительно выборочной средней. Вычислим для этой цели коэффициент вариации V.

ст                                                               _

V = в • 100%, используемый для сравнения рас-хв сеивания вариационных рядов

V = (UH ^ 100% = 14,94% ,

*  0,763

0.149

V = ---100% = 20,69%, у 0,720

Случайная величина	Наблюдаемое значение критерия Пирсона х Н а6л	Критическое значение критерия Пирсона х К Р ( 5 ; а )
X	х Набл = 1,711	х Кр (2;0,01) = 9,2
Y	х Набл = 6,635	х Кр (3;0,01) = 11,3

Таким образом, в экспериментальной группе к концу обучения не только увеличился средний результат (на 5,97% по сравнению с контрольной группой), но и уменьшилось рассеивание резуль-

татов относительно среднего (с 20,69% до 14,94%), что, безусловно, подтверждает эффективность предложенной методики.

APPLICATION OF METHODS OF MATHEMATICAL STATISTICS FOR PROCESSING AND ANALYZING THE RESULTS OF A PEDAGOGICAL EXPERIMENT