Применение модели свободных электронов к тонким пленкам меди на поликоровых подложках

48 мм

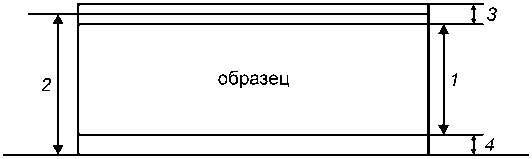
Рис. 1. Внешний вид полученных образцов. 1 – подложка, 2 – образец, 3 – зонды для измерения ЭДС Холла, 4 – зонды для измерения электропроводности

Применение модели свободных электронов представляет интерес для описания квазидву-мерного электронного газа в тонких металлических пленках. С практической точки зрения важно знать поведение электронов в тонкопленочных и гибридных схемах микроэлектроники, а также всевозможных твердотельных датчиках.

С уменьшением толщины пленки электронный газ приобретает свойство двумерного проводника, что в свою очередь сказывается на механизме рассеяния и зависимостях величин кинетических коэффициентов от толщины l - размерные эффекты. В настоящее время, теория размерных эффектов электропроводности тонких металлических пленок в целом разработана [1, 2]. Однако, ряд практически важных случаев применения тонкопленочных проводников, в частности в микроэлектронике, судя по доступной литературе, изучен не достаточно.

В данной работе приведены результаты экспериментальных исследований классического эффекта Холла от толщины пленок меди, сформированных на поликоровых подложках. Измерения проводились стандартным четырехзондовым методом в постоянном магнитном поле при постоянном токе. Измерительная установка и методика измерений описана нами ранее [3]. Погрешность измерений напряжений Холла при двух направлениях тока через образец составляет не более 10 %.

Образцы для исследования получены путем напыления меди через трафарет в вакуумной установке термического напыления УВН-5М. При этом сразу же формировались измерительные холловские зонды, а также токоподводящие зонды и зонды для измерения электропроводности. Примерная толщина пленки задавалась параметрами процесса напыления (температура испарителя, температура подложки, время открытия заслонки и т.д.) и контролировалась кварцевым измерителем толщины. Внешний вид полученных образцов с измерительными зондами и контактными площадками представлен на рис. 1.

Для надежности прижимных измерительных контактов, проводили дополнительное напыление меди на контактные площадки через специальный трафарет.

Примененный метод одновременного формирования образца и холловских зондов позволяет исключить проблему контактных шумов, что повышает разрешающую способность метода эффекта Холла. Неизбежно возникающие при этом на пряжения неэквипотенциальности вычитаются по известной методике [4] по результатам измерений при двух противоположных направлениях тока через образец.

Для исследований были изготовлены пять образцов пленок меди на поликоровых подложках, применяемых в радиоэлектронной промышленности для формирования гибридных, пленочных микросхем и микросборок. Подложки перед напылением подвергались плазмохимичиской чист- ке в серийной установке «Плазма 600». В таблице приведены значения напряжений Холла при комнатной температуре, полученные в этих образцах при индукции магнитного поля B и тока через образец I, а также значения толщины пленок dМСЭ рассчитанные по модели свободных электронов по известной формуле:

d МСЭ =

IB enUx

где U x – измеренное напряжение Холла, n – концентрация электронов проводимости в меди, рас-

N считанная из теории свободных и независимых электронов: n = —A р, где р - плотность меди. A

По нашим вычислениям n = 8,46 - 10 28 м^-3, в [5] приводится величина 8,47 - 10 28 м^-3.

Таблица

Сводная таблица экспериментальных данных

№ образца	1	2	3	4	5
U Холла , мВ	0,041	0,037	0,031	0,024	0,022
I , мА	100	100	100	100	100
B , Тл	1,14	1,14	1,14	1,14	1,14
d МСЭ , нм	147	161	195	250	274
d мик р , нм	120	150	180	220	250

0,045 0,04 0,035 0,03 0,025 X 0,02 ГО 0,015 0,01 0,005 0		1 2
	050        100       150       200       250       3 Толщина, нм	00

Рис. 2. Зависимость ЭДС Холла от толщины образцов

1 – график от измеренной толщины, 2 – график от рассчитанной толщины по МСЭ

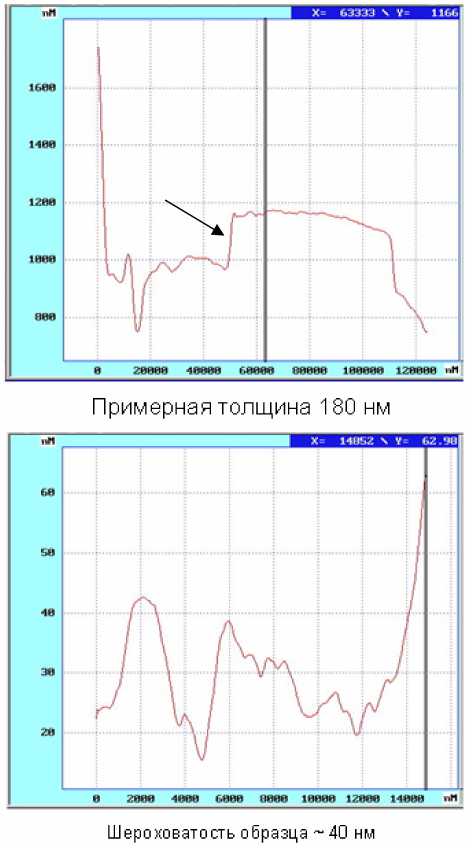
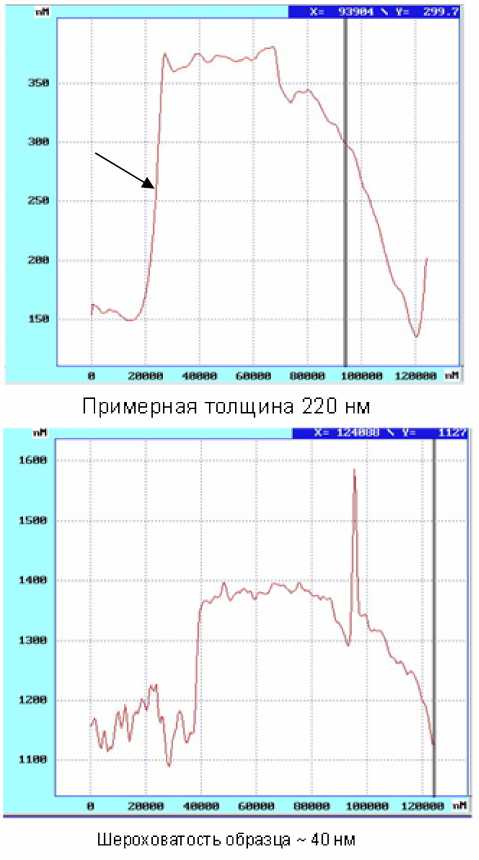
Толщину исследуемых пленок измеряли с помощью сканирующего зондового микроскопа Solver Pro P47. Для этого в трех местах образца делались тонкие сплошные (до подложки) царапины, вблизи которых сканировал зонд микроскопа, что позволило измерить толщину пленки и оценить шероховатость подложки. Усредненные значения толщины образцов, измеренные с помощью микроскопа d микр приведены в таблице. На рис. 3 и 4 приведены фрагменты результатов сканирования поверхности двух образцов. Стрелкой обозначен скачок, соответствующий толщине пленки. Сплошная вертикальная линия показывает линию среза для отображения дополнительных данных в интерфейсе микроскопа.

Результаты измерения средней толщины зондовым сканирующим микроскопом приведены в таблице ( d микр ).

На рис. 2 построена зависимость напряжения Холла от измеряемой толщины и от толщины рассчитанной по модели свободных и независимых электронов.

подложка

Рис. 5. 1 – Реальная толщина образца, 2 – толщина, рассчитанная по МСЭ, 3 – внешний оксидный слой, 4 – переходный слой

Рис. 3. Образец № 3                                     Рис. 4. Образец № 4

В целях согласования эксперимента и модели свободных электронов мы предлагаем рассматривать образец как слоистую модель, которая с одной стороны имеет границу раздела ме-талл-вакуум, а с другой стороны металл-диэлектрик.

На рис. 5 представлена эта модель.

Так как с обеих сторон образца имеются шероховатости, то в приграничной зоне электроны проводимости будут рассеиваться на дефектах, дислокациях. На границе раздела металл– диэлектрик будет возникать дополнительный потенциал. Все это будет обуславливать уменьшение ЭДС Холла, формируемой в переходном слое.

Для объяснения расхождения графиков зависимости в работе предложена качественная модель переходного слоя между подложкой и пленкой, распространяющейся в область металлической пленки. В области переходного слоя подвижность электронов существенно ниже по сравнению с объемом пленки, по этому вкладом переходного слоя в эффект Холла мож- но пренебречь. Если исключить из геометрической толщины пленки переходный слой, тогда графики на рис. 1 совпадут.

Также модель отвечает физической реальности электронного процесса и учитывает особенности кристаллизации пленок на поликоре при термовакуумном способе напыления.

Выводы и обсуждения

Расхождение толщин пленки измеренной прямым методом на сканирующем зондовом микроскопе и вычисленной по эффекту Холла на основе модели свободных электронов на наш взгляд можно устранить, если применить модель переходного слоя на границе подложка-пленка (рис. 3). Особенность этого слоя – наличие высокой концентрации дефектов на границе слоя со стороны подложки (шероховатость керамической поверхности, последствия термоударов при напылении) так и со стороны металла (эпитаксиальный эффект, дислокации несоответствия, упругие напряжения, сильно неравновесные условия кристаллизации на пористой подложке). Высокие концентрации структурных дефектов в переходном слое существенно уменьшают среднюю длину свободного пробега электронов по сравнению с основным объемом пленки. Если пренебречь вкладом в эффект Холла переходного слоя, то эффективную толщину рассчитанную по модели свободных электронов можно совместить с измеренной геометрической. При этом получается физически разумная толщина переходного слоя: близкая к длине свободного пробега в кристаллах меди (39 нм) и величине шероховатости подложки.