Применение мониторинга пассажиропотоков для организации оплаты проезда в поездах пригородного сообщения

Современная концепция ОАО «РЖД» уделяет большое внимание борьбе с безбилетным проездом в поездах пригородного сообщения [1]. В последнее время эта борьба усилилась. Но несмотря на применение различных средств (турникеты, ограждения) и связанные с ними дополнительные расходы регионального бюджета, так и не найдено эффективное решение этой проблемы.

В июле 2010 г. в период массовых перевозок, был осуществлён мониторинг по трем направлениям Челябинского участка железной дороги [3]. Анализировались количественные и качественные показатели пригородных перевозок, а также регулярность поездок пассажира; удовлетворенность расписанием движения электропоездов; возрастной контингент; место и удобство приобретения билета; был проведен учет пассажиров, садящихся в поезд без проездных документов.

Мониторинг пассажиропотока на Челябинском участке показал, что на всех остановочных пунктах пассажиры садятся в пригородный поезд без проездного документа. Право на льготный проезд (с учетом работников железнодорожного транспорта) имеется только у 10 % пассажиров.

Существующая система продажи билетов на вокзале и в поездах не дает возможности реального учета и контроля проезда пассажира. Пассажир может приобрести билет на одну зону, а ехать дальше. В пути следования пассажиры, садящиеся на остановочных платформах, где нет билетных касс, должны приобретать билеты у разъездного билетного кассира. В настоящее время разъездной билетный кассир – это работник аутсорсинговой компании. В пригородном поезде работает одна бригада разъездных билетных кассиров. Бригада состоит из двух человек, которые идут одновременно в одном вагоне (один по одной стороне, другой – по противоположной стороне). Это создает возможность для пассажиров, следующих в других вагонах этого пригородного поезда, проехать часть пути бесплатно.

Отношение менеджмента к пассажиру как потенциальному «зайцу» обречено на неуспех. Современный менеджмент качества предполагает научный подход, при котором организация, будучи зависимой от своих потребителей, должна понимать их текущие и будущие потребности, выполнять их требования и стремиться превзойти их ожидания [5]. Пассажиры являются потребителями услуги, предоставляемой железной дороги.

Первое впечатление о работе железнодорожного транспорта у пассажира создается при приобретении проездного документа (билета) на вокзале. Опрос показал, что пассажир затрачивает от трех до десяти минут на покупку билета в пригородной кассе. В среднем эта величина составляет 8,4 минуты, хотя в соответствии со стандартом время ожидания при покупке билета в пригородной кассе должно составлять не более семи минут. В соответствии с изложенным выше актуальной является проблема разработки и внедрения новых способов обеспечения оплаты проезда в пригородных поездах.

Одним из таких способов является сплошной мониторинг входного и выходного пассажиропотоков [2, 4] (т.е. «двойной учёт»). При входе в вагон пригородного поезда пассажиру выдаётся входная магнитная карточка с регистрацией станции входа с помощью терминала, а на выходе карточка возвращается контролёру с регистрацией станции выхода и проверкой оплаты стоимости проезда.

Автоматизированное обеспечение покупки билетов по системе «двойного учёта» позволяет удовлетворить потребности пассажиров в билетах, практически исключить потери за безбилетный проезд и негативные проявления человеческого фактора обслуживающего персонала, включая аутсорсинг. При осуществлении данного способа имеется возможность регистрации входного и выходного пассажиропотоков в общей базе данных с целью дальнейшей статистической обработки для объективного планирования как расписаний движения, так и работы кассиров [6].

В работе предложен способ статистической обработки результатов мониторинга, заключающийся в построении функции распределения вероятностей количества пассажиров для каждой возможной пары ( i , j > i ) станций отправления и назначения. Предложены способы планирования работы кассиров.

Математическая модель пассажиропотоков.

Общая схема пассажиропотоков на маршруте приведена на рис. 1.

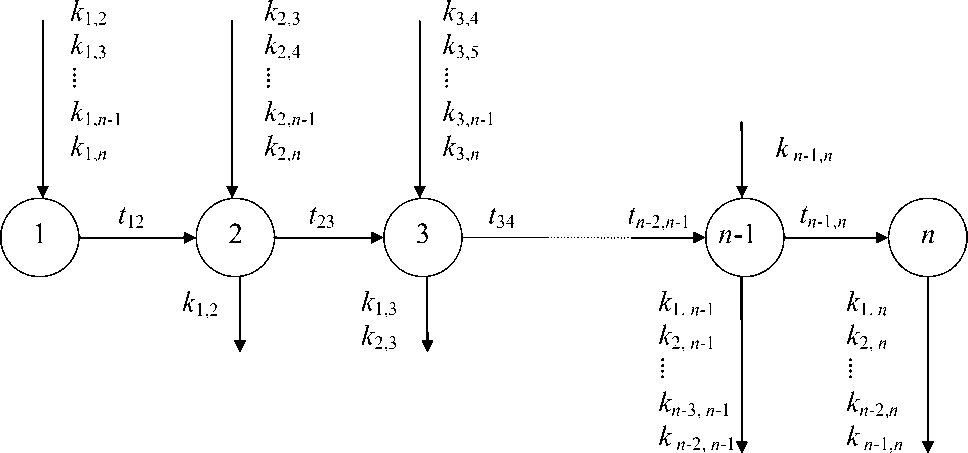
Рис. 1. Схема пассажиропотоков маршрута

Маршрут содержит станции 1,2,3…,n-1,n; время перегона между станциями i и i+1, i=1,2,3...,n-1, составляет величину t_{u +1}; коли-

n -1    n

p ^{( k} ) = ПП p i , j ■( k J ■) '

i =1 J = i +1

чество пассажиров, осуществляющих переезд от станции отправления i=1,2,3…,n-1 до станции назначения j=2,3_,n-1, равно Kz ..

В совокупности данные величины образуют           случайный           вектор k = { kji i = 1,2,3,..., n - 2, n -1, j = i +1,..., n -1, n}.

Полной характеристикой случайной величины является ее функция распределения. В рассматриваемом случае ведение общей базы данных всех прецедентов маршрута позволяет сформировать множество реализаций

K = {k(s) = {k

Время, требуемое на оплату проезда.

Время τ, требуемое на оплату одним

пассажиром своего проезда, также является случайной величиной. В классической теории массового обслуживания для времени обслуживания (аналога величины τ) принимается гипотеза об экспоненциальном распределении вероятностей. В настоящее время в связи с применением множества форм оплаты: предоплата, безналичная оплата, наличная оплата.

Далее будем предполагать, что длительность обслуживания кассиром пассажира

принимает следующие значения:

T = fl

^T о ,

^T 1 ,

^T 2 ,

^T 3 ,

предоплата или безналичная оплата, быстрая наличная оплата, медленная наличная оплата, отказ от оплаты.

Вероятность события {г r । / = 0123

pfl kiJ )=

s^

m

"!. J k J , 0. J k ’

далее будем обозначать через q . В соответствии с предельными теоремами теории вероятностей время t обслуживания k пассажиров будет

иметь асимптотически нормальное распределе-

Для маршрутов с фиксированным днем недели и временем отправления правдоподобной представляется следующая гипотеза.

Гипотеза независимости . Все случай-

ние вероятностей с математическим ожиданием

ные величины

k (s. : i = 1,2,3,..., n - 2, n - 1, J = i + 1,..., n - 1, n , s = 1,2,3,..., m

^T k = ^k - Z ³ = о ⁽ q - T )      ^и

⁽^ 2 = ^{k -} Z ³ = о ( q i -^{( T} k ^- t- ^{) 2} ) , функцию распределения

дисперсией т.е. иметь

являются независимыми.

Проведенное статистическое исследование пассажиропотоков на трех направлениях Челябинского участка железной дороги показало практическое отсутствие корреляции между исследуемыми величинами, что подтверждает целесообразность принятия данной гипотезы. Далее гипотеза независимости принимается.

В соответствии с теоремой Хинчина последовательности независимых случайных величин удовлетворяют закону больших чисел. Отсюда следует, что статистические функции распределения p(m) (k) случайных величин k с увеличением числа наблюдений m будут сходиться к фактическим функциям распределения p. .(k):  i = 1,2,3,...,n-2,n-1,  J = i +1,...,n-1,n.

Таким образом, в качестве математической модели пассажиропотока принимается функция распределения всей совокупности случайных величин k , которую в силу их незави- i , ^J

F k ( t ) = P T <  t } =Ф

- ^rk I , ^k J

где Ф ()   — функция стандартного

нормального распределения вероятностей.

симости можно представить в виде:

Применение результатов мониторинга пассажиропотоков.

Исследуемую систему можно отнести к системам массового обслуживания без отказов со штрафами за отклонение от директивного времени завершения обслуживания [7]. Если часть пассажиров к моменту завершения поездки окажется не обслуженными, то это приводит к штрафам за время задержки.

В ряде статей рассмотрены способы оценки систем с единственным [9] или несколькими [11] обслуживающими терминалами. Другие авторы [8, 10] изучают способы оптимального управления такими системами.

Отметим, что специфика рассматриваемой проблемы не позволяет использовать для ее анализа классические модели теории массового обслуживания.

Рассмотрим вопросы оценки качества обслуживания и планирования работы кассиров

в терминах функций распределения р. ^., полученных в результате мониторинга пассажиропотоков. Исследованы три формы обслуживания:

• 1.    Оплата при завершении поездки : на отрезке (j ' -1, j ) маршрута проезд оплачивают только выходящие на остановке j =2,3,., n пассажиры, перемещаясь после оплаты проезда в выходной накопитель.

• 2.    Оплата в начале поездки: все входящие пассажиры попадают во входной накопитель, а после оплаты проезда переходят в пассажирский салон.

• 3.    Оплата в течение поездки , когда пассажир может и должен быть обслужен на протяжении всей поездки.

Оплата при завершении поездки.

В соответствии с данной формой обслуживания на отрезке (j-1,j) маршрута проезд оплачивают только пассажиры, выходящие на остановке j. Число выходящих пассажиров будет равно k. = j k. . , а вероятность, с j    i=^i = 1  1 , j которой дискретная случайная величина kj принимает значение к, равна j-1              Л мк )= х In pJ Mb

{ k i,j > 0: i = ¹,²„. .J - ^1, X J = ^кi,J = ^k } ^k i^{J                 J}

жены, является в -квантилью  распределения

G j (T) , т.е.

T J ^{в )} = sup { t :   G j ( T ) < в } .

Поскольку функции G j ( T) ,   j =2,3,., n

( в )

являются монотонными, то все значения T

могут быть легко вычислены, например, методом половинного деления. Отсюда следует, что количество кассиров для обеспечения с вероятностью β кассового сбора со всех выходящих на перегоне (j ' -1 j ) пассажиров равно

N ^{( в )} =

T ^{( в} )

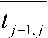
где I % I - наименьшее целое число, не

меньшее x .

Оплата в начале поездки.

В соответствии с данной формой обслуживания все входящие на станции i пассажиры попадают во входной накопитель, а после оплаты проезда переходят в пассажирский салон. Число входящих на станции i пассажиров

Еп k, а вероятность, с которой j=i i,

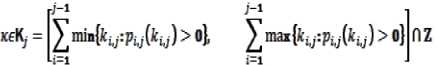
Функция p^ ( к ) полностью опреде-

дискретная случайная величина ki принимает значение k, равна

\(K •=       х      Ln/JM i          I                               n            Ik j =1+1             J

I ki , J > 0: J = i + 1, i + 2,... n ,   X к = к г

I                             J = i + 1 i ^, j    I

ляется функциями

p i,J ^(u) ,

т.е. результатами

K e ² K. = i

мониторинга, поэтому далее можно считать все

min K.  . : p.  .1 K.  . I > । n         I i, J    i, J k i, J J

^J = i ^{+ 1} X ⁿ       max] K. . : p. .

“ J = i ^{+ 1}      I i , J pi , J

n Z

значения

P.,( k )

заданными.

Для нахождения закона распределения вероятностей для значений времени T j , необходимого для сбора оплаты за проезд на перегоне (j ' -1 j ), воспользуемся формулой полной вероят-

Предположим, что к началу посадки на станции i во входном накопителе осталось необслуженными r_i пассажиров, и пусть q ( r ) - известная вероятность, с которой

ности:

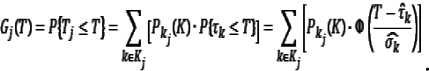
дискретная случайная величина r i принимает значение г. Тогда закон распределения для числа пассажиров s i = r i + k i , находящихся в накопителе после станции i, имеет вид

Отметим, что функции распределения G j ( T) , j =2,3,..., n строятся по результатам мониторинга и могут быть использованы для директивного планирования работы кассиров. Используя построенные функции G j ( T) , j =2,3,., n, можно определить количество кассиров, необходимое для обеспечения с вероятностью β кассового сбора со всех выходящих на станции j пассажиров.

Действительно, время T ^{( в )} , требуемое для того, чтобы на перегоне ( j ' -1 j ) с вероятностью в все выходящие пассажиры были обслу

Q Л s ) = ^p { s i = s } = X   p k i ^{( k} ) q Д ^r >^,

{ к , r : к + r = s }

Imm { ^ki + ri : pi ( ^кi ) • qi ( ri ) > 0

s ^e i = max { ^ki + ri ^: Pi ( ^ki )qi ( ri ) > ⁰

] n Z

.

Закон распределения вероятностей для значений времени T_i , необходимого для сбора оплаты за проезд на перегоне ( i , i +1), определим, воспользовавшись формулой полной вероятности:

h,(t) = p{t

=x

s e Si

Qs, ( s >ф t

Tjj k Qs  J

Время ( T^(в) ) , требуемое для того, чтобы на перегоне (i, i+1) с вероятностью в все находящиеся во входном накопителе пассажиры были обслужены, является в -квантилью распределения Hi (T, т.е.

T^(в) = sup{T:  Hi(T)< в} •

Доля обслуженных за время tii₊₁пассажиров равно

L. = min < 1, тi,^--- '          I , (T I- Ni где Ni - количество кассиров на пере гоне (i, i +1).

Таким образом, после перегона (i,i +1)

r+1 =(1^-Li)- si,

необслуженными останутся

причем закон распределения случайной величи- ны r имеет вид q ,+,(r) = Qsi (Lr •(1 - Li) J).

Итак, зная закон распределения количества пассажиров ri , оставшихся в накопителе к концу перегона (i-1, i), легко получить закон распределения количества пассажиров ri+1, оставшихся в накопителе к концу перегона (i,i +1). Поскольку r 1 с вероятностью единица принимает нулевое значение, то при заданных значениях Ni, i =1,2,..., n -1 могут быть определены законы распределения всех случайных величин ri , i =1,2,.,n-1. Значения Ni могут быть определены из решения задачи оптимизации n-1                                                                                        'I

XNi:(Vz = 1,2,...,n-1)(P{si>s_}< a) [, i=1

min

Ni: i=1,2,..., n-1

где      - вместимость накопителя для max входящих пассажиров, a - уровень доверия.

Оплата в течение поездки.

В соответствии с данной дисциплиной обслуживания пассажир может и должен быть обслужен на протяжении всей своей поездки. Данное требование может быть формализовано следующим образом.

Количество пассажиров, которое необходимо обслужить на промежутке от станции l=1,2,.,n-1 до станции m=l+1,l+2,.,n, равно L = V         k . Вероятность, с кото- lm     (—j( i, j ): l < i < J' < n i,J рой случайная величина Llm примет значение L, равна

PL,^(L)PLlm = ^L}=₍                     ^X

| Ki, j > ^l< i <j< n, Zy :i<,<j< nk.j-L '

П    p IT

(i, j I: l< i < J< n i, J Ik    I

V                               I i,^J)J

Для нахождения закона распределения вероятностей для значений времени Tlm, необхо- димого для обслуживания пассажиров на промежутке от станции l=1,2,.,n-1 до станции m=l+1,l+2,.,n, воспользуемся формулой полной вероятности:

Gm(T) = P{Tm < T}= XpLm (L)• P{tl< T}] = L:Pm (L)>0

= X P  (L

^L:PLm^(L )>⁰L             V  ^aL   v

Время Tв, необходимое для обслужи- вания пассажиров на промежутке от станции l=1,2,.,n-1 до станции m=l+1,l+2,.,n, является в -квантилью распределения Glm ( T), т.е.

Tm^в)= sup {T : Glm (T)< в} .

Резерв времени на обслуживание пассажиров на промежутке от станции l=1,2,.,n-1 до     станции     m=l+1,l+2,.,n     равен

—       m -1        ______________ ____________

T = > t , следовательно, количество lm    i=^i=l i, i+1

кассиров на данном промежутке должно быть не меньше

Nm =

^ ^{( в} ) lm

Пусть (lо, mo ) = arg ^maX(l,m) ^Nlm , тогда очевидно, что минимальное количество кассиров Ni на всех перегонах (i, i + 1) : l_Q< i< m₀ равно Nlm . Минимальное количество кассиров на оставшихся перегонах определяется путем исключения фрагмента (1₀, m о) из маршрута и рекурсивным применением данной процедуры для образовавшихся фрагментов.

Заключение

Автоматизированное обеспечение покупки билетов по системе «двойного учёта» позволяет не только удовлетворить потребности пассажиров в билетах, но и практически исключить потери за безбилетный проезд, негативные проявления человеческого фактора обслуживающего персонала, включая аутсорсинг. При осуществлении данного способа имеется возможность регистрации входного и выходного пассажиропотоков в общей базе данных с целью дальнейшей статистической обработки для объективного планирования как расписаний движения, так и работы кассиров.

Предложенные в работе методики обработки результатов мониторинга с целью директивного планирования работы кассиров демонстрируют эти возможности. Дальнейшее обобщение результатов данной работы на проблемы оперативного управления, основанного на вычислении апостериорных распределений веро- ятности, является предметом будущих исследований.