Применение нечеткой и четкой математических моделей в гибридном управлении процессом одностадийного измельчения замороженного мясного сырья

В соответствии с Указом Президента Российской Федерации1 переход к передовым интеллектуальным производственным технологиям, а также создание безопасных и качественных продуктов питания относятся к приоритетам научно-технического развития страны. Интеллектуальная система управления (далее – ИСУ) процессом одностадийного измельчения замороженного мясного сырья на основе прогностической адаптивной модели рассчитывает прогноз температуры пограничного слоя мяса в зоне контакта сырья с режущим инструментом измельчителя. По результатам расчета ИСУ устанавливает режимные параметры процесса измельчения: скорость резания мяса и скорость подачи сырья в зону измельчения с целью стабилизации размера получаемой мясной стружки. На основе математической модели процесса измельчения методом фрезерования (одностадийного измельчения) ИСУ рассчитывает математическое ожидание и дисперсию размера мясной стружки как случайной величины. Основываясь на данных, полученных от измерительных датчиков, комплектующих систему, а также на данных аналитического расчета, ИСУ может вычислить границы «коридора» и степень «размытости» границ, в которых будет находиться размер мясной стружки. Отметим, что ИСУ накапливает статистическую информацию о процессе измельчения, обучаясь в процессе работы. Это является характерной чертой современных интеллектуальных систем управления2 [1; 2].

Для полной автоматизации технологической обработки измельченного мяса и производства высококачественной готовой продукции актуальной задачей является стабилизирование средствами ИСУ режимных параметров процесса резания замороженного сырья, установленных с использованием нечеткой модели управления. Для решения указанной задачи целесообразно использовать математическую модель одностадийного измельчения сырья по методу фрезерования, применяемую в области четкой (булевой) логики [3].

Целью данного исследования являлась разработка алгоритма гибридного управления одностадийным измельчением замороженного мясного сырья с использованием нечеткой и четкой математических моделей управления. Задачей исследования являлась разработка адаптивной прогностической модели определения температуры пограничного слоя блочного мяса в процессе его переработки и математической модели на основе теории нечетких множеств для расчета режимных параметров измельчения сырья с использованием данных прогноза.

Обзор литературы

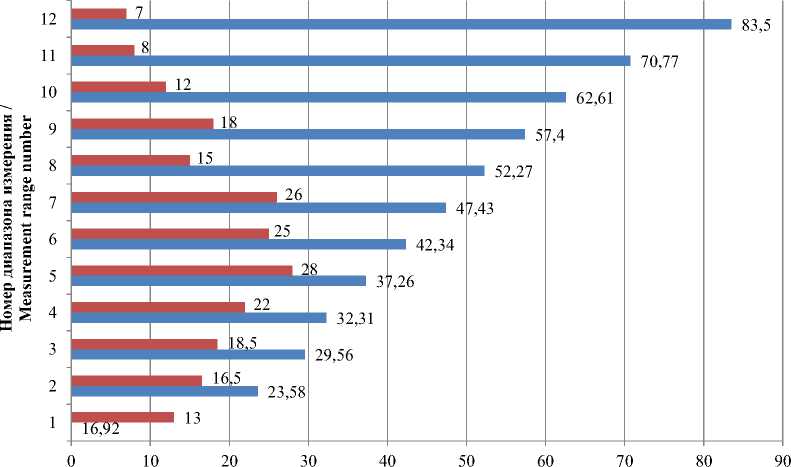
Температурный контроль замороженного мяса в процессе его измельчения по методу фрезерования является особо важной задачей. Температура сырья в зоне резания повышается из-за интенсивного теплообмена между тонким пограничным слоем мяса, срезаемым рабочим инструментом измельчителя, и самим этим инструментом, разогретым в процессе работы. Исследование микроструктуры тонко измельченного сырья показало, что толщина получаемой мясной стружки в зоне контакта с режущим инструментом составляет доли миллиметра [4]. Гистограмма распределения толщины мясной стружки при комплектации одностадийного измельчителя фрезой цилиндрической насадной по ГОСТ 29092-91 представлена на рисунке 1. Режимные параметры процесса измельчения составили: скорость подачи сырья на фрезу – 0,0243 м/с; частота вращения фрезы – 2289,14 мин-1.

Толщина мясной стружки, мкм / Thickness of meat pieces, µm

Число измерений в каждом диапазоне / Number of measurements in each range

Cредние значения толщины мясной стружки / Average values of the thickness of meat pieces

Р и с. 1. Гистограмма распределения размера (толщины) мясной стружки при одностадийном измельчении. Диапазоны измерения: 1 - 14-20 мкм; 2 - 20-26 мкм;

3 – 26–30 мкм; 4 – 30–35 мкм; 5 – 35–40 мкм; 6 – 40–45 мкм; 7 – 45–50 мкм; 8 – 50–55 мкм; 9 – 55–60 мкм; 10 – 60–66 мкм; 11 – 66–76 мкм; 12 – 76–91 мкм

F i g. 1. Histogram of the distribution of the thickness of meat chips during single-stage mincing. Measuring ranges: 1 - 14-20 pm; 2 - 20-26 pm; 3 - 26-30 pm; 4 - 30-35 pm; 5 - 35-40 pm;

• 6 - 40-45 pm; 7 - 45-50 pm; 8 - 50-55 pm; 9 - 55-60 pm; 10 - 60-66 pm; 11 - 66-76 pm;

12 – 76–91 µm

Нагрев замороженного мяса до температуры, близкой к его криоскопической температуре, обуславливает проявление пластических свойств мяса. На рисунке 2 представлено проявление пластических свойств сырья в процессе его одностадийного измельчения многолезвийным инструментом [5]. Как видно из рисунка 2, в процессе измельчения сырья из-за его пластичности возрастает толщина срезаемой мясной стружки, что приводит к увеличению дисперсии указанного размера получаемой стружки относительно среднего его значения (математического ожидания) и отрицательно сказывается на гомогенности получаемого измельченного продукта. Для снижения дисперсии размера стружки следует увеличить скорость резания сырья, сведя к минимуму эффект его продавливания в канавку между смежными зубьями фрезы. Поддерживать максимально высокой частоту вращения фрезы в течение всего временного периода измельчения партии блочного мяса, перерабатываемого на технологической линии непрерывного действия, нецелесообразно для снижения энергозатрат на процесс резания сырья.

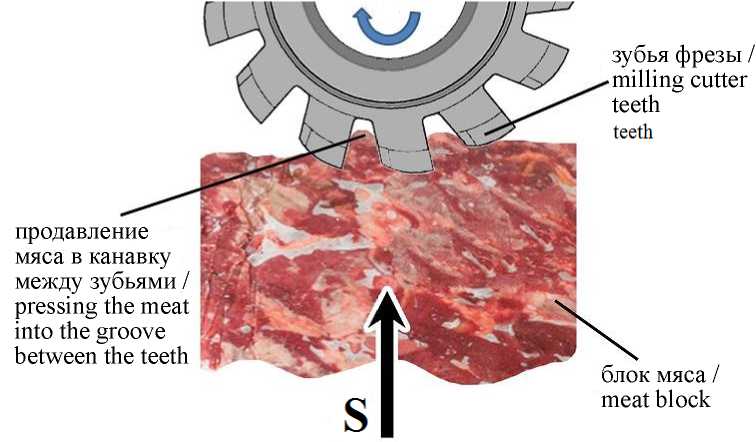
Р и с. 2. Проявление пластических свойств мяса, S – направление подачи сырья

F i g. 2. Manifestation of meat plastic properties, S – feed direction of the meat

К особенностям фрезерования блочного мяса следует отнести жесткое крепление блока сырья в направляющих плоскостях рабочей камеры измельчителя, что приводит к пластическим деформациям поверхностного слоя мяса. Известно, что пластические деформации материала приводят к его нагреву3. Кроме того, при подаче сырья на режущий вал измельчителя работа сил трения блока мяса о направляющие плоскости переходит в тепловую энергию, нагревающую его поверхностный слой.

К причинам изменения температуры пограничного слоя блочного мяса в процессе его переработки можно отнести: нагрев рабочего инструмента измельчителя при длительной работе технологической линии; возможные перерывы в работе линии и «отепление» сырья, находящегося вне морозильной камеры; использование блоков мяса при различной температуре их хранения перед измельчением и т. п. Отсюда возникает задача регулирования режимных параметров процесса резания сырья в зависимости от его температуры. Следовательно, необходимо осуществить измерение температуры мяса при его измельчении в режиме реального времени работы одностадийного измельчителя. Для решения сформулированной выше задачи регулирования следует знать температуру пограничного слоя мяса непосредственно в зоне резания сырья. Однако, учитывая инерционность электромеханической системы измельчителя, влияющую на время переключения режима резания, определять искомую температуру целесообразно со временем упреждения, основываясь на данных измерения температуры и расчетных данных,

• Vol. 33, no. 4. 2023 ENGINEERING TECHNOLOGIES AND SYSTEMS ^Т^ полученных для пограничных слоев мяса, отделенных от массива этого же мясного блока в предыдущие моменты времени послойного измельчения сырья. Другими словами, речь идет о расчете прогноза температуры пограничного слоя мяса на несколько временных интервалов вперед, проведенном компьютером, комплектующим систему управления, в режиме реального времени без участия оператора. Минимальное суммарное значение указанных временных интервалов, глубина прогноза, обуславливается инерционностью системы управления и определяется расчетным путем.

Авторы предлагают использовать математическую модель, разработанную на основе теории нечетких множеств [6], для расчета режимных параметров измельчения сырья с использованием данных прогноза температуры пограничного слоя блочного мяса в процессе его переработки. Указанная модель обуславливает зависимость параметров режима измельчения сырья от его температуры c учетом изменения структурно-механических свойств замороженного мяса, влияющих на его измельчение, в температурных диапазонах, имеющих нечетко определенные границы. Отметим, что нечеткие математические модели могут быть эффективно использованы в управлении биотехнологическими и пищевыми процессами, которые во многих случаях имеют нечеткие границы диапазонов изменения параметров, характеризующих эти процессы [7; 8; 9]. Например, теорию нечетких множеств целесообразно применить для решения задач сенсорной оценки при вычислении данных в неопределенных и неточных условиях, что может привести к «более точной физической интерпретации» [10].

Материалы и методы

Объектом исследования являлся процесс одностадийного измельчения замороженного блочного мяса (говядины второго сорта, далее по тексту – говядина), который осуществляли на лабораторной установке одностадийного измельчения производительностью 400 кг/ч. Длина экспериментальных блоков замороженного мяса, измельченных в лабораторных условиях и нарезанных из блоков промышленного размера, составила 0,3 – 0,4 м.

Полученные ранее экспериментальные данные [4] подтверждают гипотезу о нормальном законе распределения нагрузки на фрезу при измельчении блоков промышленных размеров. Случайный процесс нагрузки на фрезу предполагаем стационарным процессом, обладающим свойством эргодичности4. Указанные приближения дают основание использовать экстраполяцию для прогнозирования температуры слоев мяса, отделяемых от массива мясного блока в процессе его измельчения.

Принимается допущение, принятое в практике холодильной технологии, о параболическом распределения температуры по сечению тела простой формы. В рассматриваемом случае – параллелепипеда5. Сечение блока мяса приближенно рассматривается как плоскопараллельная фигура без учета кривизны поверхности резания.

Выбор метода прогнозирования средней температуры сечения блока замороженного мяса в процессе его измельчения проводили в соответствии с современными представлениями об адаптивных методах краткосрочного прогнозирования временных рядов [11; 12].

Регистрацию электромагнитного момента приводного электродвигателя механизма резания одностадийного измельчителя в рабочем режиме производили с помощью цифрового многоканального самописца Flash-Recorder-2-16RTC-SD.

Для разработки нечеткой математической модели управления использовали широко распространенный в промышленных приложениях алгоритм нечеткого вывода Э. Мамдани [13].

Математическое моделирование температурного контроля замороженного мясного сырья с использованием нечеткой модели осуществляли в вычислительной среде MATLAB (пакет Fuzzy Logic Toolbox)6.

Результаты исследования

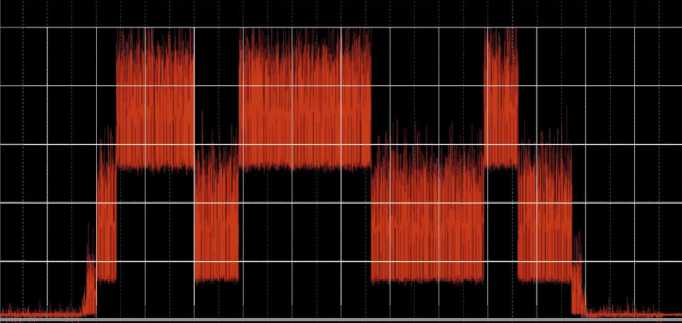
В результате экспериментального изучения процесса одностадийного измельчения замороженного мяса установлено, что электромагнитный момент электродвигателя привода механизма резания измельчителя изменяется в рабочем режиме. Это можно подтвердить данными измерения электромагнитного момента приводного электродвигателя, приведенными на рисунке 3. Изменение электромагнитного момента (момента на валу) приводного электродвигателя механизма резания одностадийного измельчителя в рабочем режиме объясняется текстурной и структурной неоднородностью перерабатываемого мясного сырья. На рисунке 3 можно видеть этапы измельчения блочного мяса: от нулевого момента времени до 3,5 с ‒ подача блока мяса на режущий вал (холостой ход измельчителя); с 3,5 с до 24 с - процесс измельчения сырья; с 24 с до 28 с - отвод подающего штока измельчителя в начальное положение (второй холостой ход).

M,Nm<

10"

0         2        4        6        8        10       12       14       16 1S 20       22       24       26       28

Р и с. 3. Данные измерения электромагнитного момента приводного электродвигателя механизма резания одностадийного измельчителя в рабочем режиме

t, S

F i g. 3. Measurement data of the electromagnetic torque of the drive motor of the single-stage mincing mechanism in operating mode

Отметим также, что для промышленного образца одностадийного измельчителя предполагается использовать наборный режущий вал, составленный из стандартных фрез. Длина режущей части вала должна соответствовать максимальному линейному размеру блоков замороженного мяса по ГОСТ Р 54704-2011. В этом случае расчетная производительность процесса измельчения составляет 5300 кг/ч.

Учитывая данные экспериментального исследования, следует стабилизировать средствами ИСУ режимные параметры процесса резания мяса в целях получения гомогенного по размеру мясной стружки измельченного сырья.

Температурный режим поверхностного слоя мяса, прилегающего к зоне контакта с многолезвийным инструментом в рабочей камере измельчителя, может значительно отличаться от условий, определяющих температурный режим такого же слоя в блоке, находящемся вне измельчителя, например в напольной тележке. В нашей работе во время опытных измельчений на экспериментальной установке наблюдалось частичное размораживание поверхностных слоев мяса с выделением влаги. Отсюда следует задача определения температуры слоя мяса непосредственно в зоне измельчения для корректного учета изменений его пластических свойств при нагреве.

Для решения указанной задачи необходимо экспериментально измерить температуру в зоне контакта лезвия рабочего инструмента измельчителя с сырьем в начальный момент времени отделения мясной стружки от массива блока. Технически это возможно сделать бесконтактным способом в точке вхождения зуба инструмента в массив мясного блока. Далее расчетным способом определяется усредненная температура по дуге резания при допущении, что в центре блока первоначальная температура неизменна и равна температуре хранения сырья в морозильной камере перед измельчением.

Метод бесконтактного измерения температуры в обрабатывающей промышленности представляет собой регистрацию теплового излучения отдельных участков детали или инструмента в процессе обработки. Предложенную схему измерения7 по указанному методу можно адаптировать для температурного контроля блочного мяса в рассматриваемом случае (рис. 4). При измельчении блока замороженного мяса 1 фрезерным валом измельчителя 2 тепловое излучение площадки контакта сырья с многолезвийным инструментом 3 аккумулируется в объективе 5 и передается в фоточувствительный элемент 6. Сигнал усиливается в электронном усилителе (на рисунке 4 не показан) измерительного устройства 4 и передается в конечном итоге в управляющую вычислительную машину (УВМ). Сигнал в ИК-диапазоне может приниматься с контактной площадки размером 0,04×0,07 мм при точности измерения ±2 – 3%. Таким образом, схема измерения температуры пограничного слоя мяса может быть использована для реализации прогноза температуры сырья в зоне резания.

На основе рассмотренной схемы следует создать устройство измерения с применением современной инструментальной базы для решения задачи температурного контроля сырья.

Очевидно, что температура на поверхности слоя мяса, измеренная экспериментальным способом, отличается от температуры в центре этого же слоя мяса, то есть в центре мясного блока. В практике холодильной технологии существуют приближения среднеобъемной температуры тел простой формы при допущении параболического распределения температур по сечению тела8. В рассматриваемом случае под сечением тела следует понимать поверхность резания мясного блока в текущий момент времени, которую представим как плоскопараллельную фигуру в виде сечения параллелепипеда – формы мясного блока.

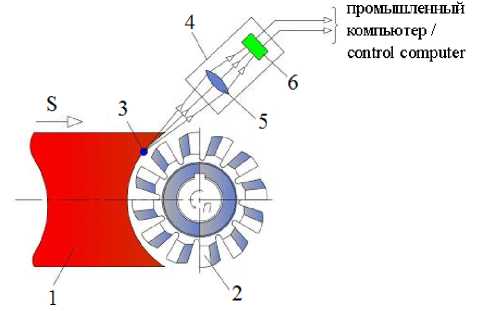
Р и с. 4. Схема измерения температуры пограничного слоя: 1 – блок замороженного мяса;

2 - фрезерный вал измельчителя; 3 - участок поверхности резания мясного блока;

4 - измерительное устройство; 5 - объектив; 6 - датчик ИК-излучения;

S - направление подачи блока сырья на фрезерный вал измельчителя;

n – частота вращения фрезерного вала измельчителя

F i g. 4. Scheme of temperature measurement of boundary layer: 1 - block of frozen meat;

• 2 - milling shaft of the mincer; 3 - area of the mincing surface of the meat block;

• 4 - measuring device; 5 - lens; 6 - IR-sensor; S - direction of feeding the meat block to the milling shaft of the mincer; n – rotation frequency of the milling shaft of the mincer

Поместим начало системы координат в центр мясного блока, температуру в центре блока обозначим Т_c . Ось « х » будет направлена по нормали к поверхности блока, температуру которой обозначим Т_s . Расстояние от центра блока мяса до его поверхности обозначим 0,5 Н , где Н - высота блока промышленного типоразмера, равная высоте бруса. Отметим, что высота блока Н соответствует ширине фрезерования при горизонтальном расположении режущего вала. В соответствии с принятым допущением о параболическом распределении температур по сечению блока температуру точки на поверхности резания с координатой « х » можно представить как:

T = T - ( T - T )------- ,                        (1)

x s Vx c’ (0,5 H )2

где Т_х – температура в точке « х ».

Решая уравнение (1) для множества точек в интервале xc < x < xs, где xc = 0, xs = 0,5 Н, получают массив значений температуры сечения блока мяса по дуге резания от поверхности до центра блока. Усредняя полученные значения, определяют среднюю температуру мяса поверхности резания перерабатываемого блока в текущий момент времени. Обозначим эту среднюю температуру как Tt, где t -текущий момент времени.

Ряд значений средней температуры поверхности резания для следующих друг за другом сечений мясного блока, последовательно срезаемых рабочим инструментом измельчителя в процессе измельчения сырья, представим в виде временного (динамического) ряда T . Каждый член (уровень) такого ряда связан с соответствующим моментом времени или временным интервалом. Уровни временного ряда Т формируются под воздействием различных факторов. Некоторые из них, например структурная и текстурная неоднородность блочного мяса, имеют случайный характер.

Задачи исследования временных рядов группируют следующим образом:

• 1.    Описание изменения анализируемого показателя (расчет среднего темпа роста; применение сглаживающих фильтров, уменьшающих колебания уровней ряда во времени; подбор кривых, характеризующих тенденцию развития и др.).

• 2.    Объяснение механизма изменения анализируемого показателя (регрессионный анализ).

• 3.    Статистическое прогнозирование (экстраполяция обнаруженных тенденций развития).

Для реализации температурного контроля сырья, перерабатываемого на технологической линии, необходимо решить задачу из третьей группы.

Под экстраполяцией в прогнозировании понимают продление в будущее тенденции, наблюдавшейся в прошлом [15]. В рассматриваемом случае необходимо оценить температуру Т в процессе переработки блока мяса на несколько шагов вперед по временной шкале. Тогда задачу исследования временного ряда Т можно сформулировать так: основываясь на данных измерения температуры поверхности блока сырья T s при послойном его срабатывании на определенном временном промежутке, оценить на несколько шагов (несколько слоев мяса, последовательно отделяемых от массива блока) вперед во времени температуру Т методом прогнозирования (экстраполяцией).

Как указывается в литературе [11; 12], экстраполяция базируется на следующих допущениях: во-первых, процесс изменения исследуемого параметра во времени можно охарактеризовать трендом, то есть плавной траекторией; во-вторых, принимается гипотеза об инерционности протекания исследуемого процесса (условия, определяющие тенденцию развития в прошлом, останутся без существенных изменений в будущем). В рассматриваемом случае эти требования к объекту исследования выполняются, поскольку, во-первых, переработка сырья на технологической линии проходит при неизменной температуре окружающей среды, оговоренной в Техническом регламенте Таможенного союза 034/2013 «О безопасности мяса и мясной продукции»; во-вторых, процесс измельчения сырья характеризуется стабилизацией параметров режима его резания в целях получения гомогенного по размеру мясной стружки измельченного продукта.

Экстраполяция временного ряда дает возможность получить как точечную прогностическую оценку, так и интервальную оценку (расчет доверительных интервалов прогноза) [16]. Точечная оценка для температурного контроля сырья не имеет практического интереса, так как температурное поле мясного блока является непрерывным. Кроме того, изменение структурно-механических свойств замороженного мяса, влияющих на его измельчение, характеризуется не пороговым (точечным) значением температуры мяса, а диапазоном значений температуры. Таким образом, для температурного контроля мяса следует выбрать расчет интервальной прогностической оценки.

Для краткосрочного прогнозирования временного ряда Т выберем экстраполяцию по экспоненциальной средней. Под краткосрочным прогнозированием понимают расчет прогностической оценки на основе изолированного ряда динамики процесса без выделения и анализа тренда. Краткосрочность прогноза температурного контроля сырья обуславливается необходимостью оперативно оценить среднюю температуру ряда слоев мяса, которые предстоит отделить от массива мясного блока в процессе его измельчения. Следовательно, необходимо вычислить прогноз изменения указанной температуры на ограниченном количестве данных измерения температуры Т_s , полученных в процессе измельчения сырья.

Экспоненциальная средняя временного ряда Т_{t m} (сглаженное значение уровня ряда) определяется как:

T m = Z ; “ ( 1 - “ )Ч r ,                       (2)

где T_m - экспоненциальная средняя ряда Т на момент времени t ; а - коэффициент, характеризующий вес текущего наблюдения (параметр сглаживания), 0 < α < 1, T_t–r уровень ряда Т , находящийся на расстоянии r от момента времени t .

Сумму (2) можно записать как:

T = Г    + a Гг, - Г     ,                      (3)

tm       (t-1) m           t      (t-1) m где Тt ‒ фактический уровень ряда в момент времени t.

Если Т ■ t _{-r) m} считать прогнозом уровня ряда, то разность ( Т - Т , t -1) _m ) определяет погрешность этого прогноза. Тогда для краткосрочного прогнозирования оценка Т_tm учитывает наблюдавшуюся в момент времени t ошибку прогноза. Таким образом, экспоненциальная средняя ряда адаптируется к новым условиям течения процесса изменения контролируемого параметра во времени. Под адаптивным прогнозированием понимается разработка прогноза с самообучением. Вычисляемые средние уровней ряда с каждым шагом во времени изменяются с учетом ошибки прогноза на предыдущем шаге. Отметим, что для ИСУ технологической линией производства мясных продуктов с применением одностадийного измельчения сырья характерна обучаемость системы в процессе функционирования [3].

Для разработки адаптивных прогностических моделей рассчитывают экспоненциальные средние более высоких порядков путем многократного экспоненциального сглаживания:

T m ⁽ '^ « T m ⁽ ' ^Ч "  « ) T - 1 ) m ⁽ ^ ’ ’                     (4)

где к - порядок средней.

Как видно из формулы 4, в вычислении экспоненциальной средней на k этапе расчета используется полученное ранее значение экспоненциальной средней на ( к - 1) этапе расчета. Такой последовательностью вычислений достигается многократное экспоненциальное сглаживание.

От точечных прогностических оценок (4) следует перейти к интервальной оценке:

T m + t ^_X 1 +      ’

2 - а

Пищевые системы где σ ‒ среднее квадратическое отклонение от Тtm; ta – значение t-статистики Стьюдента.

Адаптивную модель прогнозирования на N шагов (во времени) вперед с использованием экспоненциальных средних первого и более высоких порядков можно записать в виде полинома степени k :

T+N) m = at + bN + cN2 + - + mN, (6)

где a t , b_t ,... m t - параметры прогнозирования, которые могут быть получены как линейные комбинации экспоненциальных средних соответствующих порядков.

Дисперсия прогноза (6) для записи доверительного интервала прогнозирования определяется по приближенным формулам, приведенным в литературе9.

Следует отметить, что продолжительность периода упреждения ( N ) должна превышать постоянную времени, определяемую инерционностью (механической и электромагнитной) объекта управления, то есть видами оборудования, комплектующими технологическую линию производства мясных продуктов и реализующими процесс измельчения сырья. Это необходимо для своевременного переключения режима резания сырья в соответствии с изменением температуры перерабатываемого мяса.

Этапы осуществления температурного контроля сырья можно представить алгоритмом функционирования и графически отобразить его в виде блок-схемы (рис. 5). После проведения измерений температуры мяса и аналитических расчетов с использованием результатов измерений управляющий компьютер без участия оператора принимает решение о необходимости изменения режима резания сырья с целью поддержания заданной степени его измельчения. Это решение принимается на основе экспертной базы знаний, хранящейся в памяти управляющего компьютера.

Известно, что изменения физико-механических свойств мяса при его измельчении в замороженном виде оказывают существенное влияние на режущую способность измельчителей, а также энергозатраты на осуществление процесса¹⁰, а температура замораживания сырья влияет на изменения коэффициента Пуассона ( и ) 11 .

Из результатов приведенных исследований видно, что структурно-механические свойства замороженного мяса, влияющие на процесс его измельчения, характеризуются температурными диапазонами, в которых их значения существенно изменяются. Таким образом, для температурного контроля сырья в процессе его измельчения следует рассматривать диапазоны изменения температуры замороженного мяса, причем для различных структурно-механических свойств границы этих диапазонов на температурной шкале могут быть совмещены. В этих условиях возникает неопределенность в установлении режимных параметров резания сырья в целях поддержания заданной степени его измельчения. Это обуславливает целесообразность применения нечеткой модели управления для реализации температурного контроля сырья в рассматриваемом случае.

• ⁹    Лукашин Ю. П. Адаптивные методы краткосрочного прогнозирования временных рядов. М. : Финансы и статистика, 2003. 416 с.

• ¹⁰    Илюхин В. В. Физико-технические основы криоразделения пищевых продуктов. М. : Агро-промиздат, 1990. 207 с.

• ¹¹    Чижикова Т. В. Машины для измельчения мяса и мясных продуктов. М. : Легкая и пищевая промышленность, 1982. 302 с.

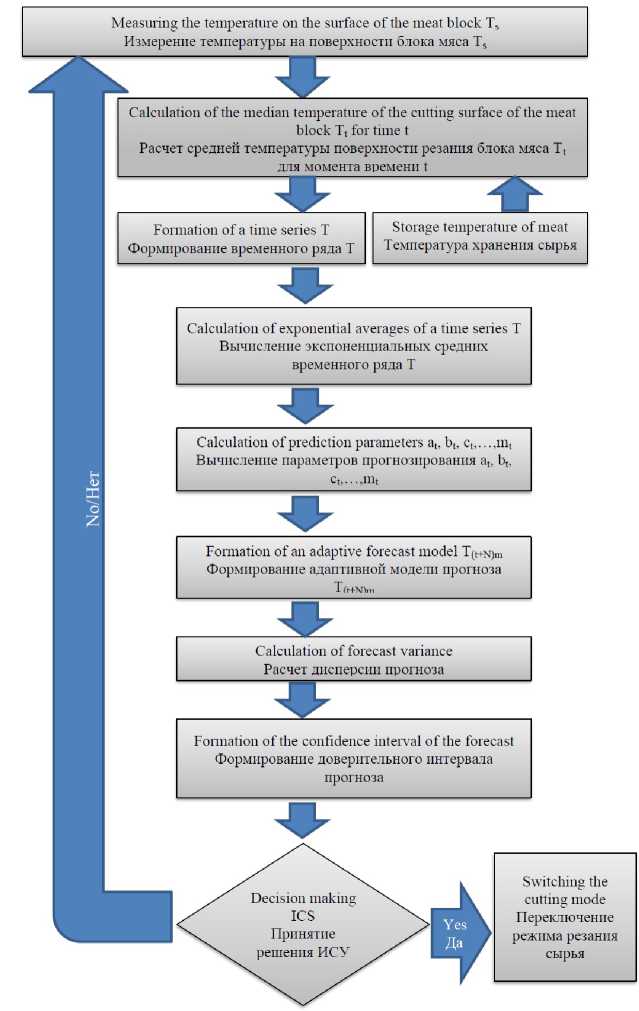
Decision making ICS Принятие решения ИСУ

Formation of a time series T Формирование временного ряда T

Storage temperature of meat Температура хранения сырья

Calculation of the median temperature of the cutting surface of the meat block Tt for time t

Расчет средней температуры поверхности резания блока мяса Tt для момента времени t

Measuring the temperature on the surface of the meat block Ts Измерение температуры на поверхности блока мяса Ts

Formation of the confidence interval of the forecast Формирование доверительного интервала прогноза

Calculation of exponential averages of a time series T Вычисление экспоненциальных средних временного ряда Т

Calculation of prediction parameters at, bt, Ct,...,mt Вычисление параметров прогнозирования at, bt, ct,...,mt

Fonnation of an adaptive forecast model T(t+N)m Формирование адаптивной модели прогноза Tft+№m

Switching the cutting mode Переключение режима резания сырья

Calculation of forecast variance Расчет дисперсии прогноза

Р и с. 5. Блок-схема температурного контроля F i g. 5. Flowchart of temperature control

Правила нечеткого управления дают возможность использовать для контроля технологического оборудования полную информацию о его функционировании при различных режимах управления в зависимости от принятых условий (времени, 570 Пищевые системы значений параметров технического объекта и т. п.). Такой подход к управлению технологическим процессом расширяет возможность влиять на объект управления, что отличает его от классических систем, работающих в области четкой логики12. В рассматриваемом случае управляющее воздействие на объект управления (электромеханическую систему одностадийного измельчителя) следует формировать в зависимости от вычисленного прогноза температуры перерабатываемого мяса с учетом смежных границ температурных диапазонов, в которых структурномеханические свойства замороженного мяса могут иметь различные тенденции изменения своих значений.

Для моделирования работы ИСУ при формировании задания на установление режимных параметров процесса измельчения с применением адаптивной модели прогнозирования температуры замороженного мясного сырья разработали модель нечеткого управления. Для этой модели сформировали функции принадлежности входной и выходной переменных, а также базу правил. Входной переменной для модели является температура пограничного слоя мяса, прилегающего к зоне контакта с многолезвийным инструментом измельчителя. Предполагается, что конкретные значения указанной температуры определяются в результате аналитического расчета кратковременного прогноза с применением адаптивной модели, представленной выше. Нижняя граница в отрицательной области температур принята равной –8 оС, так как мясо считается замороженным при достижении данной или более низкой температуры13. Верхней границей в области положительных температур определили плюс 3 оС в случае предельного размораживания сырья, например, при длительном перерыве в работе технологической линии в условиях мясоперерабатывающего производства. Как показывает опыт одностадийного измельчения в лабораторных условиях, температура измельченного сырья находится в диапазоне –1,5 оС...–3,5 оС.

Для лингвистической переменной «температура» приняты следующие нечеткие терм-множества с соответствующими границами диапазонов: «отрицательная», «отрицательная малая», «нулевая», «положительная».

Выходной переменной нечеткой модели управления является частота вращения рабочего инструмента измельчителя, измеряемая в об/мин. Верхняя граница значений частоты вращения (2930 об/мин) определяется номинальной частотой вращения асинхронного короткозамкнутого электродвигателя привода механизма резания измельчителя. Нижняя граница частоты вращения определяется предельной малой частотой вращения режущего инструмента измельчителя для выработки тонко измельченного сырья, используемого в производстве колбасных изделий. В случае производства фарша для рубленых полуфабрикатов значение нижней границы диапазонов частоты вращения рабочего инструмента измельчителя может быть уменьшено.

Для лингвистической переменной «частота вращения» приняты следующие нечеткие терм-множества с соответствующими границами диапазонов: «малая», «средняя», «максимальная».

Для функций принадлежности входной и выходной переменных модели выбраны трапециевидная (trapmf) и треугольная (trimf) формы, которые следует отнести к кусочно-линейным функциям. Отметим, что в практике нечеткого моделирования такие функции используют для задания свойств множеств, которые характеризуют неопределенность вида: «приблизительно равно», «среднее значение», «расположен в интервале» и т. п. Таким образом, целесообразно использовать эти виды функции принадлежности для задания как температурных интервалов, так и интервалов изменения частоты вращения рабочего инструмента измельчителя.

На рисунках 6 и 7 приведены функции принадлежности лингвистических переменных «температура» и «частота вращения» для нечеткой модели.

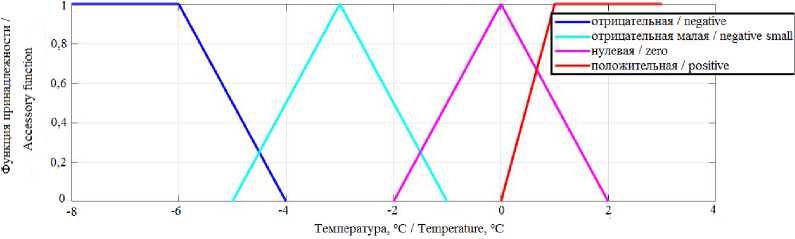
Р и с. 6. Терм-множества температуры пограничного слоя мяса F i g. 6. Therm-sets of the meat boundary layer temperature

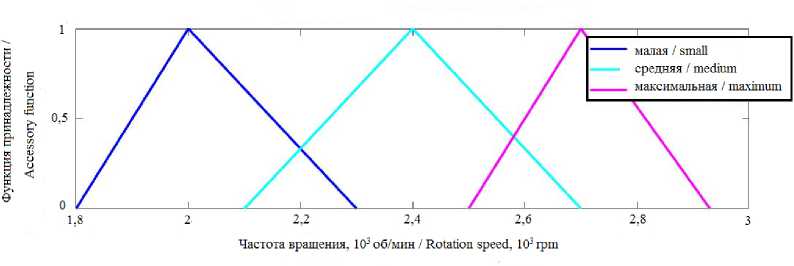
Р и с. 7. Терм-множества частоты вращения инструмента

F i g. 7. Term-sets of tool rotation speed

На рисунке 8 приведена схема модели.

Для нечеткой модели база правил составлена с учетом смежных (перекрывающихся) границ температурных диапазонов. Используется одна входная переменная «температура» и одна выходная переменная «частота вращения». Логическая взаимосвязь указанных переменных задается следующими правилами базы знаний:

• 1.    Если Т = «отрицательная» и Т = «отрицательная малая», то n = «малая».

• 2.    Если Т = «отрицательная малая» и Т = «нулевая», то n = «средняя».

• 3.    Если Т = «нулевая» и Т = «положительная», то n = «максимальная».

Отдельные условия в приведенной базе правил связаны между собой логической конъюнкцией (логическим «И»). Это позволяет учесть смежные границы температурных диапазонов, где могут быть расположены значения вычисленного температурного прогноза.

572                                                           Пищевые системы

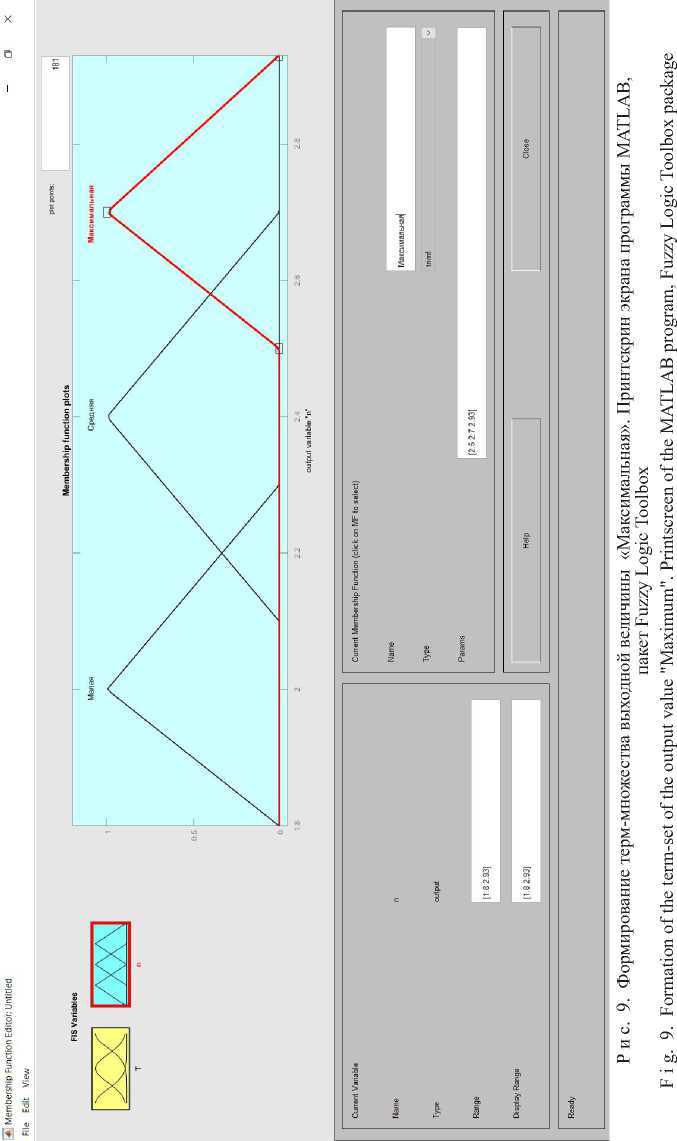
На рисунке 9 представлено формирование функции принадлежности терм-множества выходной величины «Максимальная».

Для моделирования принят алгоритм нечеткого вывода Э. Мамдани.

Дефаззификация выходной переменной нечеткой модели (частоты вращения многолезвийного инструмента измельчителя) проведена с использованием метода центра тяжести.

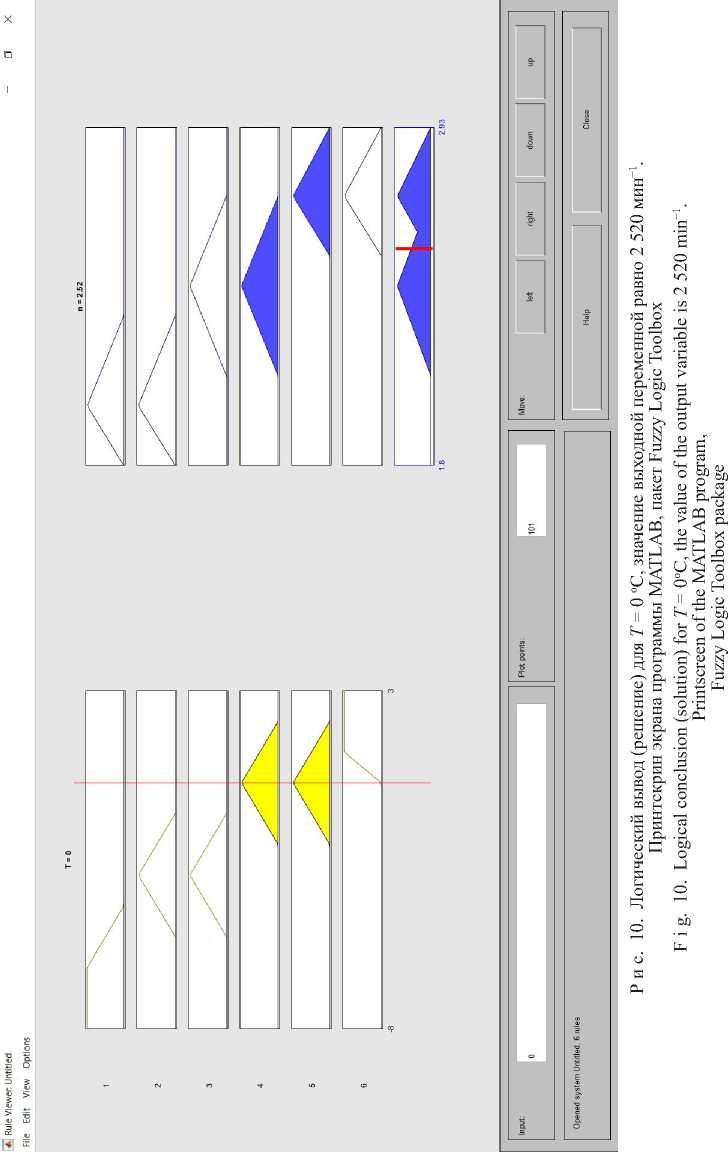
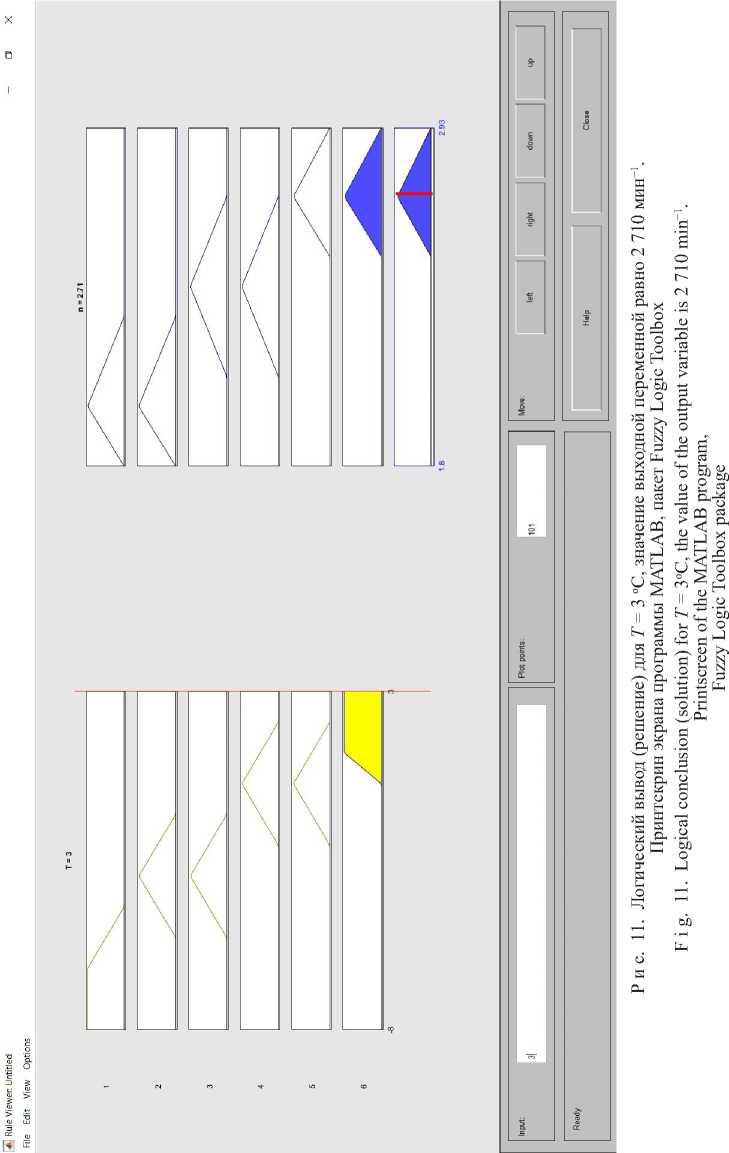
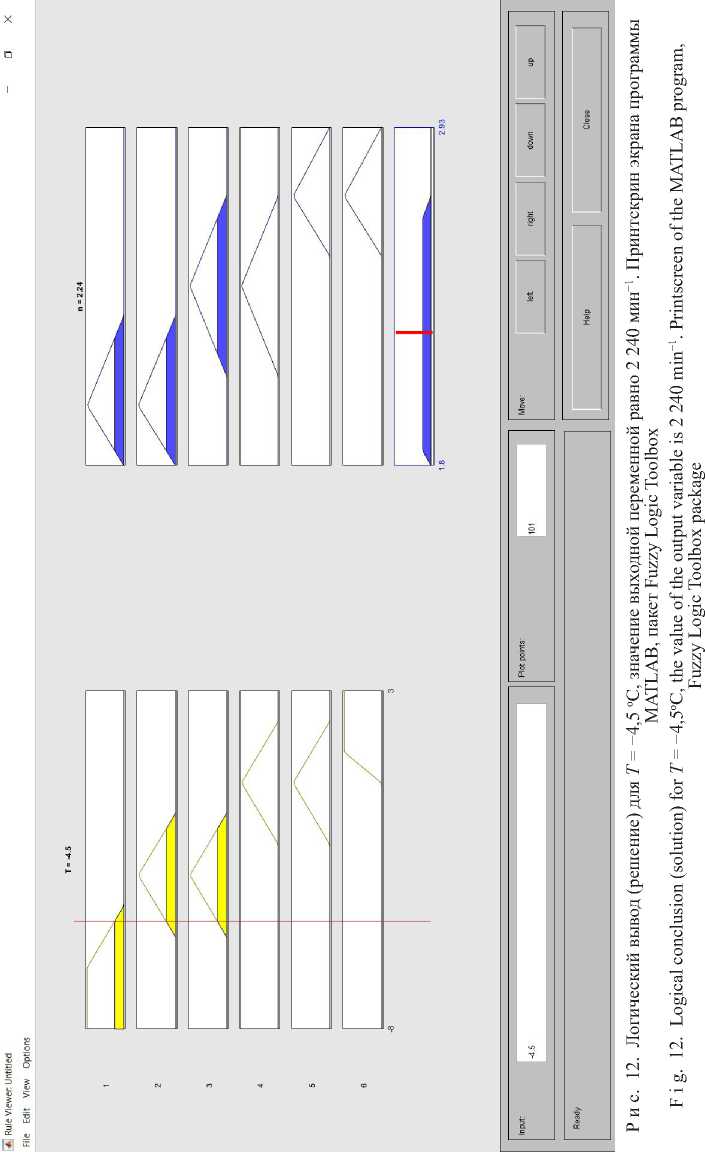
На рисунках 10, 11 и 12 представлены этапы реализации алгоритма логического вывода по Э. Мамдани для трех значений температурного прогноза. Как видно из результатов моделирования, конечным этапом во всех трех случаях является дефаз-зификация выходной переменной нечеткой модели температурного контроля сырья. В условиях функционирования технологической линии производства мясных продуктов полученные решения (результаты дефаззификации) будут являться заданием для исполнительных приводов одностадийного измельчителя, комплектующего линию.

На рисунке 10 представлен логический вывод (решение) для значения входной переменной Т = 0 оС (значение выходной переменной модели равно 2 520 мин-1), на рисунке 11 вывод для значения входной переменной Т = 3 оС (значение выходной переменной модели равно 2 710 мин-1), на рисунке 12 вывод для значения входной переменной –4,5 оС (значение выходной переменной модели равно 2 240 мин-1). Отметим, что в последнем случае значение температуры принадлежит двум терм-множествам («отрицательная» и «отрицательная малая») одновременно, то есть находится в смежной области соседних температурных диапазонов.

Так как база правил для нечеткой модели была составлена с применением логической конъюнкции («И»), компьютерная программа сформировала для используемой модели логический вывод (решение) для всего рассматриваемого температурного диапазона –8 оС...+3 оС (рис. 13).

Как видно из рисунка 13, чем выше значение (в градусах) прогноза температуры пограничного слоя мяса, тем большее значение частоты вращения рабочего инструмента (скорости резания) одностадийного измельчителя устанавливает компьютерное управление.

Функциональная схема температурного контроля (рис. 14) отражает структуру нечеткой модели управления, используемой в рассматриваемом случае.

Блок фаззификации (Fuzzification) вычисляет степень принадлежности ^ ( Т) прогноза температуры мяса определенному нечеткому множеству (терм-множеству) на температурной шкале. Вычисленное значение степени принадлежности поступает на вход блока формирования логического решения (блок логического вывода – Inference), который вычисляет результирующую функцию принадлежности выходного значения нечеткой модели. В рассматриваемом случае база¹⁴ правил должна отражать практический опыт одностадийного измельчения при различной температуре замороженного мяса, подтвержденный микроструктурными исследованиями полученного продукта. Блок дефаззификации (Defuzzification) на основе результирующей функции принадлежности вычисляет четкое числовое значение выходного параметра модели. Четким выходным параметром нечеткой модели температурного контроля сырья является скорость резания замороженного мяса, однозначно определяемая частотой вращения рабочего инструмента измельчителя. Задача контура управления (математической модели управления), работающего по законам четкой логики, заключается в том, чтобы свести к минимуму ошибку регулирования.

*w *--

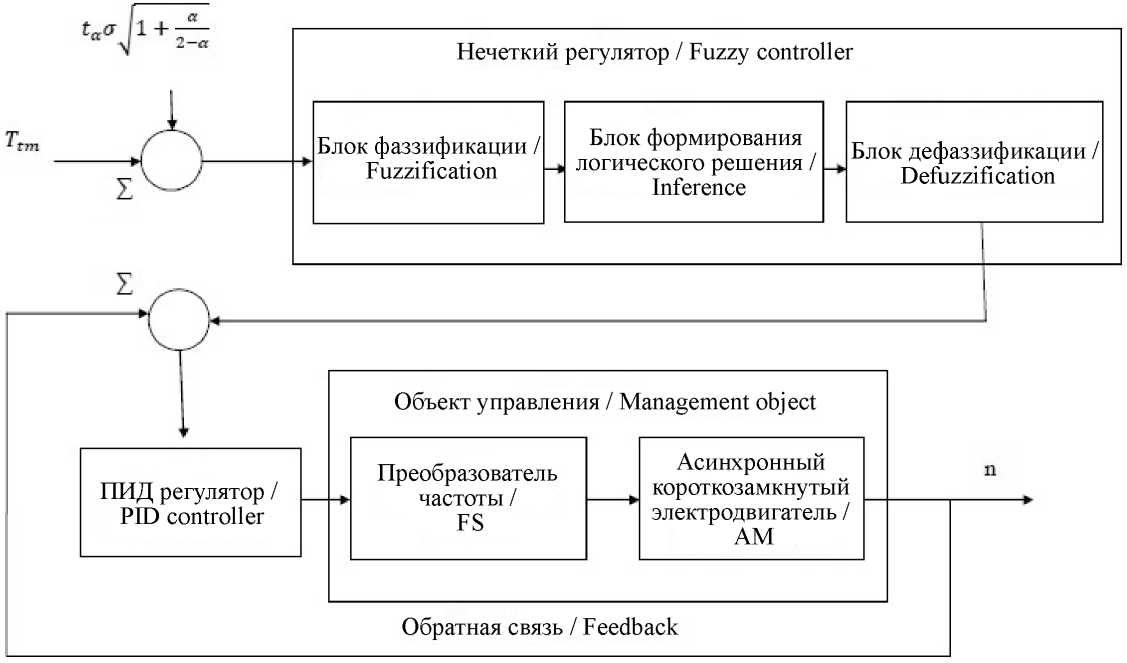
Р и с. 14. Функциональная схема температурного контроля

F i g. 14. Functional scheme of temperature control (PID controller – Proportional-integral-differential controller; FC – Frequency converter; AM – Asynchronous short-circuit motor)

В функциональной схеме температурного контроля (рис. 14) в качестве входной переменной нечеткой модели управления принято максимальное значение интервальной оценки температурного прогноза.

Обсуждая алгоритм функционирования предлагаемой системы температурного контроля, следует отметить его особенности в сравнении с традиционными техническими решениями в этой области. Системе придается функция непрерывного автоматизированного контроля температурного режима измельчения сырья под управлением промышленного компьютера. Это позволит уже на первом этапе переработки мяса обеспечить производство гомогенизированного измельченного продукта, что является обязательным условием получения высококачественной готовой продукции. Отметим, что на технологических линиях стандартной комплектации температура сырья контролируется на последующих стадиях его технологической обработки15.

Обсуждение и заключение

Реализация гибридного управления одностадийным измельчением замороженного мясного сырья в промышленных условиях функционирования технологической линии непрерывного действия производства мясных продуктов потребует расширения и уточнения условий базы правил для нечеткой модели управления. Это связано с различными температурными условиями хранения сырья в морозильных камерах мясоперерабатывающих производств. Очевидно, что при низких температурах хранения (например, –25...–30 оС) температурный диапазон изменения входной переменной «температура» нечеткой модели должен включать в себя указанные значения и далее по температурной шкале в направлении повышения температуры. Для выходной переменной нечеткой модели (частоты вращения многолезвийного инструмента измельчителя) в базу правил должны быть введены соответствующие входной переменной терм-множества с заданными функциями принадлежности. Используемая в приведенной выше нечеткой модели база знаний была сформирована для измельчения экспериментальных блоков замороженного мяса в лабораторных условиях.

Конечной целью температурного контроля сырья на первичной стадии его переработки является стабильность получения гомогенизированного измельченного продукта. Производство гомогенизированного по характерному размеру частиц продукта вследствие стабилизации степени измельчения сырья будет способствовать повышению качества готовой продукции, как это было указано выше. Однако результаты температурного контроля можно использовать и для дальнейшей технологической обработки измельченного мяса. В результате применения на первом этапе обработки сырья адаптивной прогностической модели контроля температуры мяса управляющий компьютер ИСУ может оценить температуру измельченного сырья в определенном его объеме, загружаемом в рецептурную мешалку. Используя полученную информацию и знания о химическом составе мяса, ИСУ может осуществить оптимальное сочетание всех ингредиентов фарша заданной пищевой ценности. Таким образом, предлагаемый температурный контроль может иметь многоцелевое назначение.

Выше отмечалось, что ИСУ процессом одностадийного измельчения, используя математическую модель, может рассчитать границы «коридора», в котором будет находиться размер получаемой мясной стружки с определенной доверительной вероятностью. Рассматриваемое гибридное управление позволит сделать эти расчеты более точными. Можно сказать, что управляющий компьютер «увидит» размер частиц, температуру, химический состав измельченного мясного сырья. Все указанные характеристики сырья искусственный интеллект рассчитывает без участия человека-оператора. Это дает возможность полностью автоматизировать дальнейшую технологическую обработку измельченного мяса с целью производства готовой продукции гарантированно высокого качества.