Применение неявной схемы разрывного метода Галеркина к решению задач газовой динамики на графических ускорителях NVIDIA

При численном решении многих задач газовой динамики и гидродинамики, необходимо учитывать процессы теплопроводности и диффузионные процессы. Как правило, данные задачи рассматриваются в областях сложной геометрической формы и их решение требуется находить с высоким порядком точности. Для того, чтобы при математическом моделировании учесть сложную структуру рассматриваемой области и как можно ближе приблизиться к ней, необходимо использовать неструктурированные сетки. Таким образом, для решения таких задач нужен численный метод, который бы обладал высоким порядком точности и при этом был хорошо адаптирован к неструктурированным сеткам. Одним из таких методов является широко известный метод Галеркина с разрывными базисными функциями (РМГ) [1–5]. Данный метод обладает целым рядом конкурентных преимуществ: характеризуется высоким порядком точности получаемого решения, слабо зависит от вида используемой расчетной сетки, что позволяет работать с неструктурированными сетками и при этом обладает компактным вычислительным шаблоном. Последнее означает, что для повышения порядка точности на каждом шаге вычислений данному методу требуются значения из текущей ячейки сетки и ее соседей по ребру. При всех перечисленных достоинствах РМГ требует существенных вычислительных затрат, что, при использовании явных схем, приводит к значительным временам расчета. Одним из перспективных направлений исследований является разработка эффективных неявных алгоритмов для РМГ на неструктурированных сетках. Несмотря на явные преимущества, предъявляет значительные требования к эффективному хранению СЛАУ в памяти и организации параллельных вычислений.

Данная работа посвящена разработке неявной схемы РМГ для решения уравнений газовой динамики на неструктурированных треугольных сетках. Численный алгоритм решения при таком подходе сводится к решению одной СЛАУ на каждом шаге по времени. Для параллельного исполнения этой операции на сегодняшний день разработано много эффективных решений для различных архитектур параллельного программирования. Но при этом стоит отметить, что неявная схема при всех ее достоинствах, имеет значительную сложность в реализации. Это связано с тем, что неявная схема требует существенно более сложного численного алгоритма, эффективного подхода при работе с памятью и особого внимания к матричным структурам, возникающим при выполнении расчетов.

На сегодняшний день в России и за рубежом активно ведется работа по созданию эффективных неявных схем РМГ [6–9]. Разработкой неявной схемы для РМГ применительно к решению уравнений Эйлера и Навье–Стокса на неструктурированных гексаэдральных сетках с использованием p-многосеточного метода рассмотрено в работе Волкова А.В. [10]. Серия работ посвящена построению явно-неявных схем РМГ для решения уравнений конвекции-диффузии [11–13].

В настоящий момент все более популярными становятся параллельные вычисления на устройствах GPU. Несмотря на то, что перенос алгоритмов на архитектуру графических процессоров, существенно отличающуюся от архитектуры центральных процессоров, представляет собой достаточно сложную задачу, GPU все чаще используются в вычислительной механике, задачах газовой динамики и в вычислительной математике в целом [14]. Благодаря своей архитектуре, основанной на большом числе вычислительных ядер, и новому подходу к организации вычислений, применение GPU в вычислениях является очень востребованным. Организация таких вычислений требует мощной, гибкой и при этом простой по своей логике технологии, которая бы дала возможность использовать все возможности GPU в уже существующих алгоритмах.

В представленной работе для решения СЛАУ используется библиотека NVIDIA AmgX, написанная на языке CUDA С. К достоинствам библиотеки следует отнести поддержку параллелизма как на уровне нескольких графических процессоров, так и на уровне нескольких вычислительных кластеров, что обеспечивается посредством поддержки технологии MPI. Также библиотека AmgX предоставляет гибкую систему конфигурации, и благодаря этому появляется возможность создавать иерархию решающих алгоритмов с произвольной глубиной, в которой внешний решающий алгоритм будет использовать внутренние в качестве предобработчиков и предобуслав-ливателей, которые сами могут быть обработаны другими методами. Такой подход позволяет пользователю быстро экспериментировать с различными схемами [15]. В настоящий момент библиотека находит все более широкое применение в современном промышленном и научном численном анализе. В частности, AmgX является составной частью коммерческого вычислительного программного обеспечения ANSYS Fluent [16]. Показателем актуальности и эффективности используемой библиотеки является и тот факт, что на данный момент она используется в качестве стандарта для сравнения эффективности и скорости работы новых численных алгоритмов для решения СЛАУ, наряду с такими мощными средствами как библиотека HYPRE [16].

Ранее авторы в работах [17, 18] разработали численную методику для неявной схемы метода Галеркина с разрывными базисными функциями применительно к ре- шению задач газовой динамики. В приведенных работах рассматривалась математическая модель без учета эффектов вязкости. Неявная схема записывалась в так называемой ≪дельта-форме≫, когда рассматриваются не сами искомые функции, а их приращения на каждом шаге по времени. Для решения итоговой СЛАУ применялись решатели из библиотеки HYPRE.

Данная работа продолжает ранние работы и расширяет их, рассматривая модель, учитывающую влияние эффектов вязкости. Для решения полученной на каждом шаге по времени СЛАУ применяются решатели из библиотеки NVIDIA AmgX.

1.    Математическая модель и вычислительный алгоритм

Рассмотрим двумерную систему уравнений Навье – Стокса, представленную в дивергентной форме:

∂ρ at+ d(Pu) + d(Pv) = 0 ∂x      ∂y     , (1) d(pu) ∂t + d(pu2 + p) + d(puv) - дтхх - дтху = . ∂x        ∂y     ∂x    ∂y     , (2) d(pv) ∂t + d(puv) + d(pv2 + p) - дтух - дтуу = 0 ∂x        ∂y       ∂x ∂y     , (3) dpE , d((pE + p)u) + d((pE + p)v) - д(тххu + Txyv) ∂t        ∂x           ∂y            ∂x д(тухU + Tyyv) _       z . dy             ,      ( ) где E = e + +— - удельная полная энергия, e - удельная внутренняя энергия, р - плотность, p - давление, v = (ux,uy) = (u,v) - вектор скорости, Tij (i,j = x,y) -компоненты тензора вязких напряжений.

Система замыкается уравнением состояния p = ре ( y — 1), где Y - показатель адиабаты, и дополняется начальными и граничными условиями, соответствующими постановке конкретной задачи.

Тензор вязких напряжений т = {T ij } определяется формулами

Tij = д ^ViUj + VjUi — 35ijVkuk^ ,i,j = x, y, где µ – коэффициент динамической вязкости, δij – символ Кронекера.

Для удобства дальнейших рассуждений введем следующие обозначения

U =

/ UA U 2 U \ UJ

ρ ρu ρv ρE

F ⁽²⁾ ( U ) =

, F = (F ⁽¹⁾ , F ⁽²⁾) , F ⁽¹⁾ ( U ) =

/ Ff»\

Ff \Ff/

ρu pu2 + p ρuv \ (pE + p)u)

_{F 1}(2)

_{F 2}(2)

Ff

_{F 4}(2)

ρv ρuv pv2 + p \ (pE + p)v)

, H = (H ⁽¹⁾ , H ⁽²⁾) ,

H ⁽¹⁾ ( U , W ) =

/ H , H ^u H*

\HJ

( 0 \ τ _xx τ _yx

\ Txx U + Txyv)

H ⁽²⁾ ( U , W ) =

_{H 1}(2)

_{H 2}(2)

H' \ H (

( 0 \ τ _xy τ _yy

\ Tyx U + Tyy v)

( WA   ( xxA

W 2 I = I T xy I , V • Q =

W3/   VuJ

/d 4lnl}   d 2 A\ x Uн+ y c 3 ^7

^d (Mv) + d ( m^u )

_v ^d < - I   ^{+ d} (I ^v),

Q = ( Q ⁽¹⁾ , Q ⁽²⁾ ), Q ⁽¹⁾ = m

( 4 \

3^u v 2

\ -1/

_{, Q} (2)

= M

( - 2 \

3v

u

\ Iv /

Дискретизация по пространству вязкого члена уравнений Навье – Стокса в методе Галеркина с разрывными базисными функциями [19] строится с помощью обращения к смешанной конечно-элементной формулировке. Производные первого порядка от консервативных переменных приводят к производным второго порядка, когда мы преобразуем дивергенцию вязких потоков. Однако производные второго порядка не могут быть согласованы напрямую в слабой вариационной формулировке, используя пространство разрывных функций. Следовательно, мы рассматриваем V- Q = W (U) как вспомогательные неизвестные уравнений Навье – Стокса [20], которые переформулируются в следующую сопряженную систему для неизвестных W , U и Q:

∂ U

-df + V- ( F ( U ) - H ( U , W )) = 0,

W = V • Q .

Для аппроксимации уравнений область Q G R ² , на которой ищется решение, покроем сеткой Q h = { K j | j = 1,..., N h } , состоящей из треугольных элементов таких, что Q = и ^ 1 K j , dim (K i П K j ) < 2, i, j = 1,..., N h ,i = j .

Введем пространство кусочно-полиномаиальных функций

VhK = {v G L2 (Q) : v|Kj G Pk (Kj) ,j = 1,..., Nh} , где PK (Kj) - пространство полиномов степени не выше чем K на элементе Kj.

Зададим в V hK базис ^ jk (x, y ) =

^aIt) k (yAyr)ek, если (x,y) G Kj, 0, в противном случае, где ak + ek < K,k = 1, • • •, N, N = (K + 1) (K + 2) /2, (xcj,ycj) - координаты центра масс ячейки, а Axj-, Ayj- - характерные размеры ячейки.

Дискретный аналог системы (5), (6) получаем, полагая, что внутри каждого эле- мента Ki сетки приближенное решение Uih , Qih и Wih представляется в виде:

N φ                             N φ                            N φ

U ih (t, x )= ^2 U ik (t)^ ik ( x ), Q ih (t, x )= 52 Q ik (t^^ ik ( X ), W ih (t, x )= 52 W ik (t)^ ik ( x ).

k =1                               k =1                              k =1

Применяя формулу интегрирования по частям, получаем:

Г ^Ф ^dU ik              Л^у.

/ ~tdT ik vV il ^dS + Ф (^Fn

K i ^{k =1}                  dK i

-

H n) V il da -

- У ( F ( U ih ) - H ( U ih , W ih )) • ^ V ti dS = 0, l = 1,...,N h ,

K i

N φ

£

K i ^k =1

W ik V ik V il dS - У Q П Vu da + J Q i? • ^V u dS = 0,l = 1-...-N ф ,

∂K i

K i

z где Fσn

z              z

= F " • n , H n

Z

Z

Z

= U • n , Q' = Q

^σ · n – функции потока, которые будут

определены ниже.

Заменим производную -—ik дискретным аналогом и с учетом шага по времени At перепишем систему в виде:

N φ / £ К_г ^k =1

U m ⁺¹ ik

-

At

U m V ik V il dS + / ( F ; ) ^{m +1} V il da - / (U ; ) ^{m +1} V _li da -

∂K i

∂K i

- / (f°> ( U ih⁺¹ )^ddx ^l + F ^|2) ( U m⁺¹ )dVyl) dS +

. w ¹ d) + h ⁽²⁾ ( u m⁺ⁱ , w . ■ ^dA) dS= 0,1 = 1,..., n , . (7)

+

K i

N φ

/ £ W ’’*¹ V ,_i V il dS - / (Q " ) ^{m +1} V il da+

K i ^{k =1}                     dK i

+ / ( q ' ,¹/ ( U ih⁺¹ ) ^ddjX ⁱ + Q h ( U m⁺¹ ) ^ddy- ) dS = 0, l = 1,..., N ф . K i

Далее рассмотрим нахождение элементов результирующей матрицы от конвективных слагаемых системы (7)

| a )

F ^{| a )} (U m⁺¹) = F ^{| a )} ( U i?. ) + "5 U- (U i?⁺¹ - U i?) , a = 1,2.

Введем обозначения:

A = f^ F -r)      - A = LЛR . Л = Л ^- + Л ⁺ , Л ^- =1( Л -| Л | ), Л ⁺ = ¹ ( Л + | Л | )

\ ^dU / и = и                                ^{2                2}

A = A- + A+, A- = LЛ-R, A+ = LЛ+R, A(1) = A|n=a,o), A(2) = A|n=(o,1), где R, L – матрицы, составленные из правых и левых собственных векторов матрицы A, л – диагональная матрица, составленная из собственных значений матрицы A, U соответствует решениям задачи о распаде произвольного разрыва. В работе используется потоковая функция Годунова [21].

Рассмотрим нахождение элементов результирующей матрицы от диффузионных слагаемых системы (7). Введем обозначения: G ¹ = dd u nn , G ¹⁽¹⁾ = G ¹ | _n =(io) , G ¹⁽²⁾ = G 1 | n =(o , 1) , G ² = a w n , G ²⁽ . = G ² | n =(1 , 0) , G ²⁽²⁾ = G ² | n =(0 , 1).                     '

Потоковые значения от конвективных и диффузионных слагаемых системы (7) с учетом введенных ранее обозначений находятся в виде: ( F n ) ^{m +1} = ( F n ) ^m + A + ( U m⁺¹ — u m ) + A - ( U m +1 — U m, ), ( HH ; ) ^{m +1} = ( H ; ) m + g ¹⁺ ( u m⁺¹ — U m ) + g ^{1 -} ( U m« — U mh ) + + G ²⁺ ( W m⁺¹ — W m ) + G ^2- ( W m⁺¹ — W m) , где G ^1- = G u u m _w = _w _ , G ¹⁺ = jh ^,        jh

1                       2 -        2                       2+       2

^G | ^u = ^u m ^{, w} = ^w m ^{, G G l u} = ^u7 ^{, w} = ^w m ^{, G G} | ^u = ^u m. ^{, w} = ^w m ^.

Для нахождения значения ( F n ) ^m в работе используется потоковая функция Годунова. Значение ( Н П ) ^т находится как среднее между двумя поверхностными состояниями: ( H n ) ^m = 2 (( H n ) m + ( H _n )^m). Нормаль n к ребру а направлена из ячейки с индексом i в ячейку с индексом j .

Рассмотрим нахождение элементов результирующей матрицы от диффузионных слагаемых системы (8). Введем обозначения: I ¹ = ^ Qu n , I ¹⁽¹⁾ = I ¹ | _n =(₁ , o) , I ¹⁽²⁾ = I ¹ | n =(0 , 1) ^.

Потоковые значения от диффузионных слагаемых ищем в виде ( Q n ) ^{m +1} = ( Q ; ) m + i ¹⁺ ( u m⁺¹ — u m ) + 1 ^1- ( u m⁺¹ — u m ), где I ^1- = I ¹ | _u = u , , i ¹⁺ = I u u. .

jh                      ih

Значение ( Q П ) ^m находится как среднее между двумя поверхностными состояниями: ( Q n ) ^m = 2 (( Q n ) m + ( Q n ) m) . Нормаль n к ребру а направлена из ячейки с индексом i в ячейку с индексом j .

Обозначим за rj границу между ячейками с индексами i и j. Введем в рассмотрение приращение за шаг по времени от решения AUmh+1 и вспомогательных переменных AWim+1, AQ. ■ ■ AU А = Ui,+ — Um, AWmh+1 = W А — Wm, AQ A = Qm+1 m ih      Qih.

Приращения искомых функций будем искать в том же пространстве базисных функций, что и сами функции: A U mh⁺¹ = ^ N =1 A U mm⁺¹ ^ ik , A W mh⁺¹ = TN* AWm"':„. AQm ⁺¹ = yN* AQm⁺¹^_fc. k =1 ik r ik , ^Vih        A^k =1 ^*ik r ik ^.

Полученную СЛАУ в ≪ дельта-форме ≫ решаем с использованием решателей из библиотеки NVIDIA AmgX.

Для подавления нефизичных осцилляций используется лимитер Кокбурна [19]. Как показано в работах [22, 23] при использовании линейных базисных функий лимитер Кокбурна показывает порядок точности 1,5 – 2,2 на гладких решениях. Для получения представленных ниже результатов расчетов использовались линейные базисные функции.

2.    Результаты расчетов 2.1.    Используемые вычислительные средства и библиотеки

Для проведения вычислительных экспериментов использовался персональный комьютер с процессором Intel Core i5-8265U и видеокартой NVIDIA GeForce MX250. Ниже представлены результаты, полученные с использованием решателей СЛАУ FGMRES и PBICGSTAB, реализованных в библиотеке AmgX версии 2.1.0.131-opensource. За среднее время выполнения одной итерации в расчетах ниже бралось общее время расчета всей задачи, поделенное на общее количество шагов по времени.

Для построения геометрических моделей и сеток использовался свободно распространяемый конечно-элементный генератор сетки Gmsh.

• 2.2.    Течение невязкого сжимаемого газа в плоском канале с клином

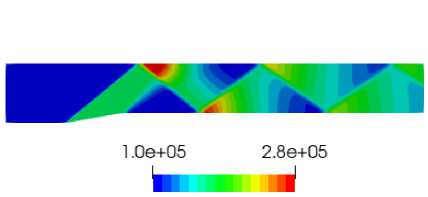
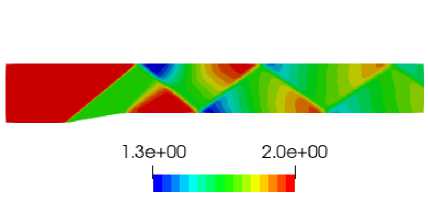
  Был выполнен расчет течения невязкого сжимаемого газа в плоском канале с клином при М=2 с числом Куранта, равным 5. Угол клина в канале равен 10 ° . Моделировалась конфигурации системы скачков уплотнения возникающих при обтекании начального клина и многократного отражения начального скачка от стенок канала при условиях: р ^ = 10 5 Па, Т ^ = 300 К, c v = 724,4 Дж/(кг К) [24]. В эксперименте была использована неструктурированная треугольная сетка, состоящая из 17096 ячеек. Слева было задано граничное условие входного потока, справа ставилось граничное условие выходного потока. На верхней и нижней стенках – граничное условие стенки без прилипания. Были выполнены расчеты с использованием решателей FGMRES и PBICGSTAB. На рисунке 1 представлены картины распределения поля давления и поля числа Маха в расчетной области для расчета с использованием решателя FGMRES. Результаты согласуются с результатами, полученными с использованием метода конечных объемов на блочно-структурированных [24, 25] и неструктурированных сетках [26].

а)

Рис. 1 . Распределение полей давления (а) и числа Маха (б), полученные с использованием решателя FGMRES

б)

Оба решателя сходятся примерно за 4000 итераций. Среднее время выполнения одного шага по времени представлено в табл. 1.

Таблица 1

Сравнение производительности решателей

Решатель СЛАУ FGMRES PBICGSTAB

Среднее время одного шага по времени, с 1,98 1,51

• 2.3.    Обтекание профиля NACA0012 дозвуковым потоком газа

  Был выполнен расчет течение вязкого сжимаемого газа в окрестности аэродинамического профиля NACA0012 с числом Маха M = 0, 7 под углом атаки 1,49 ° и числом Куранта, равным 5. Использовалась треугольная сетка, состоящая из 9902

ячеек. Характеристический размер ребра на границе профиля порядка 10 ^-3 . Слева, сверху и снизу было задано граничное условие входного потока, справа ставилось граничное условие выходного потока. На границе профиля – граничное условие стенки с прилипанием.

Выполнены расчеты с использованием решателей FGMRES и PBICGSTAB. Полученные численные результаты согласуются с результатами, полученными с использованием метода конечных объемов на блочно-структурированных сетках [26] и с экспериментальными данными [27]. На рис. 2 представлено распределение поля давления возле профиля, а на рис. 3 представлено распределение числа Маха, полученные с использованием решателя PBICGSTAB.

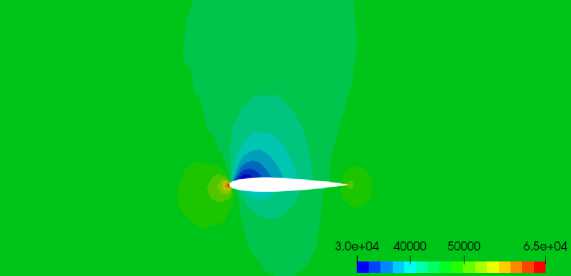
Рис. 2 . Распределение поля давления около профиля (PBICGSTAB)

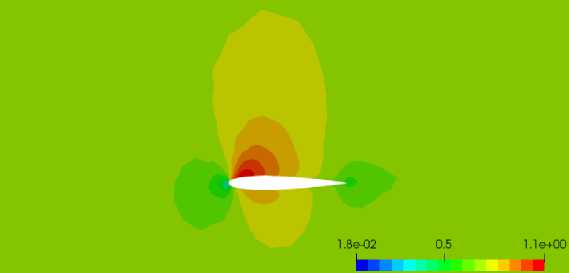
Рис. 3 . Распределение поля числа Маха около профиля (PBICGSTAB)

На рис. 4 представлено распределение коэффициента давления на поверхности профиля. Расхождение численных результатов и эксперимента на концах профиля можно объяснить тем фактом, что в численной схеме не учитываются турбулентные эффекты.

Численное решение с использованием решателя PBICGSTAB сходится примерно за 4000 итераций, при использовании решателя FGMRES решение сходится примерно за 5000 итераций.

В табл. 2 представлены средние значения времени выполнения одного шага по времени. Видно, что решатель PBCGSTAB демонстрирует лучшие результаты.

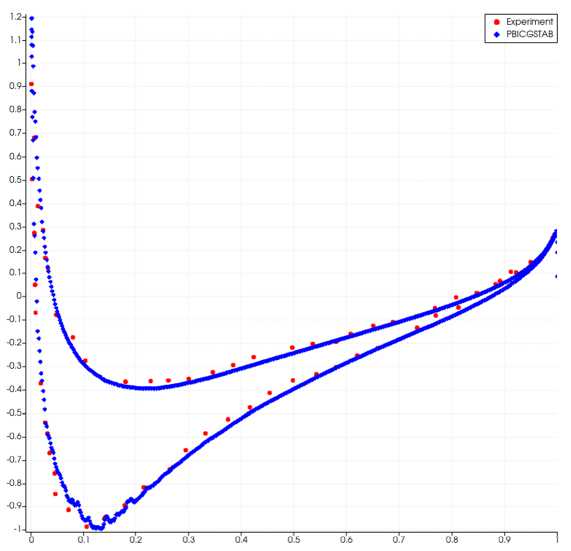
Рис. 4 . Распределение коэффициента давления на поверхности профиля в неявной схеме разрывного метода Галеркина (PBICGSTAB) и в эксперименте (Experiment)

Таблица 2

Сравнение производительности решателей

Решатель СЛАУ FGMRES PBICGSTAB

Среднее время одного шага по времени, с 3,52 3,21

Заключение

В работе представлена численная методика на основе неявной схемы разрывного метода Галеркина для решения двумерных уравнений газовой динамики на неструктурированных треугольных сетках. Для решения СЛАУ использовались решатели из библиотеки NVIDIA AmgX. Оба рассмотренных решателя демонстрируют примерно равную производительность. В задаче об обтекании симметричного профиля NACA0012 дозвуковым вязким потоком газа лучшие результаты по сходимости демонстрирует решатель PBICGSTAB. Представленные результаты расчетов говорят о возможности использования разработанной численной схемы для моделирования двумерных задач газовой динамики на неструктурированных сетках. Для ускорения расчетов планируется использовать новый функционал библиотеки NVIDIA AmgX, который позволяет распределенно загружать матрицу. При этом каждый процессор будет работает со своей частью глобальной матрицы.

Работа проводилась при финансовой поддержке гранта Российского научного фонда (проект № 19-71-00131).