Применение широкодиапазонного уравнения состояния смеси к описанию поведения пористого железа и смесей, содержащих железо

Железо является одним из самых востребованных металлов. Оно используется при производстве стали и чугуна как основной компонент и входит в состав сплавов с другими металлами, что служит предпосылкой для тщательного наблюдения и изучения поведения материалов, в составе которых присутствует железо. Оно является главным конструкционным материалом, и это объясняет потребность моделирования поведения материалов из железа при различных формах нагружения. Само железо является довольно мягким материалом, поэтому его сплавляют с различными легирующими элементами для получения разнообразных сталей с заданными свойствами. Отсюда возникает необходимость использования какой-либо математической модели для описания поведения смеси при описании процессов, происходящих в материалах с содержанием различных веществ. Прежде чем описывать составные материалы, необходимо получить достоверные сведения о компонентах сложных материалов. С этой целью проводится исследование, посвященное получению параметров уравнения состояния для железа.

Железо является полиморфным материалом, известны четыре модификации железа, обозначаемые а , в , Y и ⁸ , причем первые три формы существуют при нормальных условиях. В данной работе не проводится детализация того, какая именно модификация железа используется.

Порошковые материалы вызывают всё больший интерес в промышленности и науке. Изучение поведения пористых смесей порошковых материалов, подвергнутых импульсному сжатию, вызваны необходимостью получения новых материалов, требуемых потребностями современного производства. Учитывая востребованность и разнообразие материалов, в состав которых входит железо, построение модели уравнения состояния, позволяющей достоверное описание поведения смесей, обеспечит решение различных практических задач.

Построение уравнения состояния вещества - это непростая задача, для ее решения при рассматривании конкретной физической системы используется какая-либо упрощенная математическая модель с ограниченной областью применения. Применяется следующий прием: из практических соображений выбирается вид уравнения состояния, а параметры этого уравнения устанавливаются путем сравнения экспериментальных и расчетных данных. Сложность описания смеси конденсированных веществ существенно возрастает. Цель настоящей работы состоит в исследовании возможности применения полученного ранее уравнения состояния смеси с коэффициентом Грюнайзена, зависимость которого от объема задается в логарифмической форме, и в подборе параметров уравнения состояния железа.

Бельхеева Р.К.                   Применение широкодиапазонного уравнения состояния смеси к описанию поведения пористого железа и смесей, содержащих железо

Математическая модель уравнения состояния

При математическом моделировании ударно-волновых явлений в качестве уравнения состояния твердых тел чаще всего используют уравнение Ми–Грюнайзена

P = Px + Pt ,                                   (1)

в котором упругая часть описывается уравнением Тета

Px = A ( p)p ) n — 1

тепловая состав-

ляющая описывается выражением P T = yp E T . Здесь p - плотность среды; p ₀ - параметр уравнения состояния (в случае сплошного вещества это его плотность при нормальных условиях); A, n - константы, характеризующие вещество; у - коэффициент Грюнайзена; Е_т - тепловая энергия. Для задания коэффициента сжимаемости A используют выражение A = c 2 р ₀ -п , где c ₀ – объемная скорость звука при нормальных условиях. Внутренняя энергия также представляется в виде суммы двух составляющих:

E = E_X+ E_T.                                   (2)

Упругая часть внутренней энергии E_X и упругая часть давления связаны зависимостью

E X = [ Р PY A P- тепловая часть энергии задается соотношением E_T = c v ( Т - Т₀ ) , где c v - удель-

J ро р ная теплоемкость; T - температура; T - начальная температура. Важным условием при получении уравнения состояния смеси, используемого в данной работе, являлось требование одинакового вида уравнений состояния как всех компонентов, так и смеси. Правомерность использования для воздуха уравнения состояния в данной форме показана в [1].

В данном исследовании пористое вещество рассматривается как многокомпонентная гетерогенная среда, поры которой заполнены воздухом. Поры изолированы, испарения твердого вещества не происходит, концентрация газообразного вещества вследствие действия ударной волны не изменяется. Величина начальной пористости вычисляется как отношение плотности сплош- ного вещества к плотности пористого вещества при нормальных условиях.

Согласно изложенным в [2] принципам построения модели взаимодействующих и взаимопроникающих континуумов для простых смесей, термодинамически равновесную среду можно рассматривать как единый континуум, в уравнении состояния которого учитываются свойства всех составляющих. Условиями равновесия считаются условия равенства давлений, температур и скоростей для всех компонентов Pi = Р, Ti = Т, и, = и, (где Pi, Tt, ui - давление, температура и массовая скорость компонента i соответственно; Р, Т, и - давление, температура и массовая скорость смеси соответственно). В подобных случаях считается, что уравнения состояния компонентов в среде такие же, как в свободном состоянии. В рамках этого метода в [3] описан способ построения уравнения состояния и получены выражения для параметров уравнения состояния смеси.

Предложенная в [4] зависимость коэффициента Грюнайзена от плотности в виде

Y = Г о ( Р оIf ) ) ^{1П( РР 0)                                       (3)}

позволяет адекватно отображать поведение коэффициента Грюнайзена как для сплошных, так и для высокопористых веществ, и расширяет диапазон его применимости на область пониженных плотностей.

В выражениях для вычисления параметров уравнения состояния смеси массовая концентрация (массовая доля) компонента x i вычисляется как отношение массы i -го компонента к массе смеси, под истинной плотностью компонента ρ_ii понимается масса i -го компонента в единице объема i -го компонента, индекс 0 относится к начальному состоянию:

RR

n = -43 R2

— 1, A = kA N

—

nR.         1

■R y ^{P 0} = R

A

X1/ n

1N )

■ Y0 = - (P0 B1 )h(P0B) B,., cv

где

N

R 1 = Z—

. 1/ ⁿ i

i =1 P ii 0 У ^{Р +} kA N

N

R 2= Z x^-i =1 P ii 0

( Р + kA N

| i kA N ^— A i

I                                                          , ni

N

R3= У x i=1 Pii 0

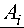
1/ n _i

< ^P + kA N у

⁽ ni+ 1 )

ni

kA N

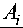
У

Величины A i упорядочены следующим образом: A 1 <...< A N . При значении коэффициента к, равном двум, выполняется условие сходимости для каждого ряда. Этот факт и способ получения выражений (4) описаны в [3]. Полученное уравнение состояния смеси удовлетворяет всем требованиям, сформулированным в [5].

Чтобы получить более полную информацию о поведении материалов при высоких температурах и должным образом описать полученное знание с помощью тепловой составляющей уравнения состояния, исследуют поведение пористых веществ, так как при интенсивных импульсных нагрузках возрастает доля теплового вклада в полное давление и полную энергию вещества. Изучению поведения пористых материалов в ударных волнах посвящено большое количество как экспериментальных [6–13], так и теоретических [14–17] работ. Методы исследования термодинамических свойств веществ и требования, предъявляемые к уравнениям состояния, описаны в [18, 19]. Сведения о свойствах материалов находятся в результате сопоставления экспериментальных данных и данных, полученных в результате математического моделирования ударноволновых явлений.

Соотношения Гюгонио для находящейся в покое в невозмущенном состоянии среды исполь- зуются в виде:

^р 00 ⁽ D - u 0 ) = ^{р (} D - u ),

P - P o = P oo ( D - u o )( u - u o ),   E - E ₀ =

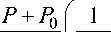
² I ^p oo

1 " p у

Здесь p ₀₀ , E 0 - соответственно плотность и энергия смеси перед фронтом ударной волны; и , P , E - массовая скорость, давление и энергия среды за фронтом ударной волны; D - скорость фронта ударной волны. Давление в среде перед фронтом ударной волны принимается равным нулю. Решение системы уравнений Гюгонио (5), дополненное уравнениями состояния среды (1)– (3) с параметрами (4), при заданном значении массовой скорости за фронтом ударной волны, определяет значения всех искомых величин за фронтом ударной волны.

Параметры уравнений состояния железа, меди и воздуха, которые использовались при проведении расчетов, указаны в таблице. При проведении расчетов были использованы одни и те же параметры уравнения состояния для всех значений пористости. Способность используемого уравнения состояния (1)–(3) описывать поведение материалов устанавливалась сравнением опытных и расчетных данных.

Параметры уравнений состояния воздуха, железа и меди

Вещество	P ii 0 , кг/м 3	Ai , Па	n i	C vi , кДж/ ( кгх К )	Y i 0
Воздух	1,3	0,695 - 10 - 3	2,20	0,718	0,16
Железо	7,873 - 10 3	3,153 - 1010	4,3	0,465	1,75
Медь	8,93 - 103	3,295 - 1010	4,25	0,382	2,00

Сравнение с экспериментальными данными

На рис. 1–2 приведены расчетные ударные адиабаты сплошных образцов железа в координатах «массовая скорость за фронтом ударной волны–скорость фронта ударной волны» и «плотность–давление за фронтом ударной волны». Экспериментальные данные, отмеченные символами, либо лежат на расчетных кривых, либо примыкают к ним для всего диапазона давлений и плотностей. Достигнутое хорошее соответствие расчетных и экспериментальных данных в широком диапазоне давлений показывает, что приведенная в работе математическая модель уравнения состояния очень хорошо описывает поведение железа в ударной волне. Использование логарифмической зависимости от плотности коэффициента Грюнайзена (3) позволяет расширить диапазон применения уравнений состояния (1)–(3), достигая достоверного качественного и количественного описания результатов эксперимента. Кроме того, показатель в случае сплошного вещества в зависимости (3) уменьшается с увеличением интенсивности нагружения, что дает более плавное изменение адиабаты.

Бельхеева Р.К. Применение широкодиапазонного уравнения состояния смеси к описанию поведения пористого железа и смесей, содержащих железо

В ударно-волновых экспериментах наиболее точными и надежными являются измерения массовой скорости за фронтом ударной волны и скорости ударной волны. Остальные параметры ударной волны находятся при подстановке этих скоростей в уравнения Гюгонио. Рис. 1 и 2 для сплошного железа показывают хорошее совпадение как измеряемых величин u и D , так и величин ρ и P , полученных с помощью использования соотношений Гюгонио.

20 -ж

D,

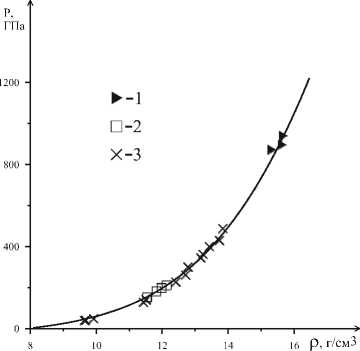
Рис. 2. Ударные адиабаты в сплошных образцах железа в координатах р - P ; расчетная кривая - сплошная линия; экспериментальные данные:

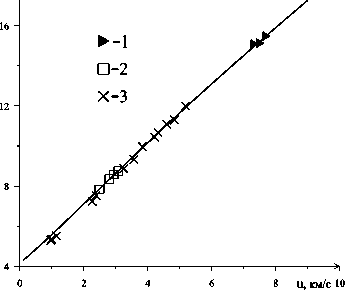
Рис. 1. Ударные адиабаты в сплошных образцах железа в координатах u - D ; расчетная кривая - сплошная линия; экспериментальные данные:

1 – [20] , 2 – [21], 3 – [22]

1 – [20] , 2 – [21], 3 – [22]

Более полное представление о том, как предлагаемая модель уравнения состояния (1)–(3) с параметрами, приведенными в таблице, описывает поведение конденсированного вещества, дает изучение данных, полученных с его помощью в области пониженных плотностей, т. е. при адиабатическом расширении. С этой целью рассмотрено поведение сплошных образцов при изоэнтропической разгрузке из конечного состояния материала, подвергнутого ударно-волновому сжатию. Для этого приводятся выражения для изоэнтропы разгрузки и скорости звука в рассматриваемом веществе. Основное уравнение термодинамики dS = dE/T + Pdv / T, где S – энтропия, v – удельный объем, в случае постоянной энтропии преобразуется к виду ln

cv ( T - T0 ) V Yv) v Ч ( Tin — T0 ) J1J  v in                 vin

Индексом in отмечены величины в исходном состоянии, в котором энтропия S = Sin . В случае постоянной удельной теплоемкости cv= cv  температура и плотность на изоэнтропе связаны соотношением:

( T - T o ) ( T n — T o )

= e

Y 0

to

ZH)n

n = 0

n !(2 n + 1)

2 n + 1

ln ^P

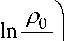
2 n + 1

P o )

v   P in )

Интеграл был вычислен путем разложения подынтегральной функции в ряд Тейлора.

Для более детального подтверждения адекватности предлагаемой модели проведено сравне- ние со всеми имеющимися экспериментальными данными. Скорость звука Cз2в

( d P )

— I опреде-

V^d P ) _s

ляет изоэнтропическую сжимаемость вещества. Для данной модели уравнения состояния с коэффициентом Грюнайзена в форме (3) выражение для скорости звука имеет вид:

C s ² = P

n ( P X + A ) + | у + 1 + 2ln ^ 0- I P_T

Результаты сравнения расчетных и экспериментальных

скоростей звука в координатах «массовая скорость за фронтом ударной волны – скорость звука на ударной адиабате», приведенные на рис. 3, также показывают хорошее совпадение.

Для образцов сплошного железа изоэнтропы в координатах «скорость свободной поверхности - давление», рассчитанные с использованием выражения (6), изображены на рис. 4 разрывными линиями, сплошная линия - адиабата Гюгонио. Экспериментальные точки либо совпадают, либо очень близко прилежат к расчетным кривым как для давлений начала изоэнтропической разгрузки порядка 100 ГПа (кривая 1), так и для давлений 200 ГПа (кривая 3). Хорошее совпадение результатов расчетов для сплошного железа с имеющимися на данный момент экспериментальными сведениями подтверждает надежность предлагаемого уравнения состояния железа при моделировании ударно-волнового нагружения и изоэнтропической разгрузки.

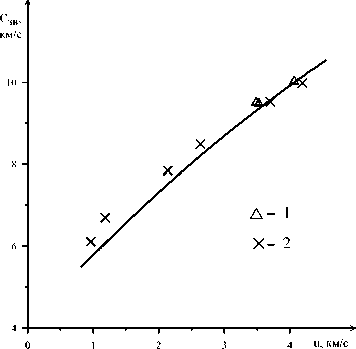
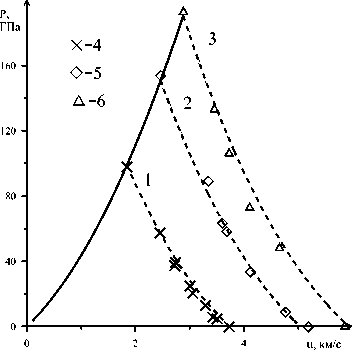
Рис. 3. Скорость звука на ударных адиабатах в сплош-   Рис. 4. Сплошная линия – адиабата Гюгонио, прерыви- ных образцах железа в координатах u - C3G ; экспери-   стые линии - адиабаты Пуассона в сплошных образцах ментальные данные: 1 - [23], 2 - [24]           железа в u -P -координатах; экспериментальные дан ные: 4, 5– [25] , 6 – [22]

Представление о зависимости свойств материалов от высоких температур получают, подвергая ударному обжатию образцы одного и того же материала при различных начальных пористостях. Анализируя полученные в результате экспериментов данные, устанавливают зависимость коэффициента Грюнайзена от температур и плотностей в широком диапазоне давлений. Начиная с некоторых пористостей наклон ударных адиабат изменяется: при возрастании давлений объем среды пористых материалов увеличивается, в то время как в сплошных материалах объем уменьшается. Такое поведение адиабат пористых материалов называют аномальным. Случай аномального поведения ударных адиабат не отражается при использовании общепринятой зависимости коэффициента Грюнайзена, описываемого формулой у = у ₀ ( р ₀ \ р ) l , где l >  0. Применение этой зависимости для описания коэффициента Грюнайзена при моделировании импульсных нагружений для материалов с высокой пористостью приводит к тому, что коэффициент Грюнайзена возрастает с ростом интенсивности ударной волны. Это противоречит наблюдениям. В [3] показано, что в случае высокой пористости образца для адекватного отображения расчетных ударных адиабат необходимо показатель задавать отрицательным числом l <  0. В предлагаемом варианте описания коэффициента Грюнайзена в форме (3) знак показателя зависит от величины аргумента логарифма и при р / р ₀ <  1 показатель становится отрицательным. Предложенное уравнение состояния с коэффициентом Грюнайзена в виде (3) позволяет описать аномальный ход адиабат в области пониженных плотностей, что демонстрируют рис. 5 и 6.

На рис. 5 и рис. 6 приведены ударные адиабаты образцов железа различной пористости в координатах «массовая скорость за фронтом ударной волны - скорость фронта ударной волны» и «относительная плотность - давление за фронтом ударной волны». Рядом с кривыми указаны соответствующие значения пористостей образцов, через рт0 обозначена плотность сплошного железа при нормальных условиях. Рис. 5 демонстрирует близкое прилежание измеряемых в эксперименте величин и и D к расчетным кривым для образцов со всеми приведенными пористостями, что показывает хорошее описание поведения среды предлагаемым уравнением состояния. На рис. 6 наиболее сильно от расчетных кривых отклоняются экспериментальные точки для образцов железа с пористостью, равной двадцати. Это различие может быть вызвано неучетом при моделировании ударно-волнового нагружения физико-химических процессов, происходящих при сильном нагревании образцов железа. По расположению экспериментальных точек (излом на экспериментальной адиабате) для образцов железа с пористостью, равной десяти, можно сделать заключение о происходящем при давлениях порядка 20 ГПа полиморфном фазовом переходе. Для образцов железа с пористостью, равной m = 1,66, экспериментальные точки расположены почти вертикально, и это описывается предложенным уравнением состояния. Следует учесть, что использовались одни и те же параметры уравнения состояния для всех значений пористостей. Хорошее совпадение расчетных и экспериментальных данных для различных значений пористо- сти подтверждает правомочность использования этой модели уравнения состояния.

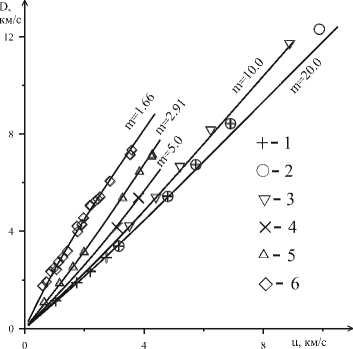
Рис. 5. Ударные адиабаты в пористых образцах железа в координатах u - D ; экспериментальные данные: 1 – [26], 2, 3, 4 – [27], 5 – [28], 6 – [29]

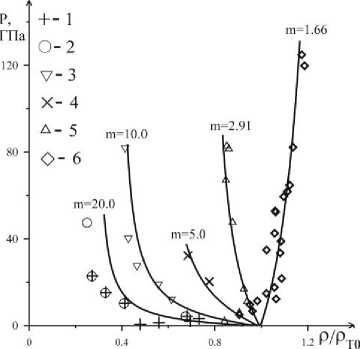
Рис. 6. Ударные адиабаты в пористых образцах железа в координатах р / р _го - P ; экспериментальные данные: 1 – [26], 2, 3, 4 – [27], 5 – [28], 6 – [29]

Далее на рис. 7 и рис. 8 проведено сравнение расчетных и экспериментальных ударных адиабат для смеси железа и меди с массовыми концентрациями железа и меди 0,49 и 0,51 соответственно. В работе [4] проведено исследование применимости аналогичной модели уравнения состояния и получены параметры для описания меди. Экспериментальные данные приведены для сплава. В расчетах сплав рассматривается как смесь с пористостью, равной единице (m = 1). Ударная адиабата смеси железо–медь находится между ударными адиабатами железа и меди. Ре- зультаты расчетов демонстрируют удовлетворительное совпадение расчетных и эксперименталь- ных данных в пределах точности экспериментов.

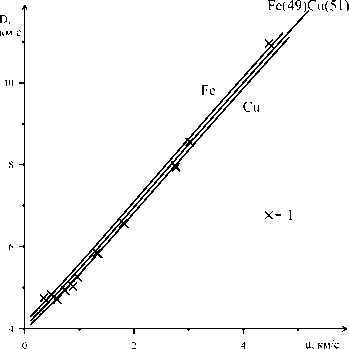
Рис. 7. Ударные адиабаты в сплошных образцах железа, меди и смеси железо–медь в координатах u - D ; экспериментальные данные: 1 – [30]

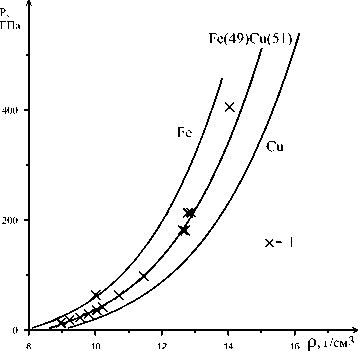
Рис. 8. Ударные адиабаты в сплошных образцах железа, меди и смеси железо–медь в координатах ρ - P ; экспериментальные данные: 1 – [30]

Выводы

Полученные результаты свидетельствуют о возможности описания предлагаемым уравнением состояния монолитных и пористых материалов для ударных сжатий и последующих разгрузок. Использование логарифмической зависимости коэффициента Грюнайзена позволяет расширить диапазон плотностей и описывать поведение вещества как в области разрежения на изоэн- тропе разгрузки, так и для образцов со значительной пористостью. Таким образом, предложенная простая модель уравнения состояния смеси, параметры которой определяются параметрами входящих в смесь составляющих и массовыми концентрациями компонентов, позволяет производить достоверные расчеты для пористых смесей. Показано, что эта модель адекватно описывает экспериментальные данные по ударно-волновому нагружению и адиабатической нагрузке образцов железа различной пористости и смеси железо–медь.