Применение технологии искусственного интеллекта в процессе повышения квалификации и активизации самообразовательной деятельности учителей математики

П остановка проблемы. В современных условиях курс на обеспечение высоких темпов роста национальных социально-экономических показателей Союзного государства требует выявления и мобилизации всех существующих ресурсов, важнейшим из которых является человеческий потенциал. При этом большое значение имеет система дополнительного образования взрослых, которая должна носить инновационный многовекторный характер. В XXI в. необходимы учителя, которые могут адаптировать содержание своей профессиональной деятельности к изменяющимся приоритетным запросам общества и государства. В Концепции развития системы образования Республики Беларусь до 2030 г.¹ указано, что «дополнительное образование взрослых становится основным связующим звеном между системой профессионального образования и рынка труда, обеспечивая непрерывную адаптацию выпускников учреждений профессионального образования к постоянно изменяющимся социально-экономическим условиям», при этом цель развития системы образования в контексте процессов цифровизации определена как «совершенствование национальной системы образования на основе развивающихся цифровых технологий, подготовка обучающихся к жизни в цифровом обществе».

В эпоху цифровизации и глобализации образование переживает трансформации, обретая новые высокоинтеллектуальные аспекты, включая внедрение различных цифровых инструментов, таких как нейросети, искусственный интеллект, GPT-чаты и другие технологии. В последние годы искусственный интеллект (далее – ИИ) все больше интегрируется в нашу повседневную жизнь, предоставляя социуму разнообразные возможности, улучшая качество жизни и способствуя самообразованию и самореализации. Сегодня можно с уверенностью сказать, что ИИ является сложным и

1 Концепция развития системы образования Республики Беларусь до 2030 г., утверждена Постановлением Совета Министров Республики Беларусь 30 ноября 2021 г. № 683.

многогранным феноменом, который вызывает значительные социокультурные изменения, как положительного, так и отрицательного характера, влияя на человека и человеческую цивилизацию в целом.

ИИ и машинное обучение в настоящее время активно используются в образовательной сфере для организации и проверки контрольных работ, тестов, экзаменов, автоматического подбора учебных материалов для обучающихся, в том числе для построения индивидуальной траектории обучения, выявления и ликвидации пробелов в знаниях и т.д. Вместе с тем 28 марта 2023 г. более 1125 ведущих специалистов в области IT, в том числе глава Tesla, SpaceX и Х Илон Маск, сооснователь Pinterest Эван Шарп и сооснователь Apple Стив Возняк, подписали открытое письмо с заголовком: «Мы призываем все лаборатории ИИ немедленно приостановить как минимум на 6 месяцев обучение систем ИИ, более мощных, чем GPT-4!». Авторы послания ставят следующие вопросы: «Должны ли мы позволять машинам заполнять наши информационные каналы пропагандой? Следует ли нам автоматизировать все рабочие места? Нужно ли развивать нечеловеческие интеллекты, которые в конечном итоге могут превзойти нас по численности, обмануть, сделать нас ненужными и заменить? Стоит ли рисковать утратой контроля над нашей цивилизацией?»2. Таким образом, возникает вопрос: если у руководителей лабораторий самого высокого ранга, занимающихся разработкой машинного обучения, возникают опасения в связи с развитием ИИ, то каково его влияние на функционирование системы дополнительного образования в целом и как ее неотъемлемой части, системы повышения квалификации и активизации самообразовательной деятельности учителей математики (далее – ПКиСД)?

Цель работы – определение направлений разрешения несоответствия между потенциально эффективными дидактическими возмож- ностями современных веб-ориентированных ресурсов как средств организации повышения квалификации и активизации самообразовательной деятельности учителей математики и отсутствием теоретически обоснованной, внутренне целостной и логически непротиворечивой дидактической системы реализации этих возможностей в практике дополнительного образования учителей.

Методология и методы исследования . В ходе исследования генезиса мы выделили ключевые этапы развития процесса повышения квалификации учителей математики за последние 150 лет, сосредоточив внимание на основных дидактических принципах, формах организации и методах представления учебного материала. Исследование показало актуальность задачи проектирования и разработки дидактической системы повышения квалификации и активизации самообразовательной деятельности учителей математики с использованием веб-ориентированных ресурсов [Прохоров, 2021]. В ходе работы использовался комплекс методов : изучение философской, психологопедагогической и методической литературы, сравнительный анализ учебных математических апплетов, анкетирование.

Обзор научной литературы . Проблеме научно-методического обеспечения профессионально-педагогического становления будущих учителей математики, последующему их сопровождению в процессе повышения квалификации, активизации самообразовательной деятельности, непрерывному повышению уровня их профессиональных компетенций и т.д. уделялось достаточно большое внимание. В Беларуси такие исследования проводили: Н.Б. Бровка [Бровка, 2009], М.В. Ильин [Ильин, 2002], А.В. Позняк [Позняк, 2022] и др., в России: Н.Ф. Ильина, А.С. Ильин, Е.Э. Хохлова [Ильина и др., 2020], Л.В. Шкерина, М.Б. Шашкина, О.А. Табинова [Шкерина и др., 2022] и др., в странах Западной Европы: М.В. Кларин [Кларин, 1995], J. Kotter [Kotter, 2005] и др.

Согласно Кодексу Республики Беларусь об образовании под повышением квалификации руководителей и специалистов мы понимаем процесс «реализации образовательных программ, направленных на профессиональное совершенствование работников»3. Анализ психолого-педагогической литературы показывает, что проблемы самообразовательной деятельности учителя в основном рассматриваются с двух позиций: как «самостоятельная деятельность педагога по повышению своих профессиональных компетенций» (В.А. Адольф, 2021) и как «индивидуально-личностный процесс целенаправленного и систематического улучшения, развития себя и своей деятельности» (Кулюткин, 2022). В данной работе мы сосредоточимся на первом подходе, так как второй предполагает исключительно личностный аспект самообразования учителя (как его саморазвития), что не отвечает направлениям нашего исследования.

Несмотря на тщательное изучение методологических, методических и управленческих аспектов поддержки будущих учителей математики в ходе их обучения и профессионального развития, в исследованиях не были рассмотрены особенности и структурные элементы процесса ПКиСД учителей математики, основанного на применении веб-ориентированных ресурсов.

Основу современной концепции развития системы ПКиСД учителей математики составляют цифровые технологии интернета, мобильные сервисы, технологии Web 2.0, 3.0, ИИ, предусматривающие активное участие пользователей в формировании в учреждениях образования учебного контента. На сегодняшний день защищен ряд кандидатских и докторских диссертация по философским4, онтологическим5,

социальным6, юридическим7 аспектам, методике обучения информатике8, в которых представлены исследования различных направлений внедрения технологий ИИ. В целом нейронные сети представляют собой математические модели и мощные вычислительные алгоритмы, которые способны прогнозировать, решая интеллектуальные задачи на основе оценки критериев заданного вопроса. Они анализируют обширные объемы информации и баз данных, что позволяет ИИ формировать наиболее точные и актуальные ответы на запросы в GPT-чатах. Одним из главных преимуществ нейросетей является их способность к самообучению, что позволяет им развиваться без необходимости постоянного вмешательства IT-специалистов в область машинного обучения [Абламейко и др., 2023; Фирсов и др., 2020; Markova et al., 2021]. Важность роли учителя математики не просто как источника знаний, но организатора процесса их передачи, использующего потенциал современных технологий, подчеркивается в аналитической записке Института ЮНЕСКО по информационным технологиям в образовании: «эффективное применение искусственного интеллекта, данных и аналитики, а также машинного обучения может сделать процесс обучения более увлекательным, используя технологии для погружения в виртуальную среду»9. Искусственный интеллект выполняет задачи по изучению и сопоставлению данных, предоставляя рекомендации ученикам для освоения материала и позволяя учителю математики анализировать результаты, что помогает отслеживать уровень подготовки каждого учащегося, корректировать его индивидуальную траекторию обучения, выявлять и ликвидировать пробелы в его знаниях.

Изучение исследований, касающихся проблемы использования образовательных сервисов интернета Е.Д. Патаракина [Патаракин, Яр-махов, 2021], S. Downes [Downes, 2024], Ed. Krol [Krol, 2022], T. Richardson [Richardson, John, 2023], J. Thompson [Thompson, 2021] и др., более чем пятнадцатилетний опыт проведения лекций и практических занятий, организации диалоговых площадок, научно-практических конференций и самообразовательной деятельности для учителей в ГУО «Минский городской институт развития образования», а также результаты анкетирования, в котором приняли участие 378 учителей математики, свидетельствуют о том, что современные педагоги проявляют интерес к систематическому повышению своей квалификации в сфере цифровых компетенций . Учителя математики осознают необходимость непрерывного самосовершенствования и самообразования в направлении повышения уровня знаний и способов деятельности по использованию ИКТ в повседневной и профессиональной деятельности, однако не имеют технического и методического инструментария. На вопрос «Какую форму представления информационно-обучающего ресурса Вы считаете наиболее эффективной в современных условиях?», 56 % – размещенный в интернете, 39 % – мобильные приложения, 5 % опрошенных учителей математики предпочитают ресурс, установленный на персональном компьютере. 83 % опрошенных учителей математики хотели бы повысить свои профессиональные компетенции и пройти повышение квалификации по теме «Дидактический дизайн в преподавании математики в учреждениях общего среднего образования».

Результаты исследования. Мы рассматриваем дидактическую систему повышения квалификации и активизации самообразовательной деятельности учителей математики с использованием веб-ориентированных ресурсов как «теоретически обоснованную, внутренне целостную и логически непротиворечивую систему, построенную на основе полипарадиг-мального подхода (взаимодополнение и вза-имообогащение положений синергетического, системно-деятельностного, праксеологическо-го, компетентностного, логистического, кон-нективистского, инструментального подходов в обучении) с учетом методических условий цифровой дидактики, общедидактических принципов (фундаментальности, гуманизации и гуманитаризации; опережающего характера обучения), дополненных принципами, обусловленными спецификой процесса повышения квалификации и самообразовательной деятельности учителей математики (партиси-пативности, фундирования, оптимальной информационной насыщенности), включающую взаимосвязанные цели, содержание, формы, методы, средства, веб-ориентированные ресурсы, контрольно-измерительный инструментарий определения эффективности обучения, функционирующую во взаимодействии преподавателя и слушателей для повышения уровня профессиональных компетенций учителей математики» [Прохоров, 2024, 32].

В данной статье мы рассмотрим технологический и методический аспекты взаимодействия учителей математики в рамках ПКиСД с веб-ориентированными ресурсами, созданными на основе мобильных технологий с применением элементов GPT-чата, а также ИИ. Но прежде необходимо дать ряд определений.

Мобильный учебный математический апплет (апплет от англ. applet, application – приложение и -let – уменьшительный суффикс) (далее – мобильный апплет) – учебно-методическое средство, являющееся составной частью веб-ориентированного ресурса и/или самостоятельное средство обучения, требующее установки на мобильный носитель (смартфон, планшет и т.д.), предоставляющее возможность как линейного, так и нелинейного изучения содержания, сочетающее символьный и графический способы представления материала и включающее динамическую модель математического объекта, краткий теоретический материал, а также диагностический инструментарий эффективности его усвоения. Мобильные апплеты – это программы, которые устанавливаются на операционные системы мобильных устройств, таких как Microsoft, iOS, Android и т.д. Они обеспечивают функционал для взаимодействия между пользователем и мобильным устройством, а также между пользователями. Эти апплеты позволяют реализовывать различные алгоритмы интерактивного взаимодействия участников образовательного процесса, включая использование технологий ИИ.

Искусственный интеллект (англ. artificial intelligence – AI) – способность цифровых компьютеров или контролируемых роботами компьютеров решать задачи, которые обычно связывают с человеческими¹⁰.

Веб-ориентированный ресурс обучения – гибкий и мобильный ресурс, который содержит учебно-методический и диагностический материал, коммуникационно-методический инструментарий, позволяющий в режиме реального времени обучающемуся выстраивать свою индивидуальную траекторию обучения (самостоятельно и/или под руководством преподавателя) [Прохоров, 2024, с. 31].

В ходе исследования нами проведен анализ востребованности педагогической общественностью содержательного, методического, учебно-методического, информационного и ресурсного обеспечения построения обучения математике учащихся II–III ступеней учреждений общего среднего образования на основе веб-ориентированных ресурсов, включающего мобильные апплеты и поддерживающего коммуникацию с ИИ. Интерес к таким разработкам со стороны пользователей интернета (по объективным причинам выделить среди них категорию «учитель математики» не представляется технически возможным) подтверждается динамикой популярности соответствующих запросов в интернет-поисковиках. Шкала частоты запросов, построенная на основе инструмента ИИ Google Trends ,

представлена виде графика динамики соответ- сти соответствующего запроса по отношению к ствующих обращений (рис. 1), где 100 баллов аналогичным в Республике Беларусь в периода означают самый высокий уровень популярно- с 01.01.2019 по 01.01.2025.

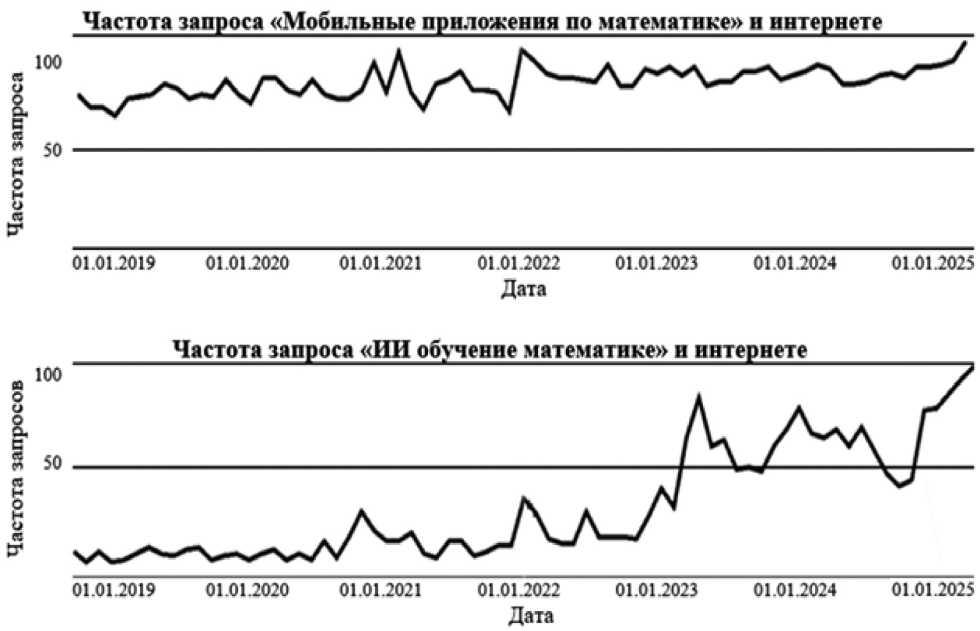
Рис. 1. Частота запросов в интернете по данным Google Trends

Fig. 1. Frequency of Internet queries according to Google Trends

Таким образом, на графиках четко прослеживается постоянный интерес пользователей интернета к мобильным апплетам, содержащим справочную информацию, позволяющим обрабатывать математические данные, решать математические задачи, учащимся проверять свои знания. Запрос общественности к возможностям использования ИИ в процессе обучения математике постоянно растет с конца 2021 г.

На сегодняшний день в русскоязычном сегменте интернета мобильных учебных приложений по математике для платформ Microsoft, iOS и Android насчитывается более 50. Анализ их содержания и качества представленного контента позволил классифицировать их по основным направлениям с точки зрения решаемых педагогических задач: математические справочники и тестовые среды, мобильные апплеты для решения математических задач, мобильные ма- тематические тренажеры и математические симуляторы. Наибольшей популярностью (рейтинг приложений в AppStore и GooglePlay выше 4,5 из 5,0) пользуются мобильные апплеты с математическим содержанием, которые представлены в табл. 1. Примечание: некоторые из представленных мобильных апплетов содержат рекламу, авторы статьи не являются разработчиками данных апплетов и не несут ответственности за их содержания. Содержание табл. 1 выполняет исключительно информационную функцию.

Следует отметить, что многие мобильные апплеты созданы на основе технологий нейросетей, в частности приложения для решения математических задач и математические симуляторы. Технология обработки текстовой, графической и мультимедийной информации нейросетями достаточно подробно описана У. Холмсом, М. Бялик, Ч. Фейделом [Холмс и др., 2022].

Таблица 1

Примеры мобильных учебных математических апплетов

Table 1

Examples of mobile educational math applets

Название	QR-од доступа	Описание
1	2	3
Математические справочники и тестовые среды
Математика: формулы + тесты	ВД®Л0 MS^R	Мобильный апплет предназначен для школьников и студентов, охватывает школьный курс алгебры, геометрии и начал анализа
Формулы по алгебре с тестом		Апплет содержит справочную информацию по алгебре, тестовые задания для проверки знаний учащимися формул
Учебники по математике	®^® ИВ	Приложение содержит пошаговые уроки по арифметике, алгебре, дробям, геометрии, тригонометрии и т.д.
Мобильные апплеты для решения математических задач
Photomath	BjS§re&B иЖО^	Приложение с помощью камеры мобильного устройства мгновенно сканируется печатный текст, разбивает решение на шаги
Mathway	®*^^1 в*ИЯ	Мобильный апплет предназначен для решения алгебраических задач, построения графиков, математического анализа

Окончание табл. 1

1	2	3
Maple Калькулятор: решатель	и&£ё&и	Приложение является универсальным калькулятором на основе Maple, решает математические задачи, визуализирует двухмерные и трехмерные графики выражений и предоставляет пошаговые решения
Мобильные математические тренажеры
Математика – игры для ума	^■^ Ж м	Апплет способствует развитию логического и математического мышления, содержит головоломки, тренажеры и тесты по математике
Мышление и логика для взрослых и детей	1ЙЙи	Приложение содержит более 1000 заданий, способствующих развитию логического мышления и пространственного воображения
Математические загадки	®!£Ж&&®	Тренажер позволяет закрепить навыки устного счета, арифметических вычислений задач, установления математических закономерностей
Математические симуляторы
GeoGebra	и^айжи г^Ж^	Мобильные апплеты, позволяющие проводить онлайн-вычисления арифметических, алгебраических и геометрических задач, содержат элементы 3D моделирования математических объектов

В. Юрченковым и Д. Кургановым проведен анализ ключевых этапов зарождения и развития алгоритмов машинного обучения, GPT-часов и ИИ

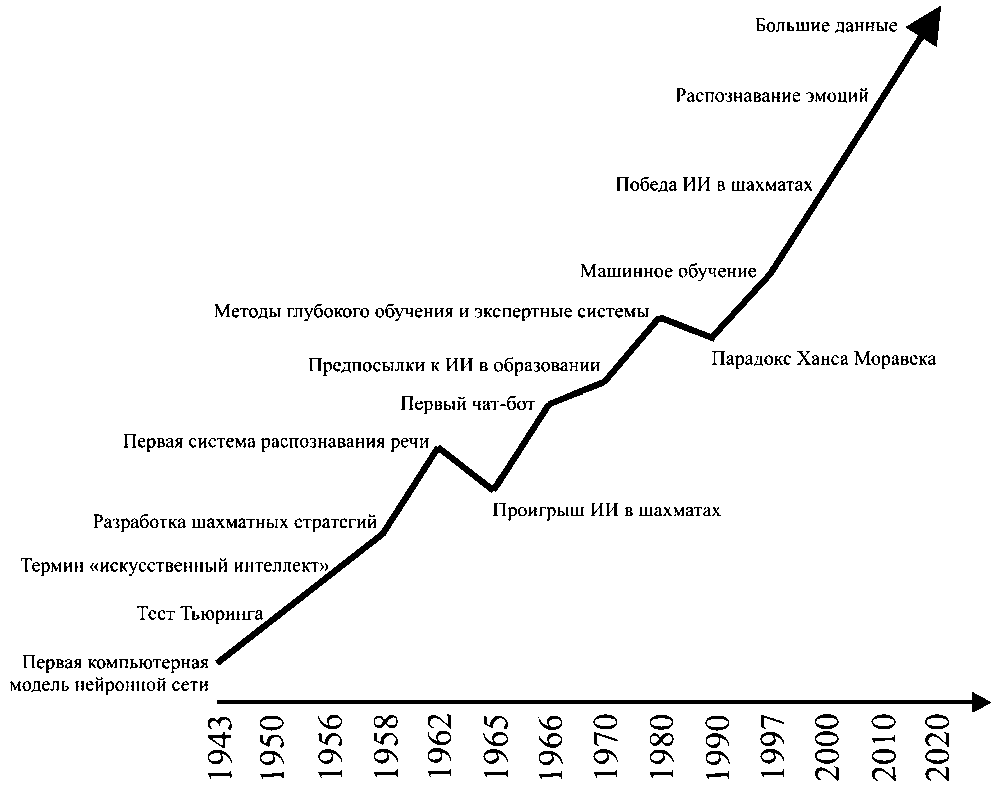
[Юрченков, Курганов, 2022]. Основываясь на данных работах, рассмотрим хронологию истории становления ИИ как направления в науке (рис. 2).

Большие данные

Распознавание эмоций

Победа ИИ в шахматах

Машинное обучение

Методы глубокого обучения и экспертные системы

Парадокс Ханса Моравека

Предпосылки к ИИ в образовании

Первый чат-бот

Первая система распознавания речи

Тест Тьюринга

Разработка шахматных стратегий

Термин «искусственный интеллекту

Проигрыш ИИ в шахматах

Первая компьютерная модель нейронной сети сп О О ОСО) Ш О О О О О ТГ Ш Ш UH O О О ОС ООО оо оооооооооо

Рис. 2. Хронологическая линейка развития искусственного интеллекта

Fig. 2. Chronological timeline of Artificial Intelligence development

1943 г. – Н. Винер, У. Питтс и У. Мак-Каллок теоретически обосновывают возможности создания ИИ на основе биологических нейронных сетей.

1950-е гг. – А. Тьюринг публикует ряд работ о том, может ли мыслить машина, предлагает идею эмпирического теста (тест Тьюринга: исследователь взаимодействует с одним компьютером и одним человеком. Исходя из полученных ответов на заданные вопросы, ему необходимо решить, общается ли он с программным обеспечением или с человеком. Основная цель программы – запутать исследователя, чтобы он принял неверное решение. Все испытуемые не имеют возможности видеть друг друга. Если исследователь не может однозначно определить, кто из участников является человеком, значит, машина успешно прошла данный тест.).

1956 г. – в работах Д. Маккарти, М. Мински, Н. Рочестера и К. Шеннона появляется термин «искусственный интеллект». Представлена первая программа ИИ – Logic Theorist.

1958 г. – Г. Саймон предполагает, что ИИ в ближайшие десять лет может обыграть чемпионов мира по шахматам.

1962 г. – IBM демонстрирует систему распознавания речи Shoebox (16 слов – цифры и команды для арифметических операций сложения и вычитания чисел).

1965 г. – ИИ проигрывает матч в соревнованиях по шахматам участникам возраста 10 лет.

1966 г. – создан первый GPT-чат «Элиза», который ведет беседу на естественном языке.

1970-е гг. – Дж. Карбонеллом создана программа SCHOLAR – интеллектуальная обучающая система.

о

о

S

о

и ы т S U о

W с

1980-е гг. – Д. Хопфилд и Д. Румельхарт представили методы «глубокого обучения», позволяющие компьютерам учиться на основе опыта. Э. Фейгенбаум представил системы, имитирующие принятие решений человеком.

1990-е гг. – Х. Моравек сформулировал парадокс: «достигнуть уровня взрослого в таких активностях, как тестирование на IQ или игра в шашки, достаточно просто. Однако освоить навыки, характерные для младенца, в области восприятия или познавательной активности либо сложно, либо вовсе невозможно».

1997 г. – разработаны алгоритмы Machine Learning, по которым компьютеры могут накапливать знания и обучаться на основе собственного опыта. Суперкомпьютер DEEP BLUE побеждает мировых чемпионов по шахматам.

2010-е гг. – появляется новое направление в исследованиях ИИ – аффективные, или эмоциональные, вычисления (англ. affective computing), анализирующие реакции и их воспроизведение.

2020-е гг. – появляются алгоритмы обработки Больших данных (англ. Big Data), методы глубокого обучения нейронных сетей [Юрченков, Курганов, 2022].

Рассмотрим алгоритм обработки текстовой информации на основе GPT-3-чата, размещенного для бесплатного использования в интернете . GPT-чат при обработке текста опирается на те данные, которые уже размещены в интернете, оперируя при этом более чем 175 миллиардами параметров. Например, при обращении к ИИ с просьбой дополнить фразу «методика обучения математике – это…» GPT-чат создаст список из возможных слов, просчитывая вероятность их присутствия в данном месте. Можно предположить, что следующим словом во фразе будет то, которое имеет самую высокую вероятность, однако создатели ИИ высказывают другое мнение: «… по какой-то причине (возможно, однажды мы ее узнаем), если всегда будет выбираться слово с самым высоким рейтингом, т.е. для которого определена самая высокая вероятность, мы получим очень гладкий текст, без малейшего признака креативности, который будет слово в слово повторять множество других текстов» [Вольфра, 2024, с. 17]. Нейросеть выбирает нужное слово для продолжения фразы случайным образом из всех возможных, имеющих вероятность примерно 0,8, при этом имея достаточно большой объем текста на русском языке, ИИ может определить вероятность выбора подходящих букв, слов, словосочетаний, предложений, фрагментов текста и т.д. На первый взгляд, технология достаточно простая, однако в интернете содержится несколько миллиардов слов, в книгах, которые были оцифрованы, еще 100 миллиардов. Но при наличии 200 тысяч общеупотребительных слов в русском языке (данные Национального корпуса русского языка) число возможных словосочетаний из двух слов составляет примерно 32 миллиарда, а число возможных комбинаций из трех слов – 160 триллионов и т.д. Для разрешения этой проблемы была разработана Большая языковая модель (англ. Large Language Model – LLM), она специально сконструирована для оценки вероятностей выбора слов и лежит в основе работы GPT-чатов.

Анализ графических данных происходит схожим образом: целое изображение распределяется на слои, происходит анализ отдельных объектов на каждом из слоев, высчитывается вероятность правильной интерпретации, корректности преобразования рисунка в векторную графику и последующей обработки.

По такому алгоритму работает, например, мобильный апплет Photomath (табл. 1). Приложение, получив изображение от камеры смартфона, разбивает его на отдельные части (цифры, буквенные символы, арифметические действия и т.д.), преобразует его в цифровой вид, понятный для программных средств вычисления, проводит математические действия и представляет последовательность вычислений, выдает ответ. Пример такой последовательности шагов, выполняемых приложением при решении дробно-рационального уравнения

9x2-4 5-Юх

, представлен в табл. 2.

x-1 1-х

Таблица 2

Последовательность некоторых действий мобильного апплета Photomath при решении дробно-рационального уравнения

Table 2

Sequence of actions of the Photomath mobile applet when solving a fractional rational equation

№ шага	Скриншот	№ шага	Скриншот
1	2	3	4
1		2	Сканирование и преобразование изображения в цифровой формат
3	9x2-4 5-10x x-1    1-x Найдите все значения x. при которых знаменатель дроби 9х2- 4 ---— равен 0 V х-1 = 0	…8	X = 1 Чтобы найти область допустимых значений, нужно удалить недопустимые значения V 2 9х - 4 5-Юх , -------------=-------------, X ?! 1 х-1    1-х
9	2 9х -4  5-10х ---------=-------- X X 1 х-1    1-х Упростите уравнение путем перекрестного умножения (эх2 - 4)x(l- x) = (5-10x)x(x-l)	…18	19х7-9х3 + 1-11х = 0 Использовать переместительный закон, чтобы изменить порядок членов V 3       2 -9х +19х -11х + 1=0
19	-9х3+ 19х -11х + 1 = 0 2 Запишите 19х в виде суммы V 3     2       2 -9х + 9х +10х -11х + 1 = 0	…23	-9х3 + 9х2 + 10х2-10х-х + 1 = 0 Вынести знак минус за скобки V -9x2x(x-l)+l0xx(x-l)-(x-l) = 0
24	—9хх(х — l)*10xx(x — 1)—(х —1) = 0 Вынести за скобки общий множитель -(х-1) V -(x-l)x(9x?-10x + l)=0	...30	-(x-l)Zx(9x-l) = 0 Изменить знаки обеих частей уравнения V (x-l)2x(9x-l) = 0

Окончание табл. 2

1	2	3	4
31	(x-l)2x(9x-l) = 0 Если произведение равно 0, то как минимум один из множителей равен 0 (х-1)’=0 9х-1=0	…34	X = I 1 х =—, х х1 9 Проверить, принадлежит ли решение заданному интервалу 1 х = — 9

Безусловно, представленный в табл. 2 алго-

ритм решения уравнения

9?-4_5-10x x-1     1-х

(состоящий из 34 шагов!!!), выполненный при помощи Photomath, не является рациональным, недоступен для понимания подавляющему большинству учащихся учреждений общего среднего образования. Платная версия мобильного апплета «Maple Калькулятор: решатель» проводит вычисления этого же уравнения за 12 шагов, однако предлагаемое подробное решение также сильно отличается от того алгоритма решения дробно-рациональных уравнений и его оформления, которое предлагается учащимся на уроках по математике11:

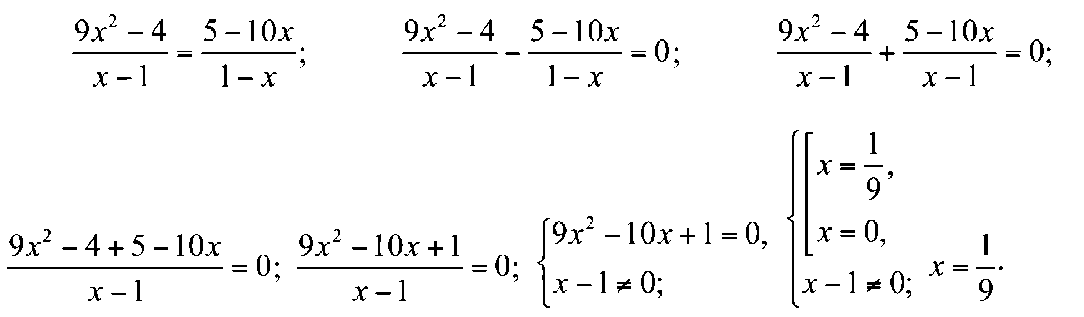
Очевидно, что такое решение значительно более рационально в сравнении с выполняемыми мобильными апплетами. Однако последние версии GPT-4-чатов (выпущенные в 2024 г., но работающие пока только в тестовом режиме) уже способны предлагать решения математических задач (алгебраические, из математического анализа и теории вероятностей и т.д.) и их оформления, неотличимые от проводимых человеком.

Нами разработан веб-ориентированный ресурс (далее – авторский ресурс) для сопровождения обучения учителей математики на повышении квалификации по теме «Дидактический дизайн в преподавании математики в учреждениях общего среднего образования»12. Разработка учебной программы ПКиСД была обусловлена необходимостью комплексной модернизации образовательного процесса посредством использования цифровых инструментов, формирования у учителей математики навыков работы со специальными онлайн-сервисами и приложениями по созданию дидактических многомерных инструментов и информационно емких визуальных материалов. Учебная программа ПКиСД учителей математики направлена на совершенствование их профессиональной компетентности в области структурирования и визуализации учебной информации с использованием современных компьютерных приложений. В ходе обучения слушатели осваивают технологии построения дидактических многомерных инструментов, а также методику их использования на учебных занятиях. Авторский ресурс рекомендован к использованию в процессе ПКиСД учителей математики Научно-методическим советом государственного учреждения образования «Минский городской институт развития образования» (протокол от 27.01.2025 № 1) и включает:

– глоссарий (более 180 понятий и терминов);

– следующие формы установления взаимодействия, учебной и профессиональной коммуникации преподавателя со слушателями (учителями математики): форум «Вопрос-ответ» (обсуждение заданий, методическая поддержка, техническая поддержка), чат-бот «Профессор МГИРО» (@professorMGIRO_bot) – телеграм-чат на основе ИИ;

– материалы для освоения содержания программы ПКиСД учителями математики «Дидактический дизайн в преподавании математики в учреждениях общего среднего образования»: вопросы государственной политики в сфере цифровизации образования (2 темы), научнотеоретические основания структурирования содержания обучения математике (5 тем), основы работы со специализированным программным обеспечением (11 тем);

– примеры фрагментов дидактических сценариев учебных занятий, отражающих методику использования дидактических многомерных инструментов при обучении математике (база постоянно пополняется материалами, разработанными учителями математики в процессе ПКиСД);

– коллекцию готовых учебных математических апплетов и методические указания по их использованию на учебных занятиях по математике на II–III ступенях общего среднего образования;

– фрагменты видео лекций и практических занятий, где даются инструкции по работе с компьютерными программными средствами: редакторами векторной графики, динамическими программными средами, конструкторами инфографики, учебными математическими апплетами, GPT-чатами и т.д., а также алгоритмы разработки собственных веб-ориентированных ресурсов;

– материалы для текущей и итоговой аттестации (дифференцированные по трем уровням сложности).

Каждая учебная тема, размещенная на авторском ресурсе, состоит из основного материала, дополнительной литературы, заданий для самостоятельного выполнения. Содержательный блок авторского ресурса, обеспечивающего повышение ПКиСД учителей математики, имеет спиралевидную конструкцию из четырех витков :

• 1)    учителя математики под руководством преподавателя осваивают алгоритмы структурирования учебной информации для учащихся II–III ступеней общего среднего образования с использованием возможностей дидактического дизайна (таблицы, блок-схемы и т.д.) и простых веб-ориентированных ресурсов (веб-презентации, онлайн-интерактивные доски и т.д.). Например: «Используя возможности Google Disk, создайте электронную таблицу «Свойства тригонометрической функции fx ) = sin x » (область определения/ значения, четность/нечетность, периодичность, промежутки возрастания/убывания, достижение максимального/минимального значения, интервалы положительных/отрицательных значений, нули функций);

• 2)    учебная информация предыдущего витка обогащена алгоритмами решения педагогических задач на основе использования различных существующих веб-ориентированных ресурсов, применения на учебных занятиях по математике информационно емких визуальных изображений (учебные математические апплеты, инфографика, структурно-логические схемы и т.д.) по отдельным учебным темам в готовом виде. Например: «Используя созданную ранее электронную таблицу и возможности онлайн-редактора

  
  

, создайте инфографику по теме «Свойства тригонометрической функции fx) = sin x». Дополните созданную инфографику ссылками на учебные математические апплеты библиотеки сайта »;

• 3)    содержание обучения дает возмож-

• ность учителям математики под руководством преподавателя самостоятельно разрабатывать веб-ориентированные ресурсы, рассматривать различные методические аспекты обучения учащихся навыкам обобщения и структурирования учебной информации по укрупненным темам (логико-смысловые модели, учебные математические апплеты и т.д.), прогнозировать свою

педагогическую деятельность в конкретном классе на перспективу. Например: «Используя возможности динамического программного онлайн-сервиса 1С: “Математический конструктор” создайте учебный математический апплет “Тригонометрическая функция (синус)”, в котором отображается график тригонометрической функции вида flx) = a\bn(bx + с) + d, где a, b, d – параметры со значениями от –5 до 5, шаг из-71

менения 0,1, с – параметр со значением от

Л             Л                2

до , шаг изменения . Настройте апплет так, 2               12

чтобы в записи тригонометрической функции отображались значения параметров (коэффициентов) a, b, с, d. Например:

.»;

• 4)    предназначен преимущественно для самостоятельного освоения учителями математики способов построения процесса обучения математике с использованием веб-

• ориентированных ресурсов, что позволяет слушателям самостоятельно обобщить и транслировать свой педагогический опыт коллегам. Например: «Дополните учебный математический апплет еще одним параметром вида х = e, где е - параметр со значениями от –5 до 5, шаг изменения 0,1. Оформите апплет так, чтобы с его помощью можно было визуализировать решение тригонометрического уравнения вида , где a, b, d, e – действительные числа от –5 до 5, шаг

изменения 0,1, с – параметр со значением от

л               л                  2

до , шаг изменения . Разработайте сцена-

рий проведения учебного занятия с использо- ванием данных апплетов. Перешлите коллегам для экспертизы разработанный вами апплет и сценарий учебного занятия».

Каждый виток спирали включает в себя несколько слоев: содержательный слой, который представляет собой теоретическое обоб- щение укрупненных дидактических единиц математического, дидактического и методического знания; информационно-технический слой, содержащий инструкции и алгоритмы работы с доступными ресурсами, а также рекомендации по самостоятельной разработке веб-ориентированных ресурсов, и методический слой, который охватывает методику и технологии использования веб-ориентированных ресурсов на учебных занятиях по математике.

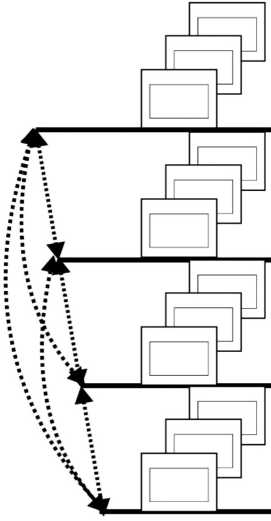
Структурно-логическая схема освоения содержания обучения при ПКиСД учителей математики, представлена на рис. 3.

Телеграм-бот «Профессор МГИРО» разработан на основе технологии нейросетей GPT-4, свободно ведет диалог по содержанию учебной программы повышения квалификации учителей математики по теме «Дидактический дизайн в преподавании математики в учреждениях общего среднего образования». Кроме общедоступных баз методической литературы и цифровых образовательных технологий, в телеграм-бот добавлены дополнительные векторные базы: 12 пособий по методике преподавания математики и внешние базы данных, касающиеся применения ИКТ в образовательном процессе.

В целях безопасности и противодействия нарушению нормативных правовых положений, распространению фейков и деструктивной информации, а также с целью соблюдения морально-этических норм педагога алгоритм ИИ телеграм-бота «Профессор МГИРО» жестко ограничен рамками содержания методики обучения математике, психолого-педагогическими требованиями к разработке и внедрению цифровых технологий в образовательный процесс.

4-й виток - обобщение, транслирование своего педагогического опыта по разработке и использованию веб-ориентированных ресурсов, дидактического дизайна

3-й виток - разработка веб-ориентированных ресурсов, обобщение и структурирование учебной информации по укрупненным темам (логико-смысловые модели, учебные математические апплеты и т.д.), прогнозирование педагогической деяте льности в конкретном классе на несколько лет вперед 2-й виток - использование существующих веб-ориентированных ресурсов, информационно емких визуальных изображений (учебные математические апплеты, инфографика, структурно-логические схемы и т.д.) по отдел ьным учебным темам в готовом виде

1-й виток - структурирование и представление учебной информации в графическом виде (таблицы, блок-схемы и т.д.) с использованием презентации и/или интерактивной доски

3 пласта фундирования:

- Содержательный пласт

- Информационно-технический пласт

- Методический пласт

- Свободный переход между витками

Рис. 3. Структурно-логическая схема освоения содержания обучения учителями математики на веб-ориентированном ресурсе

Fig. 3. Structural and logical diagram of mastering the content of teaching by mathematics teachers on a web-oriented resource

В случае если пользователь попытается задать вопрос, выходящий за рамки ограничений, телеграм-бот выдаст ответ: «Извините, но я не могу обсуждать вопросы, не связанные с методикой обучения математике и цифровыми технологиями. Если у Вас есть вопросы по дидактическому дизайну, преподаванию математики или внедрению цифровых технологий в образовательный процесс, я с радостью помогу Вам!».

Заключение. Искусственный интеллект все прочнее входит во все социально-экономические аспекты жизни человека, в том числе определяет вектор развития цифровизации процессов системы образования. На данный момент еще не в полной мере разрешены психолого-педагогические и морально-этические проблемы, связанные с взаимодействием педагогических работников и особенно учащихся учреждений общего среднего образования с нейронными сетями. В статье представлено авторское видение возможного разрешения несоответствия между запросом общества в обогащении методического инструментария учителей математики веб-ориентированными ресурсами обучения, включающими современные возможности нейросетей, ИИ, GPT-чатов и мобильных учебных математических апплетов, и недостаточной разработанностью методологического, методического, технологического и технического аспектов данного процесса. Считаем перспективным внедрение разработанной дидактической системы ПКиСД учителей математики, направленной на повышение их уровня профессиональных компетенций, в том числе в области цифровых технологий, в систему дополнительного педагогического образования.