Применение высокопроизводительных вычислений для поиска троек взаимно частично ортогональных диагональных латинских квадратов порядка 10

Латинский квадрат порядка n – это квадратная таблица размеров n × n, заполненная элементами некоторого множества M, |M| = n таким образом, что в каждой строке и в каждом столбце таблицы каждый элемент из M встречается в точности один раз [1]. В дальнейшем в настоящей статье в качестве M будет использовано множество {0,…, n -1}. Латинские квадраты и системы, построенные на их основе, применяются в многих прикладных областях: теории кодирования (см., например, [2]), криптографии (см. [3]) и т.д. Диагональный латинский квадрат порядка n – это латинский квадрат, в котором каждый элемент из M, |M| = n встречается в точности один раз не только в каждой строке и каждом столбце, но и в главной и побочной диагоналях.

Пара латинских квадратов одинакового порядка называется ортогональной, если различны все упорядоченные пары элементов (a, b), где a - элемент в некоторой ячейке первого латинского квадрата, а b - элемент в ячейке с тем же номером второго латинского квадрата. Другими словами, два латинские квадрата порядка n ортогональны, если при наложении одного квадрата на другой образуется новый квадрат, в котором все n2 элементов будут различны (такой квадрат называется греко-латинским). Если имеется набор из m различных латинских квадратов, любая пара которых ортогональна, то говорят о системе из m взаимно ортогональных латинских квадратов. Пара латинских квадратов порядка n называется частично ортогональной, если условие ортогональности между ними может выполняться не полностью, т.е. если при наложении одного латинского квадрата на другой среди n2 элементов получаемого квадрата могут быть повторяющиеся элементы.

Диагональные латинские квадраты порядка 10 пока относительно слабо изучены, то же самое можно сказать и про ортогональные системы, построенные на их основе. Если первая пара ортогональных латинских квадратов порядка 10 была найдена еще в 1959 г. (см. [1]), то первая пара ортогональных диагональных латинских квадратов порядка 10 была найдена только в 1992 г. [4]. Более конкретно, в статье [4] были представлены три такие пары. Количество диагональных латинских квадратов порядка 10 до сих пор неизвестно, при этом количество латинских квадратов порядка 10 было установлено в 1995 г. (см. [1]).

Одной из самых известных открытых задач комбинаторики является следующая: определить, существует ли тройка взаимно ортогональных латинских квадратов порядка 10. Эта задача чрезвычайно сложна, поэтому в последнее время интенсивно развиваются алгоритмы поиска троек взаимно частично ортогональных латинских квадратов порядка 10. В статье [5] приведен текущий рекорд в этом направлении - тройка A, B, C латинских квадратов порядка 10, в которой A ортогонален B и C, а B и C образуют частично ортогональную пару с 91 различными упорядоченными парами элементов из 100 возможных. Под рекордом здесь понимается то, что данная тройка является наиболее близкой к тройке попарно ортогональных латинских квадратов порядка 10 (из опубликованных в открытой печати).

Данная статья посвящена поиску новых троек взаимно частично ортогональных диагональных латинских квадратов порядка 10. Для этого используется подход, согласно которому осуществляется поиск пар ортогональных диагональных латинских квадратов порядка 10, а затем для каждой такой пары достраивается третий диагональный латинский квадрат таким образом, чтобы получаемая тройка удовлетворяла заданным характеристикам. Большая часть экспериментов была проведена в рамках проекта добровольных распределенных вычислений SAT@home и на вычислительном кластере.

Статья имеет следующую структуру. Во втором разделе описаны новые результаты применения SAT-подхода к поиску систем диагональных латинских квадратов порядка 10. Описан эксперимент, в результате которого в проекте добровольных распределенных вычислений SAT@home были найдены новые пары ортогональных диагональных латинских квадратов порядка 10. Приведены результаты поиска троек взаимно частично ортогональных диагональных латинских квадратов порядка 10. Завершает второй раздел доказательство того факта, что на основе всех известных в настоящее время пар ортогональных диагональных латинских квадратов порядка 10 невозможно построить трой- ку взаимно ортогональных диагональных латинских квадратов порядка 10. В третьем разделе описаны два переборных алгоритма построения диагональных латинских квадратов порядка 10, а также результаты применения этих алгоритмов к поиску троек взаимно частично ортогональных диагональных латинских квадратов порядка 10.

• 1.    Поиск систем диагональных латинских квадратов порядка 10 как задача о булевой выполнимости

Задачи поиска комбинаторных структур можно решать с помощью различных подходов. В данном разделе развивается SAT-подход к решению таких задач, состоящий в сведении исходной задачи к проблеме булевой выполнимости (SAT) [6]. Для использования SAT-подхода необходимо перейти от исходной постановки к булевому уравнению вида «КНФ=1» (здесь КНФ – это конъюнктивная нормальная форма). Такой переход называется пропозициональным кодированием исходной задачи. Все известные алгоритмы решения SAT-задач экспоненциальны в худшем случае, т.к. SAT является NP-трудной задачей (NP-полной в распознавательном варианте). Несмотря на это, современные SAT-решатели (в том числе параллельные и распределенные) успешно справляются с решением многих трудных SAT-задач, кодирующих задачи из различных предметных областей. Большинство из современных SAT-решателей основано на алгоритме Conflict-Driven Clause Learning (CDCL). Базовые принципы этого алгоритма, а также ряд эвристик и структур данных, используемых для его ускорения, рассмотрены в обзорной статье [7]. Применение SAT-подхода к поиску различных систем ортогональных латинских квадратов описано в обзорной статье [8].

• 1.1.    Поиск пар диагональных латинских квадратов порядка 10 как задача о булевой выполнимости

  В 2012 г. в проекте добровольных распределенных вычислений SAT@home [9], построенном на платформе BOINC [10], был запущен эксперимент, направленный на поиск новых пар ортогональных диагональных латинских квадратов порядка 10. Результаты этого эксперимента описаны в [11]. Сначала была сделана пропозициональная кодировка указанной задачи. Полученная в результате КНФ состоит из 2000 переменных и 434440 дизъюнктов, файл с КНФ в формате DIMACS занимает около 10 мегабайт. Применялась т.н. «наивная» схема кодирования, при которой каждой ячейке каждого искомого квадрата сопоставляются 10 булевых переменных КНФ. Распараллеливание полученной SAT-задачи на подзадачи проводилось следующим образом. Первая строка первого диагонального латинского квадрата фиксировалось в значении «0 1 2 3 4 5 6 7 8 9», а значения первых 8 ячеек второй и третьей строки варьировались (т.е. перебирались все возможные их значения). Упомянутое фиксирование значения первой строки возможно потому, что любой латинский квадрат можно эффективно привести к такому виду. В итоге в каждой получаемой подзадаче в первом диагональном латинском квадрате из искомой пары были известны значения 26 из 100 ячеек (10 из первой строки и по 8 из второй и третьей строки), это обеспечивалось подстановкой значений 260 из 2000 переменных КНФ. В качестве задания проекта SAT@home выдавался пакет из 20 таких подзадач. На каждую подзадачу из пакета был установлен лимит в 2600 рестартов SAT-решателя Minisat [12] (модифицированный вариант этого решателя используется в качестве расчетного приложения в SAT@home), что примерно соответствует 4 минутам ра-

  боты одного ядра современного процессора. На обработку 20 миллионов подзадач, сгенерированных для данного эксперимента, потребовалось около 9 месяцев работы SAT@home (с сентября 2012 года по май 2013 года). В результате были найдены 17 новых пар ортогональных диагональных латинских квадратов порядка 10 (в дополнение к трем ранее известным парам квадратов из статьи [4]).

В апреле 2015 г. в проекте SAT@home нами был запущен эксперимент, направленный на поиск новых пар ортогональных диагональных латинских квадратов порядка 10. Отметим, что разбиение исходной задачи на подзадачи, использованное в 2012-2013 гг. (см. [11]), было выбрано из разумных соображений. В этот раз было принято решение подойти к выбору типа разбиения более систематично. В табл. 1 указаны 8 разбиений и результаты, полученные с их помощью. Всего с 17 апреля 2015 г. по 12 февраля 2016 г. были найдены 32 новые пары ортогональных диагональных латинских квадратов порядка 10 (мы сравнивали их с 3 парами из статьи [4] и 17 парами из статьи [11]), все они выложены в разделе «Найденные решения» проекта SAT@home. При этом было использовано то же расчетное приложение с тем же лимитом на количество рестартов, что и в 2012 г. Во всех разбиениях использовались первые ячейки в строках (т.к. первая строка всегда фиксируется, строки брались начиная со второй).

Таблица 1

Результаты применения различных разбиений для поиска пар ортогональных диагональных латинских квадратов порядка 10 в проекте SAT@home

Вид разбиения	Найдено пар	Дата	Статус
1 строка, 9 ячеек	1	1 месяц в 2015 г.	Завершен
2 строки по 2 ячейки	–	1 день в 2015 г.	Завершен
2 строки по 3 ячейки	–	3 дня в 2015 г.	Завершен
2 строки по 4 ячейки	–	2 недели в 2015 г.	Завершен
2 строки по 5 ячеек	26	6 месяцев в 2015-2016 гг.	В процессе
2 строки по 6 ячеек	5	2 месяца в 2015 г.	Приостановлен
2 строки по 7 ячеек	–	–	Не запущен
2 строки по 8 ячеек	17	9 месяцев в 2012-2013 гг.	Приостановлен

Проанализируем табл. 1. Разбиение «2 строки по 8 ячеек» соответствует разбиению из [11], разбиение «2 строки по 7 ячеек» еще не запускалось, а остальные 6 разбиений были запущены в 2015 г. С помощью разбиений «2 строки по 2 ячейки», «2 строки по 3 ячейки» и «2 строки по 4 ячейки» не было найдено ни одной новой пары. Разбиение «2 строки по 5 ячеек» оказалось более эффективно, чем использованное в [11] разбиение «2 строки по 8 ячеек», т.к. обеспечило нахождение большего количества искомых пар за

Применение высокопроизводительных вычислений для поиска троек взаимно... единицу времени (даже с учетом того, что в 2015-2016 гг. производительность SAT@home примерно в два раза выше, чем в 2012-2013 гг.).

• 1.2.    Поиск троек взаимно частично ортогональных диагональных латинских квадратов порядка 10 как задача о булевой выполнимости

• 2.    Применение метода грубой силы для построения диагональных латинских квадратов порядка 10

Рассмотрим тройку диагональных латинских квадратов одного и того же порядка. Характеристикой частично ортогональной тройки далее называется множество различных упорядоченных пар элементов, по которым выполняется условие ортогональности для каждой из трех пар квадратов из тройки.

В статье [11] был описан алгоритм построения троек взаимно частично ортогональных диагональных латинских квадратов порядка 10. Согласно этому алгоритму запускается генерация диагональных латинских квадратов порядка 10, и на основе каждого сгенерированного квадрата строятся частично ортогональные тройки с задействованием каждой из известных ортогональных пар (на основе каждой известной пары строится отдельная тройка). В результате применения этого алгоритма была найдена частично ортогональная тройка с характеристикой 62, тогда как в статье [4] приведена частично ортогональная тройка с характеристикой 60.

В статье [13] предлагается рассматривать задачу построения таких троек как задачу о булевой выполнимости. Конкретнее, была предложена пропозициональная кодировка поиска таких троек, в которой редактированием специального дизъюнкта можно задавать требуемое значение характеристики ортогональности. Если в полученную КНФ подставить значения двух квадратов из некоторой известной пары, то задача сводится к поиску диагонального латинского квадрата, который с подставленной парой квадратов образует частично ортогональную тройку с заданной характеристикой. С помощью данного подхода была найдена тройка взаимно частично ортогональных диагональных латинских квадратов порядка 10 с характеристикой 73 [13]. Для этого был использован многопоточный SAT-решатель treengeling [14], который запускался на одном узле вычислительного кластера и задействовал на нем 32 процессорных ядра. Для каждой известной пары ортогональных диагональных латинских квадратов (на тот момент таковых было 20) строилась отдельная КНФ, подставляя значения двух известных квадратов в описанную выше кодировку.

Т.к. в 2015-2016 гг. в SAT@home были найдены еще 32 пары ортогональных диагональных латинских квадратов порядка 10 (см. раздел 2.1), то на их основе было сделано еще 32 КНФ в дополнение к 20, рассмотренным в [13]. В результате запуска на них SAT-решателя treengeling были найдены еще две частично ортогональные тройки с характеристикой 73. Они были построены на основе 4-й и 15-й пар, найденных в рамках эксперимента, описанного в разделе 2.1. Соответствующие пары в разделе «Найденные решения» сайта проекта SAT@home отмечены как найденные 25 июня и 23 августа 2015 г. Обе найденные тройки выложены на сайте SAT@home в разделе «Ортогональные и частично ортогональные системы латинских квадратов порядка 10».

Предложенная в [13] пропозициональная кодировка позволила получить еще одно семейство результатов. С помощью данной кодировки можно установить требование, чтобы характеристика частично ортогональной тройки порядка 10 была равна 100, т.е. фактически тем самым потребовать нахождение тройки попарно ортогональных диаго- нальных латинских квадратов порядка 10 без каких-либо ослаблений. При этом подстановка в соответствующую КНФ значений квадратов из известной пары ставит задачу следующим образом: для заданной пары ортогональных диагональных латинских квадратов порядка 10 найти третий диагональный латинский квадрат, образующий с первыми двумя квадратами взаимно ортогональную тройку, либо констатировать факт отсутствия такого диагонального латинского квадрата. Были построены 52 КНФ с подстановкой в каждую из них значений квадратов из соответствующих пар (3 пары из [4], 17 из [11], а еще 32 были найдены в рамках данного исследования, см. раздел 2.1). В каждую из этих КНФ было внесено требование «значение характеристики равно 100». SAT-задачи для всех этих КНФ были решены SAT-решателем plingeling [14] в среднем примерно за одну секунду на 32 процессорных ядрах (были использованы 2 16-ядерных процессора AMD Opteron 6276), и все ответы были «UNSAT». Это означает, что решатель plingeling сделал вывод о невыполнимости всех этих КНФ. Напомним, что КНФ является невыполнимой, если отсутствует такой набор значений переменных из этой КНФ, который бы обращал ее в 1. Отметим, что в [15] была формально доказана корректность алгоритма DPLL (Davis–Putnam–Logemann–Loveland) – т.е. было доказано, что если алгоритму DPLL удается найти решение SAT-задачи, то это решение является правильным. В том числе это касается и случая, когда алгоритм DPLL делает заключение о невыполнимости данной на вход КНФ. В решателе plingeling, основанном на алгоритме DPLL, добавлен ряд усовершенствований (например, добавлена процедура CDCL), которые, тем не менее, не нарушают корректность базового алгоритма DPLL [14]. Из вышеупомянутых фактов следует, что все построенные КНФ оказались действительно невыполнимыми, т.к это было доказано используемым корректным алгоритмом. А из этого факта в свою очередь следует, что на основе всех 52 известных на данный момент пар ортогональных диагональных латинских квадратов порядка 10 невозможно построить тройку взаимно ортогональных диагональных латинских квадратов порядка 10. Дополнительно, на данный момент для всех 52 известных ортогональных пар описанным выше способом удалось провести доказательство невозможности построения взаимно частично ортогональных троек для случая «значение характеристики равно 87». Эти задачи оказались уже довольно сложными – решателю plingeling понадобилось в среднем 8 часов работы для каждой такой КНФ, при этом он работал на 32 ядрах.

В статье [11] для построения троек взаимно частично ортогональных диагональных латинских квадратов порядка 10 использовался алгоритм поиска с возвратом, предназначенный для генерации диагональных латинских квадратов порядка 10 (см. раздел 2.2). При этом заполнение происходит слева направо сверху вниз по ячейкам квадрата. Поиск завершается, если найден некоторый диагональный латинский квадрат. После подстановки каждого нового значения в некоторую ячейку осуществляется проверка, нарушает ли текущее заполнение таблицы условия, накладываемые на элементы в диагональном латинском квадрате. Если заполнение не прошло проверку, происходит возврат до ближайшей ячейки, элемент которой нарушает условия, после чего этой ячейке назначается другое допустимое значение. История неудачных использованных значений хранится для каждой ячейки квадрата. Это нужно для того, чтобы исключить повтор вариантов, которые приводят к недопустимым заполнениям. Если для некоторой ячейки требуется поменять значение, но исчерпано множество допустимых вариантов, то происходит возврат на предыдущую ячейку. Реализация данного алгоритма позволила получать примерно по одному диагональному латинскому квадрату в секунду на одном ядре процессора.

Далее описываются два переборных алгоритма генерации диагональных латинских квадратов порядка 10. Они были разработаны и реализованы, во-первых, для того, чтобы сравнить их по скорости генерации с упомянутым выше алгоритмом поиска с возвратом. Во-вторых, с помощью данных алгоритмов планировалось найти новые тройки частично ортогональных диагональных латинских квадратов.

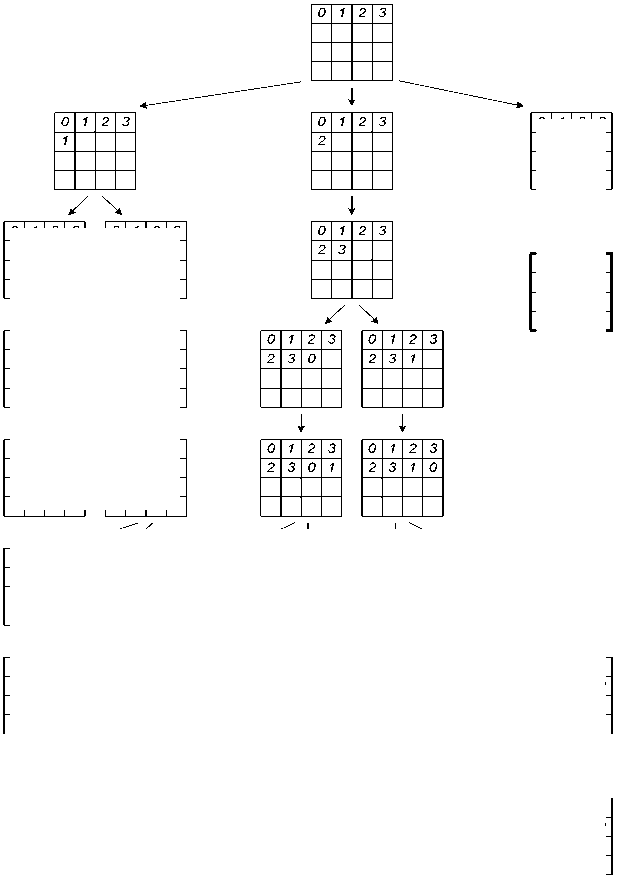
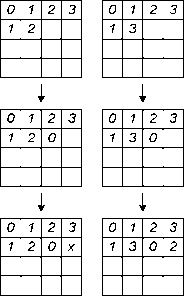
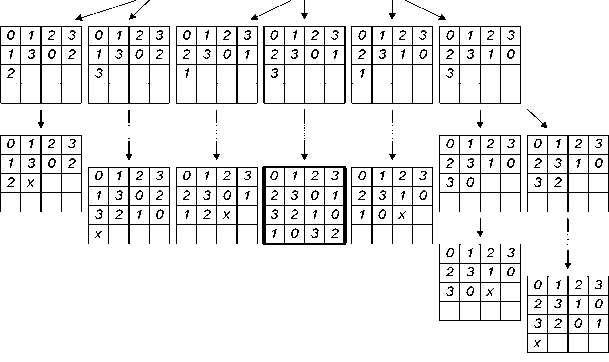
Рис. 1. Пример формирования диагонального латинского квадрата 4-го порядка: крестами отмечены элементы, для которых S jj = 0; жирным выделены найденные решения

Опишем первый переборный алгоритм. Простейшим способом реализации метода грубой силы является последовательное заполнение элементов формируемой структуры данных (например, латинского квадрата), значениями в соответствии с известным порядком обхода формируемого комбинаторного дерева в глубину. При этом после осуществления комбинаторного спуска для каждого нового элемента формируемой структуры данных (в простейшем случае - элемента a^j латинского квадрата), следуя работе [16], производится построение множества Sjj допустимых элементов, которые не нарушают ограничений задачи (например, не встречались в -й строке и j-м столбце). Каждому элементу указанного множества соответствует поддерево в дереве комбинаторного перебора, для них поочередно производится комбинаторный спуск, и процесс заполнения элементов формируемой структуры данных рекуррентно продолжается. Если на каком-либо шаге доступных элементов нет (т.е. Sjj = 0), то производится рекуррентный возврат на один ярус дерева комбинаторного перебора вверх, что соответствует методу ветвей и границ [17] и приводит к снижению числа анализируемых узлов дерева и, соответственно, к снижению затрат машинного времени при программной реализации. Схематично процесс комбинаторного перебора при построении диагонального латинского квадрата порядка 4 изображен на рис. 1.

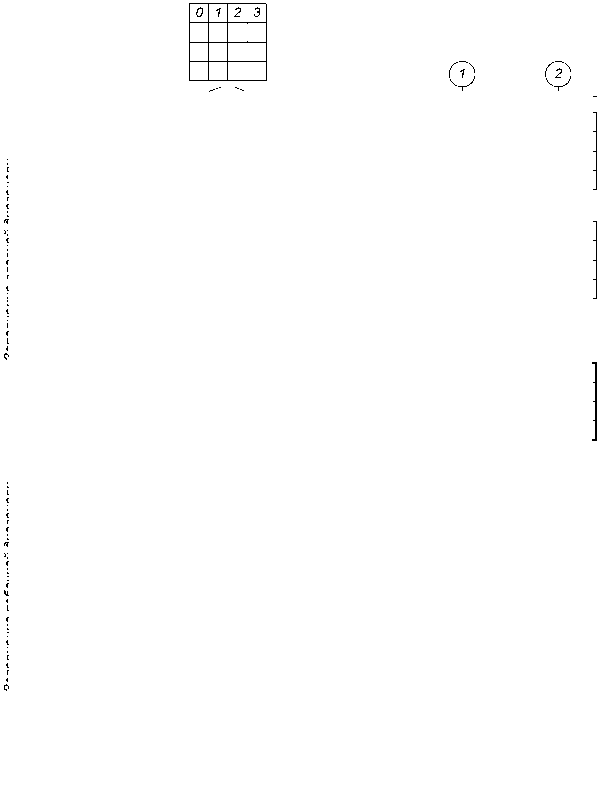
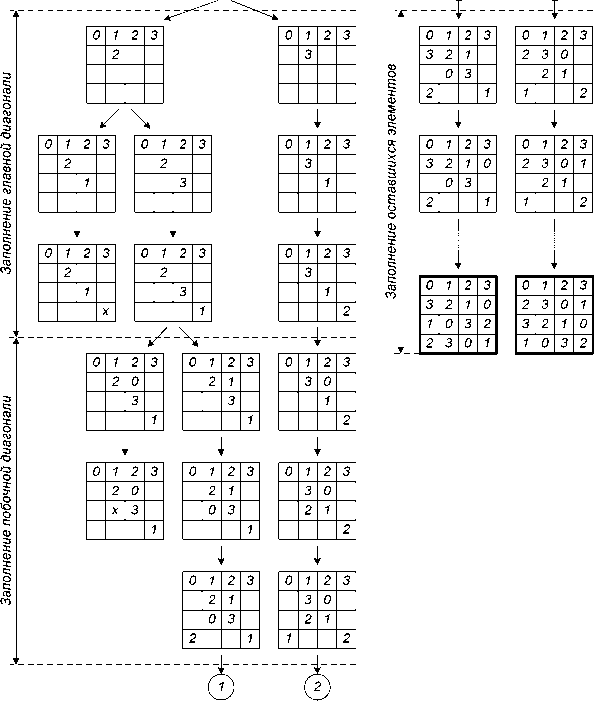
Рис. 2. Дерево комбинаторного перебора, соответствующее диагональному заполнению элементов (по сравнению с деревом, изображенным на рис. 1, число ветвей значительно меньше)

Несложно заметить, что некоторым поддеревьям не соответствует ни одного корректного решения (например, при построении нормализованного диагонального латинского квадрата 4 порядка с а21 = 1), однако данный факт устанавливается только после перебора всех узлов соответствующего поддерева, на что фактически впустую расходуется машинное время. При формировании диагональных латинских квадратов вероятность появления данной ситуации можно постараться снизить путем изменения порядка заполнения элементов формируемого квадрата (в работах [18, 19] показано, что изменение порядка рассмотрения элементов при формировании решения может оказывать существенное влияние на качество результирующего решения). Можно заметить, что максимальное число ограничений присутствует у элементов, расположенных на главной и побочной диагоналях квадрата (уникальность в строке, в столбце и на соответствующей диагонали), в то время как остальные элементы имеют меньшее число ограничений (уникальность в строке и в столбце). Исходя из данной особенности, заполнение элементов формируемого квадрата с использованием метода полного перебора можно производить в следующем порядке: сперва заполняются элементы главной диагонали, затем производится заполнение элементов побочной диагонали, а уже затем – всех остальных. При этом достигается более раннее возникновение возможных нарушений, что позволяет производить раннее отсечение неперспективных решений без анализа соответствующих поддеревьев (см. рис. 2).

Второй алгоритм построен на работе с т.н. версиями строк квадрата. Версия строки представляет собой номер перестановки её элементов. Например, для строки квадрата 4го порядка возможные перестановки приведены в табл. 2.

Таблица 2

Возможные перестановки из 4 элементов

№ версии	Вид строки
0	0 1 2 3
1	0 1 3 4
22	3 2 0 1
23	3 2 1 0

Перед работой алгоритма производится построение словаря, включающего в своем составе все возможные перестановки. Наличие подобного словаря не является обязательным, т.к. перестановки можно генерировать и на лету, однако их однократное создание и последующее многократное использование делает поиск быстрее.

В процессе поиска алгоритм оперирует двумя массивами – массивом с данными латинского квадрата и массивом с перечнем версий строк данного квадрата. Пример массива для диагонального латинского квадрата 6-го порядка приведен в табл. 3.

В соответствии с требованием нормализации построение квадрата начинается с первой строки, версии которой задается значение 0, после этого алгоритм производит рекуррентные спуски на следующие строки, подбирая их так, чтобы в уже сформированной части квадрата выполнялись условия несовпадения значений внутри столбцов и диагоналей. При этом уникальность элементов строки автоматически следует из определения перестановки.

Таблица 3

Пример кодирования диагонального латинского квадрата с использованием номеров версий (перестановок)

Версии строк	Квадрат
0	0 1 2 3 4 5
148	1 2 0 5 3 4
719	5 4 3 2 1 0
466	3 5 1 4 0 2
253	2 0 4 1 5 3
571	4 3 5 0 2 1

Описанные выше алгоритмы были реализованы в виде последовательной программы на языке C++. При этом первый из алгоритмов был реализован в двух вариантах очередности обхода ячеек квадрата, описанных выше. Тестирование этих алгоритмов проводилось на ПК с процессором AMD Phenom II X965. Тестирование проводилось в течении 1 часа. С помощью второго алгоритма (оперирующего со строками) не удалось найти ни одного диагонального латинского квадрата порядка 10. Первый алгоритм с вариантом очередности обхода ячеек подряд (слева направо сверху вниз) обеспечил генерацию 422 диагональных латинских квадратов в секунду, а во втором варианте (с первоочередным обходом ячеек главной и побочной диагоналей) – 5120 диагональных латинских квадратов в секунду. Отметим, что алгоритм поиска с возвратом из статьи [11] обеспечивал генерацию примерно 1 диагонального латинского квадрата в секунду на похожей конфигурации ПК.

01234 ⎡1 2 0 4 5 ⎢48 1 5 9

798 3 6⎤ 62073⎥

⎢8 3 46

⎢7 5 9 1

⎢3 6 5 2

⎢69 8 7

⎢94 78

⎣5 7 3 0

7 1 5 9 2 0⎥ 6 3 0 2 48⎥ 1 9 8 4 0 7⎥ 3 045 12⎥ 023 165⎥ 2 8 1 6 9 4⎦

0123456789 6831795402 2390874165 5706138294 7984521036 1278349650 8567012943 9452680371 3649207518 4015963827

0=

0123456789 7452103968 1034265897 2301894576 5867920314 6945781032 9680537241 4219078653 8576319420 3798642105

Рис. 3 . Тройка взаимно частично ортогональных диагональных латинских квадратов порядка 10 с характеристикой 66

На основе первого алгоритма была сделана MPI-программа на языке C++. Был использован вариант обхода ячеек подряд слева направо сверху вниз. В этой программе исходная задача разбивалась на семейство подзадач путем варьирования первых пяти ячеек второй и третьей строки квадрата (по аналогии с алгоритмом разбиения задачи из раздела 2.1). В рамках этой программы генерация диагональных латинских квадратов была использована для построения троек взаимно частично ортогональных диагональных латинских квадратов порядка 10 таким же образом, как было сделано в [11] (см. раздел 2.2). MPI-программа была запущена на 96 часов на 10 узлах вычислительного кластера «Академик В.М. Матросов» Иркутского суперкомпьютерного центра СО РАН. Каждый узел этого кластера включает в себя 2 16-ядерных процессора AMD Opteron

6276, т.е. суммарно программа работала на 320 ядрах. В результате была найдена частично ортогональная тройка с характеристикой 66 (см. рис. 3).

Отметим, что в [11] подобным подходом была найдена частично ортогональная тройка с характеристикой 62, при этом был задействован примерно такой же объем вычислительных ресурсов. Данный факт объясняется тем, что, как было упомянуто выше, предложенный переборный алгоритм даже в своем более медленном варианте обхода ячеек обеспечивает значительно более высокую скорость генерации, чем алгоритм поиска с возвратом.

Исходя из того, что в разделе 2.2 приведены частично ортогональные тройки с характеристикой 73, можно сделать вывод, что SAT-подход конкретно для этой задачи подходит лучше, чем переборные алгоритмы, предложенные в данном разделе (и тем более лучше, чем алгоритм поиска с возвратом). Тем не менее, дальнейшее усовершенствование предложенных алгоритмов, а также их реализация на GPU (переборные алгоритмы хорошо подходят для GPU, в отличие от CDCL-алгоритмов, лежащих в основе большинства SAT-решателей), может привести к более хорошим результатам. Кроме всего прочего, в ближайшее время мы планируем встроить в MPI-программу переборный алгоритм с первоочередным обходом ячеек из главной и побочной диагоналей, что также может привести к нахождению частично ортогональных троек с более высокими характеристиками.

Заключение

В статье описаны алгоритмы, с помощью которых были найдены новые комбинаторные объекты: 32 пары ортогональных диагональных латинских квадратов порядка 10 (в дополнение к 20 таким парам, известным ранее) и две тройки взаимно частично ортогональных диагональных латинских квадратов порядка 10 с характеристикой 73 (в дополнение к одной такой тройке, известной ранее). Принципиально новым результатом стало доказательство того факта, что на основе всех 52 известных на данный момент пар ортогональных диагональных латинских квадратов порядка 10 (дополняя каждую пару произвольным третьим диагональным латинским квадратом) невозможно построить тройку взаимно ортогональных диагональных латинских квадратов порядка 10. Также были протестированы переборные алгоритмы генерации диагональных латинских квадратов. Результаты показывает, что у этих алгоритмов есть большой потенциал, в том числе и в направлении их реализации на GPU. При получении всех перечисленных результатов были использованы высокопроизводительные вычисления.

Работа была частично поддержана РФФИ (гранты № 14-07-00403-а, 15-07-07891-а и 16-07-00155-а) и советом по грантам Президента РФ (стипендия № СП-1184.2015.5, грант МК-9445.2016.8). Работа выполнена в рамках государственного задания для Юго-Западного государственного университета на 2014–2017 гг., № НИР 2246.