Принципы и методы определения скалярных материальных параметров теории пластического течения с кинематическим и изотропным упрочнением

На современном этапе разработок и использования ответственных инженерных объектов энергетического машиностроения все более жесткие требования предъявляются к обеспечению прочности, долговечности, надежности наряду со снижением металлоемкости конструкций и компактностью их размещения в ограниченных объемах. Анализ опыта эксплуатации ответственных инженерных объектов энергетического

машиностроения позволяет сделать вывод, что при штатной эксплуатации оборудования и систем, работающих в условиях нестационарного термосилового нагружения, доминирующими деградационными процессами являются многоцикловая (МнЦУ) и малоцикловая (МЦУ) усталость, накопление повреждений в результате ползучести, образование и развитие трещин [1]. При расчетах на прочность и долговечность таких конструкций важная роль отводится экспериментальной базе и соответствующим моделям механики поврежденной среды, позволяющим расчетным путем определять кинетику напряженно-деформированного состояния.

В настоящее время разработка математических моделей состояния сред, ориентированных на эффективный анализ напряжений и деформаций элементов конструкций, является важной составной частью расчетов на прочность и долговечность. Без правильного учета существенных эффектов поведения материалов в реальных условиях эксплуатации конструкции не возможно адекватное обоснование прочности, долговечности, остаточного и выработанного ресурса ответственных элементов высоконагруженных конструкций.

При разработке моделей поведения материалов для обширного спектра внешних нагрузок с широкой областью применимости неизбежно приходится искать компромисс между соответствием модели действительному поведению материала, возможностью и эффективностью применения модели при решении прикладных задач, возможностью определения материальных параметров модели из достаточно просто реализуемых базовых экспериментов, точностью определения этих параметров. Широкая область применимости модели в ряде случаев может явиться причиной снижения точности расчетов, а невозможность точного определения входящих в модель материальных параметров и сложность её реализации при решении прикладных задач может привести к нулевой практической ценности модели.

Таким образом, подлинная ценность модели определяется тем, насколько хорошо она удовлетворяет следующим требованиям: широте охвата существующих явлений и точности, соответствию действительности и удобству применения. Для построения адекватных моделей должен использоваться принцип, заключающиеся в том, что физические механизмы являются основой наилучшего решения. После выявления физических закономерностей, существенных для данного класса рассматриваемых задач, необходимо принять решение, каким образом учесть их влияние при выводе определяющих соотношений. Самый прямой путь состоит в математическом моделировании каждого физического механизма. Однако современный уровень знаний в области поведения конструкционных материалов не достаточен для такого подхода. Поэтому приходится использовать феноменологический подход, но представление о физических механизмах оказывает сильное влияние на форму итоговых уравнений.

В настоящее время публикации по методикам определения материальных параметров моделей термопластичности практически отсутствуют. В имеющихся публикациях (см. например [4]) методики определения материальных параметров заключаются в «подборе» параметров путем минимизации отклонений результатов расчетов от экспериментальных данных, чем и гарантируется однозначность определения материальных параметров.

В данной работе для модели пластического течения с кинематическим и изотропным упрочнением, предложенной в [2] и описывающей процессы деформирования для произвольных сложных режимов нагружения, сопровождающихся вращением главных площадок тензоров напряжений и деформаций, развита экспериментально-теоретическая методика определения материальных параметров и скалярных функций определяющих соотношений теории пластичности.

2.    Основные определяющие соотношения. Методика базового эксперимента

Наиболее адекватной и практически используемой теорией пластического течения является теория, основанная на концепции изотропного и кинематического упрочнения. Ключевую роль здесь играет поверхность текучести и ее изменение в процессе деформирования. Понятие поверхности текучести связано с выделением зоны допустимых состояний материала в пространстве девиатора тензора напряжений. Основные положения рассматриваемой модели термопластичности [3] заключаются в следующем:

• -    компоненты девиатора тензора деформаций e_i ′ _j и их приращений Δ e_i ′ _j являются суммой упругих e_i ′ _j ^e и пластических e_i ′ _j ^p компонент;

• -    постулируется пластическая несжимаемость материала (упругое изменение объема): e i ^p i ≡ 0 ;

• -    рассматриваются упругоизотропные среды, характеризуемые зависящим от температуры Т модулем упругости Юнга E ( Т ) , коэффициентом Пуассона ν ( Т ) (или объемным модулем упругости K ( Т ) и объемным модулем сдвига G ( Т ) );

• -    не учитывается анизотропия упругих свойств, вызванная процессом накопления повреждений;

• -    принимается, что поверхность текучести F_p в пространстве девиаторов напряжений представляет собой сферу (Рис. 1) с радиусом C_p и координатами центра ρ _ij (тензор микронапряжений ρ _ij ):

F p = ( σ′ ij -ρ ij )( σ′ ij -ρ ij ) - C p ² = 0, (1)

где σ′ _ij — компоненты девиатора тензора напряжений. Точка О обозначает начальное положение центра поверхности текучести F_{p 0} с радиусом C_{p 0} недеформированного материала. Радиус C_{p 0} является функцией температуры.

Радиус поверхности текучести C_p изменяется в зависимости от приращения Δχ длины дуги χ траектории пластического деформирования и приращения температуры согласно уравнениям [2]:

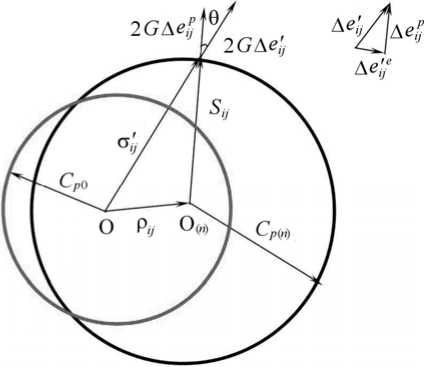
Рис. 1. Поверхность текучести в пространстве девиаторов напряжений

А Ср, = q,Ах Н (FP) + q, А T + a, ( Qs - C,) АхГ (Fp) + А Сот ;

C p = C , о +А C , ;

- qcA V1+(1- A) q q x=----------------

V1A + (1 - A)

х .

;

Q = Q , A y 2 + ( 1 - A ) Q

УS     v 2 A + (1 - A) ;

Fp=P j P i

P max    ⁰ ;

H ( F p ) = 1

¹ при F , = 0 и p j ^P.. >  О О при F , <  0 или Р у Ар _/? . < 0 ’

Г (FP)=1 - Н ( fp) ;

S- = СУ'. i i

P j ;

Ах = 1 3 Аej А ej I ;

t хМ = JxH (Fp) dt;

t

x = J x dt;

A = 1 - cos² 0 ;

cos 0 = n e n j ;

e n i ^e

Ае’

1 ;

( А j e У²

s

nj =

S i

1 ( S i S i )²

,

в которых используются обозначения: при пропорциональном (лучевом)

q, = q, ( x М , Т ) — модуль изотропного упрочнения ^{х х} p

нагружении, где х м_р

—

длина траектории

пластического деформирования на участках монотонного нагружения; qc — модуль упрочнения при нагружении по касательной к поверхности текучести («нейтральное» нагружение при 0 = п/2); q, — модуль, описывающий связь координат центра поверхности текучести и температуры; Q = Q (pmax, T)

—

модуль изотропного

упрочнения при пропорциональных циклических процессах; Qc = Qc (pmax, T) — модуль циклического упрочнения при 0 = п/2, где 0 — угол между вектором приращения девиатора деформации (Ае'^, имеющем направляющие косинусы ne, и нормалью к поверхности текучести; ац ( Qs - C,)

—

модуль циклического упрочнения при

переходных циклических процессах ( а ц = а ц ( Т ) ), где С_р — текущее значение радиуса поверхности текучести; А — отклонение вектора догрузки в точке нагружения от нормали к поверхности текучести; у 1 и у ₂ (0 < V 1 ^ 1,0 < v ₂ ^ 1) — параметры, позволяющие корректировать влияние модулей q _х , q c , Q и Q c на изотропное упрочнение материала. Скалярные функции q _х , Q , q , определяются экспериментально при пропорциональном (лучевом) нагружении. Операторы H ( F _p) и Г ( F _p) позволяют автоматически провести разделение процессов деформирования на монотонные ( H = 1, Г = 0 ) и циклические ( H = 0, Г = 1 ) .

В уравнении (2) первый член описывает изотропное упрочнение в результате монотонного пластического деформирования (H (FP) = 1 и Г (FP) = 0), второй член — изменение радиуса поверхности текучести при изменении температуры, третий член — циклическое упрочнение материала (H(Fp) = 0 и Г(Fp) = 1), последний член — восстановление (возврат) радиуса поверхности текучести в условиях высокотемпературной выдержки (отжига). В целом же уравнение (2) описывает локальную анизотропию пластического упрочнения в зависимости от параметра A .

Модуль изотропного упрочнения q _х учитывает изменение изотропного упрочнения материала в зависимости от направления деформирования в данной точке траектории (Рис. 1), то есть от угла 0 . Имеем при пропорциональном нагружении

0 = 0;    cos 0 = 1; A = 0;   q, = q х;   Qs = Q и при непропорциональном деформировании с углом 0 = п/ 2 (вектор A e перпендикулярен нормали к поверхности текучести в точке нагружения)

A = 1,     q х = q c .

Аналогично, в (4) для циклического изотропного упрочнения при циклическом пропорциональном нагружении 0 = 0 и Q_S = Q , а при циклическом непропорциональном — 0 = п/ 2, Q S = Q c ( p _max, T ) .

При стационарном циклическом деформировании материала с постоянной амплитудой деформации и Т = const (а следовательно, p _max = const, H ( F _p ) = 0, Г ( F _p ) = 1, Q_S = const) радиус поверхности текучести С_p стремится к Q S и параметры петли гистерезиса стремятся к своему стационарному значению, определяемому значением Q_S , которое зависит от текущих значений Т и p _max.

Эволюционное уравнение для изменения координат центра поверхности текучести (тензора p i ) имеет вид [2]:

^Ap и= g 1 ^A e ^- g 2 p ^aX^- g T pJ^A T} + g 0 T p i ,      (^A Т ) = *

' Т

при Т >  0

,          (10)

при Т < 0

где g1 и g2 — модули кинематического упрочнения, являющиеся функциями температуры; g0Т — модуль низкотемпературного отжига. Модуль g1 определяет перемещение центра поверхности текучести в результате приращения тензора пластических деформаций Aе^, модуль g2 — его постепенную релаксацию. Модуль gT, описывающий изменение координат центра поверхности текучести в зависимости от повышения температуры Т, вычисляется по формулам [2]:

_g =- ^{A g1 A} g2- >  0;

8 T g,A T g2 AT    ’ gT = 0 при AT < 0;

^AA max

( p ,Ap _у .) H ( F p )

⁽ p j p j/²

^g 2 ^p max ^AX^- g T p max ( ^A T ) ^- g 0 T p max .

В уравнении (10) первый и второй члены описывают анизотропную часть деформационного упрочнения, третий — эволюцию р i в результате изменения температуры, четвертый — эффекты низкотемпературного отжига. В целом (10) описывает известный пространственный эффект Баушингера и анизотропию векторных свойств при изменении направления деформирования (изломе траектории деформирования). Введение второго члена основано на гипотезе А.А. Ильюшина, заключающейся в том, что упрочнение зависит от истории деформирования лишь на некоторой ближайшей части траектории (запаздывание векторных свойств) и моделирует исчезающую память внутренней переменной р j . Скорость изменения р j является разностью между двумя составляющими: g 1 e p g 1 p e p и g ₂ p j x .

Уравнения (1)–(13) содержат как частные случаи все основные известные формы уравнений теории пластического течения при малых деформациях [2]. Для определения указанных материальных параметров эволюционных уравнений (2)–(13) предлагается следующая система из специальных базовых экспериментов.

Эксперимент 1 . Эксперимент по квазистатическому растяжению–сжатию цилиндрических лабораторных образцов путем жесткого нагружения с контролем остаточной деформации на рабочей части образца при скоростях деформации e_u ~ 10~² сек^-1 (Рис. 2). По результатам эксперимента при базовых постоянных температурах Т j определяются диаграмма деформирования (кривая 1 ) и геометрическое место обратных пределов текучести при сжатии G - i (кривая 2 ) с заданным допуском на остаточную деформацию ∆ после растяжения до некоторых значений деформаций ( e ₁ ^p ₁¹ , e ₁ ^p ₁² ,…, e ₁ ^p ₁ ⁿ ), где n — число циклов нагружения. С использованием экспериментальных кривых 1 и 2 получают экспериментальные зависимости напряжения при растяжении G 11 и обратных пределов текучести о - ^ ' ) от пластических деформаций e 1p (Рис. 3), а также функции C_p ( х ) , р 11 ( х ) при различных базовых температурах T j .

В случае одноосного растяжения-сжатия e 1 p = х , а уравнение поверхности текучести будет иметь вид:

Р| G 11 — Ц Р .1 ] = C p • (14)

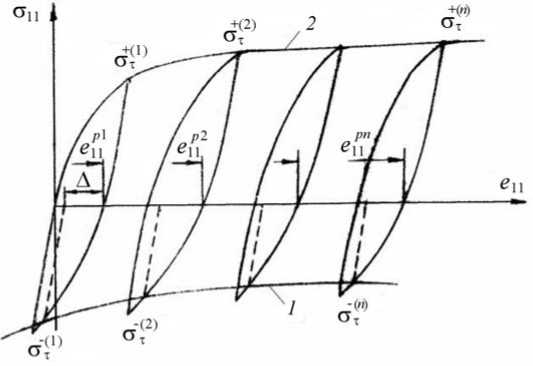
Рис. 2. Базовый эксперимент на термопластичность

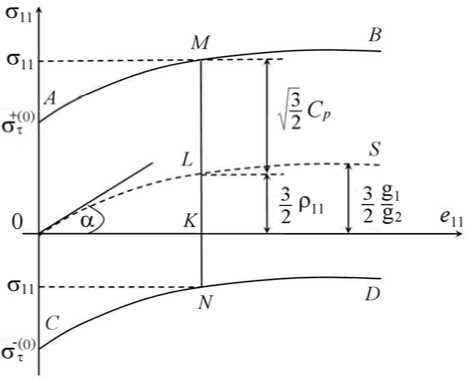
Рис. 3. Зависимость напряжения одноосного растяжения и обратных пределов текучести от пластической деформации

Радиус поверхности текучести и координаты ее центра определяются как

2^1 +5           2        + ( ° )

С р 3^ 2 ^{G |1},       С Р ° 3 з ^Q ,

P11 = g^- (1 - e " g2Х), g2

+ ( i )

Q где 5 = —-7^ — мера эффекта Баушингера.

QT

Материальные параметры в уравнениях (2), (3) и (10), описывающих монотонное упругопластическое деформирование, вычисляются по формулам:

• g i = з • tg ^а ;

_ Cp ⁽х ) q^x м^м "  ^х p

g, = ³ • -g- ;

2         max

² P ii

g ₁   2 _max

• — = ^^p-. ;

g 2    3

На основе значений g ₁ и g ₂ из соотношений (11) и (12) находится модуль g_T .

Материальные параметры данной модели термопластичности определяются для каждой выбранной базовой температуры T_j , при которой экспериментально определены кривые AB и CD (Рис. 3). Для одной температуры испытывается не менее трех образцов.

Эксперимент 2 . Испытания на одноосное циклическое блочное жесткое изотермическое нагружение с постоянной амплитудой деформации (полной или остаточной) в пределах блока нагружения и возрастанием (убыванием) её при переходе к следующему блоку (Рис. 4).

Число блоков нагружения при увеличении (или уменьшении) амплитуды деформации равно 3–6. Число циклов в каждом блоке определяется условием стабилизации параметров петли гистерезиса. Число повторных опытов при одинаковых наборах блоков нагружения составляет не менее трех.

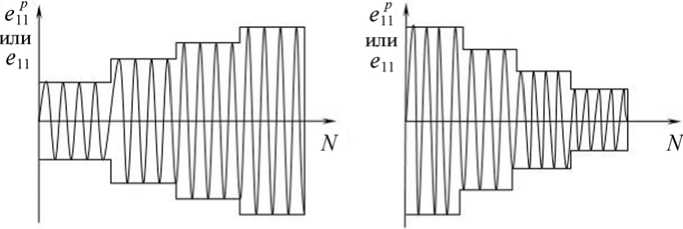
Рис. 4. Базовый эксперимент для определения материальных параметров циклического упругопластического деформирования

По результатам экспериментов определяются зависимость Q S ( p max ) и параметр а ц при различных базовых температурах T_j , входящие в уравнения (2) и (5), а также зависимость:

– площади петли гистерезиса (работы, затраченной на пластическое деформирование) от числа циклов: S ( N );

– максимального и минимального значений напряжения в цикле от числа циклов: σ max ( N ) и σ min ( N );

– ширины петли гистерезиса (размах остаточной пластической деформации в цикле) от числа циклов: Δ е ( N ).

3.    Техническое обеспечение проведения базовых экспериментов

Для проведения базовых экспериментов необходимо использовать лабораторные образцы со сплошной или полой (толщина стенок 2 мм) цилиндрической рабочей частью диаметром 10–20 мм и длиной 30–40 мм. Форма образцов должна обеспечивать в рабочей части однородное распределение полей деформаций, напряжений и температур.

Особое внимание должно быть уделено технологии изготовления образцов. Основные требования к технологии заключаются в следующем.

Образцы должны изготавливаться из заготовок, отобранных из статистически представленных партий материала для определения физико-механических характеристик материала. Вырезка заготовок и технология изготовления образцов не должна оказывать существенного влияния на структурное состояние металла рабочей части, изменения которого могут привести к изменению сопротивления материала усталости (изменению долговечности в результате изменения структуры материала). Наклеп поверхности рабочей части образца при обработке должен быть минимален за счет выбора оптимальной глубины резания на промежуточных и, особенно, на заключительных операциях, а нагрев образца не должен вызывать структурных изменений в материале его рабочей части. Поверхность рабочей части после механической обработки не должна иметь следов трещин, цветов побежалости, рисок и других дефектов. Заключительные операции по чистовой обработке (тонкое точение, шлифование, полирование и притирка) должны сводить к минимуму деформацию поверхностного слоя образца. Должна быть обеспечена плавность перехода от рабочей части образца к его концевым частям за счет применения соответствующих способов обработки (точение по контуру, профильное шлифование и так далее). Переход от рабочей части к галтели должен выполняться с гладкой частью за одну технологическую операцию. Не должно допускаться повреждение рабочей части образца измерительным инструментом. Для серии однотипных испытаний технология изготовления образцов должна быть одинаковой. Исследуемая партия образцов должна быть снабжена сертификатными данными (химический состав, структурное состояние металла, термическая обработка и прочее).

Вышеперечисленные базовые эксперименты необходимо проводить на экспериментальных комплексах, которые отвечают следующим требованиям: – обеспечивают жесткое закрепление образцов в захватах машины;

– осуществляют измерение деформации непосредственно на рабочей части образца;

– предоставляют возможность программно задавать закон нагружения лабораторного образца по деформации (полной и остаточной) на рабочей части, перемещению активного захвата или нагружающему усилию (напряжению);

– имеют термокамеру и высокотемпературный экстензометр для проведения испытаний в диапазоне эксплуатационных температур;

– обеспечивают равномерное распределение температур в пределах рабочей части образца;

– хранят и воспроизводят экспериментальную информацию.

4.    Экспериментальные и численные результаты

По разработанной методике из базовых экспериментов получены материальные параметры эволюционных уравнений термопластичности при монотонном упругопластическом деформировании для конструкционных сталей 15Х2МФА и 08Х18Н10Т.

Лабораторные образцы (Рис. 5) были изготовлены из металла одной партии и плавки. Общая длина образца составляла 180 мм, диаметр рабочей части — 12 мм. Форма данного образца обеспечивала в рабочей части однородное распределение полей деформаций, напряжений и температур.

Базовые эксперименты — испытания по построению диаграмм квазистатического монотонного растяжения–сжатия образцов сталей 15Х2МФА и 08Х18Н10Т, проводились при температуре 20 ° С при «жестком» пошаговом деформировании (растяжении-сжатии) рабочей части образца на универсальной испытательной машине МИУ-200.1КТ (предприятие–изготовитель НИКЦИМ Точмашприбор, г. Армавир). Испытуемый образец растягивался до деформации е ₁ ^р ₁ = 0,03. Пошаговое сжатие образцов производилось при значениях деформации е ₁ ^р ₁ : 0,002; 0,004; 0,006; 0,008; 0,01; 0,015; 0,02; 0,025; 0,03. Допуск на остаточную деформацию ∆ при определении обратных пределов текучести составлял 0,05%. При заданном значении температуры испытывалось по три образца для каждой марки стали. Экспериментальные кривые для сталей 15Х2МФА и 08Х18Н10Т приведены на рисунке 6. По этим кривым затем определялись значения материальных параметров термопластичности рассматриваемых сталей (Таблицы 1 и 2).

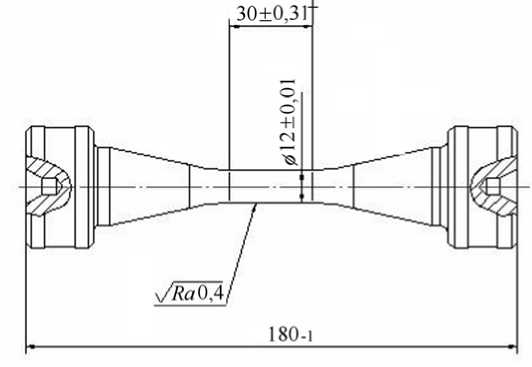
Рис. 5. Эскиз образца

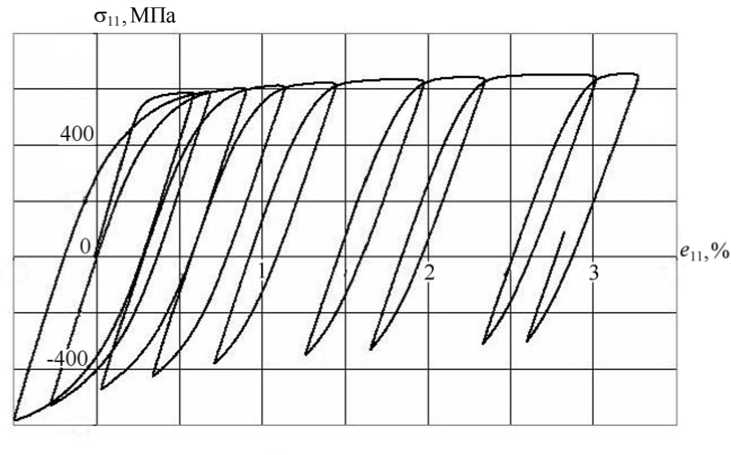
а

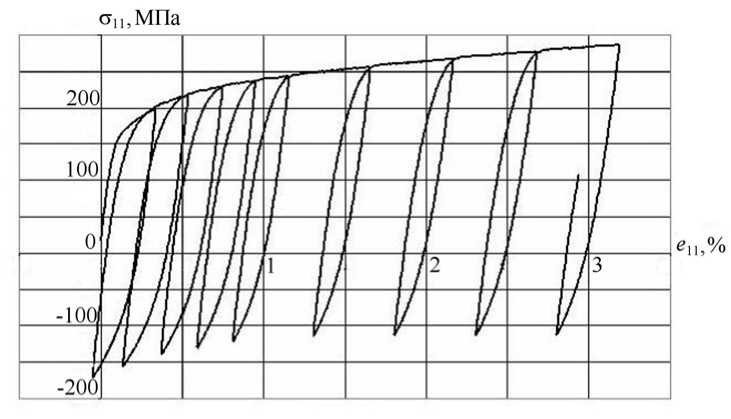
б

Рис. 6. Диаграммы деформирования для образцов из стали 15Х2МФА ( а ) и стали 08Х18Н10Т ( б ) при температуре 20ºС

Таблица 1. Значения модулей кинематического упрочнения при температуре 20ºС

Марка стали	g 1 , МПа	g 2 , МПа
08Х18Н10Т	24910	358,9
15Х2МФА	128700	689,5

Таблица 2. Значения модуля изотропного упрочнения в зависимости от длины пути пластического деформирования при температуре 20ºС

χ 1	0 1	0,003	0,006	0,009	0,012	0,015	0,018	0,023	0,03
Сталь 08Х18Н10Т
q χ , МПа	–16000	–2276	854,8	854,8	854,8	854,8	854,8	854,8	854,8
Сталь 15Х2МФА
q χ , МПа	–139600	–15120	-1673	562	562	562	562	562	562

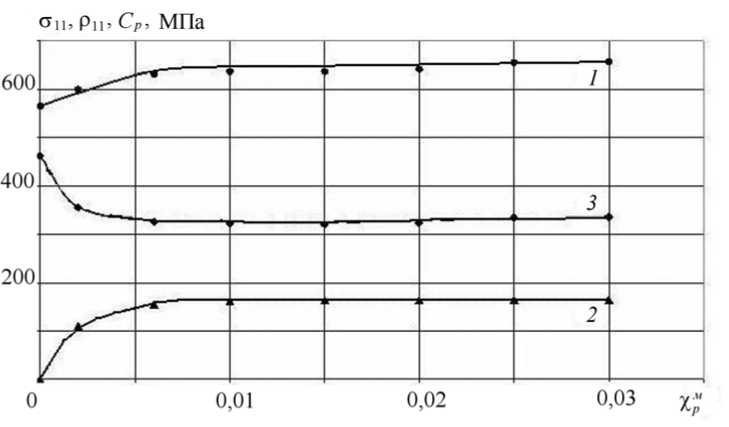
а

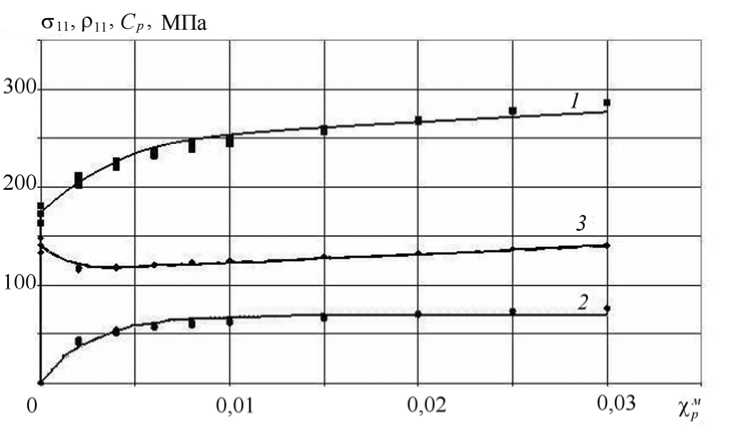
б

Рис. 7. Расчетная зависимость изменения напряжения одноосного растяжения и параметров поверхности текучести от длины пути пластического деформирования при монотонном растяжении образца из стали 15Х2МФА ( а ) и стали 08Х18Н10Т ( б ) ( 1 – σ ₁₁ ~ χ ^м _p ; 2 – ρ ₁₁ ~ χ ^м _p ; 3 – С _р ~ χ ^м _p )

Для оценки адекватности применяемых зависимостей и методики определения материальных параметров эволюционных уравнений термопластичности проведено численное моделирование базового эксперимента. На рисунке 7 представлены расчетные диаграммы деформирования, а также зависимости радиуса поверхности текучести и координат центра поверхности текучести от длины пути пластического деформирования χ при монотонном растяжении образцов из сталей 15Х2МФА и 08Х18Н10Т, на которых данные, полученные при проведении «базового эксперимента», отмечены соответствующими маркерами. Анализируя экспериментальные данные и сравнивая их с расчетными (см. Рис. 6, 7), можно сделать вывод об адекватности методики определения материальных параметров используемых зависимостей термопластичности. Разность экспериментальных и расчетных данных на участке относительной пластической деформации от 0 до 3%, не превышает 4%.

5.    Заключение

Предложена математическая модель пластического течения с кинематическим и изотропным упрочнением, описывающая процессы сложного пластического деформирования в конструкционным материалах (металлах и их сплавах). Разработанная модель позволяет учесть: монотонное и циклическое упрочнение, а также эффекты циклической памяти материала при пропорциональном и непропорциональном деформировании, включая переходные циклические процессы и стабилизированное циклическое поведения материала; локальную анизотропию пластического деформирования при изломе траектории деформаций.

Развита экспериментально-теоретическая методика определения материальных параметров и скалярных функций развитых определяющих соотношений. Сформулированы требования к техническому обеспечению проведения базовых экспериментов. Экспериментально определены значения материальных параметров определяющих соотношений термопластичности для сталей 15Х2МФА и 08Х18Н10Т.

Проведено сравнение результатов вычислительного и натурного экспериментов и сделана оценка степени адекватности применяемых соотношений и методики определения материальных параметров.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 09-08-00266-а).