Проблемы когерентного описания реакций переноса электрона

Часто реакции переноса электрона в конденсированных средах описываются в рамках стохастического подхода [1], [2]. Уравнения Зусмана для двухуровневой системы имеют вид:

dp,.     r       . V ..

д     ^1 Pll "*"Z Т (Р12 ~ P2I X(1)

otп

5р„         -V ГX

L9P22 1 . (Р12 Р21)>

OtЯ д " — ^-Pl2 (Ри — Р22)"*"Т (^1 — ^г)Р12 ,

Ot           ПП

		д2^	dU,	d , _	8
где	А=—		+—'-	— +квГ
		[ dq"	dq	dq	8g" j

Ч кв

Т

Я

Е_г оператор L

U,

• —    диффузионный оператор для /-го состояния;

• —    продольное время диэлектрической релаксации;

• —    константа Больцмана;

• —    температура;

• —    координата реакции;

• —    энергия реорганизации;

• —    полусумма диффузионных операторов первого и второго состояний;

• —    энергетические поверхности базисных состояний.

* Работа была поддержана грантом РФФИ № 05-03-32680.

Данный подход применялся многочисленными авторами для описания задачи переноса электрона для различных моделей растворителей (см. [3]—[6] обзор [7] и приведенные там ссылки).

Обычно уравнения Зусмана решаются в приближении о локализации недиагональных элементов матрицы плотности в окрестности пересечения термов и исключением из исходной системы уравнения на недиагональные элементы [1]

<р₂1 ~ Ри)^{= 2л/к}<рц ~ p^w ^- я), (4) где q_c — точка пересечения диабатических термов.

Хотя этот прием обладает мощными регуляризующими свойствами, оказывается потерянной всякая информация об эффектах квантовой интерференции состояний. При этом сколько-нибудь подробное описание когерентных квантовых эффектов становится невозможным. Отметим, что в связи с развитием точности и чувствительности современной экспериментальной техники описание этих эффектов становится особенно актуальным.

Кроме того, известно, что в некоторых частных случаях полная система уравнений Зусмана приводит к нефизичным результатам, таким как появление отрицательных населенностей и т. д.

В статье [8] Французов предложил использовать для исследования области применимости полной системы уравнений Зусмана соотношение Фон Неймана для элементов матрицы плотности:

Р11МР22СМ) ^ |р)2 (Х^)Г • (5)

Решая задачу на прямых термах

U_x= Fx, и_г= —Fx, У = 0,                              (6)

где           F — наклон термов;

при начальных условиях

РцС^ 0) = р₂₂(х, 0) = р₁₂(х, 0) = 0,56(q - q₀\                           (7)

легко получить d0 =

p11(x,?)p„(x,0

_ 2F² , = exTx-Dt—- t" - Зй²Д

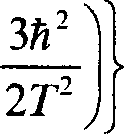
Таким образом, уравнения Зусмана не пригодны для описания эволюции системы на временах/<т/г=          [8].

• 2.    Уравнения Вигнера — Фоккера — Планка

Заметим, что подход Зусмана основывается на уравнении Смолуховского, описывающем диффузию в потенциале. Известно, что это уравнение может использоваться только на временах существенно превышающих время свободного пробега частицы. Для описания движения частицы на меньших временах необходимо учитывать эволюцию распределения по координатам и импульсам и пользоваться уравнениями типа Фоккера — Планка — Крамерса или более общими [9]. Это соображение кажется разумным и, казалось бы, объясняет проблемы, возникающие при анализе решений на малых временах, которые выглядят как «плата» за потерю информации об импульсном распределении- Таким образом, мы можем принять в качестве рабочей гипотезы необходимость рассмотрения на временах Кт_р эволюции импульсного распределения для не противоречивого описания эволюции системы.                                ■

Такое рассмотрение можно провести на основе результатов работ [ 10], [ 11 ]. В случае гармонического или линейного потенциала в представлении Вигнера [12] система уравнений для двухуровневой системы имеет вид:

(9) dth

^<ЬР^ = ]Ц^^

ЩМА = Ц^^^(11)

Stn где

L, = -P-- +---!----="

dq dp\_dq 2

^Р^к.т^-Ци.-иХ др        Эр n

В работе [11] эта система уравнений получила название ВФП система (Wigner — Fokker — Planck equations).

Уравнения Зусмана (1)—(3) можно получить из этой системы в пределе сильного трения и больших температур (см. напр. [10], [11]).

Проводя для уравнений (9)—(11) анализ, аналогичный описанному в разделе 1, легко получить следующий результат. Отношения матричных элементов Ai), на временах Z < т, где т = 1/у возрастает экспоненциально с показателем 3F²/%^k_BT. Таким образом, оказывается нарушенным условие фон Неймана на элементы матрицы плотности, и ее положительную определенность уже нельзя гарантировать.

Из этого мы делаем вывод о невозможности рассматривать систему уравнений (9)—(11) как существенное улучшение уравнений Зусмана.

• 3.    Приведение уравнения Калдейры-Лэггетта к форме Линдблада

Исторически уравнения Зусмана были предложены из эвристических соображений. Однако в последующие годы был проведен ряд исследований [10], [13]—[15], в которых были предприняты попытки их вывода из «первых принципов». Таким образом, уместно обратится к этим работам для преодоления пробелов теории.

Так, в [10] авторы исходили из уравнений, полученных в работе [15]. В последней для системы, связанной с термостатом, было получено уравнение:

^ = “[#S’p]-^[<7^pFjkW^              (12)

Важно отметить, что данное уравнение не принадлежит к так называемому классу уравнений Линдблада [16], [17].

^ = "[я«,р]-5^Др-2Др^ + р£^             (13)

где           Ц — операторы, описывающие взаимодействие системы со средой;

Я — гамильтониан системы, вообще говоря, перенормированный в результате взаимодействия со средой.

Данное уравнение обобщает уравнение Лиувилля и является наиболее общим видом уравнения, сохраняющим положительную определенность матрицы плотности [18].

Уравнение (12) приводится к желаемой форме добавлением дополнительного слагаемого (см. напр. [19])                                                                                      .

^ = -|[77s-p]--^[U?,pFy[?4Ap}]-y[H^p]L          (14)

ot п         п"           й            2

где           Q₆ = f№D\D = -lkJh.

В [19] предлагается рассматривать взаимодействие системы с резервуаром как процесс непрерывного измерения. В результате последовательных измерений положение частицы разрешается средой с все большей точностью. В силу принципа неопределенности Гейзенберга этот процесс должен вызывать изменение сопряженного координате импульса. Именно это и обеспечивает дополнительное слагаемое в (14). Таким образом, физический смысл добавленного слагаемого состоит в обеспечении согласования динамики частицы с принципом неопределенности Гейзенберга [19].

Переходя к представлению Вигнера с помощью соответствий Боппа (Ворр) [12], получим модифицированную систему уравнений (9)—(11), где операторы диффузии содержат дополнительное слагаемое:

=/,у+хд7’ где у = 2Б2Оо.

Применяя к полученным уравнениям вышеизложенный анализ и вводя безразмерное время т = Гу, легко получить:

г(т) = ехр

IF¹ (

.У ² кА

АМ

2Х2

АМ ,

1 + V УХХ,тН1+т+т²Ау.

. (т(2+т) + Х2(т2+2те"т-2 + 2^т))2+Х2(т-1 + е"т)2

(Л,Т ) —------------------------~--------------------------------------

2т(1 + Х2)-(1-е"т)(3-е )

Поведение при малых временах определяется значением управляющего параметра X = 2£77yh. При X < 1 получаем экспоненциальный рост отношения. Однако при           .

Х>1                                     (18)

получаем экспоненциальное затухание на малых временах. Отметим, что данный критерий отличается от полученного в [8] и носит условный характер (соотношение энергетики тепловых флуктуаций и диссипации), в то время как промежуток времени т/г не может быть устранен специальным выбором параметров модели.

• 4.    Выводы

Предлагаемый подход можно использовать для описания когерентных явлений при соблюдении условия (18). Очевидно, что выполнение этого условия предполагает предел больших температур. Таким образом, время декогеренции будет малым и, как следствие, за характерное время декогеренции будет происходить разрушение недиагональных по координате элементов матрицы плотности на терме р^д, д', t). Это малосущественно вдали от области пересечения диабатических термов, так как именно в ее окрестности квантовые переходы эффективны и учет когерентности важен.

Очевидно, здесь скрыт существенный недостаток модели, так как фактически термическая декогеренция обеспечивает в этой модели своевременное разрушение недиагональных по диабатическому базису элементов матрицы плотности, в то время как их релаксация должна обеспечиваться независимым механизмом, учитывающим не только взаимодействие со средой, но и особенности взаимного расположения энергетических поверхностей базисных состояний. При таком описании, на наш взгляд, можно было бы ослабить требование высоких температур и изучать когерентные явления при менее жестких условиях.

Автор благодарит профессора А.И. Иванова за ценные замечания и советы, а также С.В. Фесь-кова за помощь в подготовке работы к публикации.