Проекционный метод нелокального улучшения в дискретно управляемых систем

Автор: Дрыганова Екатерина Вячеславовна

Журнал: Вестник Бурятского государственного университета. Математика, информатика @vestnik-bsu-maths

Рубрика: Управляемые системы и методы оптимизации

Статья в выпуске: 1, 2015 года.

Бесплатный доступ

Рассматривается метод нелокального улучшения в задачах оптимального управления дискретными системами на основе операции проектирования на множество допустимых значений управления. Эффективность метода иллюстрируется на дискретных аналогах непрерывных тестовых задач.

Проекционный метод, нелокальное улучшение, дискретная система

Короткий адрес: https://sciup.org/14835130

IDR: 14835130

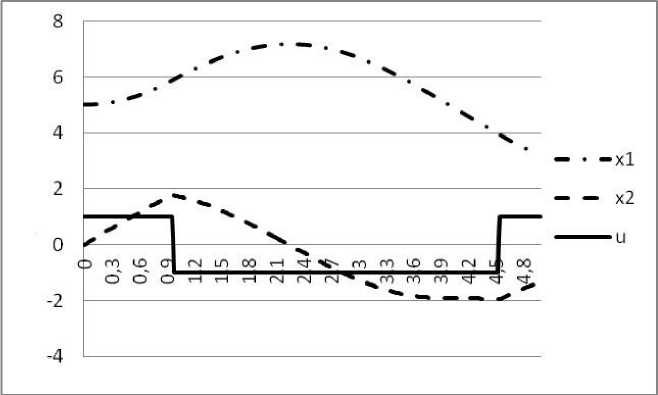
Список литературы Проекционный метод нелокального улучшения в дискретно управляемых систем

Булдаев A.C. Методы возмущений в задачах улучшения и оптимизации управляемых систем. -Улан-Удэ: Изд-во Бурятского госуниверситета, 2008. -260 с.
Булдаев A.C., Моржин О.В. Модификация метода проекций для улучшения нелинейных управлений//Вестник Буряткого государственного университета. -2010. -Вып. 9: Математика и информатика. -С. 10-17.
Моржин О.В. Методы нелокального улучшения в задачах оптимального управления на основе точных формул приращения функционала//Программные системы: теория и приложения: электронный научный журнал. -2010. -№4(4). -С. 67-83.
Моржин О.В. Вычислительные аспекты нелокального улучшения управления в дифференциальных системах//Программные системы: теория и приложения: электронный научный журнал. -2011. -№2(6). -С. 37-51.
Горнов А.Ю. Вычислительные технологии решения задач оптимального управления. -Новосибирск: Наука, 2009. -279 с.

Статья научная