Проект элективного курса по математике, как средства адаптации старшеклассников к вузу
Автор: Титова Ю.А.
Журнал: Форум молодых ученых @forum-nauka
Статья в выпуске: 12-4 (28), 2018 года.
Бесплатный доступ
В данной статье приведен проект элективного курса по математике, как средства адаптации старшеклассников к ВУЗу.
Элективный курс, адаптация, матрица, система линейных уравнений
Короткий адрес: https://sciup.org/140281657
IDR: 140281657
Текст научной статьи Проект элективного курса по математике, как средства адаптации старшеклассников к вузу
Одним из важнейших направлений модернизации системы образования в России становится переход к старшей профильной школе.
Выпускнику основой ступени необходимо совершить ответственный выбор профилирующего направления собственной деятельности. Будет ли дальнейшая судьба его связана с математическими науками, пойдёт ли он учится в вуз, какой видит он свою профессию, решается в школе в 10—11 классе.
Представляется целесообразным освоение учащимися предметноориентированного элективного курса по изучению матриц в 11 классе т. к. предлагаемый курс является развитием системы ранее приобретенных программных знаний и приоткрывает занавес во внешкольную математику. На изучение курса отводится 34 часа.
Цель курса — создать целостное представление о теме «Системы линейных уравнений», которой в школьной программе уделено не достаточно времени.
Задачи курса — дополнить базовую программу новыми понятиями, не нарушая ее целостности, расширяя и углубляя знания учащихся; воспитать интерес к предмету через нетрадиционные формы работы, подачи материала, возможность свободного творчества.
Курс является элементом преемственности между школой и вузом. Программа содержит три блока, связанных единой идеей.
Первый блок систематизирует ранее полученные знания арифметических действий с целыми числами, знакомя с новыми понятиями: матрица и действия с матрицами.
Второй блок вырабатывает навыки вычисления определителя второго и третьего порядка и нахождения матрицы, обратной данной.
Цель третьего блока — показать практическую значимость первого и второго блока при решении систем линейных уравнений.
В результате изучения данного курса учащиеся знают:
-
- типы и формы матриц;
-
- матричную символику;
-
- действия над матрицами;
-
- понятие определителя и его свойства;
-
- методы решений систем линейных уравнений. Умеют:
-
- складывать, перемножать матрицы;
-
- решать системы линейных уравнений методом Крамера, Гаусса, методом обратной матрицы.
Предполагаются следующие формы организации обучения:
-
- индивидуальная (консультации, тесты),
-
- групповая (исследовательские работа, творческие работы),
-
- коллективная (беседы, практикумы, игры),
-
- взаимное обучение (консультации, взаимообмен заданиями, работа в парах), свободная комплектация групп по желанию,
-
- самообучение (работа с учебной литературой, задания по образцу), - саморазвитие (подготовка сообщений на выбранную тему, работа с информационным и методическим материалом).
Занятия включают в себя теоретическую и практическую части.
Домашние задания носят вариативный характер: каждый ученик по желанию может выбрать либо выполнение практической части, либо изучение теории, либо творчество: самостоятельное создание заданий, сообщений, плакатов. При этом творческое задание может быть выполнено группой учащихся.
Эффективность обучения отслеживается следующими формами контроля:
-
• самостоятельная работа;
-
• срезы знаний, умений в процессе обучения;
-
• защита творческих заданий
Показателем эффективности обучения можно считать растущий интерес к математике, творческую активность, улучшение результатов успеваемости учащихся.
Оценивание самостоятельных работ производится по системе «зачёт \ незачёт», тестовые работы по 100 бальной системе, на творческие и исследовательские работы вводится рецензирование.
Итоги реализации учебной программы подводятся на заключительном занятии в форме конференции.
Тематическое планирование
|
Тема |
Кол-во часов (теор./ практ.) |
Форма занятий |
Вид контроля |
|
I. Матрицы и операции над ними Определение матрицы. Сложение и вычитание матриц. Умножение матрицы на число. Произведение матриц. Единичная матрица. Экскурс в историю |
10 (3\7) 1 4 4 1 |
Лекция. Практикум, Занятие-иссле дование. Занятие-турнир. Конференция |
Тестовые задания. Изготовление плакатов. Творческое задание- историческая справка. |
|
II. Определители квадратных матриц Определители II и III порядка. Матрица, обратная |
9(2\7) 5 4 |
Семинары. Занятия- взаимообучения. Практикумы консультации |
Результаты сам. работы. Тесты. Наблюдение. |
|
данной. |
|||
|
III. Системы линейных урав нений Основные понятия. Методы решения систем Метод Крамера. Метод обратной матрицы. Метод Гаусса. Решение систем |
13(4\9) 1 1 3 3 3 2 |
Беседа. Занятие-исследование. Практикумы. Дидактические игры |
Подготовка докладов и сообщений. Вариативная самостоятельная работа. Самооценка. Взаимооценка |
|
IV. Итоговое занятие |
2 |
Учебно-практическая конференция |
Практ. работа |
Содержание программы
Тема 1. МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ
На первом занятии сообщить учащимся значение и цели элективного курса. Повторить правила сложения, вычитания, деления и умножения положительных и отрицательных чисел. Дать определение матрицы, обозначение и виды матриц. На втором занятии рассмотреть и научить выполнять сложение, вычитание и умножение матрицы на число. Далее продолжить выполнять действия с матрицами и научить умножать матрицы. Ввести понятие единичной матрицы. Сформулировать свойства матрицы. Решение задач. Подобрать литературу по истории развития линейной алгебры.
Тема 2. ОПРЕДЕЛИТЕЛИ КВАДРАТНЫХ МАТРИЦ
На первом занятии дать определение детерминанта второго и третьего порядка, его обозначение и правила вычисления. Отработать навыки вычисления определителей и нахождения матрицы, обратной данной.
Разложение определителей по элементам ряда. Минор и алгебраическое дополнение ввести для сведения. Интересно рассмотреть задания на нахождение неизвестных в одном из рядов по известному значению определителя.
Тема 3. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ И ТРЕМЯ НЕИЗВЕСТНЫМИ.
Дать определение систем уравнений первой степени. Вспомнить методы решения систем, изученные в школе. Сформулировать методы Крамера, Гаусса, метод обратной матрицы при решении систем двух линейных уравнений с тремя неизвестными. Выработать навыки решения систем. Рассмотреть составление систем по матрице. Организовать самостоятельную работу учащихся с литературой.
ИТОГИ РЕАЛИЗАЦИИ УЧЕБНОЙ ПРОГРАММЫ подводятся на заключительном занятии в форме конференции, где учащиеся представляют результаты своей работы.
Основные понятия курса
Произвольная система чисел из некоторого множества, расположенная в виде прямоугольной таблицы, содержащей m строк и n столбцов, называется матрицей.
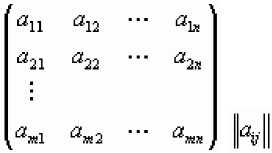
Две матрицы называются равными, если число строк и столбцов у них соответственно равны.
Если число строк матрицы равно числу её столбцов, то такая матрица называется квадратной, а это число порядком матрицы.
В =
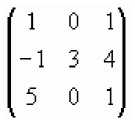
- матрица третьего порядка
Пусть даны матрицы
А =
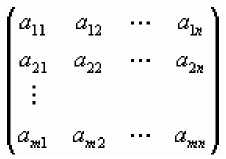
и В =

Произведением А на число с называется матрица
С =

Пример
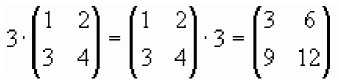
Суммой матриц А и В называется матрица:
С = А + В =
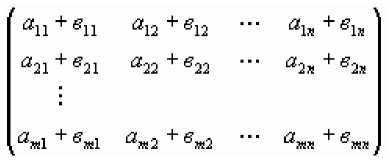
Пример
А =

В =

А + В =
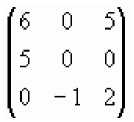
Для матриц
выполняются
все свойства
действий с рациональными
числами.
Произведением матрицы А на матрицу В называется матрица
С11 С12 "■ С1я
С21 С22 "■ С2я
С =
См1 С™2
смн
, где
С11 а11е11 + й12е21 + ■ + ^a^al
С21 = й21е11 + Д22е22 + ■■■ + ^2я^я2
= «иЛя + йИ2^2я + + V»,
Пример:
' 1 2
-2 1
1 "I
з Г 2
-2 ■ 3
2 4
Г
О
г20 5 '
-9 О
Квадратная матрица, все диагональные элементы которой равны 1, а остальные 0 называется единичной.
Г1 О ■■■ О1
О 1 О
Е =
Матрицы, имеющие вид

называют диагональными.
Матрица, которая получается
из данной матрицы заменой строк столбцами, называется транспонированной по отношению к данной.
Определителем n порядка матрицы А называется алгебраическая сумма n! Слагаемых, каждое из которых представляет собой произведение n множителей, взятых по одному и только по одному из каждой строки и каждого столбца матрицы А.
А = V
йи
Й21
Йт1
й12
й 22
m 2
«1П
Й2и

определитель.
Некоторые способы вычислений определителей:
1) Определитель 2-ого порядка
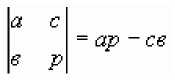
Пример:
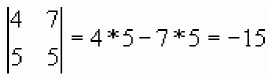
2) Определитель 3-его порядка
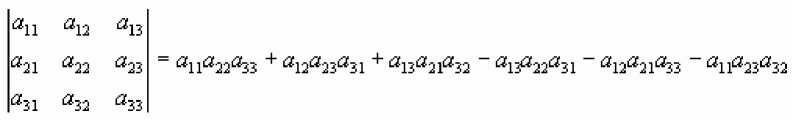
Данный
правило
способ называется правило элементарных преобразований или Саррюса. Оно действует и для определителей более высоких
порядков, но является очень громоздким.
Пример:
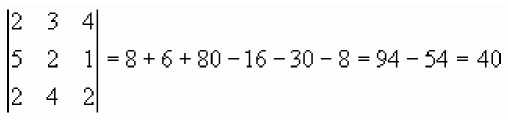
-
3) Определители n-ого порядка.
Минором у элемента у определителя

называется
определитель, который получается из данного вычёркиванием строки и столбца, проходящих через данный элемент.
Алгебраическим дополнением
элемента 4 определителя n-ого порядка называется минор
у этого
элемента,
взятый со знаком
.
Пример. Пусть

.
Найдём
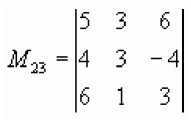
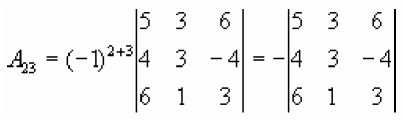
Правило 1. Если в определите n-ого порядка все элементы I-ой строки (j-ого столбца), кроме ^ равны нулю, то такой определитель равен произведению элемента ЙУ на его алгебраическое дополнение.
Пример.
1 1 1
3 1 1
1 3 1
1 1 3
1 Д =
Вычислить определитель
Преобразуем определитель так, чтобы все элементы четвёртого столбца, кроме первого равнялись нулю. Для этого умножим все элементы первой строчки на –1 и сложим со второй и третьей, затем умножим первую строчку на – 3 и сложим с четвёртой. В результате получим
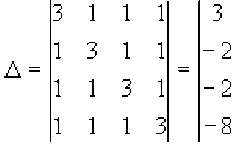
1 1 1
2 0 0
0 2 0
-2 -2 0
Затем, применяя правило, получим:
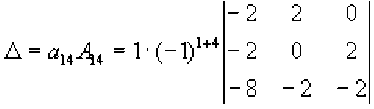
-2 2 О
-2 0 2
-8 -2 -2
Прибавляя к третьей строчки вторую, получим
-22 О
Д=--2 0 2
-8 -2 -2
-2 2 0
-2 0 2
-10 -2 О
- 2(-1)м
- 2
-10
2 -2
= 2'
-2 -10
- 2
= 2(4+ 20) =48
Правило 2. Определитель n-ого порядка равен сумме произведений всех элементов произвольной его строки на их алгебраические дополнения.
Разложение определителя
Л = 3^41 +fli242 + ... + ^4, =
(ЧГ1^^ +(-l)i+X^2 +... + (-l)i+^iH^iH
Пример. Вычислить
3 4
2 1
4 2
Вычислим определитель, разложив его сначала по элементам третьей строки, затем по элементам второго столбца.
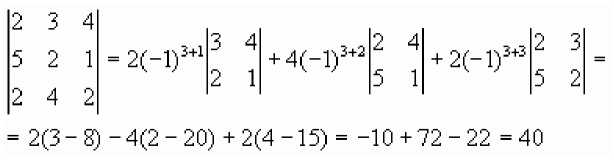
Список литературы Проект элективного курса по математике, как средства адаптации старшеклассников к вузу
- Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах. - М.: Высшая школа. 1997.
- Натансон И. П. Краткий курс высшей математики. - М.: Наука. 1968.
- Письменный Д. Т. Конспект лекций по высшей математике. - М.: Айрис-пресс, 2005.
- Шнейдер В. Е. и др. Краткий курс высшей математики. - М.: Высшая школа. 1972.


