Проект трансарктической железнодорожной магистрали: коалиционный анализ взаимодействий инвесторов

Проблема транспортного освоения северовосточных регионов исторически всегда была актуальна для России [1–3]. Сегодня в ходе гибридной войны с коллективным Западом ситуация обострилась как с точки зрения внешней военной угрозы со стороны США и Канады [4], так и возрастающей внутренней потребности в ресурсах Арктического шельфа. В этой связи актуальным становится вопрос о масштабном строительстве Трансполярной магистрали и, прежде всего, ее западного крыла от Салехарда до Норильска (см. рисунок) по трассе сталинской железной дороги [3], ныне восстанавливаемой низкими темпами и отдельными участками в составе проекта СШХ (Северный Широтный Ход).

Настоящая статья есть попытка ответить на поставленный вопрос и предложить некоторые методы оценки указанного проекта на ранней стадии его реализации, т. е. на этапе структуризации проектных замыслов.

Предположим, что финансирование стройки осуществляется частными компаниями – строительными подрядчиками через госкорпорацию ОАО «РЖД», т. е. холдинг является Заказчиком и эксплуатантом построенной магистрали. Его задача определить доли частных подрядчиков таким образом, чтобы так называемая аллокативная1 эффективность была максимальной [4].

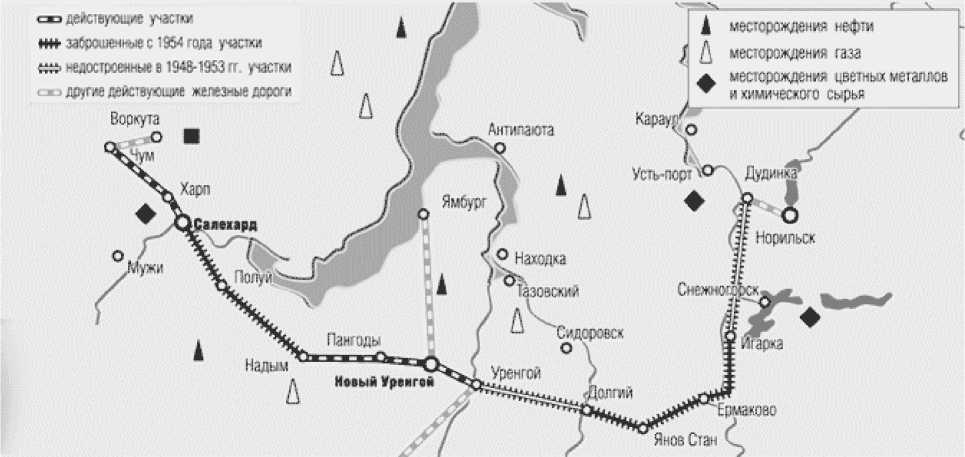
Карта-схема Трансполярной (ТМ) железнодорожной магистрали [3]

Постановка проблемы

В рамках выдвинутых предположений рассмотрим пример [5], где право на заключение договора с Заказчиком получили: «Газпром» (далее – 1), «НОВАТЭК» (далее – 2), «Газпромнефть» (далее – 3), Внешэкономбанк (далее – 4), Внешторгбанк (далее – 5). Предположим далее, что три независимые группы экспертов Заказчика ранжировали данные организации по указанному выше критерию следующим образом:

1 > 4 > 5 > 3 > 2 (группа экспертов1);

5 > 2 > 1 > 3 > 4 (группа экспертов2);

• 5 = 4 = 3 = 2 = 1 (группа экспертов3).

Ранжировки были введены нами в программу ORDEX [6]; результаты после обработки приведены в табл. 1, в которой введены обозначения:

группа экспертов 1 – a1;

группа экспертов 2 – a2;

группа экспертов 3 – a3.

Таблица 1

Результаты обработки экспертных ранжировок программой ORDEX

№	Инвесторы	Эксперты
		a 1	a 2	a 3
		Коэффициент надежности инвесторов
1	f 1 –1	0,37	0,18	0,20
2	f 2 –2	0,08	0,25	0,20
3	f 3 – 3	0,12	0,12	0,20
4	f 4 – 4	0,25	0,08	0,20
5	f 5 –5	0,18	0,37	0,20

Примечание. Сумма компонент векторов по всем столбцам табл. 1 равна 1.

Перемножив далее в каждом столбце табл. 1 коэффициенты, трактуемые как показатели надежности подрядчиков, получаем:

• f *(ai) = fiCaa^Caa^Caa^Caa^Caa =

• = 0,37 * 0,08 * 0,12 * 0,25 * 0,18 = 0,00015;

f ‘(02 ) = fi(2 )f2(a₂)f₃*(a₂)f₄*(a₂ )f^<2 ) = = 0,18 * 0,25 * 0,12 * 0,08 * 0,37 = 0,00015;

f *(0.3 ) = f i* (a₃ )f^a₃)nia₃)f:La₃ )f₅*(a₃ ) =

• = 0,20 * 0,20 * 0,20 * 0,20 * 0,20 = 0,00032;

• и эти значения переносим в табл. 1А.

Таблица 1А

Справедливый компромисс (по Гранбергу)

Показатели справедливого компромисса

0, 00015

0, 00015

0, 00032

Из табл. 1А получаем произведения, трактуемые в соответствии с [7, c. 63, формула (2.11)] как показатели справедливого компромисса. Введем коэффициенты надежности пяти подрядчиков в формат алгоритма Шепли [7] для трех групп экспертов.

Группа экспертов 1: 1 = ν (0,37)

2 = ν (0,08)

3 = ν (0,12)

4 = ν (0,25)

5 = ν (0,18)

Группа экспертов 2: 1 = ν (0,18)

2 = ν (0,25)

3 = ν (0,12)

4 = ν (0,08)

5 = ν (0,37)

Группа экспертов 3: 1 = ν (0,20)

2 = ν (0,20)

3 = ν (0,20)

4 = ν (0,20)

5 = ν (0,20)

Опустим в данной статье ход вычисления по алгоритму Шепли и сошлемся на опубликованную ранее нашу статью [8], где алгоритм решения описан для общего случая, но полностью применим в приводимом ниже расчетном примере.

Результат приведен в табл. 2 и показывает, что любая сумма государственных средств, выделенная инвестором на реализацию проекта, должна делиться между ними в пропорции, указанной в этой таблице.

Таблица 2

Расчеты по алгоритму Шепли

№	Инвесторы	Группа экспертов 1	Группа экспертов 2	Группа экспертов 3
1	П - Газпром	0,32	0,18	0,20
2	П2 - НОВАТЭК	0,11	0,24	0,20
3	П3 - Газпромнефть	0,14	0,14	0,20
4	П4 - Внешэкономбанк	0,24	0,11	0,20
5	П5 - Внешторгбанк	0,18	0,32	0,20

Таблица 2А

Справедливый компромисс (по Шепли)

Показатели справедливого компромисса

0, 00015

0, 00015

0, 00032

При сравнении табл. 1А и 2А получаем одинаковый вектор по алгоритму Шепли и по критерию справедливого компромисса, так как коалиции формировались на основе коэффициентов надежности в табл. 1.

Рассмотрим теперь случай, когда подрядчики формируют коалиции относительно известного им рейтинга надежности, данного им от групп экспертов изначально. Как показывает практика, подрядчики с более высоким рейтингом склонны взаимодействовать с другими подрядчиками, чьи рейтинги близки к их собственным. А вокруг подрядчиков с низким рейтингом образуются группы с подобным рейтингом или чуть ниже. В такой ситуации подрядчик с высоким рейтингом старается поглотить или исключить из уравнения подрядчика с низким рейтингом.

Определим вектор Шепли с помощью алгоритма, описанного М. Интрилигатором в [9, с. 181-187]. Предположим, что каждый игрок (в нашем случае подрядчик) получает выигрыш, равный средней величине своих вкладов во все те коалиции, куда он мог бы вступить. Выигрыш i-го игрока равен средней взвешенной из v (SU {i}) -v (S), где S - это любое подмножество игроков, не содержащее игрока i, a SU {i} - то же самое подмножество, включающее игрока i. Обозначим че- рез N все множество игроков, содержащее n элементов. Тогда средне взвешенный выигрыш участника i равен платежу по формуле

П'  1/ „ ( s ) [v( S U И)-v( S )],      (,)

5 c N где взвешивающие множители Yn (S) равны s!(n - s-1)!

Y n ( ^S ) =               .              (2)

n !

a s - это число игроков в S. Выбор именно таких взвешивающих множителей обусловлен следующими обстоятельствами: коалиция из n участников может быть образована различными способами; существует s! различных способов организации для s игроков, входящих в коалицию S до того, как к ней присоединяется игрок i; игроки, не входящие в расширенную коалицию, число которых равно (n - s - 1), могут быть организованы (n - s - 1)! различными способами. Следовательно, если предположить, что все n! способов формирования коалиций, состоящих из n игроков, равновероятны, то yn (S) представляет собой не что иное, как вероятность присоединения игрока i к коалиции S.

В развитие нашей гипотезы, как только инвестор с низким рейтингом вступает в коалицию с инвестором с высоким рейтингом, рейтинг инвестора с низким приравнивается к 0. Для наглядности распишем ход вычислений в группе экспертов 1.

Коалиции из 2-х участников:

v (1,2) = 0,37 + 0 = 0,37

v (1,3) = 0,37 + 0 = 0,37

v (1,4) = 0,37 + 0,25 = 0,62

v (1,5) = 0,37 + 0 = 0,37

v (2,3) = 0,08 + 0,12 = 0,21

v (2,4) = 0 + 0,25 = 0,25

v (2,5) = 0,08 + 0,18 = 0,26

v (3,4) = 0 + 0,25 = 0,28

v (3,5) = 0,12 + 0,18 = 0,30

v (4,5) = 0,25 + 0 = 0,25

Коалиции из 3-х участников:

v (1,2,3) = 0,37 + 0 + 0 = 0,37

v (1,2,4) = 0,37 + 0 + 0,25 = 0,62

v (1,2,5) = 0,37 + 0 + 0 = 0,37

v (1,3,4) = 0,37 + 0 + 0,25 = 0,62

v (1,3,5) = 0,37 + 0 + 0 = 0,37

v (1,4,5) = 0,37 + 0,25 + 0 = 0,62

v (2,3,4) = 0 + 0 + 0,25 = 0,25

v (2,3,5) = 0,08 + 0,12 + 0,18 = 0,38

v (2,4,5) = 0 + 0,25 + 0 = 0,25

v (3,4,5) = 0 + 0,25 + 0 = 0,25

Коалиции из 4-х участников:

v (1,2,3,4) = 0,37 + 0 + 0+ 0,25 = 0,62

v (1,2,3,5) = 0,37 + 0 + 0 + 0 = 0,37

v (1,3,45) = 0,37 + 0 + 0,25 + 0 = 0,62

v (1,2,4,5) = 0,37 + 0 + 0,25 + 0 = 0,62

v (2,3,4,5) = 0 + 0 + 0,25 + 0 = 0,25

Коалиция из всех участников:

v (1,2,3,4,5) = v (n) = 1.

Далее полученные результаты проанализируем в формате алгоритма Шепли для каждой группы экспертов. Все необходимые формулы для расчета можно найти в статье [8].

Результаты запишем в табл. 3.

Таблица 3

Расчеты по алгоритму Шепли

№	Инвесторы	Группа экспертов 1	Группа экспертов 2	Группа экспертов 3
1	∏1 – Газпром	0,34	0,14	0,20
2	∏2 – НОВАТЭК	0,13	0,25	0,20
3	∏3 – Газпромнефть	0,14	0,14	0,20
4	∏4 – Внешэкономбанк	0,25	0,13	0,20
5	∏5 – Внешторгбанк	0,14	0,34	0,20

Основные отличия табл. 3 от табл. 2 заключаются в том, что образовались две группы. Первая группа подрядчиков – с низким рейтингом (голубого цвета) и группа с высоким рейтингом (оранжевого цвета).

Результаты

Результатом является сопоставление справедливого компромисса по Гранбергу и компромисса по Шепли и вывод о полезности результата как в случае, когда оба компромисса совпадают, так и когда не совпадают. Обе ситуации расширяют поле для системного анализа проблемы оценки и его углубление в зависимости от целевых установок заказчика.

Практическая полезность результата для заказчика заключается в возможности принять обоснованное решение при распределении фиксированного объема инвестиций между подрядчиками. Последние, в свою очередь, при объединении в разные технологически допустимые коалиции обеспечивали бы стабильность и надежность при выполнении необходимых работ по реализации проекта.

Обсуждение результата и комментарии

Когда настоящая статья готовилась к печати, состоялось два события, заслуживающих специального комментария.

Первое. Было получено свидетельство на программу ASPER, где основным модулем является программа ORDEX (см. ссылку в начале статьи).

Получившийся комплекс ASPER (Automatic System of Process Expert Range) предназначен для выбора наиболее предпочтительного решения (альтернативы) в условиях риска и неопределённости и может применяться в управлении инвес- тиционными проектами и стратегическом планировании на этапах прединвестиционных обоснований, когда проблемы оценки и выбора являются слабо структуризованными; информационная база программы формируется группами экспертов, создаваемых пользователями программы.

Программный комплекс обеспечивает выполнение следующих функций:

• –    отображает дерево целей проблемы оценки и выбора (в иерархическом виде);

• –    обрабатывает суждения экспертов при кван-тифицикации дерева, трансформируя порядковые экспертные оценки в оценки количественные [10], [11];

• –    устанавливает приоритеты критериев в различных сценариях развития внешней среды [4];

• –    формирует оценочную (платёжную) матрицу «альтернативы – сценарии»;

• –    определяет предпочтительность альтернатив по критериям теории принятия решений [12, 13];

  – осуществляет проверку согласованности суждений экспертов [14].

Таким образом, комплекс является универсальным, т. е. применимым не только в железнодорожной отрасли.

Авторы программы: Беспалов И.А., Кибалов Е.Б., Пятаев М.В.

Второе. На недавнем Международном форуме «Один пояс, один путь» президент России В.В. Путин  ска зал следующее, относящееся непосредственно к настоящей статье [15].

«Ещё один транспортный меридиан с Севера на Юг пройдёт через Уральский регион России и Сибирь. Его ключевые элементы – это модернизация центрального участка Транссиба, включая Западно-Сибирскую железную дорогу на территории наших областей – Омской области, Новосибирской, Кемеровской, Томской областей, Алтайского края – это всё регионы Сибири России. Это также строительство Северного широтного хода (курсив наш – авт.), как мы его называем,– это ещё одна железнодорожная ветка с выходом к портам Северного Ледовитого океана и полуострова Ямал на севере российского Красноярского края – и новой Северо-Сибирской железнодорожной магистрали от Ханты-Мансийского автономного округа России до её стыковки с нашей крупнейшей железнодорожной сетью, с Транссибом и Байкало-Амурской магистралью».

Приведенная ссылка указывает не только на актуальность темы статьи, но и методологически оконтуривает ее содержание в геополитическом контексте.