Проектный метод в инженерном образовании

^w^1            eISSN 2311-2468

EDN:                                  

Проектное обучение (PBL – Project-Based Learning) [1] как дидактическая система и проектный метод как педагогическая технология1 со всеми известными достоинствами (проблемность, командность, диалогичность, интегративность, контекстность и др.) на практике доказали свою эффективность. Поскольку проектный метод является основным при реализации проектного обучения, то зачастую термины «проектное обучение» и «метод проектов» рассматриваются как тождественные [2].

Актуальными для исследования остаются практические аспекты реализации данного метода, которые в контексте инженерного образования проявляются особенно отчетливо. Это обусловлено непосредственной связью применения проектного метода с процессом проектирования как такового, который является ключевой областью профессиональной деятельности инженера и учебной дисциплиной для студентов.

Стоит отметить, что в самой постановке задач проектного метода применяются термины, характерные для научно-технической сферы, такие как конструирование, траектория, широкий перечень параметров количественного типа. Применение метода проектов в инженерном образовании обладает рядом специфических особенностей, одной из которых является возможность постановки задач метода проектов в инженерных (кибернетических) терминах, что делает понимание метода более структурированным и системным.

Цель исследования – сформулировать и реализовать задачу метода проектов в инженерных (кибернетических) терминах, что позволит систематизировать и структурировать педагогический опыт, представив его в форме, которая будет понятна и доступна для специалистов в области инженерии.

ОБЗОР ЛИТЕРАТУРЫ

Метод проектов прошел долгий путь развития в отечественной и зарубежной педагогической теории и практике с начала XX в. и до наших дней. Периодизация этапов развития метода предлагается Е. А. Пеньковских [2] и Е. А. Евстафьевой [3], где анализируется становление данного метода в отечественной и зарубежной педагогике.

• Е . А. Евстафьева обосновала актуальность метода в контексте современных требований, а в качестве требования к реализации метода рассмотрела выполнение постоянно усложняющихся практических заданий – проектов [3].

Метод проектов играет ключевую роль в развитии творческой активности обучающихся, которая проявляется на различных уровнях и в разнообразных аспектах подготовки, включая как инженерные, так и гуманитарные направления2. Ряд авторо рассмотрел теоретические и практические аспекты реализации проектного метода в вузах России [4], результаты его применения в зарубежных вузах, а также анализ критериев оценки данных результатов представлены в исследовании П. Го и других авторов [5].

Стратегия применения проектного метода на разных уровнях инженерного образования изложена в работе [6]. Важной особенностью метода в инженерном образовании является его интегрируемость с аналогичными подходами на стадии школьного обучения, в частности, опирающимися на методологию STEM (Science, Technology, Engineering,

• ²    Козлова Л. С., Каюпова А. С., Мамлеев Д. Р. Проектный метод обучения как дидактическое средство развития творческой активности учащихся // Педагогическая наука и образование в диалоге со временем : сб. материалов IX Междунар. науч.-практ. конф., посвященной памяти В. А. Пятина (14 июня 2024 г., г. Астрахань). Астрахань : Астраханский государственный университет им. В.Н. Татищева, 2024. С. 54–58.

Mathematics) [7]. Интерес представляет собой кибернетический подход к постановке и решению образовательных задач [8; 9], который в части интеграции его с методом проектов имеет, с нашей точки зрения, особенно благоприятные перспективы.

МАТЕРИАЛЫ И МЕТОДЫ

Рассмотрим двумерное сечение (x_i,x_i),j = й гиперпространства размерности n , которое будем называть пространством компетенций. Каждое координатное направление представляет собой действительную числовую ось, вдоль которой сгруппированы и соотнесены с числовыми значениями некоторые компетенции, следующие в порядке усложнения и соответствующие одной или нескольким учебным дисциплинам (модулям). Одна из таких координатных осей x_i частично конкретизирована нами в контексте важной в инженерном образовании общетехнической дисциплины – сопротивления материалов. Числовые значения (координаты), соответствующие точкам на координатных осях, в дальнейшем для краткости будем называть значениями компетенции.

Абитуриент, поступающий в вуз, характеризуется начальной точкой в этом пространстве, принадлежащей начальному гиперпараллелепипеду (или подобласти другой формы) весьма ограниченного объема и находящемуся в непосредственной близости от начала отсчета. Факт принадлежности этой начальной точки указанному гиперпараллелепипеду является критерием того, что данный человек является абитуриентом.

В процессе обучения в статусе студента обучающийся совершает движение в данном пространстве по некоторой траектории из начальной^точки (№ - ее координатный вектор) и достигает в итоге некоторой целевой точки ( x - ее координатный вектор), которая принадлежит целевой подобласти в этом пространстве – гораздо более значительных размеров, чем начальная подобласть – и является удаленной от начала отсчета на гораздо более значительное расстояние. Факт принадлежности конечной точки этой целевой подобласти является критерием того, что обучающийся приобрел квалификацию «инженер».

Задача кибернетики ставится следующим образом: задать управление (воздействие) на систему, обеспечивающее на заданном периоде времени движение начальных точек по траекториям, конечными точками которых являются целевые точки, принадлежащие целевой области.

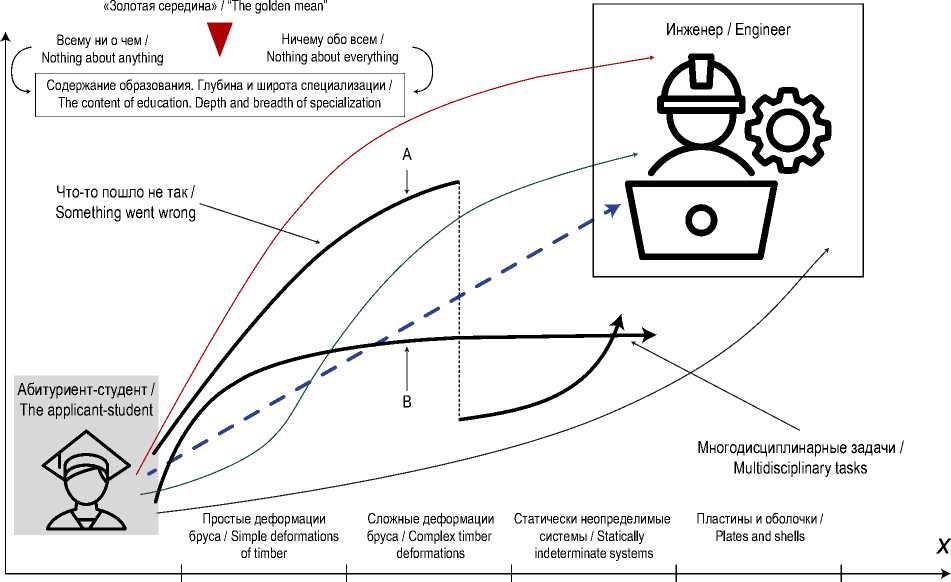
Качественный анализ траекторий, т. е. функций, графики которых представлены на рисунке 1, позволяет сделать следующий очевидный вывод: эти функции должны быть гладкими.

Обеспечить гладкость функций и реализацию рассматриваемой модели в целом позволит выбор конкретных задач проектирования, которые выбираются в качестве базовых для реализации проектного метода. Этот вопрос, с нашей точки зрения, является ключевым и существенным образом влияет на результаты образовательного процесса. Для успешного выполнения поставленных задач необходимо соблюдение следующих ключевых критериев: актуальность (востребованность) и представленность в медиапространстве, наукоемкость, комплексность и междисциплинарность.

100                        200                        300                        400                       500

Р и с . 1 . Индивидуальные образовательные траектории в пространстве компетенций

F i g . 1 . Individual educational paths in the competence space

Источник: здесь и далее рисунки составлены авторами.

Source: here and further, the drawings are compiled by the authors.

Примечание: пунктирный вектор – направление подготовки; кривые красного и зеленого цветов – допустимые индивидуальные траектории, относящиеся к категории успешных; A, B – траектории, не приведшие к желаемому результату.

Note: The vector shown in dotted lines represents the direction of learning; the red and green curves represent the acceptable individual trajectories that are considered successful; A and B represent the trajectories that did not lead to the desired outcome.

Первые три критерия не требуют дополнительных комментариев. В отношении четвертого критерия, «междисциплинарность», следует отметить, что задача должна быть именно междисциплинарной, а не многодисциплинарной, т. е. обладать множеством всесторонних междисциплинарных связей. В противном случае (в случае многодисциплинарного подхода) образовательные траектории будут представлять собой составные кривые, включающие прямолинейные звенья, параллельные координатным осям, либо содержащие разрывы.

Индивидуальность каждой траектории определяется личностными особенностями студента и его специализацией как разработчика ( Maker ) и пользователя ( User ), поиском той «золотой середины» в глубине и широте специализации, между двумя полюсами («всему ни о чем» и «ничему обо всем»). На основании нашего педагогического опыта мы можем наблюдать наличие у студентов склонности к одному из двух видов указанной деятельности либо к обоим одновременно (рис. 1).

Индивидуальные особенности студента могут быть формализованы с использованием квадратичных функций (кривых второго порядка) F (α, β), заданных в координатах α и β (рис. 2), где α характеризует широту специализации студента, β – характеризует глубину специализации.

Поясним физический смысл переменных α и β на конкретном примере. В данном проекте особую роль играют цифровые технологии, связанные с автоматизированным проектированием (CAx-моделированием), а также с решением задач по разработке CAx-систем, обусловленных необходимостью расширения и углубления их штатного функционала. Моделирование (описание) объекта проектирования выполняется в разных аспектах: конструкторском, технологическом, функциональном. Функциональный аспект предусматривает описание объекта многоаспектным образом в терминах механики, электроники, гидравлики и проч. Кроме того, это описание для каждого аспекта может быть выполнено на разных уровнях сложности: деталь-сборка, линейность-нелинейность, статика-динамика и т. д. Таким образом, переменная α характеризует многоаспектность задачи, а переменная β – ее сложность. Заметим, что многоаспектность описания модели напрямую связана с междисциплинарностью задачи проектирования.

В рамках настоящего проекта планируется решение задачи разработки как в пределах заданного спектра многоаспектности, так и на определенном уровне сложности.

Например: «Разработать StandAlone API-приложение на базе COM для решения задачи траекторного управления мобильным роботом»3.

Функция F (α, β)⁴ имеет вид:

F(α, β)=a11α2+ 2a12αβ + a22β2+2a1α + 2a2β + a0, где a0, a1, a11, a12, a22– коэффициенты.

Таким образом, различные сочетания значений коэффициентов в формуле позволяют описать все возможные подходы к построению индивидуальных образовательных траекторий. Графиками этих функций являются конические сечения (коники) на плоскости (α, β), которую в дальнейшем будем называть плоскостью специализации. На рисунке 2 представлены по одной кривой из каждого семейства: эллипсов, парабол и гипербол с совпадающими фокусами (за исключением частных случаев).

Наша задача – провести качественный анализ этих функций при движении некоторой текущей точки от одного фокуса эллипса ( O ₁) до другого ( O ₂). Это наиболее часто встречающийся на практике случай.

Первая координатная четверть делится на две части биссектрисой на две полуплоскости. Верхняя часть характерна для разработчиков и соответствует более углубленной, но узкой специализации. Нижняя полуплоскость характерна для пользователей с менее углубленной подготовкой, но с более широкой специализацией.

Для любой текущей точки глубина специализации разработчика определяется длиной перпендикуляра от точки до биссектрисы, если точка лежит в верхней полуплоскости. Аналогичным образом определяется глубина специализации пользователя, если точка принадлежит нижней полуплоскости. Соответствующие утолщенные отрезки синего цвета показаны для случая эллипса (рис. 2).

Эллипс иллюстрирует следующее: при расширении специализации (многоаспект-ности), т. е. при увеличении α глубина специализации разработчика снижается (движение от точки 1 до точки 2 ); глубина специализации пользователя наоборот возрастает (движение от точки 3 до точки 4 ). Эта кривая соответствует студентам, которые проявляют на данном интервале склонность и к деятельности пользователя, и к деятельности разработчика одновременно. Однако, чтобы добиться оптимума нужно быть внимательным с многоаспектностью. Таких студентов, как правило, большинство (до 80 %).

Гипербола представляет прежде всего теоретический интерес и соответствует варианту, когда студент проявляет склонность лишь к одному из видов деятельности: либо пользователя, либо разработчика, т. е. функция однозначна. Более того, гипербола имеет две асимптоты в виде координатных осей, именно они соответствуют двум теоретически возможным предельным состояниям «всему ни о чем» и «ничему обо всем», здесь речь идет о сложности задачи, характеризуемой переменной β. На практике при движении на заданном интервале этой кривой соответствуют самые слабые студенты (10–15 %), которые не усваивают компетенции разработчика, а компетенции пользователя осваивают на простейших задачах.

Парабола на практике встречается редко (не более 5 %). Это наиболее способные студенты. При движении на заданном интервале кривая иллюстрирует склонность студента как к деятельности пользователя, так и к деятельности разработчика, причем глубина специализации только возрастает с увеличением многоаспектности и по первому, и по второму критериям.

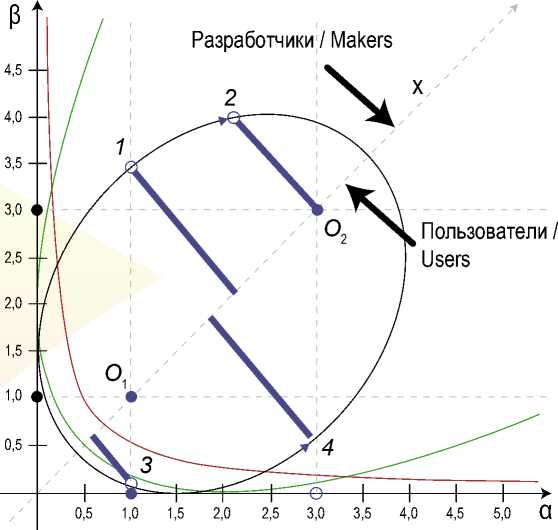
Р и с . 2 . Плоскость специализации: 1 – начальная точка, соответствующая разработчику; 2 – конечная точка, соответствующая разработчику; 3 – начальная точка, соответствующая пользователю; 4 – конечная точка, соответствующая пользователю

F i g . 2 . Individual educational path in the competence space: 1 – the starting point corresponding to the maker; 2 – the finish point corresponding to the maker; 3 – the starting point corresponding to the user; 4 – the finish point corresponding to the user

Примечание: O ₁, O ₂ – фокусы эллипса.

Note: O ₁, O ₂ – ellipse focuses.

Принимая во внимание всю совокупность трудностей, связанных с практической реализацией задач в области киберпедагогики [9; 10], мы не намерены предлагать данную модель для непосредственной практической реализации с использованием конкретных численных параметров. Данная модель предназначена для более полного качественного понимания содержательных аспектов проектного метода, а также для уточнения смысла некоторых терминов, таких как «индивидуальная образовательная траектория» [10].

В результате многочисленных проб и ошибок мы остановили свой выбор на следующей задаче проектирования: «На предложенной программно-аппаратной базе разработать интегрированную модель мобильного робота или прототип электромобиля, включающего в себя три составляющие: а) виртуальную CAx-модель, т. е. собственно проект; б) натурную модель; в) единую систему управления движением, включая автономное поведение» [11].

На рисунке 3 показана натурная и виртуальная модель колесного робота на одной из используемых нами платформ (KuGoo).

Р и с . 3 . Интегрированные модели: а) натурная модель; б) виртуальная модель: 1 – механические передачи, рулевое управление; 2 – система управления, радиосвязь, телеметрия, очувствление (сенсорика); 3 – технологический модуль; 4 – движители; 5 – энергообеспечение

F i g . 3 . Integrated models: a) full-scale model; b) virtual model: 1 – mechanical transmission, steering; 2 – control system, radio communication, telemetry, sensing; 3 – technology module; 4 – thrusters; 5 – energy supply

Дисциплины (модули), обеспечивающие компетенции, необходимые для реализации данного проекта:

• 1.    Физико-математические науки.

• 2.    Механика (как раздел физики, теоретическая механика, механика деформируемого твердого тела).

• 3.    Электроника и схемотехника.

• 4.    Автоматическое управление.

• 5.    Автоматизированное проектирование (CAD/CAE).

• 6.    Информатика и программирование.

• 7.    Натурное моделирование и экспериментирование.

• 8.    Технологии высокоточных измерений, прототипирования, механической обработки.

Особого внимания к себе, на наш взгляд, заслуживают компетенции из области информатики и программирования. Процесс программирования всегда более интересен, легче верифицируется и тестируется, если он связан с компьютерной графи- кой. Более того, дисциплины, связанные с автоматизированным проектированием, которые полностью реализуются «на экране компьютера», гораздо более интересны для студента, если предусматривают то или иное материальное воплощение объекта проектирования.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

Разработан модельный ряд для интегрированных (натурных и виртуальных) моделей на различных платформах: KuGoo, Injora, BigoLand, а также методические материалы в виде онлайн-курса на базе Moodle, включающего в себя SCORM-пакеты и другие структурированные полнотекстовые материалы с мультимедийным контентом. Основные результаты в части построения интегрированных моделей, используемых в данном проекте, иллюстрируются следующими видеоматериалами:

• 1 ) решение задач траекторного управления и путевой стабилизации, разработка виртуальных, натурных и интегрированных моделей на базе KuGoo⁵;

• 2 ) реализация технологий прототипирования⁶;

• 3 ) тестирование виртуальных и натурных моделей на базе BigoLand⁷;

• 4 ) онлайн-курс⁸.

Авторы не проводили статистических наблюдений и исследований, однако зафиксировали явные позитивные качественные изменения по следующим параметрам: управляемость, воспроизводимость, индивидуализация и дифференциация, инновационность, а также по показателям, связанным с активностью, мотивацией и креативным потенциалом студентов.

ОБСУЖДЕНИЕ И ЗАКЛЮЧЕНИЕ

В ходе исследования полностью подтверждена эффективность проектного метода, которая обеспечена выбором задачи проектирования. Подтверждается высказанная гипотеза о необходимости материального воплощения абстрактных моделей проектирования. Это качественным образом повышает интерес студентов к объекту проектирования, приближает проект к реальности.

В процессе реализации проекта решаются междисциплинарные задачи, завершающиеся проведением тест-драйва спроектированного, собранного и запрограммированного студентами робота, т. е. состояние и поведение объекта проектирования не только созерцается студентами за счет применения средств компьютерной графики, но и осязается ими как реальный материальный объект.

Опыт авторов, представленный в данной статье, может быть легко адаптирован для других задач проектирования, но непременно являющихся при этом наукоемкими и междисциплинарными.

• ⁵    TrajectoryControlDigitalTwins [Электронный ресурс] // Rutube : видеохостинг. URL: https://rutube.ru/video/private /611887da547c7e3b28232963e54ffead/?p=GDqEfxgehR4c4h61S37sPw (дата обращения: 05.06.2025).

• ⁶   Technology [Электронный ресурс] //   Rutube   :   видеохостинг.   URL:   https://rutube.ru/video/

  private/8fde127a1b7d1546002b27830f53ed24/?p=j2CbIlKRR74bWCjmnjOthA (дата обращения: 05.06.2025).

• ⁷   BigoLand [Электронный ресурс] //   Rutube   :   видеохостинг.   URL:   https://rutube.ru/video/

  private/9865d72b8ee7a08e18a80182fc8bf913/?p=rY4EXiP45SZHw0iQRxUT_A (дата обращения: 05.06.2025).

• ⁸    OnLineCourse [Электронный ресурс] // Rutube : видеохостинг. URL: https://rutube.ru/video/private/5e8a17e6210 efce8f4a2e611d1e11c93/?p=qYxROQioB_vc7M_k5V3imw (дата обращения: 05.06.2025).

Pedagogical sciences                                                          285