Программный комплекс для работы с матрицами Дирака Susy_Diracus

В современной теоретической физике вычисления с привлечением аппарата клиффордовых алгебр ведутся в широких масштабах. Благодаря трудам таких авторитетных и опытных специалистов в области компьютерной алгебры как В.А. Ростовцев, уже в 70-х годах прошлого столетия для подобных работ стали появляться автоматизированные комплексы [ 1] .

В современных работах часто приходиться иметь дело с выражениями, состоящими из объектов разной математической природы таких как: комплексные числа, элементы различных алгебр, элементы векторных и тензорных пространств над такими алгебрами. Например: в [2] на функции f = XX ai，ii...ik YY((Y Ү lq) C T)     Өа0 ...Өап Өв0 ...Өвп             ⑴

• k li…lk         n=0 \ \q=1    /      / _anen

• ¹    E-mail: miklul@rambler.ru

где а* 、… ik — фуикции от x^a, a = 0 ... 3, Ө^аӨ^в + Ө^вӨ^а = 0 (образующие алгебры Грассмана), (ү^а) ； — гам ма-матрицы Дирака и

C = іү 0ү2

действуют операторы вида:

Mab = Xadb - Xbda +! 9以Y。心0 ； что приводит к громоздким выражениям. В вычислении метрики суперпространства де Ситтера используется супердифференциальный оператор [2]

Ko = 2x0X^bdb - x²do + (xa (үоү^а ) І Ө " - 3 】〃 ү (ү⁰)Т Ө " Ө 〃 Ө^ү) дт+

+ \(C"vg (Ү0ҮЬС-1)тп +(Y0Y5C-1)п"(Y5YbCT)vg -(Y0Y5CT)ng(Y5YbC一') v" + +(Y0Y5C-1)nv(Y5YbC-1)g" )ӨПӨ"ӨvӨ«дь что приводит к выражениям, содержащим несколько тысяч слагаемых. Несмотря на обилие компьютерных средств, выбрать инструмент для подобных задач непросто. Однако системы компьютерной алгебры постоянно совершенствуются. Прекрасно зарекоммендовала себя система Саdabra [3]. Однако ей пока далеко до мощи Wolfram Mathematica и Maples о ft Maple. Необходимость решения описанных выше задач суперматематики привела к созданию комплекса SUSY_Diracus. Наш комплекс построен на базе системы Maple 2016 и успешно работает в более новых версиях. В отличие от проекта [4, 5], здесь есть возможность реализации работы в алгебре Клиффорда с произвольной сигнатурой. В данном случае комплекс настроен на лоренцеву сигнатуру +----.

Реализован механизм сверток по немым спинорным индексам. Терминология комплекса совпадает с терминологией, принятой в работах [2] , [6] , что делает его особенно привлекательным для изучения супермногообразий. Если рассмотреть недавно появившийся пакет GammaMaP для Wolfram Mathematica [7] , можно заметить, что в нем отсутствуют инструменты работы с представлением ү-матріш, в лііііеппом пространстве. Но в задачах подобных решаемым в [2] в тшх во ： зипкает серьезная необходимость. Здесь эти функции реализованы в полной мере и весьма остроумно (7.10). В отличии от пакета GammaMaP мы написали расширение функции diff (8.1) на суперслучай, можно видеть, что комплекс с такими возможностями представлен впервые и хорошо подходит на роль производственной базы для ^пиндустриального метода написания суперсимметричных лагранжианов..." [8] , опираясь на фундаментальные симметрии [9] физических систем. Благодаря таким инструментам, к громоздким вычислениям можно приступать с большей уверенностью [10] .

Мы надеемся, что наша работа продолжит направление [1] , [11] . Комплекс состоит из сорока четырёх процедур выстроенных по принципу многоуровневой обработки данных (рис. 1) .

Для работы с нашим комплексом его нужно подключить:

Необходимые для работы файлы доступны по адресу: Загрузите всё в один каталог, откройте и начните работать. Вы можете сохранить вашу работу под любым именем.

1.    Постановка задачи

Пусть задано математическое выражение, включающее в себя матрицы Дирака (ү 。 ) ：， например, вида ( I) . Чтобы упростить такое выражение, требуется произвести соответствующие свертки и коммутации.

Для рассмотрения этой задачи, необходимо описать полный граф состояний вычислительного процесса. Ограничимся вычислением многочлена, слагаемыми которого служат произведения многочленов. В этом случае вычисление начинается с алгебраических действий, т.е. с раскрытия скобок и т.д. В полученном многочлене анализируется каждый моном на предмет возможности сверток. Сами свертки нужно провести в соответствии с порядком индексов, а затем выполнить необходимые коммутации гамма-матриц. Каждый пункт определяет уровень обработки выражения.

Основной возможностью, позволившей нам быстро реализовать алгоритм работы с матрицами Дирака, стала способность среды Maple создавать алгебраические объекты неалгебраическими методами.

Прежде чем реализовать алгоритм, нужно разобраться в способностях исполнителя. В нашем случае исполнителем будет среда Maple 2016. Сначала мы приведем краткие описания двух встроенных функций, позволивших нам реализовать свой алгоритм.

2.    Subs

Subs команда подстановки подвыражения в выражение.

subs(x=a,expr)

subs([Sl,...,Sn],expr)

subs [inplace] (x=a,expr)

subs[inplace]([Sl,..., Sn], expr)

Первая форма команды подстановки subs заменяет x на a в выражении expr. Следует отметить, что эта команда аналогична команде Eval. Простые операции из ряда замен символа на его значение в формуле, как правило, следует сделать с помощью команды Eval. Различия между этими двумя командами в том, что при работе с Eval старая переменная остается связанной в данном выражении.

Вторая общая форма команды подстановки subs делает замены указанные первом аргументе в expr. Каждый из S1,…,SN представляет из себя равенство х, = а, или список равенств заключенные в фигурные или квадратные скобки. Замены выполняются последовательно, начиная с S1. Замены в рамках списка выполняются одновременно; если есть несколько замен на то же имя, используется первый.

Параметр Inplace применяется только при замене в expr типа rtable (таких как Array, Matrix, или Vector), без функции индексации. Когда Inplace указан, вход rtable обновляется на месте. В этом случае меняется именно оригинальное выражение expr, а не создаётся его копия. Действие замены не включает упрощение выражения. В тех случаях, когда желательно упростить выражение, следует использовать команду Eval.

3.    Описание функции ор op(i, e)

op(i..j, e)

op(e)

op(list, e)

nops(e)

Функция op раскладывает выражения на составные части. Прелесть этой ( ] ) ункп,ші в том ii состоит, что в результате мы получаем набор деталей исходного выражения, которыми в дальнейшем можно свободно манипулировать. Начнем с того, что для некоторых структур данных определена опция op(0,e). Эта опция открывает колоссальные возможности для программирования в Maple. В таблице ниже приведены результаты применения op к выражениям разных типов и конструкций. Так для функций, op(0, e) возвращает имя фуикции. Для индексных имен, op(0, e) это имя без ндексов.

Конструкция выражения е	op (е)	0P (0, е)
Адитивность a + b,    a — b	a, b	屮
Мультивность a ∗ b,       a b	a, b	‘ • ‘
ab	a, b
a = b	a, b	=
f(a,...,c)	a, . . . , c	f
ab,...,n	b, . . . , n	a
f (x) dx	f(x),x	diff
f f (x) dx	f ( x ) , x	int
a	a	symbol

Выражение e в контексте ( 1 ) упктпш op представляет собой объект, состояттпіп из членов (операндов )е. связанных ^знаками математических оператпіп. которые в соответствиями со своими приоритетами задают уровни вложенности.

В простейшем случае функция op возвращает список частей е, связанных наимение приоритетной операцией. Так если op имеет только один аргумент, она возваратит результаты, представленные во 2-м столбце таблицы. Это равносильно вызову, op(1..nops(e), е). Если первый аргумент в op список, то элементы списка относятся к операндам е с во ： зра ， статотп,іпш уровнями вложешюстп. Это просто краткая форма записи. Выражение op([A1,A2,..., ],е) возвращает тот же результат, что ii op(An,op(...,op(A2,op(A1,e))...)) но является более быстрым для выполнения. Когда, первый параметр представляет собой список, последний элемент списка может быть интервалом. Как говорилось выше, это всего лишь краткая форма записи. Выражение op([A1,A2,...,an1..an2],e) возвращает тот же результат, что и op(an1..an2,op(...,op(A2,op(A1,e))...)), но является более эффективным для выполнения.

nops — (функция во ： звра ， ш,а ， ет количество таких дета/еіі пли операндов в выражении. Если первый аргумент функции op целое положительное число i, то возвращается i-й операнд е. Если операнд не существует, возникает ошибка. Если первый аргумент в op является отрицательным тіелым числом i то в резупьнате во^звратттается ： op(nops (е) + i + 1,е).

Для рядов. op(0, е) является x — переменная ра ： зложепия ряда ， . Вычисление op(0, series(exp(x), x = a)). возвра ， ш,а ， ет x. а не a. Для всех других структур данных. op(0, е) во ： звра ， Е,а ， ет само е. Если значения операндов селекторов не в диапазоне -nops (е) т.е. [—1...nops(e)], возникает ошибка. Если первый аргумент в op является интервалом целых чисел от i-го до j-rо [i..j], то результат представляет собой последовательность i-ro до j-ro членов е. Отрицательные целые числа в диапазоне рассматриваются, как описано выше; к ним добавляется nops(e) - 1.

4.    Способ представления произведений гамма—матриц

Нам нужно записать выражения вида:

X Ai П bam¹ ү am²

γaimi

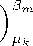
θµk

k

Поскольку выражение в скобках имеет индексы, естественно его записать конструкцией имя-индекс. Здесь вместо имени должно стоять выражение. В свою очередь выражение должно сохранять порядок множителей. Для решения этого вопроса естественно было бы полагать реализацию в виде:

• Строки,

• •    Вектор-матрицы,

• •    Множества,

• •    Полиарной функции.

5.    Принципы построения системы SUSY_Diracus

Со строками сложно работать, вектор-матрицы оказались неупотребительны системой в данной роли, множества не сохраняют порядок. Четвертый вариант в сочетании с командой ор оказался неожиданно элегантным решением. Такой функции было дано имя Q. В такой записи выражения принимают вид:

X Ai Y q Sam 】 Yam ? ... Yam ， ) ^em Y ө^ µk im          k

В основу построения нашей системы положены принципы объектно-ориентированного программирования [12, 13] , которые в нашем случае выражаются в специализации функций, что в свою очередь порождает структуру уровней рис. 1 (закрашенные поля). Это значит, что каждая из задач, представленных на уровне интерфейса, решаются не одной отдельной функцией, а группой или конвейером функций, которые вызывают одна другую как представлено на рис. 1. Интерфейсные функции принимают в качестве аргументов выражения полиномиального вида и непосредственно сами представляют собой обычные циклы суммирования результатов обработки мономов, которые доставляются функциями уровня одночленов. На уровне одночленов решаются вопросы привлечения сил клиффордова уровня и т.д.

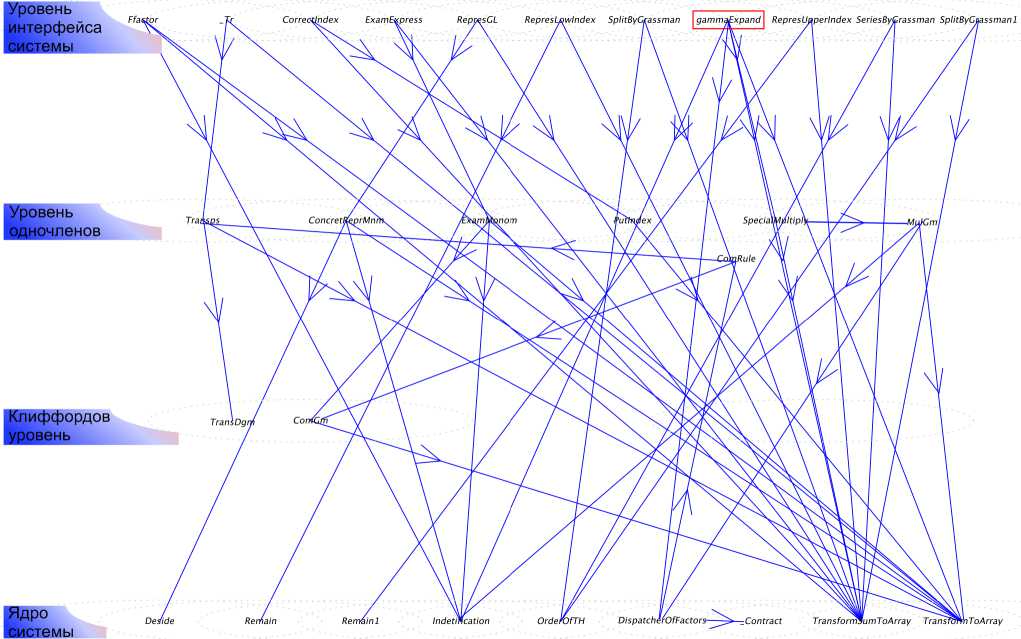
Уровень интерфейса системы

Ядро Іһістемы

Уровень одночленов

Клиффордов уровень

Рис. 1. Граф вызовов.

Согласно сказанному выше сложилась и архитектура программного комплекса. Такая архитектура позволяет легко масштабировать систему и быстро адаптировать её для других алгебр Клиффорда. В нижней строке перечислены функции, представляющие ядро системы. О них будет рассказано в конце. О функциях в других строках будет рассказано в соответствующих разделах. Впрочем, об их назначениях несложно догадаться по их именам.

6.    Общие правила и соглашения

При работе с пакетом SUSY_Diracus необходимо принять несколько соглашений.

Есть несколько символов, которые не нужно использовать в качестве переменных. Они обрабатываются функциями пакета специальным образом. Это: О,ү,8,С,С 1,пп,Ө.

• •    ү — обо ： зиачает гамма-матріш.у Дирака ү⁰,ү1,ү², ү³, ү5 ，

• •    Ө — Грассманова переменная

• •    S — символ Кроиеккера.

• •     C1 — обо ： зиа.чает іү⁰ү².

• •    C1 = C^-1 — обо ： зиачает іү²ү0.

• •    Q — имя (формальной (функции. о ( ] ) орм, 「 ятош,еіі произведение ү^а1...үan. ііапример. П(үі, үз).

• •    ПП — тензор Минковского.

• 7.    Интерфейс

  7.1.    gammaExpand

Эти символы не должны встречаться на позициях индексов и более ни в какой другой роли. Все бозонные и спинорные индексы при координатных переменных считаются верхними. В выражениях Maple:

[> xa, Өс, S£,n，Q(Tb)a,e индексы а,Ь,с,в 口 П (/штатотся верхними, a ii ^ ііііжішміі. Индексы a ii b назові^і 6<>-уні；іім,лііі. а а,в,П,£ 11 c -спинорного типа ііліі спиіюрішлш в соответствии с местом их расположения. Это выражение эквивалентно следующей математической записи [2,14,15]:

x^a,ө^c,sn, ( Y^b ) a

Обозначения Q ( Y5)a,e — есть ( Y5 ) g, т.е. в выражениях Q(...) , S…,…первый индекс считается нижним, второй — верхним. Исключение: Q(C 1)a,e - (C^-1) @户 ， Q(C ) a e - C“" Если в выражении произведения встречаются повторяющиеся индексы спинорного типа, по ним предпологается суммирование.

gammaExpand (A)

Протіедура gammaExpand — главная коммаида программного пакета комплекса. Она раскрывает все скобки и выполняет все свёртки спинорных индексов при ү^а. Ответ формулируется в терминах S, ү⁰, ү 1, ү²,ү3. В каждом мономе гамма-матріш.ы выстранватотся в порядке во ： зра ， ста ， тшя их бозонных индексов. Спинорные индексы расставляются в лексографическом порядке.

Примеры:

[> gammaExpand 。* О(ү°, үз)р,,т * Q(C)t,£ ) ；

I Q(Y2 ,үз—

Полная обработка исходного выражения осуществляется таким алгоритмом:

• ¹С помощью антисимметричной матрицы C = С^ав можно поднимать спинорные индексы а,в, ... , а с помощью обратной к ней матрицы C^-1 = C^-1_ав опускать -, согласно формулам ( [2] стр.79):

Ө^а = Өв C 旣 Өа = ( C-1 ) ваӨ^в = - ( C^-1 ) авӨ^в ■

[> S ： =...:

[> S := SimplifyByTh(expand(S)):

[> S := CorrectIndex ( S, [^1,^2,^3, ^4]) : ] если только этих индексов нет в исходном выражении.

[> S := gammaExpand(S):

[> S := ExamExpress(S):

[> S := LikeGammaMember(expand(S)):

[> S := gammaExpand(S):

Эти команды рекоммендуется оканчивать двоеточием, чтобы не загружать рабочее поле промежуточными вычислениями.

7.2.    Correctlndex

CorrectIndex (A, w)

Протіедура CorrectIndex заменяет спшюрные индексы в полиноме A. w — это множество символов, не фигуриружщих в качестве связанных переменных в скрипте и (важно) невстреча-ющихс я2 в вырыжении A.

7.3.    LikegammaMember

LikegammaM ember (A)

В выражении могут встречаться одинаковые по смыслу члены, (отличающиеся лишь немыми индексами). Так как Maple трактует их как набор символов, он не распознаёт их как подобные. Для решения этого вопроса была разработана процедура LikegammaMember, которая выявляет подобные Гамма-члены, делая соответствующие замены индексов. ВНИМАНИЕ: индексы исходного выражения не должны содержать символа ” J, т.к этот символ используется самой функцией LikegammaMember (A). Это условие всегда ， можно выполнить. 口 спо, 「 ь ： зуя ( } ) упктппо subs (см. выше). Особенностью алгоритма этой функции является обратный ход логики. Все остальные функции обратывают многочлены, обрабатывая каждый одночлен. Сдесь же работы начинается с осмотра всего иходного многочлена.

Идея алгоритма основывается на создании хеш а3 или словаря произведений ү-матриц. Это реализуется с помощью системы конструкций hashmset : -new и array.

Например: выражение

[> ^(ҮОіҮз)""% + О(Ү0, Үз)а,тӨа останется без изменений тогда как:

[> LikegammaMember (-(70,73)5 。 丛 + 0(үо,Үз)_а , _т 。 @) ；

2^(ү0,ү3)^112,т Ө^112

.Поэтому лучше:

[> CorrectIndex (LikegammaMember (-(70,73)5 。 丛 + -(үо,Үз)_а , _тӨ@) , [ 〃, т ]) ;

2-(үо,үз)"т Өн

7.4.    SimplifyByTh

Simplif yByT h (A)

Процедура SimplifyByTh убирает из выражения члены содержащие (порядок по Өа) > Dim.

7.5.    Ffactor

Ffactor (A)

Эта функция выносит общий множитель за скобки. Стандартная функция factor, к сожалению, не справляется с выражениями нашего вида.

Примеры:

• [> Ffactor( - 2 * I * к * t * П(үі,ү2,С 1) @屮 * CQ2 * CQ1 - 2 * I * к * y * О(ү°,үі,С 1) @屮 * CQ2 * CQ1 + 2 * I * x * Q(yo,Y2,C 1)a 屮 * к * CQ2 * CQ1 — 2 * к * z * О(ү5,С 1)a 屮 * CQ2 * CQ1);

• 7.6.    Вертикальное перемещение спинорных индексов.

2 * I * CQ2 * CQ1 * (I * z * Q(Y5,C 1)a 屮- t * O(Y1,Y2,C 1)a 屮 + x * O(Y0,Y2,C 1)a 屮- У * О(Ү0,Үі,С 1)a 屮)* к

RepresLowIndex и RepresUpperlndex

RepresLowIndex (A, w)

RepresUpperIndex (A, w)

Возмем произвольную гамма-матрицу (ү 。 ) ：. Мы видим два спинорных индекса — верхний и нижний. Умножим эту матрицу на ( C )迎 ( C^-1 )印 справа.

Da9 严 9^-% = 上 ке ⁰ү² ) а ( e ^- 1 爲 = 咕可)貝們 ? ( c ^- 九 =

= і ( Ү²Ү⁰Ү^а ) в ( с^-” =《 ү 2ү0ү a ) T ) в ( с^-” = і”ү⁰ү ^a ) ^Tc ^{- 1} ) _e“

Сам объект не изменился, но обрел запись с двумя нижними спинорнымми индексами. Аналогично получается запись с верхними индексами. Этот эффект можно назвать дизайном вида выражения.

Функции RepresLowIndex ii RepresUpperIndex преобразуют датшуто ^запись в ^запись с опущенными (поднятыми) индексами. Индексы, подлежащие перемещению, должны быть указаны во втором аргументе w как множества.

Примеры:

[> RepresUpperIndex(Q(Yi,Y2)a,b * 一 (үо,үз)ь,с * О(үі,үз)и@ { a,d,u } );

[> RepresLowIndex(gammaExpand(Q(Yi,Y2)a,b * О(үо,үз)ь,с * О(үі,үз)с&), { a,d } )

O(C,Y5)u,dIQ(C 1)a,d

7.7.    SeriesByGrassman

SeriesByGrassman (A)

Эту и две поел едущие функции также можно отнести к области дизайна выражений. Функция SeriesByGrassman принимает грассманово выражение ii группирует в нём слагаемые по степеням грассмановых переменных.

Примеры:

• [> SeriesByGrassman(G(x,y)+Q(Yi,Y2)a,b * Ө。+—(үо,үз)ь,с *—(үі,үз)и&* Өь *。乜―О(үі)&,ь * Ө。);

7.8.    SplitByGrassman 7.9.    SplitByGrassmanl 7.10.    RepresGL

G(x,y) + (-(үі,Ү2)а,ь ― ^(үі)а,ь) * Ө 。 + 一 (үо,үз)ь,с * О(үі,үз)и,а * Өь * Өи

SplitByGrassman (A)

Функция SplitByGrassman принимает грассманово выражение ii выдает массив, элементами которого являются однородные по степеням грассмановых переменных части исходного выражения. Так в 1-м элементе массива окажется часть выражения, не содержащая грассмановых переменных. В n-м элементе будут находиться слагаемые, иметоттпю порядок n — 1 по грассмановым переменным.

SplitByGrassmanl (A)

Это скоростная модификация предыдущей функции. SplitByGrassmanl не занимается вынесением за скобки общих множителей.

RepresGL (A, Six)

Функция RepresGL вычисляет 6£(4)-представление выражения A. Она принимает два аргумента. Первый — само выражение, второй Six-set 。/ indexes — массив его свободных индексов (записывается в квадратных скобках — [], [ а ], [ а,в ])・

Выражение не должно содержать термины C, C1 и 75.

Примеры:

[> eval (RepresGL (О(үі)а,ь, [a, b]));

• -0  0   0    -1

0  0  -10

0 100

• —1   0   00

• 7.11.    Некоторые нетривиальные примеры

  7.11.1    Пример 1

Вот пример исследования известного [2] тождества:

( ^С-'в (Ү5)ү' + С-%, (Ү5— + ( ^C-'a ^в + ( Ү5^c-1 ) ав ^ + ( 75°-%,^ +

+ (Y5c -1 ) үа 碓 =⁰ ：

[ > IC (a, b, С, d) ： = Q (Ү5, C1 )b,c Sa,d + Q(Y5, C1 )c,a ®d + —Y5, C1 )a,b'd + ■( C1 )a,b 。院 )^ + Q(C1 )b,c Q(Y5)a,d + Q(C1 )c,a 。院九 , ：

• > RepresLowIndex CorrectIndex gammaExpand LikeGammaMember gammaExpand

7.11.2    Пример 2

IC (a, b, c, d) ӨаӨьӨс ))) ,ав€ ) , {а,Ь,в,^} ⁾ ；

- 3 ӨаӨвӨ _€ ( 5a,dfi (Ү5, C1 ) _€ ,в + Q( C1 )g,e Q (Y5)a,d )

[ > A ： = ^{iC1 Q(}Y0^,Yl^,Y3⁾e,n8 ^Q ( Y0 ， Y2 ) a,v8 ^ӨП80V8 + i ^{C1 Q(}Y0,Yl ,Ү3 ) в,п8 ^Q(Y0^,Y2⁾a,_M8 ^Өп8^Ө"8 +

2 C2 Q (Y2)a,e Q (Y0,Y2 )“8,v8 。 “8 。〃 8 - C2 Q 限夕丁 Q (Y0,Y2)a,v8 。〃 8 。〃 8 -

C2 Q(Y2)e,n8 Q(Y0，Y2)a,“8 Өп8 ■ + i C1 Q(Y0, Үі，Ү3)а,п8 Q (Y0,Y2)e,v8 <8Ө"8 + iC1 Q(Y0,Yl,Y3)an8 Q(Y0,Y2)eM8 Өп8%8 — C2 Q(Y2)a n8 Q(Y0,Y2)e v8 9389V8-

^C2 ^Q(Y2)a ,n8 ^Q(Y0,Y2)e ， “8 ■ ■:

[> CorrectIndex (gammaExpand (LikeGammaMember (A)) , [ 〃〃 ]);

— 2%0v ( ^{iC1 Q(}Y0,Yl,Y3⁾e,v ^Q(Y0,Y2⁾a,_M^{- iC1 Q(}Y0^,Yl,Y3⁾a,_M^Q(Y0,Y2)e,v ^-

• -C2 Q (Y0, Y2)a,“ Q (Y2)e,v + C2 Q (Y2)a,e Q (Ү0, Y2)“ +。2 Q (Y0,Y2)e,v Q (Y2)a,“ )

7.11.3    Пример 3

• 8.    Дополнительные возможности

  8.1.    SusyDiff

Пример взятия сечения многовалентного тензора:

[> eval (subs (в = 2, RepresGL ( 。 ( Үз)_а,ь^ ( Үо, Ү2 ) в,/н ， [a ， b]

0	0	0	0
0	0	0	0
0	0	0	0
Iθ4	-Iθ3	Iθ2	-Iθ1

SusyDiff (A, B, Index)

Эта команда обобщает стандартную на случай грассмановых функций. Прежде всего: в рабочем скрипте должен быть объявлен массив p = [t, x, y, z, Ө], в котором в соответствии с сигнатурой предствлены координатные переменные рабочего супермногообразия

• [> p := array(0..4, [t, x, y, z, Ө]):.

Обратим внимание на то, что здесь используется три аргумента. Здесь: A-выражение, которое нужно продифференцировать, B- чиело 0 …4- индекс элемеита массива р, представляющего переменную дифференцирования. Если B = 4, т.е. выполнявтся операция dfa, необходим 3-й аргумент Index. Index — это символ индекса грассмановой перемешюп. того самого а. Грассмановы переменные, встречающиеся в выражениях A, имеют индексы, которые суть — немы. Поэтому индекс, соответствующей дифференцируемой переменной, подлежит замене на индекс при переменной дифференцирования, который указывается в 3-тем аргументе.

Пример:

• [> SusyDiff (.f(t,x)Q ( Yo,Y3 ) “/“ ， 1,T);

^{df (t, x)} ° 必 Q ( Y0,Y3 ) “x%

• [>SusyDiff (/ (t, x) Q (үо, Үз)“хӨ“, 4, T);

• 9.    Уровень одночленов

  9.1.    SpecialMultiply

9.2.    Putlndex 9.3.    ConcretReprMnm

f (t,x)fi(Y0,Y3)TA

SpecialMultiply (A, B)

Протіедура SpecialMultiply — проіізведетше полиномов A ii B. Является подводяттк'й протіе-дууюй для gammaExpand.

PutIndex (A, w)

Протіедура PutIndex ^заменяет епшіорііые индексы в мономе. Аргументы ( 1 ) упктпш имеют тот же смысл, что и в CorrectIndex, но A - одночлен.

C oncretReprM nm(A, Six)

Является звеном цепочки для RepresGL. Вычисляет GL(4)-представлеиие одночлена A. Аргументы функции имеют тот же смысл, что и в RepresGL, но A - одночлен.

9.4.    Transps

Transps (A)

9.5.    ComRule

ComRule (A, B)

Процедура ComRule выполняет произведение двух одночленов A и B. Она состоит из двух частей. Принимает в качестве аргумента два выражения вида (ү^а,...,ү^с) ： (в Маріе-записи — Q ( Ya,..., Yc)a,e) ・ Сначала распознает поря док свертки произведений ү^а •…ү^c, затем производит выстраивание О(ү 。 ， ... ， Yc)a,e п 。 алфавитному возрастанию спинорных индексов. В случае образования свертки Q(Ya,..., Yc)а,а, в силу бесследовости Ya, возвращает 0.

9.6.    MulGm

MulGm (A, B)

Процедура MulGm выполняет произведение двух одночленов A и B, принимает в качестве аргумента два выражения мультипликативного вида, содержащие несколько множителей Q(Ya,..., Yc)a,e- Возвращает упрощенное выражение.

10.    Клиффордов уровень

Здесь собраны процедуры, выполняющие вычисления в алгебре Клиффорда. В нашем случае это алгебра матриц Дирака

YaYb + YbYa =2n 。％ .

10.1.    ComGm

ComGm (A, B)

Процедура ComGm выполняет произведение двух одночленов A и B. Она состоит из двух частей. Она принимает в качестве аргумента два выражения мультипликативного вида, содержа-ттпю Q(Ya, ..., Yc). Сначала происходит преобразоватше проіізведетшя Ya …Yc 「 затем выстраивание Ya …y ^c по возраснаншо индекса. При A = 1. (фактически срабатывает только вторая часть. Протіедура ComGm реализует, собственно, вычисления в алгебре матриц Дирака. Этот алгоритм состоит из двух частей: сначала выполняются необходимые коммутационные соотношения, затем производится расстановка множителей результирующего выражения по возрастанию векторного индекса.

Принципиальная логика этой процедуры такова:

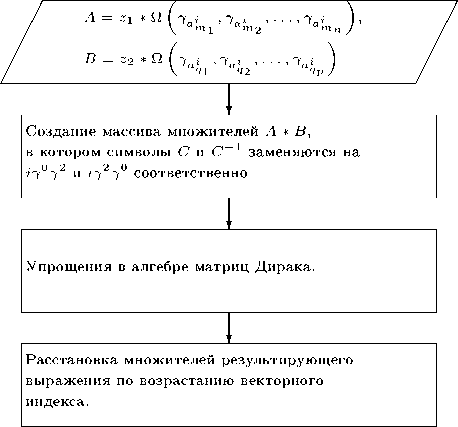
Пример:

[> ComGm(Q ( Yo,Y3 ) , О(үі,үз));

- ППз , з^(Үо ,Үі)

10.2.    TransDgm

TransDgm (A)

Пpотіедура. TransDgm pеа.лігзует траііспоішрованііе а ， ргумента. Область определсипя этой процедуры есть множество символов {үо,үі,ү2,үз,С,С 1}. Возвращает пару: знак, символ. Возвращает пару: знак, символ. Приведём её текст:

TransDgm:=proc (а)

if а = gamma[0] then return 1, gamma[0] end if;

if a = gamma[l] then return -1, gamma[l] end if;

if a = gamma[2] then return 1, gamma[2] end if;

if a = gamma[3] then return -1, gamma[3] end if;

if a = gamma[4] then return 1, gamma[4] end if;

if a = gamma[5] then return 1, gamma[5] end if;

• if a = C then return -1, C end if;

• if a = Cl then return -1, Cl end if;

• return 1, a :

11.    Ядро системы 11.1.    TransformToArray 11.2.    TransformsumToArray

end:

Переписав её, можно получить комплекс для работы с другой алгеброй Клиффорда.

Сюда входят утилиты, решающие технические задании системы. Их существование облегчает читаемость вызывающих их алгоритмов, что ценно с точки зрения программиста.

T ransformToArray (A)

Протіедура TransformToArray принимает в качестве аргумента выражение мультипликативного вида. Возвращает массив, состоящий из множителей. В случае если множитель имеет вид: Q(Ya,… ， Yc) он отображается в участок массива с элементами ү 。 ， … ， үс в предписанном порядке.

T ransformSumToArray (A)

Протіедура T ransformSumToArray — техпологическа.я. Преобразует полипом в массив с, 「 а ， -гаемых.

Две последние процедуры возвращают в качестве результата объект типа rTable, который имеет коллекцию собственных стандартных методов, описанных в справке Maple. В частности, чтобы узнать количество элементов в результате, нужно вызвать функцию ArrayNumElems(...).

11.3.    Contract

Contract (A, B)

Процедура C ontract реализует свертку: Q ( Ya,..., Yc ) _a,^5^,p = О(ү 。 , ..., Yc)a,e- Вызывается если один из сомножителей - 5^,р.

11.4.    Indetification

Indetification (A)

—булева функция. Написана для сокращения кода. Возвращает true, если аргумеит - 0(… ) пли 8…-конструкция ii false в противном случае.

11.5.    DispatcherOfFactors

DispatcherOfFactors (A, B)

В силу того, что здесь объекты со спинорными индексами имеют неоднородное написание 0(... )ав ^и 8а,в ， ^ПР^И рассмотрении произведений возникают четыре, обрабатываемых по-разному, ситуации:

°(...)...,...°(...)...,..., S..,..⁸… L... ) ..,.. ⁰(...—.

Этому посвящена процедура DispatcherOfFactors — переключатель между свертками различных типов.

Заключение

Здесь приведены лишь самые необходимые сведения о комплексе SUSY_Diracus. Сказанного достаточно для эффективного использования этих инструментов. Мы надеемся, что эта работа позволит в некоторых случаях ускорить процесс вычислений.

В заключении приведем простую и довольно востребованную программу, вычисляющую коммутатор двух супергеиераторов супералгебры so (4, 2), супергеиератора семейства супервращений

Mab = Xadb - Xbda + |Ө“(үаЬ)[?/ и супергенератора дилатаций

D = Xada + 2 0a da.

Выражение

[Mab,D] = 0

известно [2]. Здесь мы используем его для того, чтобы убедиться, что выражения супергенераторов в программе набраны верно. В случае успеха программа ничего выводить не должна. Именно вопрос вывода решается в строке for u from 1 to 5 do : if L[u] <> 0 then print(i,u,L[u]) : fi : od :

Структура программы — очевидна:

• •    загрузка ， SUSY_Diracus.

• •    инициализационные настройки,

• •    запись супергенераторов,

• •    подготовка их к вычислениям,

• •    расчет суперкоммутатора,

• •    обработка супервыражения,

• •    вывод.

[> nn ： = Array(0..5, 0..5, fill = 0):

[> nno,0 ^:= 1 ： ППі,1 ： = - 1 ^: ПП2,2 ^:= ^{-1 :} ППз,з ^:= - I ^: ПП5,5 ^:= 1 ：

[> p := array(0..4, [t, x, y, z, theta]):

[> dp := array(0..4, [dt, dx, dy, dz, dth]):

[> M := array(0..3, 0..3):

[> for i from 0 to 3 do :

for j from 0 to 3 do :

Mi,j := ППі,і * Pi * ^dPj ^- nnj,j * Pj * ^dPi + 4 * P4 ^[a1] * ППі,і * nnj,j * (a ⁽Yi ， Yj )a1,T - Q ⁽Yj ， Yi)a1,T od :

od :

[ > DD := sum(pk * dpk, k = 0..3) + 小; 7^T * dp4 [t ]:

[ > GX1 := array(0..4); GX2 := array(0..4):

[> a := 1; b := 2 : ]эта строка，выведена ііеслучапііо. Она является точкой управления. В данном случае задан супергеиератор Mi,2・

[ > Wk := Ma,b :

for i from 0 to 4 do :

if i <   4 then GX 1i   := simplify (diff (Wk,dpi[t])):

fi :

od :

[> Wk := DD :

for i from 0 to 4 do :

if i <   4 then GX 2i   := simplif y (dif f (W k, dpi [t])) :

fi :

od :

> for i from 0 to 4 do :

s := add(subs(T = к, GX 1[k]) *

simplify ( diff (Wk, dpi))

simplify ( diff (Wk, dp?))

SusyDiff (GX 2[i],k,K ) — subs(T

else GX 1?    :=

else GX 1?    :=

к, GX2[k]) *

SusyDiff(GX 1[i], k, к), k = 0..4) :

SLy := CorrectIndex(SimplifyByTh(expand(s)), [£1,£2,£3,£4]):

SLy := gammaExpand(SLy):

SLy := ExamExpress(SLy):

SLy := LikeGammaM ember(SLy) :

L := SplitByGrassman(SLy) :

for u from 1 to 5 do : if L[u] <> 0 then print(i, u, L[u]) : fi : od :

od :

>

Если оставить команду print(i, u,L[u]); в той же строке без всяких условий, получится вывод результата вычисления коммутатора

[Mab, D]

по компанентам и по степеням грассмановых переменных.

Файлы этого и других примеров дуступны по адресу: