Программный комплекс SIMPLE для определения упругих свойств слоистых волноводов с помощью бегущих волн

Определение параметров материала (упругие модули, плотность, вязкость и др.) одна из классических задач механики деформируемого твердого тела. Стандартные лабораторные методы исследования механических свойств (растяжение, кручение, индентирование и т.п.) требуют специальной подготовки образцов и нередко предполагают необратимую деформацию образца, поэтому большой интерес представляют неразрушающие методы, базирующиеся на использовании информации о взаимодействии с материалом различных физических полей, таких как рентгеновское излучение, электромагнитные и температурные поля, ультразвуковые акустические или инфразвуковые сейсмические сигналы. В отличие от прямых измерений волновые методы дают косвенную информацию о параметрах материала, для которых в этом случае обычно используется термин ≪ эффективные параметры ≫ . Они входят в виде коэффициентов в уравнения и граничные условия математических моделей, описывающих волновые процессы в рассматриваемых образцах, а задачи их определения относятся к классу коэффициентных обратных задач [1]. Эффективные параметры, найденные в результате их решения, должны обеспечивать такие же расчетные волновые характеристики, как и полученные при экспериментальных измерениях.

При акустическом или динамическом воздействии в слоистых структурах возбуждаются бегущие волны Рэлея – Лэмба, скорость распространения которых вдоль поверхности зависит не только от свойств материала, но и от толщины слоев и частоты (явление дисперсии) [2]. Это обстоятельство делает неприменимыми стандартные методы ультразвуковой дефектоскопии, базирующиеся на использовании бездиспер-сионных объемных волн, существенно затрудняя интерпретацию результатов измерений. С другой стороны, за счет дисперсии бегущие волны дают больше информации для восстановления свойств упругого волновода.

Следует отметить, что определение эффективных параметров контролируемой структуры требуется на этапе настройки модели, используемой для описания и интерпретации протекающих в ней волновых процессов. Начиная с 1990-х годов [3], для достижения этой цели разработано и проверено на экспериментальных данных большое количество методов и подходов, базирующихся на специальной обработке массивов измеренных данных с целью выделения характеристик отдельных бегущих волн на основе минимизации невязки между экспериментальными и расчетными характеристиками, например, используя генетический алгоритм [4].

Таким образом, для определения эффективных параметров диагностируемого слоистого элемента конструкции необходимо решение следующих самостоятельных задач:

• 1)    разработка и компьютерная реализация математической модели для адекватного описания волновых процессов в рассматриваемом образце;

• 2)    проведение измерений и выделение характеристик бегущих волн из экспериментально полученных сигналов;

• 3)    формирование целевой функции, учитывающей специфику задачи;

• 4)    использование эффективных алгоритмов минимизации целевой функции.

При этом следует отметить, что из-за сложности математических моделей и многочисленных методов, используемых при обработке сигналов и формировании целевых функций, эти методы трудно автоматизируются и плохо масштабируются. В результате они, как правило, работают только в руках разработчиков.

Для быстрого моделирования и наглядного описания волновых процессов хорошо зарекомендовали себя явные полуаналитические представления бегущих волн через матрицу Грина рассматриваемой волноводной структуры и параметры поверхностного источника, полученные в рамках интегрального подхода [5]. Базируясь на алгоритмах быстрого построения матрицы Грина для многослойных изотопных, анизотропных, пористых водонасыщенных и функционально-градиентных волноводов (см., например, обзор в [6]), были созданы программы определения эффективных параметров трансверсально-изотропных волоконно-армированных композитных пластин [7], нано-композитных материалов [8], многослойных изотропных [9] и поврежденных [10] волноводов, но для их тиражирования требуется создание программных комплексов с удобным пользовательским интерфейсом.

Первые версии таких программных комплексов были ранее созданы для решения прямой задачи анализа волновых полей, возбуждаемых в упругом волноводе с заданными свойствами [6], в том числе и для определения характеристик бегущих волн. В настоящей работе дается описание программного комплекса с дружественным пользовательским интерфейсом, разработанного для решения обратной задачи определения эффективных параметров упругого волновода по сигналам, регистрируемым в отдельных точках поверхности. Данная версия (программный комплекс SIMPLE : Smart Identification of Material Properties by Learning Experience) реализована для случая изотропного упругого слоя. Тем не менее она содержит все четыре указанных выше этапа и поэтому, используя уже разработанные на данный момент алгоритмы вычисления символа матрицы Грина, может быть в дальнейшем обобщена на случай волноводов более сложного строения.

1.    Интегральное представление, бегущие волны

Для моделирования волновых процессов в слоистых материалах рассматривается упругий слой, занимающий в двумерной постановке область D : |x| < да, —H <  z < 0 декартовой системы координат x = (x, z) (рис. 1). Волновое поле возбуждается заданной динамической нагрузкой q (x,t), приложенной к свободной от напряжений поверхности слоя z = 0 в некоторой ограниченной области |x| <  a.

z

q ( x,t )

v z ⁽ X , t )

x

H

Рис. 1. Геометрия проблемы

Распространение волн описывается нестационарным векторным полем смещений точек среды u ( x ,t) = (u _x ,u _z ) относительно их исходного положения. Оно характеризуется частотным спектром u( x ,w):

u( x , t)

∞

= 2П l^U^ ’

e

i ωt

dω,

∞

который в рамках линейной теории упругости описывается решением краевой задачи для уравнений Ляме – Навье для изотропной среды

(А + ^)Vdivu + ^Au + pw ² u = 0, (x, z) G D.

Упругие модули Ляме λ, µ и плотность ρ принимают постоянные значения в пределах каждого слоя D m ; w = 2nf - круговая частота, f - частота. На внешних границах заданы напряжения т = ( t _xz ,a _z ):

т | z=0 = q , т l z= - H = 0

В описываемом программном комплексе SIMPLE реализован случай однородного слоя, для которого достаточно условий (3). В общем случае многослойного пакета к ним добавляются условия жесткого сцепления слоев (непрерывность полей смещений u и напряжений τ на внутренних границах). В обоих случаях применение интегрального преобразования Фурье Fx по горизонтальной координате x позволяет получить решение рассматриваемой краевой задачи в виде контурного интеграла обратного преобразования Фурье. В традиционных обозначениях [5, 6] оно выписывается в ви- де:

u ( x ,w) = F _x 1 [U] = — [ K(a,z) Q (a)e ^{i ax}da. 2n

Γ

Здесь U = K Q - Фурье-символ искомого решения u , K(a, z) = F _x [k] и Q (a) = F _x [ q ] -Фурье-символы матрицы Грина k( x ) рассматриваемого слоистого волновода и заданной поверхностной нагрузки q (x). Столбцами k j- матрицы k = (k 1 .k ₂ ) размерности 2 х 2 являются векторы решения рассматриваемой задачи, полученные для сосредоточенных нагрузок q = 5(x)i j , j = 1,2, приложенных вдоль координатных орт І 1 = (1, 0) и i ₂ = (0,1); 5 - дельта-функция Дирака. Контур интегрирования Г идет вдоль вещественной оси комплексной плоскости волнового числа α , отклоняясь от нее при обходе вещественных полюсов Z n элементов матрицы K (a,z); направление обхода определяется в соответствии с принципом предельного поглощения. Более детально с техникой вывода представления (4) можно познакомиться в указанной выше монографии [5] и статьях из обзора в [6].

Используя лемму Жордана и теорему Коши о вычетах, общее поле источника (1) может быть представлено в виде суммы бегущих волн:

N

u(x) = £a n (z)e i^{Z n ( x - a )} + O(e ^{- Im Z} N ₊₁ ^{| x - a |} ), |Z n ||x - a| >> 1,            (5)

n=1

a n ireSK | a= — Z n ^{Q (} C n ).

Здесь N – число удерживаемых слагаемых, которые упорядочены в порядке возрастания мнимой части полюсов: ImZ n+1 > ImZ n . Первые N r вещественных полюсов дают незатухающие бегущие волны (волны Лэмба), для которых полюса ζ _n играют роль волновых чисел. Они распространяются вправо от источника с фазовыми скоростями c _n = ш/Z n и групповыми скоростями v _n = dш/dZ _n . Для n > N r мнимая часть комплексных полюсов дает экспоненциальное затухание e ^{- Im Z} n ^{| x - a |} с логарифмическим декрементом 5 _n = 2nImZ n /ReZ n . Амплитудный множитель a n зависит от свойств волновода (через матрицу K ) и параметры источника (через вектор Q ).

2.    Определение характеристик бегущих волниз экспериментальных данных 2.1.    Визуализация дисперсионных кривых, H -функция

Входными данными для определения эффективных параметров служит двумерный массив [v ij ] оцифрованных сигналов v i (t), измеренных в точках x i , расположенных на поверхности волновода z = 0 с равномерным шагом Ax: x i = x o + iAx, i = 1, 2,...N _x (рис. 1); v ij = v i (t j ), отсчеты времени t j задаются с шагом At: t j = t o + jAt размера N _x x N t . При измерении сигналов бесконтактным лазерным виброметром регистрируется скорость вертикальной компоненты смещения поверхности, поэтому полученные сигналы связаны с теоретическим нестационарным волновым полем (1) соотношением v i (t) = u _z (x i ,t), а их частотные спектры:

V i (f ) = F t [v i ] = -iшu z (x i , f ).

Двойное преобразование Фурье функции v(x,t) по x и t дает соотношение

V (a, f ) = ~iu Z J _z (a, f ) = -іш (K 21 (a, f )Q i (a, f ) + K 2 (a, f )Q ₂ (a, f)).

Очевидно, волновые числа ζ n бегущих волн в разложении (5), являющиеся полюсами элементов матрицы K(a, f ), являются также и полюсами функции V(a, f ). В рамках математической модели для визуализации дисперсионных кривых Z = Z n (f ) достаточно построить скалограмму поверхности |K ₂₂ (a, f )| на плоскости частота-волновое число. При этом значения K(a,f, Ө ) зависят от свойств волновода (для удобства вводится вектор θ , состоящий из модуля Юнга E , коэффициента Пуассона ν и плотности ρ ). На рис. 2а,б приведены такие поверхности соответственно для стали ( Ө = {207, 8 ГПа; 0, 284; 7743 кг/м ³ }) и пластика PLA, широко используемого в 3D-печати ( Ө = {3, 59 ГПа; 0, 2775; 1202 кг/м ³ }). При обработке экспериментальных данных для их визуализации к массиву [v ij ] применяется двойное дискретное преобразование Фурье по точкам x i и t j . На этой основе строится функция H(a, f ), аппроксимирующая V (a, f ):

H(a, f ) = 2AxAt

N x N t

EE v ij е^ш^ cos ax i i=0 j =0

(Учитывая симметрию, в точках -x i здесь взяты те же значения массива v ij , что дает е^гаХі + е^-гаХі = 2cosax i ).

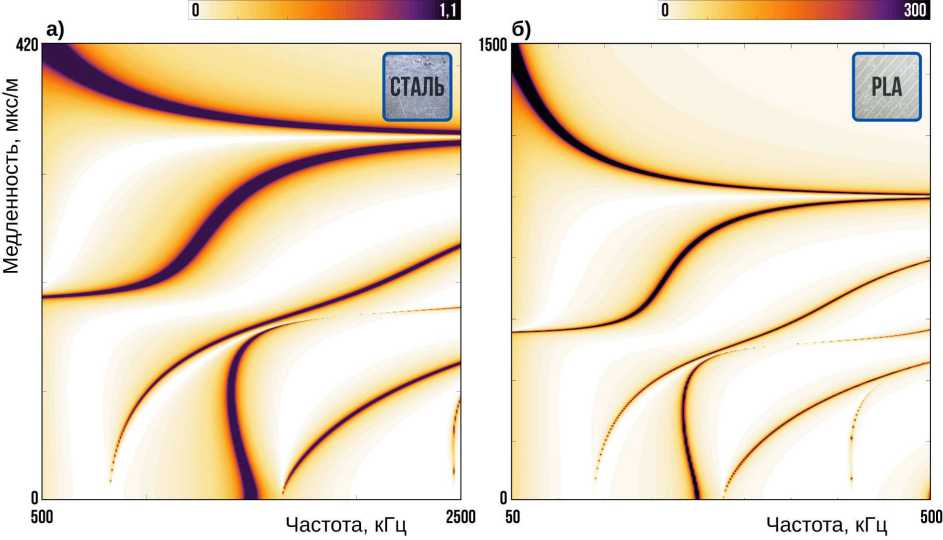
Рис. 2. Поверхности |K ₂₂ (a, f, Ө )| для стальной пластины толщиной H =1,96 мм при Ө = {207, 8 ГПа; 0, 284; 7743 кг/м ³ } (а) и пластины из пластика PLA толщиной H =3,9 мм при Ө = {3, 59 ГПа; 0, 2775; 1202 кг/м ³ }

• 2.2.    Обработка сигналов с помощью метода матричных пучков

Для извлечения информации о бегущих волнах или полюсах нестационарного сигнала наиболее целесообразным оказалось использовать метод матричных пучков (ММП) [11]. Автоматическое извлечение дисперсионных кривых с помощью ММП осуществляется в несколько шагов. Сначала к оцифрованным сигналам v _i (t j ) применяется преобразование Фурье, переводящее исходные сигналы в частотную область V (x _i , f _m ) = V _i ^m , m = 1, M f . Предполагая, что для сигнала верно представление (5), строится следующая аппроксимация:

N m

V- ^m « V ^m _z i ^{- 1}

i         a n z nm

N m

= J^ a^me^Y Z nm Ax (i - 1)

.

Здесь a _n ^m – амплитуды, связанные с собственными значениями z _nm , которые задают бегущие волны с волновыми числами ζ nm , распространяющиеся на частоте f m . ММП применяется для выделения значений z _n из последовательности данных V _i ^m .

Сингулярное разложение матрицы X, составленной из элементов последовательности данных V _i ^m , редуцируется относительно первых N _m наибольших сингулярных значений, причем для каждой частоты f _m может быть выбрано свое значение N _m . Для оценки полюсов необходимо найти N m собственных чисел z, позволяющих определить волновые числа ζ _nm , из условия:

U* • X • W* - zS, где S = diag{ai,...,aNm} - диагональная матрица, составленная из наибольших сингулярных значений, а U и W соответствующие урезанные унитарные матрицы SVD разложения.

После процедуры пост-обработки, оставляющей только значения ζ _nm , соответствующие распространяющимся бегущим волнам (т.е. удаляющей |Im Z nm H | > Г где

ǫ достаточно мало и выбирается так, чтобы исключить из рассмотрения все быстроза-тухаюшие моды с мнимыми волновыми числами), формируется набор медленностей s nm = Z nm /f m , который в дальнейшем может использоваться для решения обратной задачи по определению упругих свойств волновода.

• 2.3.    Решение обратной задачи

Задача оценки эффективных параметров волновода Ө в области Ө, которая определяется значениями верхней и нижней границ для каждого из параметров вектора θ , сводится к решению оптимизационной задачи

Ө = arg min g( Ө , s').                                    (8)

Целевая функция задается путем подстановки найденных экспериментально медлен-ностей s mn в элементы матрицы Грина и их последующего обращения:

M

• 1    f

3.    Описание программного комплекса SIMPLE 3.1.    Структура и основные функции программного комплекса

g^{( ө ,s )} = м^ 52 EE^min (\^K-p4f_mj mn ,о, ^{ө )} |, ^в ) .          (9)

m=1 k eP m l p

Здесь n – индекс для нумерации медленностей, полученных для каждой частоты fm после пост-обработки, т.е. Pm = {n \Bsnm}, m = 1,Mf, Mf — число всех рассмат-Mf риваемых частот, а M = £ \Pm\ — общее число существующих пар медленностей. m=1

Использование функционала вида (9) позволяет избежать трудоемкой процедуры поиска полюсов Фурье-символа матрицы Грина, а дополнительный параметр β , определяемый по средним значениям \K — 1 (а, f )\, вводится для повышения эффективности на этапе решения обратной задачи, чтобы удалить слишком большие значения целевой функции в силу возможного наличия шума в исходных данных. Тем не менее в этом случае сохраняется неопределенность в выборе начального приближения θ , поскольку, как известно, выбор начального значения может достаточно сильно влиять на результат. Данная проблема решается путем нахождения набора оптимизационных решений Ө на равномерной сетке начальных приближений Ө в области Ө С Ө с последующим усреднением результата. Выбор конечного решения может быть реализован в терминах математической статистики через оценку центра группирования выборки (среднее, моду, медиану).

Основная функция программного комплекса SIMPLE состоит в определении упругих модулей слоистых материалов по экспериментальным данным, обработка которых требует дополнительной настройки и контроля на промежуточных этапах. Общая схема принципа функционирования SIMPLE с точки зрения пользователя изображена в виде схемы на рис. 3.

В качестве входных данных SIMPLE может использовать двумерный массив оцифрованных сигналов [v ij ] в точках x i либо значения медленностей mnn для заданного массива частот f m (блоки зеленого цвета). В первом случае необходимо применение ММП для получения значений s _mn . Кроме того, предусмотрена возможность

Генерация синтетических дисперсионных характеристик

Импорт нестационарного сигнала

Применение метода матричного пучка

Дисперсионные характеристики

Импорт обработанных дисперсионных характеристик

г Фильтрация дисперсионных характеристик

Экспорт дисперсионных

^л характеристик

Экспорт двумерного

/ преобразования Фурье /

Определение начального приближения

Экспорт теоретических дисперсионных характеристик

Экспорт теоретических значений

/         матриц Грина

Решение оптимизационной задачи ]

Упругие свойства

Экспорт статистических данных

Рис. 3. Общая схема принципа функционирования SIMPLE (пользовательский уровень)

генерации синтетических данных согласно алгоритму предложенному в [12], для верификации алгоритма при известных значениях θ и изучения влияния настроек программы на результат.

В программе можно производить предварительную обработку и фильтрацию дисперсионных кривых как с помощью настройки параметра ММП M f для разных частотных диапазонов, так и путем удаления шума вручную, используя интерактивный инструмент типа лассо. На этом же этапе пользователь может построить графики и экспортировать соответствующие данные об экспериментальных дисперсионных кривых или двумерном преобразовании Фурье входного сигнала. При настройке параметров SIMPLE в помощь пользователю выводит графики медленностей и затухания для каждого из регулируемых промежутков частот.

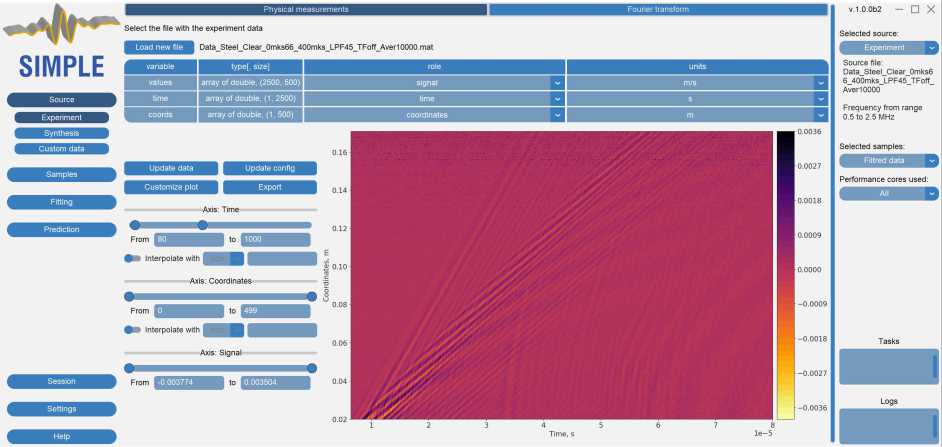
Рис. 4. Примеры окна SIMPLE при обработке экспериментальных данных (В-скана) для пластины толщиной 1,96 мм

После подготовки данных о дисперсионных свойствах материала пользователь может переходить к разделу, в котором определяются настройки метода решения оптимизационной задачи, задаются известные и неизвестные характеристики упругого слоя (физико-механические и геометрические свойства), а также выбирается массив начальных приближений θ и область Θ ⊂ Θ, в которой равномерно распределяются значения. Результаты решения оптимизационной задачи для каждого начального приближения сохраняются в отдельный файл, а интерфейс программы выводит гистограммы распределений оценок параметров для каждой компоненты вектора θ .

В SIMPLE также предусмотрена возможность сохранения и загрузки сессий, настроек программы и раздел с информацией о ней. Так как время выполнения большинства процедур занимает от нескольких секунд до нескольких часов (например, при решении обратной задачи с использованием большого массива начальных приближений), то в приложении выводится информация о текущих выполняемых задачах, логи и некоторые другие детали (например, время выполнения процедуры и примерная доля выполненных вычислений). Вид пользовательского окна (вкладка Source для загрузки массива сигналов) для измерений, сделанных с помощью лазерной допплеровской виброметрии на образце из стали, приведен на рис. 4.

• 3.2.    Программная реализация средствами ЯП Python

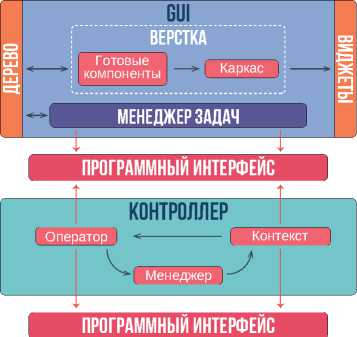
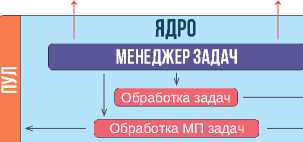
Программа SIMPLE написана на Python 3.12 и представляет слабосвязную модель, состоящую из тр¨ех основных блоков: контроллера, ядра и GUI (англ. graphical user interface – графический интерфейс пользователя). Общая схема функционирования SIMPLE на программном уровне схематически показана на рис. 5.

Ведение журнала: Loguru

Сборка: Pyinstaller

Вычисления: NumPy с MKL

Общие:

CustomTkinter, Pillow

Готовые компоненты:

Matplotlib

Валидация данных: Pydantic

Вычисления:

SciPy с MKL

Повышение производительности: Cython

Рис. 5. Общая схема принципа функционирования SIMPLE (программный уровень)

Блок контроллера взаимодействует с GUI и ядром через соответствующие программные интерфейсы, что дает необходимую гибкость и независимость. В нем осуществляется контроль за жизненным циклом элементов приложения с помощью шаблона проектирования ≪ Контекст ≫ и связью между GUI и ядром (шаблон ≪ Опера-тор ≫ ). Здесь и далее под шаблоном проектирования подразумевается программная архитектурная конструкция, а название шаблонов по возможности отражает сущность и не обязательно соответствует одному из шаблонов с аналогичным названием в области проектирования программного обеспечения. Контролем и согласованием задач, а также адаптацией пересылаемых данных занимается специальный менеджер.

Ядро занимается управлением базой данных (БД) и обработкой задач с поддержкой многозадачности, а для многопроцессорных (МП) задач используется собственный специализированный пул. Расчеты производятся в векторизованном виде с использованием библиотек NumPy и SciPy, что позволило снизить вычислительные затраты при решении возникающих оптимизационных и алгебраических задач. Для увеличения точности и скорости вычислений их сборка была выполнена на базе пакета Intel OneAPI с использованием библиотеки MKL. Дополнительную производительность отдельных модулей обеспечивает библиотека Cython.

Тесты данной программы показали, что при использовании МП обработки наиболее эффективным подходом является задействование только одного гипер-потока от каждого используемого ядра процессора с помощью модуля psutil. Так как в современных процессорах применяются два типа ядер (производительные и энергоэффективные), то для их различения средствами Python был создан интерфейс из стандартной Windows-библиотеки kernel32.

GUI верстается в рамках шаблонов ≪ Готовые компоненты ≫ и ≪ Каркас ≫ , которые связаны посредством специально созданного инструмента ≪ Дерево ≫ и размещены на каркасе приложения. GUI не выходит за рамки одного основного окна, дочерние окна не создаются. В нем используется специально разработанная на базе библиотеки CustomTkinter оболочка ≪ Виджеты ≫ , которая обеспечивает необходимую функциональность. Для работы с изображениями используется библиотека Pillow, а для построения графиков – matplotlib. Чтобы настроить внешний вид окна и обеспечить его функциональность используются стандартные библиотеки Windows – user32 и dwmapi.

• 3.3.    Пример использования программного комплекса SIMPLE для экспериментальных данных

  В качестве примера работы программного комплекса SIMPLE были рассмотрены сигналы, полученные с помощью лазерной виброметрии, для образцов из стали и пластика PLA (поверхность В-скана для образца из стали приведена на рис. 4). Плотность и толщина каждого образца были измерены традиционными способами, а значения модуля Юнга и коэффициента Пуассона определялись с использованием 10000 начальных приближений равномерно распределенных в областях Ө = {[185; 225] ГПа, [0, 27; 0,43], 7743 кг/м ³ } и Ө = {[2,1;4, 9] ГПа; [0, 27; 0,43]; 1202 кг/м ³ } для стали и пластика соответственно, при этом область поиска выбиралась немного шире: Ө = {[180; 230] ГПа; [0, 25;0,45];7743 кг/м ³ } и Ө = {[2; 5] ГПа; [0, 25;0,45];1202 кг/м ³ }. Гистограммы распределений модуля Юнга и коэффициента Пуассона, полученных в результате решения оптимизационной задачи (8) приведены на рис. 2, на котором можно видеть достаточно небольшой разброс результатов при решении обратной задачи.

Пример скалограммы поверхности H -функции в той же плоскости (f, а), что и на рис. 2, а также теоретические (рассчитанные по найденным значениям θ ) и экспериментальные значения медленностей приведены на рис. 7. Для иллюстрации эффективности применения предложенного подхода для различных материалов, рассматривается стальная пластина и образец из пластика. Точность аппроксимации двойного интеграла преобразования F t,x зависит от шагов дискретизации Ax, At и числа точек N x ,N t , поэтому на рис. 7 нет таких четких линий, как на рис. 2. Это скорее размытые пятна, но их центры, тем не менее лежат на показанных квадратными маркерами точках, соответствующих дисперсионным кривым, что дает основание использовать точки (f pm , Z m ) локальных максимумов функции H в качестве приближения характеристик возбуждаемых бегущих волн, определенных по экспериментальным данным.

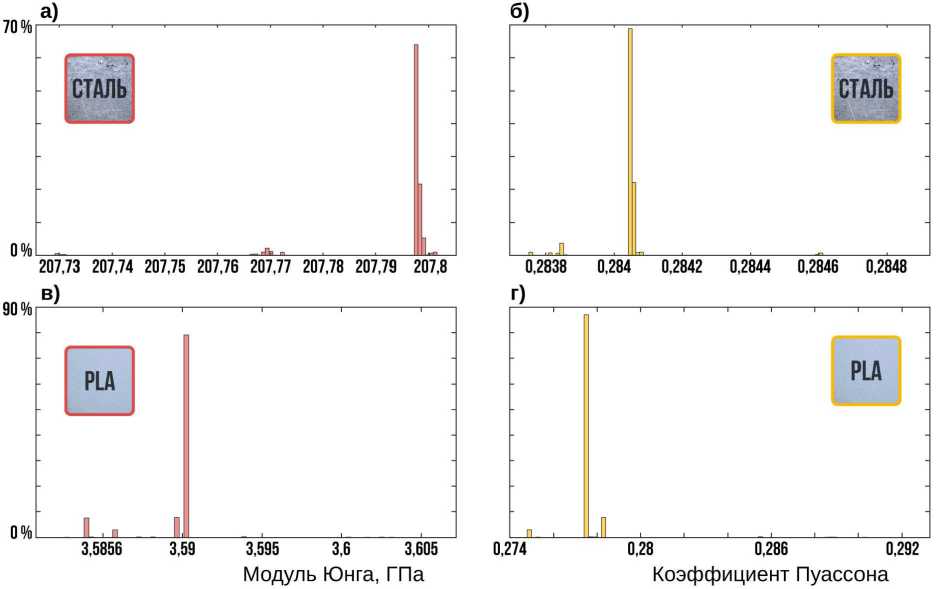
Рис. 6. Гистограммы распределений оценок параметров: модуля Юнга (а, в) и коэффициента Пуассона (б, г) для образцов из стали (а, б) и пластика PLA (в, г)

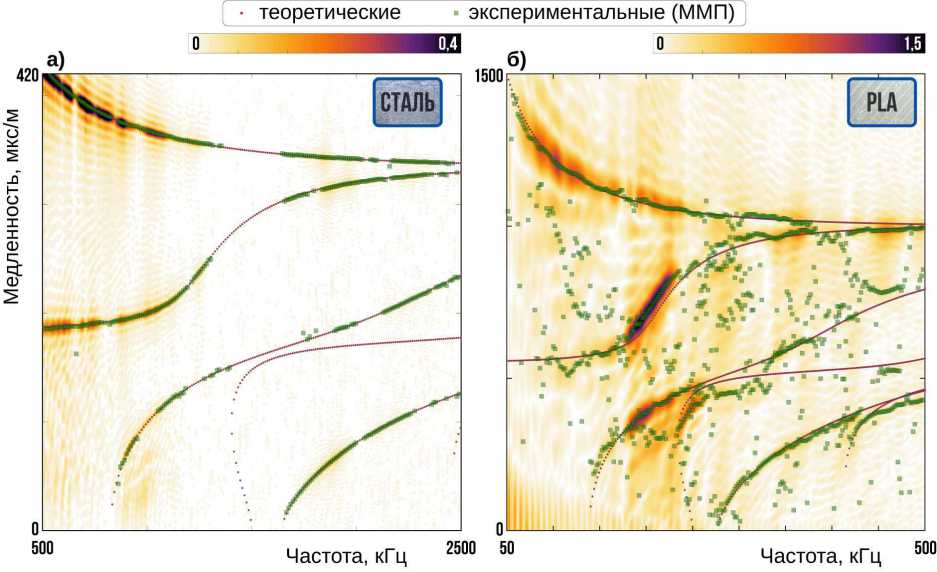
Рис. 7. Поверхности |H (a,f, Ө ) |, теоретические (круглые маркеры) и экспериментальные (квадратные маркеры) медленности для стальной пластины толщиной H = 1, 96 мм при Ө = {207, 8 ГПа; 0, 284; 7743 кг/м ³ } (а) и пластины из пластика PLA толщиной H = 3, 96 мм при Ө = {3, 59 ГПа; 0, 2775; 1202 кг/м ³ }

Для верификации естественно сравнить теоретические и экспериментальные значения медленностей (snm и smn) для каждого из двух рассмотренных образцов. Анализ показывает очень хорошее совпадение медленностей для образца из стали (рис. 7а). Для образца из пластика имеет место достаточно сильное затухание сигнала, а также более интенсивный шум, проявляющийся как в дополнительных точках, не соотносящихся с определенной дисперсионной кривой, так и в осцилляции в окрестности проявляющихся кривых. В результате решения обратной задачи, как можно видеть на рис. 7б, не все теоретические дисперсионные кривые достаточно хорошо согласуются с экспериментальными данными. Например, остается заметное расхождение кривых для моды S0 в частотном диапазоне между 150 и 250 кГц. Следует отметить, что такое расхождение для пластика PLA, в первую очередь, связано со свойствами пластиков, обладающих, например, заметно большей вязкостью, чем металлы, и погрешностью проведения эксперимента, а не ошибками разработанного алгоритма.

Заключение

Разработанный программный комплекс SIMPLE позволяет определять механические свойства слоистого изотропного волновода на основе ультразвуковых сигналов, регистрируемых в некоторых точках поверхности волновода. В данной статье приводится описание работы программы на примере определения эффективных параметров упругого однородного изотропного слоя. Архитектура программного комплекса спроектирована с уч¨етом классических паттернов проектирования, что позволяет быстро расширять его функционал без существенных изменений в структуре. Например, в дальнейшем можно обобщить подход на случай волноводов более сложного строения, для чего могут быть добавлены имеющиеся алгоритмы для построения Фурье-символов матриц Грина для анизотропных, многослойных и поврежденных волноводов. В SIMPLE также может быть добавлена возможность использования GPU как для ускорения отображения GUI, так и для выполнения затратных с точки зрения вычислений алгоритмов.

Работа выполнена в рамках проекта РНФ № 24-11-00140.