Проникновение электрического поля из приземного слоя атмосферы в ионосферу

Математическому моделированию крупномасштабных электрических полей в атмосфере Земли посвящены многочисленные работы. Наряду с анализом полей, создаваемых грозовыми облаками, в последние годы исследуются процессы, связывающие ионосферу с атмосферой и литосферой. Прикладная направленность моделирования этих процессов обусловлена желанием использовать космические средства для обнаружения предвестников землетрясений. Имеются экспериментальные данные об изменениях электрического поля в приземной атмосфере накануне землетрясений. Поскольку покрыть Землю сетью наземных датчиков проблематично, возник вопрос, можно ли судить об этих полях на основе спутниковых измерений в верхней ионосфере. Обзор работ по данной теме можно найти в монографии [Molchanov, Hayakawa, 2008], где рассматриваются различные механизмы влияния литосферы на ионосферу.

Одним из простейших механизмов литосферноионосферной связи является проникновение электрического поля в ионосферу через атмосферный проводник. В рамках такой модели результаты, полученные в работах [Denisenko et al., 2008b; Grimal-sky et al., 2003; Pulinets et al, 2003], существенно различаются, хотя используется одна и та же квази-стационарная модель электропроводности атмосферы с близкими пространственными распределениями атмосферной проводимости. Принципиальное различие состоит в способе учета замыкания токов через ионосферу.

Для уравнения электропроводности, которое решается во всех трех моделях, на верхней границе атмосферы ставится условие Неймана [Pulinets et al, 2003], Дирихле [Grimalsky et al., 2003] или некоторое специальное условие, связывающее производные по нормальному и касательным направлениям к границе [Denisenko et al., 2008b]. Предложенное нами условие детально сформулировано ниже и соответствует закону сохранения заряда для ионосферы, рассматриваемой как проводник с бесконечной продольной проводимостью. Первые два условия получаются в предельных случаях нулевой или бесконечной педерсеновской проводимости ионосферы.

Уравнение электропроводности

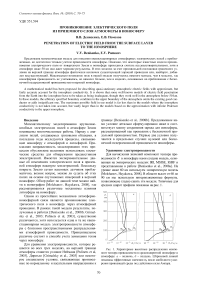
Для вычисления значений компонент тензора проводимости σ ˆ в ионосфере нами создана модель, основанная на эмпирических моделях IRI, MSISE, IGRF и представленная в работе [Denisenko et al., 2008a]. На уровне ниже 60 км используем эмпирическую модель [Molchanov, Hayakawa, 2008]. В области высот от 60 до 90 км мы используем интерполяционные формулы, позволяющие гладко сшить эти модели . Типичные для средних широт профили показаны на рис. 1.

IO"15 IO"10 IO"5 о, См/м IO"15   IO"10 IO”5 о, См/м

Рис . 1. Характерные высотные распределения компо нент тензора проводимости в среднеширотной ионосфере и атмосфере : а – полночь , б – полдень . Штриховой линией показаны эффективные значения σ _P после свободного уско рения проводящей среды под действием силы Ампера .

Уравнение электропроводности для электрического потенциала V имеет вид

- div ( σ ˆ grad V ) = q ,

где – q – дивергенция заданных сторонних токов, q =0 в нашей модели.

Для локальных явлений кривизной поверхности Земли можно пренебречь, тогда рассматриваем атмосферу как плоский слой и используем декартовы координаты x , y , z с осью Z, направленной вверх. Плоскость z =0 – поверхность Земли.

Задача существенно упрощается, если магнитное поле вертикально и проводимость зависит только от высоты. В этом случае холловская проводимость не учитывается, и остаются только педерсеновская σ P и продольная σ _|| проводимости:

, _х ( д ² v д ² v ) д ( , a v ) ^-а р ( z ) I . -+ — I^- "Erl ^a"( z)4T I = q , ^ д x     д y ) д z V       д z )

но после нахождения потенциала при вычислении плотности тока j следует учесть холловскую проводимость σ_H.

На нижней границе атмосферы, т. е. на плоскости z =0, во многих моделях задается вертикальная компонента электрического поля, для чего используются некоторые представления, основанные на результатах измерений,

= 0 = E 0 ( x , y ), (3)

∂ V ∂ z

хотя было бы правильнее говорить о задании на этой границе нормальной компоненты плотности тока, которая поддерживается находящимся под землей генератором. При известной проводимости приземной атмосферы эти условия эквивалентны.

Ограничимся рассмотрением конечного по высоте слоя ионосферы z < z _∞. Например, область выше z _∞=500 км вносит вклад менее 1 % в существенные для рассматриваемой задачи интегральные параметры проводимости. На высоте z _∞ может быть задана вертикальная компонента плотности тока

= j _∞ ( x , y ) (4)

z = z _∞

∂ V

-σ _||( z _∞ ) ∂ z

или учтены токи в удаленных проводниках, соединенных вдоль идеально проводящих магнитных силовых линий с точками этой границы, как это будет сделано ниже.

Образно говоря, магнитные силовые линии в верхней ионосфере и выше можно рассматривать как пучок проводов, каждый из которых покрыт слоем почти идеального изолятора, и их оголенные концы погружены в проводящую среду E- и F-слоев ионосферы. Соединяемые этими «проводами» точки в Северном и Южном полушариях называются сопряженными. Значения потенциала в сопряженных точках равны в силу бесконечной проводимости вдоль силовой линии. Такое наличие сопряженных точек характерно для средних широт, и при симметрии полушарий имеем j _∞=0. Из полярных шапок магнитные силовые линии уходят в дальний хвост магнитосферы, где σ_P, σ_H пренебрежимо малы, и на таких линиях можно над ионосферой полагать j _∞=0.

Есть еще одна особенная группа магнитных силовых линий. Эти линии начинаются в авроральных зонах и уходят в плазменный слой магнитосферного хвоста, где σP настолько велика, что ее интегральное значение в десятки раз превосходит аналогичный ионосферный параметр. В этом случае магнитосферная проводимость должна быть учтена. Ниже мы оценим роль магнитосферного проводника и сопряженной ионосферы.

Чтобы объяснить принципиальные различия в результатах моделирования, полученных в работах [Denisenko et al., 2008b; Grimalsky et al., 2003; Pulinets et al, 2003], рассмотрим сравнительно простой случай, когда электрическое поле не зависит от одной горизонтальной координаты y и является периодическим по x . Тогда электрический потенциал может быть представлен в виде f ( z ) cos( x / x ₀) . Для функции f ( z ) из уравнения (2) получается обыкновенное дифференциальное уравнение с граничными условиями (3), (4). Такую краевую задачу несложно решить численно, поскольку большее электрическое поле проникает в ионосферу ночью, используем типичные для ночи профили проводимости, показанные на pис. 1, а . Для того чтобы проанализировать зависимость от горизонтального масштаба поля, расчеты проведены для трех значений x 0 =10, 100, 1000 км.

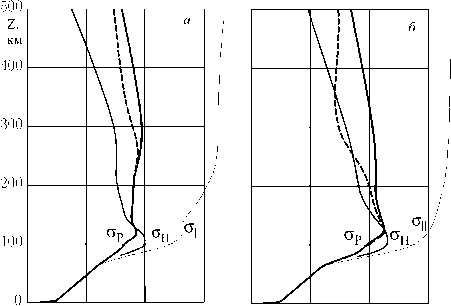
На pис. 2, а представлены высотные распределения горизонтальной компоненты поля E _x ( π x ₀ /2, z ) над точкой x = π x ₀ /2, где достигается ее максимальное по x значение. Максимальные значения вертикальной компоненты поля E_z (0, 0) определены граничным условием (3) и у всех трех решений равны 100 В/м. Горизонтальная компонента электрического поля остается постоянной выше приведенной на pис. 2 области высот до верхней границы расчетной области z =z_∞. При выборе z _∞=500 или 1000 км результаты отличаются менее чем на 1 % и не видны в масштабе рисунка.

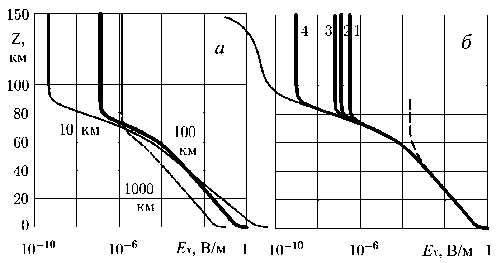
Рис . 2. Высотные распределения горизонтальной ком поненты электрического поля E_x : а – E_x , полученные в результате расчетов при различных горизонтальных мас штабах ( тонкая , жирная , штриховая линии соответствуют x ₀ =10, 100, 1000 км ); б – сравнение наших результатов ( жирные линии 1–4) с моделями [Pulinets et al, 2003] ( штриховая линия ) и [Grimalsky et al., 2003] ( тонкая ли ния ) при x 0 =100 км . Кривая 1 – при проводимости , уменьшенной за счет ускорения проводящей среды под действием силы Ампера в течение часа . Кривая 2 совпада ет с жирной кривой на p ис . 2, а . Кривая 3 – при добавле нии к Σ _P проводимости сопряженной ионосферы . Кривая 4 – при добавлении к Σ P проводимости плазменного слоя , равной 100 C м .

При характерном горизонтальном масштабе x 0 =100 км, когда ширина областей с положительным или отрицательным знаком вертикальной компоненты поля E z ( x , 0) составляет 314 км, в ионосфере получается поле E x около 0.1 мкВ/м.

На pис. 3, а жирной кривой представлены соответствующие высотные распределения горизонтальной компоненты плотности тока j x при горизонтальном масштабе x ₀=100 км. Аналогичный профиль для дневных условий показан на pис. 3, б . Поскольку выше 90 км E_x практически постоянно, профиль j_x повторяет профиль педерсеновской проводимости. На pис. 3, б хорошо видно, к чему приводит уменьшение эффективной педерсеновской проводимости, получающееся в результате ускорения среды под действием силы Ампера: токи в F-слое ионосферы практически исчезают, и весь горизонтальный ионосферный ток сосредотачивается в E-слое. В ночной ионосфере, как видно на pис. 3, а , ситуация сложнее. Поскольку изначально проводимость F-слоя многократно превосходила проводимость E-слоя, ускорение в течение часа лишь несколько перераспределяет токи из F- в E-слой.

Двумерная модель ионосферного проводника

Теперь обратимся непосредственно к моделям [Denisenko et al., 2008b; Grimalsky et al., 2003; Pulinets et al, 2003], каждая из которых дает свое приближенное решение задачи электропроводности. Во всех трех моделях используется существенная анизотропия проводимости для упрощения моделирования ионосферы за счет уменьшения расчетной области с помощью некоторого граничного условия на некоторой высоте z up << z ∞ . Мы построим решения того же вида f ( z )cos( x / x ₀) с граничными условиями, использованными в этих моделях, чтобы показать и объяснить отличия. Хотя мы попутно продемонстрируем роль проводника в магнитосферном плазменном слое и сопряженной ионосфере, в указанных моделях она не учитывается, и поэтому построенное выше решение с условием (4) при j ∞ =0 можно рассматривать как точное, к которому рассмат-

Рис . 3. Высотные распределения горизонтальной ком поненты плотности тока j_x : а – ночь , б – день . Наша мо дель – жирные кривые . Штриховая линия – при эффек тивной педерсеновской проводимости , получающейся после ускорения среды под действием силы Ампера в течение часа . Кривые 1 – модель [Pulinets et al, 2003]. Кривые 2 – модель [Grimalsky et al., 2003].

риваемые модели дают свои приближения. Начнем с нашей модели [Denisenko et al., 2008b], предварительно отметив, что наша версия двумерной модели ионосферного проводника для ионосферы с близким к реальному геомагнитным полем подробно представлена в статьях [ Денисенко , 2002 Denisenko et al., 2008a].

Отделим основную часть ионосферы от нижней ионосферы плоскостью z = z up , и в основной части ионосферы будем использовать приближение σ _|| = ∞ . Как видно на pис. 1, выше 100 км σ _|| на несколько порядков превосходит остальные компоненты тензора проводимости. Это приближение не справедливо в нижней ионосфере, и минимально возможное значение параметра z up , при котором еще не вносится заметная погрешность, выбирается с помощью тестовых расчетов.

Эквипотенциальность вертикальных магнитных силовых линий означает независимость горизонтальных компонент напряженности электрического поля E x , E y от высоты, и поэтому с помощью интегрирования закона Ома по высоте может быть получен двумерный закон Ома с педерсеновской и холловской интегральными проводимостями Σ P , Σ H :

( J, ) ГЕр-Ен YEx )

x   PH x

I I I у у || E ,

V Jy ) VEH EP JV Ey J z∞

E P   I   ^P dz, zup

E H = I z “ o H dz .                                (5)

z up

Таким образом, получается двумерная модель верхней ионосферы, в которой каждая точка с координатами x , y представляет целую магнитную силовую линию – вертикальный отрезок z up < z < z ∞ в рассматриваемом случае. Такая ионосфера эквивалентна тонкой проводящей пленке с двумерным законом Ома (5). Эта упрощенная модель позволяет сформулировать условие, соответствующее закону сохранения заряда: токи, приходящие снизу через границу z = z up , и заданные условием (4) токи j ∞ ( x , y ), приходящие через верхнюю границу z = z ∞ , растекаются по ионосфере:

+ Q ,                   (6)

z = z _up

-         d V div J = -σ||(z∞) ∂z

где Div означает поверхностную дивергенцию, в отличие от div. В правую часть добавлена заданная функция Q ( x , y ), которая позволяет учесть источники заряда в этом слое и токи выше ионосферы j _∞( x , y ), если таковые существуют.

Поскольку рассматриваем явления с горизонтальным масштабом, малым по сравнению с ионосферными масштабами, составляющими в средних широтах тысячи километров, Σ_P и Σ_H можно считать не зависящими от x , y , и тогда полученные параметры Σ P , Σ H являются константами. Постоянная холловская интегральная проводимость выпадает из равенства (6) и получается

( d ² V d 2 V'

^P V d x ² +d y²

+σ || ( z up ) _{∂ z} z = z _up = Q .    (7)

z = z _up

Возможность отделения основной части ионосферы с помощью граничного условия (7) проверена сравнением решений, полученных с использованием этого условия, с решениями во всей области до z = z ∞ . При z up =90 км и x 0 =100 км различие в горизонтальной компоненте электрического поля E x не превосходит половины процента. Для трех кривых на pис. 2, а различие не видно в масштабе рисунка. Необходимая высота постановки граничного условия (7) растет с уменьшением горизонтального масштаба решения x 0 . Так, использованное нами в работах [Ampferer et al., 2010; Denisenko et al., 2008b] отделение ионосферы от атмосферы с помощью граничного условия (7) на высоте z up =90 км вносит погрешность в величину ионосферного E x менее 1 % для полей с горизонтальным масштабом x 0 >3 км.

Сравнение с другими моделями

Аналогичные решения несложно построить и с граничным условием, которое использовано в модели [Pulinets et al, 2003]:

d V d z

= 0, z=90 км

или в модели [Grimalsky et al., 2003]:

V I z = 150 км = 0. (9)

Последнее условие было бы справедливо при наличии идеального проводника выше 150 км, причем с высокой проводимостью в горизонтальном направлении.

Условие (8) эквивалентно равенству нулю тока из атмосферы в ионосферу и поэтому соответствует замене хорошо проводящей ионосферы выше 90 км изолятором. Эти граничные условия получаются из нашего условия (7) при Σ P =0 (8), или Σ P =∞ (9).

На pис. 2, б показаны результаты расчетов при характерном для всех трех моделей горизонтальном масштабе x ₀=100 км. Как видим, пренебрежение проводимостью ионосферы за счет условия (8) приводит к увеличению ионосферного поля E_x на три порядка, а абсолютизация этой проводимости условием (9) дает на четыре порядка меньшее E x на высоте 100 км и строго нулевое поле выше 150 км.

Можно отметить, что если учесть сопряженную ионосферу, т. е. удвоить Σ P , ионосферное поле E x уменьшится вдвое. Такое поле показано кривой 3 на pис. 2, б . Если рассмотреть процесс в авроральной зоне и для учета магнитосферной проводимости добавить к Σ P характерную проводимость плазменного слоя 100 См, E_x уменьшится в 140 раз – кривая 4, но останется намного больше показанного тонкой линией на pис. 2, б поля в модели [Grimalsky et al., 2003]. Если наоборот, учесть уменьшение эффективной проводимости, показанное штриховой линией на pис. 1, а , ионосферное поле E x увеличится в 2.5 раза – кривая 1, что лишь незначительно уменьшит тысячекратное отличие от модели [Pulinets et al, 2003]. Результат расчета в рамках модели [Pulinets et al, 2003] показан штриховой линией на pис. 2, б .

На pис. 3, а показаны соответствующие pис. 2, б распределения горизонтальной компоненты плотности тока. Аналогичные токи при дневной проводи- мости показаны на pис. 3, б. Наша модель – жирные кривые. Штриховая линия – при эффективной пе-дерсеновской проводимости, получающейся после ускорения среды под действием силы Ампера в течение часа. Поскольку полный ток задан наземным источником и является единым для всех приведенных моделей, площади левее всех кривых совпадают. Однако это трудно показать в масштабе одного рисунка.

Кривые 1 представляют модель [Pulinets et al, 2003]. В этой модели ток не может идти на уровне выше 90 км, и поэтому весь ток замыкается ниже этого уровня. При этом плотность тока j_x возрастает с высотой в соответствии с ростом проводимости и достигает на уровне 90 км гораздо большей величины, чем при реальном замыкании по всей ионосфере, и скачком убывает до нуля на уровне выше 90 км. Поэтому на pис. 3, а , б показаны только части соотвествующих графиков, вошедшие в рисунок.

Кривые 2 представляют модель [Grimalsky et al., 2003]. В ней горизонтальная компонента плотности тока в ионосфере мала и неотличима от нуля в масштабе рисунка, поскольку выше 150 км лежит идеальный проводник, по поверхности которого почти весь ток и замыкается, т. е. j_x ( z ) имеет особенность в виде дельта-функции, которую тоже трудно нарисовать.

В атмосфере на уровне ниже 50 км все модели дают одинаковые j x , как и E x . Можно сказать, что для полей и токов в этой части атмосферы важно лишь то, что ионосфера имеет проводимость в горизонтальном направлении, намного большую, чем атмосфера, а это свойство во всех трех моделях соблюдено.

Широко известна еще одна модель проникновения электрического поля в ионосферу. Полученные на ее основе возмущения ионосферы представлены в статье [Лаптухов и др., 2009], а собственно модель усиления ионосферного электрического поля – в [Сорокин, Чмырев, 2002]. От рассмотренных выше трех моделей [Denisenko et al., 2008b; Grimalsky et al., 2003; Pulinets et al, 2003] модель [Сорокин, Чмы-рев, 2002] отличается добавлением сторонних токов. Авторы полагают, что существует сторонний вертикальный ток, плотность которого экспоненциально убывает с высотой. В приведенных оценках использовано значение j s = 3 -10 ⁹ А / м 2 около поверхности земли с декрементом 1/ H =1/(2 км). Этот ток обеспечен диффузией положительно заряженных частиц аэрозоля, плотность которых у поверхности земли составляет N ₊ = 4 - 10⁹ м"³.

При заряде частицы, равном заряду электрона e , несложно вычислить плотность потока частиц j _s / e , которая в силу диффузионной природы потока пропорциональна градиенту концентрации:

- = - K N, (10) e о z где K – коэффициент вертикальной турбулентной диффузии в приземной атмосфере. Заряд частицы q равен заряду электрона в оценках авторов [Сорокин, Чмырев, 2002]; без объяснений обозначение q введено в статье [Сорокин и др., 2001], описывающей модель [Сорокин, Чмырев, 2002]. Если полагать, что убывание стороннего тока обусловлено убыванием концентрации заряженных частиц аэрозоля, то градиент примерно равен N+/H. Из (10) получаем оценку K = jsH / (eN+) = 104 м2 / с . В правой части (10) мы пренебрегли скоростью оседания частиц, иначе K должен быть еще больше. Чтобы представить этот масштаб K, достаточно заметить, что стометровые неоднородности сглаживались бы за секунду, чего в земной атмосфере, конечно, не бывает. В справочниках по физике атмосферы 1 м2/с характеризуется как максимальное по порядку величины значение K, т. е. в обсуждаемой модели [Сорокин, Чмырев, 2002] коэффициент вертикальной турбулентной диффузии в приземной атмосфере завышен в тысячи раз. В статье [Sorokin et al., 2005] авторы изменили набор параметров. При этом значение K, оцененное по формуле K = jsH / (eN+), еще увеличивается.

Но даже в столь чрезвычайно турбулизованной атмосфере такой сторонний ток не может существовать как квазистационарный. Дело в том, что речь идет о нескомпенсированных зарядах, но если в проводящую среду внести некоторый заряд, он будет скомпенсирован за счет токов проводимости за время порядка ε 0 /σ. Это время не превосходит 10 минут, поскольку проводимость σ обычно больше 2∙10^–14 См/м около поверхности Земли и быстро растет с высотой, и именно такое высотное распределение проводимости использовано в обсуждаемой модели [Сорокин, Чмырев, 2002].

Когда же положительные частицы будут окружены отрицательными частицами той же концентрации, перенос воздуха, содержащего все эти частицы, даст почти нулевой суммарный сторонний ток. Строго говоря, в обсуждаемой модели сохранение зарядов частиц, осуществляющих сторонний ток, требуется только в течение их движения от Земли сквозь слой, где этот ток полагается существующим. При указанных параметрах вертикальная скорость частиц может быть оценена как j s / ( eN ₊ ) = 5 м / с , и значит время пролета сквозь слой примерно соответствует времени компенсации заряда, но как уже отмечалось, столь быстрое диффузионное вертикальное движение является нереальным.

Необходимо напомнить о существовании еще одного более простого объяснения наблюдаемых в приземном слое атмосферы вариаций вертикального электрического поля – за счет изменения проводимости воздуха. При этом не требуются какие-либо подземные электрические генераторы, которые в отсутствие разности потенциалов Земля–ионосфера фактически описываются граничным условием (3), и поэтому являются причиной явлений в нашей модели, как и в [Grimalsky et al., 2003; Pulinets et al, 2003]. При наличии обычной разности потенциалов между Землей и ионосферой около 300 кВ изменение проводимости приводит к изменению токов и полей, которые можно получить, решая уравнение электропроводности (1) с фиксированными значениями потенциала на верхней и нижней границах атмосферы. Если изменения проводимости не очень велики, и возмущением горизонтального электрического поля в ионосфере пренебречь, более общий подход не требуется. Как показано в [Ampferer et al., 2010], можно ограничиться одномерной моделью, если горизонтальный масштаб явления не менее 100 км.

Именно такой упрощенный подход использован в работе [Harrison et al., 2010]. В этой статье приведены зависимости проводимости от наличия радона и аэрозолей. Так, десятикратное увеличение концентрации радона приводит к росту проводимости и уменьшает E z в приземном слое атмосферы втрое, а десятикратное увеличение концентрации аэрозольных частиц с радиусом 0.25 мкм уменьшает проводимость и увеличивает это поле вчетверо. Соответствующие вариации E z составляют +70 В/м и –400 В/м. Поскольку проводимость всегда остается положительной, этот эффект не может изменить знак E z , но вариации E z могут быть любого знака и весьма велики. Например, большая положительная вариация E z может быть, если сильно уменьшить загрязнение воздуха.

Однако выводы о существенном влиянии этого эффекта на ионосферу, сделанные на основе таких оценок в работе [Harrison et al., 2010], представляются слишком смелыми, поскольку без обоснования подразумевается совпадение масштабов возмущения токовой скорости электронов в D-слое ионосферы и скорости перемещения профиля ионизации D-слоя, а эти скорости могут сильно различаться, так как ушедшие вверх электроны замещаются приносимыми снизу, и идут сложные процессы ионизации и рекомбинации. Следует также учесть, что эффект будет значительно слабее, есть горизонтальный размер области выброса радона или аэрозоля меньше 100 км, поскольку задача электропроводности атмосферы перестает быть одномерной, и изменение полного тока в небольшой области вблизи Земли в нижней ионосфре перераспределяется по гораздо более широкой области. При решении аналогичной теряющей одномерность задачи о проникновении токов от Земли в ионосферу в работе [Ampferer et al., 2010] показано, что при уменьшении до 10 км ширины областей положительного и отрицательного направления вертикального тока вблизи поверхности земли основная часть тока замыкается в нижней атмосфере, и доля этого тока, замыкающаяся через ионосферу, снижается до менее чем одной десятой с существенным увеличением горизонтального размера областей втекания и вытекания тока. Соответственно, в десятки раз уменьшаются токовые скорости электронов в D-слое по сравнению со значениями из одномерных оценок.

Работа [Harrison et al., 2010] является примером поиска механизмов ионосферно-литосферных связей без проникновения генерируемого в литосфере электрического поля в ионосферу. Обзор других физических механизмов таких связей дан в [Molchanov, Hayakawa, 2008].

Заключение

Таким образом, нами предложена новая математическая модель для описания квазистационарных атмосферных электрических полей с приближен- ным, но достаточно точным учетом проводимости ионосферы.

Показано, что две известные модели проникновения электрического поля от поверхности Земли в ионосферу [Grimalsky et al., 2003; Pulinets et al, 2003] приходится считать неудовлетворительными, хотя в атмосфере ниже 80 и 50 км соответственно они дают хорошие результаты. В этих моделях за счет произвольной постановки граничного условия фактически добавлен несуществующий проводник или, наоборот, исключен существующий хороший проводник. Поэтому не удивительно, что наше моделирование [Ampferer et al., 2010; Denisenko et al., 2008b] дает не такие большие ионосферные электрические поля, как [Pulinets et al, 2003], но и не такие малые, как [Grimalsky et al., 2003]. Модель [Сорокин, Чмырев, 2002], в рамках которой за счет добавления сторонних токов получается проникновение в ионосферу электрического поля до 8 мВ/м, неадекватна по указанным выше причинам.

Мы полагаем обоснованной оценку характерного ионосферного поля на уровне 0.1 мкВ/м. Оно создается в ночной тоносфере вертикальным электрическим полем 100 В/м вблизи Земли при горизонтальном масштабе явления x 0 =100 км, когда ширина областей с положительным и отрицательным знаками вертикальной компоненты поля составляет 314 км. Если области с вертикальным полем одного знака увеличивать, то поле в ионосфере пропорционально возрастет, но вряд ли области могут быть намного шире. Ионосферное поле также прямо пропорционально проводимости приземного воздуха, которая, по данным справочника [Campen et al., 1960], может быть на порядок больше использованного здесь значения 2∙10^–14 См/м, и, естественно, пропорционально напряженности вертикального поля вблизи Земли, которая в экстремальных случаях тоже может быть на порядок больше. За счет увеличения каждого из указанных двух параметров на порядок модельное поле в ионосфере можно увеличить во сто раз, до 0.01 мВ/м, но и в таком экстремальном случае оно все же остается на два порядка меньшим, чем можно было бы обнаружить, поскольку в ионосфере всегда присутствуют поля напряженностью несколько мВ/м. Следует также отметить отсутствие свидетельств в пользу одновременного увеличения проводимости и вертикального поля вблизи Земли, а если их произведение сохраняется, то почти не меняется и поле в ионосфере.

Особый интерес представляют области выброса газов, и в особенности радона, который дополнительно ионизирует воздух и тем самым увеличивает проводимость. При этом проникающее в ионосферу поле в нашей модели увеличивается, но для этого выброс должен происходить во всей области, занимаемой приземным полем одного знака, и без уменьшения напряженности этого поля. Для количественного анализа не хватает одновременных и распределенных измерений всех существенных параметров.

В дневное время модельное поле уменьшается в десятки раз обратно пропорционально увеличению интегральной педерсеновской проводимости ионосферы. К уменьшению приводит и наклон магнитного поля – оценки даны в [Denisenko et al., 2008b].

Основным ограничением для реализованного в настоящее время варианта нашей модели [Ampferer et al., 2010; Denisenko et al., 2008b] является возможная вертикальность магнитного поля и горизонтальной однородности ионосферы. Однако и в общем случае целесообразно использовать двумерную модель ионосферного проводника вида (6), наша версия которой представлена в статьях [Денисенко, 2002; Denisenko et al., 2008a].

Работа выполнена при поддержке РФФИ, проект 09-06-91000. Авторы благодарны А.А. Намгаладзе за содержательное, хотя и не приведшее к консенсусу обсуждение работы, а также коллегам из Института космических исследований Австрийской академии наук, совместно с которыми выполняется этот цикл исследований.