Простой метод оценки трудности учебных тестовых заданий

Проблема исчисления трудности учебных тестовых заданий имеет несколько важных и недостаточно исследованных аспектов. Известны два подхода к решению данной проблемы. Первый опирается на возможность оценки трудности задания, основываясь на его сложности и привлекая некоторые когнитивные характеристики, определение которых является самостоятельной задачей (А. Н. Колмогоров, Р. А. Гильманов). При этом под сложностью понимается минимальная длина алгоритма решения (по А. Н. Колмогорову) либо количество операций в неоптимизирован-ных алгоритмах.

Второй подход можно назвать успеш-ностным или сравнительным. Он предполагает, что трудность учебного тестового задания вводится через отношение числа учащихся, не решивших задачу, к общему количеству решавших ее (T ~ ~ Nh / N0). Этот подход часто используется в системах психологической, социологической и педагогической диагностики и предусматривает несколько видов статистических моделей в рамках «математической теории тестирования» (IRT). В моделях IRT вероятность того, что задание будет выполнено правильно, называется функцией успеха. Не вдаваясь в тонкости распространенных статистических моделей, отметим их главную для нас особенность, которая заключается в том, что модели предназначены для условий выбора ответа, а не для исчисления трудности заданий по математике, физике, химии и др. По поводу ограничений моделей IRT А. П. Попов высказывает следующее мнение: «Оценка уровня подготовленности испытуемых в модели Раша зависит лишь от общего числа правильно выполненных заданий, но не от их трудности»; «В модели Бирнбаума оценка уровня подготовленности испытуемого зависит лишь от суммарной дифференцирующей способности правильно выполненных заданий, но никак не связана с их трудностью»; «Ни о каком сравнении этих моделей с эмпирическими данными также не может быть и речи»; «Настало время признать ошибочность пути, по которому пошло развитие теории тестирования под влиянием работ Раша и Бирнбаума»; «Необходимы свежие идеи и новые подходы к решению задач, связанных с объективизацией оценки трудности тестовых заданий и уровня подготовленности испытуемых» [11]. Однако имеются и противоположные мнения. Одно из них принадлежит В. С. Аванесову: «IRT хорошо использовать для экспертизы теста и тестовых заданий, для оценки соответствия уровня трудности задания уровню подготовленности испытуемых» [1].

Необходимо отметить, что исследователи проблемы трудности учебных тестовых заданий выбирают в качестве предмета главным образом решение задач. Что касается условий задач, то результативность исследований в данном направлении, на наш взгляд, крайне мала. Под сложностью решения задачи часто понимается количество операций, а также некоторое их качество(свернутость), фиксирующееся, например, в терминах явных или неявных связей. Трудность решения считается субъективной характеристикой. При этом понятие субъективности иногда носит неопределенный смысл и распространяется на широкий спектр индивидуальных особенностей учащихся.

Согласно концепции А. Н. Колмогорова сложность — это длина наиболее короткого, рационального алгоритма решения задачи, в который следует включить и кратчайший путь понимания условия; трудность — это длина алгоритма с учетом некоторых когнитивных параметров [7].

Р. А. Гильманов считает трудность учебного тестового задания его объективной характеристикой, поскольку она «вызывается объективными закономерностями механизма мыслительной деятельности» [3]. В отличие от Р. А. Гильманова В. П. Мизинцев определяет трудность задачи как латентную характеристику [10].

Признавая необходимость дифференциации учебных задач по трудности, ряд исследователей тем не менее акцентируют свое внимание на сложности задачи. По мнению Г. А. Балла, сложность задачи оценивается количеством операций [2, с. 121]. И. Я. Лернер выделяет три фактора сложности задачи, для каждого из которых ученый устанавливает три качественных уровня [9]. Главным в оценке сложности при этом является количество операций, что сближает подход И. Я. Лернера с подходом Г. А. Балла.

Л. Г. Соколова выявляет шесть факторов сложности [13]. Некоторые факторы также предполагают то или иное количество операций. С позиций количества операций подходят к исчислению сложности и другие авторы. Например, О. Б. Епишева и В. И. Крупич в сложность решения математической задачи включают наряду с количеством элементов (отношений вида с = ab) виды связей, предполагающих также количество связывающих операций [6]. При этом авторы оценивают сложность по формуле S = m + n + l, где m — число основных отношений; n — число явных связей; l — число видов связей (явных или неявных). В задачах средней сложности величины m, n и l могут принимать, в частности, следующие значения: m = 2, n = 1, l = 1. Вычисляем: S = 4. Разрешение шкалы сложности (разрешение метода) е может быть оценено исходя из минимального вклада переменных, входящих в правую часть равенства, для вычисления сложности. Этот вклад равен единице (AS = 1). Тогда е = AS/S = 1/4. Значение е, выраженное в процентах, будет равно 25 %. Как видим, разрешение метода невелико.

В методе Н. Г. Рыженко и др. сложность рассчитывается как суперпозиция вершин и дуг графа, отображающего структуру решения задачи [12]. Разрешение шкалы сложности равно отношению минимальной сложности вершины к суммарной сложности графа и приблизительно равно разрешению метода, предложенного О. Б. Епишевой и В. И. Кру-пич.

В работах последнего десятилетия отмечаются попытки уйти от проблемы трудности и ограничиться сложностью учебных задач, используемых в качестве тестовых заданий. Так, по мнению В. В. Гузеева, «сложность — это объективная характеристика задачи, которая определяется структурой процесса поиска решения»; «трудность задачи является субъективной характеристикой, т. е. зависит от того, кто решает эту задачу...» [4, с. 51, 54]. Некоторые ученые данные понятия вообще не различают. Например, В. М. Кротов утверждает, что «во многих сборниках задач по физике содержатся задачи разной сложности (трудности)» [8].

Для оценки трудности учебных тестовых заданий нами на первый план выдвигается гипотеза о возможности использования субъект-предикатного подхода к анализу содержания задач. Данный подход представляется эффективным в силу разработанности его собственных когнитивных и логических оснований. Для нахождения структуры содержания условия и решения учебной задачи мы в значительной степени ориентируемся на логику Л. П. Доблаева, утверждающего, что структуру содержания текста можно представить в виде иерархии текстовых субъектов как систему модификации основного, самого широкого по содержанию, субъекта [5].

С целью наглядного изображения субъект-предикатной структуры условия задачи и ее решения удобно использовать графологические модели.

В наших рассуждениях мы опираемся также на «экспертный» подход А. Н. Колмогорова, о котором упоминалось выше. В процессе решения задачи эксперт использует самые лаконичные алгоритмы получения эффективной гипотезы решения (обработки условия) и собственно решения, что сводится к раскрытию главного текстового субъекта, в роли которого выступает искомая величина. Мы объективируем таким образом трудность тестового задания, постулируя минимальные значения сложности условия и решения и вводя коэффициенты трудности, учитывающие, в частности, место модификатов (текстовых субъектов) в их иерархии. Другим параметром, объективирующим трудность задачи, является критерий модифицируемости текстового субъекта, отражающий количество непосредственных модифи-катов.

Итак, трудность учебного тестового задания, оставаясь, по сути, когнитивной характеристикой, может быть эффективно формализована посредством учета минимального набора параметров. Данное обстоятельство позволяет создать эффективную шкалу трудности школьных и вузовских задач по ряду естественно-научных и математических дисциплин.

К отличительным особенностям предлагаемого нами метода следует отнести прежде всего высокое разрешение шкалы трудности учебных тестовых заданий, которая, как мы увидим ниже, может составлять единицы процентов для задач среднего диапазона трудности.

Для иллюстрации предлагаемого метода рассмотрим типовую учебную задачу по физике.

3 а д а ч а. Стальной осколок, падая с высоты 500 м, имеет у поверхности Земли скорость 50 м/с. Насколько повысится температура осколка, если считать, что вся работа сопротивления воздуха пошла на его нагревание?

Из известного выражения Q = стАТ определяем неизвестную величину АТ, играющую роль главного текстового субъекта: АТ = Q/ст. Правая часть полученного равенства есть предикат, состоящий из субъектов Q и ст. Из данных двух субъектов модификации подвергается лишь субъект Q.

Q = A = АЕ = Е_п - Е_кили Q = Е_п - Е_к , где Е_п = mgh, Е_к = ти ²/2.

Граф структуры решения задачи показан на рисунке.

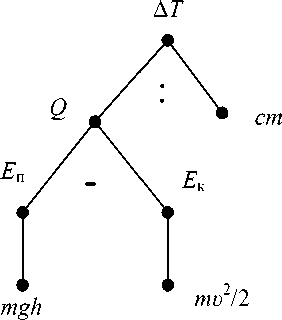
Граф субъект-предикатной структуры решения задачи:

АТ — главный субъект (искомая величина)

Субъекты cm, mgh и ти ²/2 далее не подвергаются модификации и потому называются терминальными. Они формируют выражение для вычисления АТ:

АТ = (mgh - т и ²/2)/ст.

Для учета степени модифицируемости субъектов зададим для каждого субъекта коэффициент модифицируемости q следующим образом. Если субъект далее не модифицируется, то q = 1. Если субъект модифицируется, то для каждого непосредственного модификата q = 2. Следовательно, для субъекта Q q = 4, поскольку данный субъект модифицирован в два субъекта (таблица). Его непосредственными модификатами являются Е_п и Е_к. Для субъектов же Е_пи Е_к q = 2 (для каждого), поскольку они оба далее модифицируются в один субъект.

Другой трудно стной характеристикой, как мы уже говорили, является коэффициент иерархичности, величину которого мы определим следующим образом. Для терминальных субъектов ст, mgh и mu2/2 коэффициент иерархичности равен 1, для субъектов Е и Е — 2, для субъекта Q — 3 (см. таблицу). Как видим, минимальное значение коэффициента иерар хичности имеют терминальные субъекты, а каждая последующая ступень в иерархии субъектов увеличивает его значение на единицу.

Трудностные характеристики субъектов

Субъект Коэффициент модифицируемости Коэффициент иерархичности модификации Т0 Исходная трудность субъекта T Трудность определения cm                    11

mgh                 11

mu2/2                    11

Q                 43

Е                22

Еп                 22

к

Трудность определения (или просто трудность) любого субъекта равна произведению исходной трудности (Т 0 = 1) на значения коэффициентов иерархичности и модифицируемости. Следовательно, трудность терминальных субъектов всегда равна Т₀ = 1.

Результирующая трудность решения задачи Т будет равна сумме значений трудности определения всех субъектов, приведенных в таблице. Как можно видеть из таблицы, Т = 23. Разрешение метода равно Т 0 /Т. В нашем случае это отношение, выраженное в процентах, приблизительно равно 4 %. Данная величина, что вполне естественно, зависит от абсолютного значения трудности задачи Т и составляет для Т = 70 около 1,5 %.

В дидактике высказываются противоположные мнения относительно проблемы трудности условия задачи. Современный учебный тестинг предлагает формулировать условие таким образом, чтобы оно было максимально понятным для учащихся. С другой стороны, существует точка зрения на трудность задачи, когда трудность относится не к решению задачи, а к ее условию. Например, о необходимости наименьшей определенности в текстах задач при их постановке говорил П. Л. Капица. Он отмечал, что именно при таком подходе к постановке задач можно воспитывать самостоятельное творческое мышление учащихся. Однако в современной школе «кроссвордный» способ формулирования условия задачи «по Капице» часто при-

1 1 1 1 11 1 12 1 4 1 4

водит к отказу учащихся от решения задачи, что говорит о серьезной демотивирующей силе этого метода.

Поясним сказанное следующим примером. Имеется две формулировки одной и той же задачи. Первая представляет собой оригинал условия, принадлежащего автору, вторая предложена профессором Омского государственного педагогического университета В. А. Да-лингером.

Таким образом, экспертное решение задачи — это раскрытие главного субъекта самым лаконичным способом. Что же касается условия, то для исчис- ления его трудности необходим также рациональный способ «выхода» на главный текстовый субъект, в качестве которого выступает неизвестная величина. Общую трудность задачи можно вычислить как сумму трудностей условия и решения, причем и то и другое является экспертным, наиболее рациональным конструктом.

СПИСОК

ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

• 1.    Аванесов, В. С. Основные понятия и положения математической теории измерений (item response theory) [Электронный ресурс] / В. С. Аванесов. — Режим доступа: http:// testolog.narod.ru/theory 60.html.

• 2.    Балл, Г. А. Теория учебных задач: психолого-педагогический аспект / Г. А. Балл. — М. : Педагогика, 1990. — 184 с.

• 3.    Гильманов, Р А. Измерение трудности учебных упражнений посредством моделирования процесса их выполнения : дис. ... канд. пед. наук / Р А. Гильманов. — Казань, 1987.

• 4.    Гузеев, В. В. Соотнесение сложности и трудности учебных задач с уровнями планируемых результатов обучения / В. В. Гузеев // Шк. технологии. — 2003. — № 3. — С. 50—56.

• 5.    Доблаев, Л. П. Смысловая структура учебного текста и проблемы его понимания / Л. П. Доблаев. — М. : Педагогика, 1982. — 176 с.

• 6.    Епишева, О. Б. Учить школьников учиться математике: Формирование приемов учебной деятельности : кн. для учителя / О. Б. Епишева, В. И. Крупич. — М. : Просвещение, 1990. — 128 с.

• 7.    Колмогоров, А. Н. Теория информации и теория алгоритмов / А. Н. Колмогоров. — М. : Наука, 1987. — 304 с.

• 8.    Кротов, В. М. К вопросу о сложности (трудности) физических задач / В. М. Кротов // Фiзiка: праблемы выкладання. — 1999. — № 3. — С. 69— 74.

• 9.    Лернер, И. Я. Факторы сложности познавательных задач / И. Я. Лернер // Новые исследования в педагогических науках. — М., 1970. — Вып. 14. — С. 86—91.

• 10.    Мизинцев, В. П. Информационный анализ показателя сложности и трудности учебной задачи / В. П. Мизинцев // Вопросы преподавания физики в высшей школе. — Хабаровск, 1976. — С. 132—186.

• 11.    Попов, А. П. Критический анализ параметрических моделей Раша и Бирнбаума / А. П. Попов // Материалы 4-й науч.-метод. конф. «Инновационные методы и средства оценки качества образования». — М., 2006. — С. 231—235.

• 12.    Рыженко, Н. Г. Структуризация и систематизация сюжетных задач по сложности их решения / Н. Г. Рыженко, Н. А. Жигачева // Вести. Омск. ун-та. — Омск, 1998. — № 4. — С. 111—114.

• 13.    Соколова, Л. Г. О формировании у студентов физического факультета умений обучать учащихся решению задач / Л. Г. Соколова // Современные психолого-педагогические проблемы высшей школы. — Л., 1973. — Вып. 1. — С. 62.

Поступила 23.10.09.