Противоречия и классификация

Способ задания предикатов видимости ограничен условием, согласно которому все грани меньшей размерности, принадлежащие видимой грани, также должны быть видимы. Наиболее удобно поэтому индуктивное задание этих предикатов, начиная с предиката видимости вершины.

Пусть пространства L , L ₁, L ₂ имеют конечную размерность и имеются разложения вершин по граням.

Покажем, что в этом случае возможна аппроксимация системы (1) системой линейных неравенств.

Пусть q — некоторая вершина, х — ее проекция и Т(х) — множество проекций граней т = _х 1 ... _х^$, ее содержащих, т.е. удовлетворяющих условию

s ( T ) ^х = ^ ^а j ^{( т} ) ^{х ;}

j = 1

s ( T )

Q j ^ o ( V j G 1’ s ( т )), £ _Q j (т ) = 1.

j = 1

Тогда вершину q можно считать видимой, если              _{s ( T )}

У х < £ Q ( т ) УхЧ ^ т G T ( х )).

j = 1

Эта система неравенств линейна по системе переменных у = [ у_х G L 2 : х G M ]. Способы задания предикатов видимости граней более высокого порядка определяются классом допустимых интерпретаций.

Рассмотрим подробнее задачу восстановления трехмерного многогранника по его плоской проекции.

Пусть имеется некий трехмерный многогранник Q , определяемый множеством его вершин M_Q, ребер M _Q² и граней M _Q ³ .

Известна проекция Р этого многогранника на некоторую плоскость, задаваемую вектором нормали l . Требуется по известной проекции восстановить исходный много-

Мазуров Вл.Д., Смирнов А.И.

гранник с точностью до некоторого отношения эквивалентности, которое будет определено ниже.

Восстановленный многогранник будем называть интерпретацией его проекции.

Та же терминология будет употребляться и для его составных частей: вершин, ребер, граней. Проекции вершин (составляющие множество M _p ), ребер (множество M_p ² ) и граней (множество M ³ _p) исходного многогранника Q будем также называть вершинами, ребрами и гранями соответственно.

Введем на плоскости проекции систему координат x ₁, x ₂ . Третью координату у направим вдоль вектора l . Таким образом, каждой вершине многогранника Q соответствует вершина р = (x ₁, x ₂ ) фигуры Р.

Определим на множестве прообразов фигуры Р отношение эквивалентности и будем считать задачу реконструкции решенной, если будут найдены представители всех классов эквивалентности.

Введем на множестве граней M _Q³ многогранника Q частичный порядок. Будем считать, что грань Г ₁ предшествует грани Г ₂, если существует точка х = (x ₁, x ₂ ), принадлежащая пересечению 7 1 П 7 2 проекций 7 1 и 7 2 этих граней, имеющая прообразы z = ( X i , x 2 , y j и z 2 = ( X i , x 2 , y 2 ) на гранях Г ₁ и Г ₂ соответственно, причем У 1 <  y 2 ^.

Для того, чтобы введенное отношение было частичным порядком, достаточно предположить, что

• (В1)    многогранник Q - выпуклый.

В дальнейшем будем считать это требование выполненным. Нетрудно проверить, что в этом случае определение частичного порядка корректно и не зависит от выбора точки х из пересечения проекций граней.

В соответствии с естественной интерпре- тацией будем называть минимальные элементы множества MQ3 «видимыми гранями». Многогранники, у которых грани, имеющие одну и ту же грань-проекцию, одновременно видимы или невидимы, будем считать эквивалентными.

Таким образом, задачу можно уточнить следующим образом: восстановить исходный многогранник с точностью до набора видимых граней.

Будем предполагать также выполненным условие

• (B2)    вершины многогранника Q находятся в общем положении.

Условия (Bl), (B2) гарантируют «невырожденность» многогранника Q, положительность его объема.

Из условий (В1) и (В2) получаем также следствие

• (B3)    если видима часть грани, то и вся грань целиком видима.

Заметим, что в этих условиях существует покрытие многогранника со M _p гранями. Поэтому исходная задача эквивалентна задаче нахождения минимальных (по включению) покрытий многогранника со M _p . Это обстоятельство дает один из возможных подходов к решению исходной задачи.

Но перспективнее по ряду причин представляется предложенный подход, основанный на аппроксимации понятия видимости граней системами линейных неравенств.

Заметим, что в принципе этот подход не ограничивается выпуклыми многогранниками; этот случай взят для простоты рассмотрения.

Заметим также, что во всех интерпретациях ребра, принадлежащие границе многогранника со M _p , будут видимы.

Далее, из видимости граней большей размерности (ребер, граней в трехмерном случае) следует видимость граней меньшей размерности, ее составляющих (вершин, ребер соответственно). Обратное утверждение в общем случае неверно, но и оно спра- ведливо, если не все составляющие грани меньшей размерности принадлежат границе д(со Mp ) многогранника со Mp и вы- полнено условие

• (B4)    объединение любого числа граней не является гранью.

Перед решением задачи полезно проверить выполнение некоторых простых условий, вытекающих из наших требований, типа соотношения Эйлера:

|M _p | — M , 21 + | m p | = 2 , и того факта, что из каждой вершины должны исходить как минимум три ребра.

Перейдем к интерпретации вершин. Пусть p Е М _p. Если p е8 (соМ _p), то эта вершина видима в любой интерпретации.

Пусть p е 'nt(coMp). Тогда существует грань pi ,..., pi , ее содержащая. Находим разложение kk p = £ »jfij, aj > 0(Vj Е 1, k), £ aj = 1.

j = 1        ^J                                 j = 1

Если pj = (x 'j, x2'j), qj = (x 'j, x2'j, yj), p = (x1, x2), q = (x1, x 2, y), то вершину q считаем видимой, если

k y <^ ajyj.

= 1

Перейдем к вопросу об интерпретации ребер. Итак, пусть имеется ребро p ₁ p ₂ Е М²_р

Как замечено ранее, видимости вершин (если хоть одна из них не лежит на границе со M_p ) достаточно для видимости ребра.

Но метод интерпретации проекций, основанный на интерпретации вершин, не гарантирует для полученного многогранника выполнение перечисленных условий; класс интерпретаций в этом случае слишком широк и содержит различные «вычурные» фигуры. Поэтому мы будем пользоваться следующим усилением метода интерпретации вершин. p1 = (x, x2), p2 = (x2, x2), Пусть qi    (xi , x 2, yi), q 2 (xi , x 2, y 2).

Найдем все грани ri = p‘i...p‘k (i Е1,r), которые ребро p1 p2 пересекает. Находим разложения ki                         ki fl =^a!spS , p2 =^a2spS, s=1                  s=1

ki

£ a s = 1 ( t = 1,2).

s = 1

Далее, считаем, что ребро q1q2 видимо тогда и только тогда, когда выполнены следующие неравенства:

k i

У1 <£ «i'syis, s=1

ki y 2 <£ a 2sys('Е1 r )• s=1

Получим подобные системы для всех ре- бер из Mp2 и объединим в одну:

^ ₁ y <  0;

A_ny <  0.

Здесь n = | M p 2| ; у — вектор, составленный из всех полученных переменных y ₁ , y ₂ , y _i (его размерность равна | М_Р |).

Необходимо учесть также отсутствие «изгибов» граней с числом вершин более трех. Это дает систему равенств (возможно, пустую) вида

Ву = 0, (5)

позволяющую снизить размерность системы (9). В итоге получаем систему нера- венств

A 1 y <  0;

A n y <  ⁰,

Мазуров Вл.Д., Смирнов А.И.

где вектор y содержит лишь часть переменных вектора у.

Теперь осталось найти все МСП системы (6) и выбрать из них те, которые достаточны для интерпретации ребер, т.е. цели ком составлены из некоторых матриц Ai .

Для интерпретации граней будем пользоваться сделанным замечанием, т.е. проведем ее, исходя из интерпретации ребер.

Рассмотрим известный пример [9] противоречивого изображения, т.н. «куб Нек-кера» (рис.1).

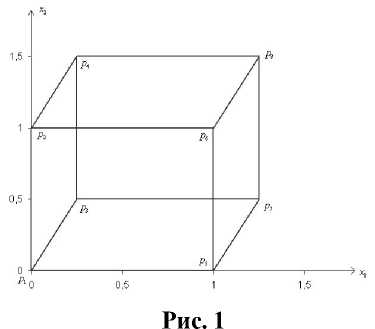
Здесь M p = { P i , p 2 ,..., p 8 } , где

P i = (0,0); p 2 = (0,i); p 3 = 4,2 ^j ; p 4 = 4^,| ^j ; P 5 = (1,0); p ₆ = (1,1); p 7 =| 4,2 j ; p 8 =[ 4,2 j .

Множество ребер имеет вид

M P = { P 1 P 2 , Р 1 Р з , P 1 P 5 , P 2 P 4 , P 2 P 6 , Р з P 4 , Р з P 7 , P 4 P 8 , P 5 P 6 , P 5 P 7 , P 6 P 8 , P 7 P 8 } , где M pp | = 12.

Каждой точке p _z = ( x j , x 2 ) соответствует вершина q _z = ( x 1¹ , x 2¹ , у₄ ) многогранника в трехмерном пространстве.

Заметим, что ребра p1p2,p2p4,p4p8,p7p8,p5p7,p1p5

всегда видимы (при любой интерпретации).

Составим систему уравнений относительно вектора у = [ у 1 ,у 2 ,..., у 8 ] , вытекающую из факта отсутствия «изгибов» граней

• 1)    q^ е q2 q5 q6 ^ у 1 - у 2 - у5 + у 6 = 0;

• 2)    q 5е q 6 q 7 q8 ^ у 5- у 6- у 7 + у8 = 0;

• 3)    q 3е q4 q 7 q 8 ^ уз - у 4- у 7 + у 8 = 0;

• 4)    qе q 2 q з q 4 ^ у1 - у 2- уз + у 4 = 0;

• 5)    qе q 3 q 5 q 7 ^ у 1- уз - у 5 + у 7 = 0;

• 6)    q2 е q4q7 q8 ^ у3 - у4 - у7 + у8 = 0. _

Эта система эквивалентна следующей выражающей переменные y4 , y6 , y7 , y8 че- рез y1, y2, y3, y5 :

• у 4 = у 1 + у 2 + у з ;

• у 6 = ^- у 1 + у 2 +      у 5 ;

• ^у 7 = ^{- у} 1 +      ^у 3 + ^у 5 ;

• у8 = - 2у1 + у2 + у3 + у5. .

Перейдем к составлению системы неравенств, отражающей факт видимости соответствующих ребер многогранника.

Внутри многогранника со M_p лежат ребра p ₁ p ₃, p ₂ p ₆, p ₃ p ₄, p ₃ p ₇, p ₅ p ₆, p ₆ p ₈ . Следовательно, только те ребра, которые им соответствуют, могут «заслоняться» другими гранями и быть невидимыми в некоторых интерпретациях.

• 1)    Ребро q ₁ q ₃ может «заслоняться» только гранью q ₁ q ₂ q ₆ q ₅ . Отсюда единственное неравенство, вытекающее из соотношения 111

Р з = 4 Р 1 ⁺ 2 Р 2 ⁺ 4 Р 5 ;

• ⁽¹⁾    у з <  4 у 1 ⁺ 2 у 2 ⁺ 4 у 5 .

• 2)    Ребро q ₂ q ₆ может «заслоняться» гранями q ₁ q ₂ q ₄ q ₃ и q ₃ q ₄ q ₈ q ₇ . Поскольку вершина q ₂ всегда видима, в первом случае достаточно написать неравенство, вытекающее из невозможности пересечения ребер и граней, а именно, точка q ₆ должна быть

«впереди» плоскости - продолжения грани q 1 q 2 q 4 q 3 .

Из соотношения р 6 = — 2 р 1 — р ₂ + 4 р 3 получаем

• ⁽²⁾    y 6 < ^{— 2} y 1 ^— y 2 ^{+ 4} y 3 .

Во втором случае, когда рассматривается грань q ₃ q ₄ q ₈ q ₇ , из соотношений

5  13   111

P 2 = 4 P 4 ⁺ 2 P 7 ^— 4 P 8 , P 6 = 4 P 4 ⁺ 2 P 7 ⁺ 4 P 8

аналогично получаем еще два неравен- ства:                 5       13

• ⁽³⁾    У 2 <  4 У 4 ⁺ 2 У 7 ^— 4 У 8 ;

• ⁽⁴⁾    У 6 <  4 У 4 ⁺ 2 У 7 ⁺ 4 У 8 .

Далее более кратко будем записывать лишь рассматриваемые ребра, грани, соотношения и соответствующие неравенства.

• 3)    Ребро q ₃ q ₄ . Грани q ₁ q ₂ q ₆ q ₅ и q ₂ q ₄ q ₈ q ₆.

Соотношения:

P 3 = Z P 1 ⁺ ?P 2 ⁺4 P 5 ;

3   31    3     1

p 4 = ^— 4 P i ⁺ 2 p 2 ⁺ 4 p 5 ; p 3 = 2 p 2 ^— p 4 ⁺ 2 p 6 -

Неравенства:

• ⁽⁵⁾    = ⁽¹⁾ у 3 < 4 У 1 ⁺ 2 у 2 ⁺ 4 у 5 ;

3  31

• (6)     у 4 <— 4 У1 + 2 у 2+4 у 5;

• (7)      у 3 < 2 у 2 —у 4+2 у 6

• 4)    Ребро q ₃ q ₇ . Грани q ₁ q ₂ q ₆ q ₅и q ₂ q ₄ q ₈ q ₆.

Соотношения:

Р 3 = ¹ Р 1 ^{+ 1} Р 2 ^{+ 1} Р 5 ;

4  24

Р 3 = ² Р 5 ^{+ 2} Р 6 ^{— 3} Р 7 ; Р 7 =^— 4 Р 1 ⁺ 2 Р 2 ⁺ 4 Р 5 -

Неравенства:

• ⁽⁸⁾    =0) У 3 <  4 У , ⁺ 2 У 2 ⁺ 4 У 5 ;

• (⁹⁾       У 3 <  ² У 5 ^{+ 2} У 6 ^{— 3} У 7 ;

• (10)     у 7 <^— 4 У 1 ⁺ 2 у 2 ⁺ 4 у 5

• 5)    Ребро q ₅ q ₆ . Грани q ₁ q ₃ q ₇ q ₅ и q ₃ q ₄ q ₈ q ₇ .

Соотношения:

P 5 = 4 P 4 ⁺ ?Р 7 ' I P 8 ; ■

1   11     31

Р 6 = 4 Р 4 ⁺ 2 Р 7 ⁺ 4 Р 8 ; Р 6 =^— 2 Р 1 ^{+ 2} Р 3 ⁺ 2 Р 5 -

Неравенства:

• ⁽¹¹⁾        у 5 <  4 у 4 ⁺ 2 у 7 ^— 4 у 8 ;

• (12)    =(4) у6 <4у4+ 2у7+ 4у8;

• ⁽¹³⁾        у 6 <^— 2 У 1 ^{+ 2} у 3 ⁺ 2 у 5 -

• 6)    Ребро q6q8 . Грань q3q4q8q7 . Соотно-
• 1  11

шение p 6 = -p 4 ⁺ - p 7 ^—7 ^р 8 4  24

Неравенство

• ⁽¹⁴⁾    = ⁽⁴⁾ У 6 <  4 У 4 ⁺ 2 у 7 ⁺ 4 у 8 ;

Итак, имеем следующую систему неравенств:

• (1)    — У 1 — 2 У 2 + 4 У 3 — У 5 <  0;

• ^{(2)     2} У 1 + у 2 - ⁴ у 3 + у 6 <  0;

• (3)   4 У 2 — 5 У 4 — 2 У 7 + 3 У 8 <  0;

• ^{(4)    — y} 4 ^{+ 4 y} 6 ^{— 2 y} 7 ^{— y} 8 <  ^0;

• (5)    = (1)

• (6)    3 У 1 — 6 У 2 + 4 У 4 — У 5 <  0;

• (7)    — 3 у 2 + 2 у 3 + 2 у 4 — у 6 <  0;

• ⁽⁸⁾    = ⁽¹⁾;

• (9)    у 3 — 2 у 5 — 2 у 6 + 3 у 7 <  0;

• (10)    3 у 1 — 2 у 2 — 5 у 5 + 4 у 7 <  0;

• (11)    — У 4 + 4 У 5 — 6 у 7 + 3 у 8 <  0;

• (12)    = (4);

• (13)    3 y_Y — 4 у 3 — у 5 + 2 у 6 <  0;

• (14)    = (4)-

• Мазуров Вл.Д., Смирнов А.И.

Эта система, с учетом полученных выше равенств, выражающих неизвестные y ₄, y ₆, y ₇, y ₈ через остальные, превращается в следующую

(здесь h ( y ) = - y i - 2 y 2 + 4 y 3 - y 5 ):

• (1)    h <  0, (7) h <  0, (2) - h <  0, (9) h <  0, (3) - h <  0, (10) h <  0, (4) - h <  0, (11) - h <  0, (6) h <  0, (13) - h <  0.

  q ₁ q ₃ , q ₃ q ₄ , q ₃ q ₇ (рис. 2), второй — ребра

  
  
  

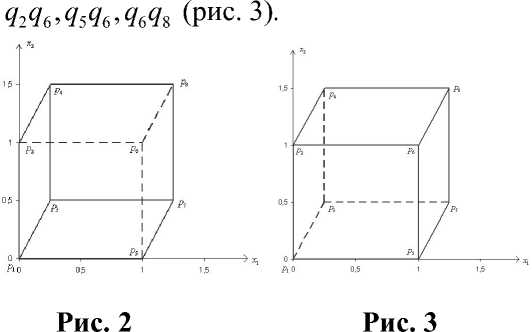
Последняя система имеет лишь две МСП:

МСП 1: (1), (6), (7), (9), (10);

МСП 2: (2), (3), (4), (11), (13).

Перечислим неравенства, справедливость которых необходима для видимости соответствующих ребер:

q 1 q 3 : (1); q 1 q 3 :(1),(9),(10); q 1 q 3 : (2), (3), (4);

q 1 q 3 :(4),(11),(13); q 1 q 3 : (1),(6), (7); q 1 q 3 :(4).

Таким образом, первой МСП соответствует интерпретация, где видимы ребра

Итак, первая интерпретация—видимы грани q ₁ q ₂ q ₄ q ₃, q ₃ q ₄ q ₈ q ₇, q ₁ q ₃ q ₇ q ₅. Вторая интерпретация — видимы грани q ₁ q ₂ q ₆ q ₅, q ₅ q ₆ q ₈ q ₇, q ₂ q ₄ q ₈ q ₆.

Таким образом, мы показали на этом классическом примере противоречивого изображения эффективность предложенного нами подхода на основе максимальных непротиворечивых подсистем (МСП) исходной противоречивой системы.