Проверка педагогической гипотезы о повышении рейтинговых характеристик студентов при введении в учебный процесс консультационных занятий в дистанционном формате

Наличие у сегодняшних студентов прочной теоретической и практической базы по фундаментальным дисциплинам, центральное место среди которых занимает математика, диктуется постоянно повышающимися требованиями к выпускникам ведущих технических вузов, в числе которых находится и ФГБОУ ВПО «Уфимский государственный нефтяной технический университет» (УГНТУ).

Констатируя тот факт, что отдельная часть выпускников школ не обладает достаточно высоким уровнем подготовки и особенно мотивацией к освоению учебных дисциплин [1, 2], можно прийти к осознанию необходимости применения качественно новых форм обучения, индивидуального подхода к каждому из учащихся, использование современных средств связи и мультимедии, т. е. подход, основанный на применении ИКТ [3]. Необходимость данных мероприятий диктуется и практикой сокращения аудиторных часов на консультации, т. е. смещения образовательного процесса из аудиторного в самостоятельную плоскость.

Потребность проводить консультирование студентов с использованием ИКТ возникла из необходимости каждодневно отвечать на вопросы после учебных занятий и вследствие ограниченности аудиторного времени как у студентов, так и у преподавателя.

В то же время, например, по электронной почте каждый студент может проконсультироваться у преподавателя по любому интересующему его учебному вопросу практически в режиме on-line. После выполнения и пере- дачи на проверку своих отчетных работ студент в личный почтовый ящик получает собственный рейтинг и рейтинг своего потока, определяющий положение студентов, согласно суммарному количеству баллов на текущий момент. Наглядность рейтинга вызывает чувство здорового учебного соперничества среди студентов потока [4]. Преимущества балльнорейтинговой системы с использованием информационно-коммуникационных технологий заключаются в гласности, открытости и доступности, унификации рабочих программ, регламентировании количества отчетных работ по дисциплине, каждодневном сотрудничестве преподавателя со студентами [5].

Данные обстоятельства позволили выдвинуть следующую педагогическую гипотезу исследования. Активное и целенаправленное введение педагогом в учебный процесс нового формата проведения консультаций учащихся в формате ИКТ (рис. 1, 2), с применением, например, широко распространенной и общедоступной системы Moodle позволяет вызвать положительную мотивацию учащихся к изучению учебного материала по дисциплине «Математика», количественным отображением повышения качества по которой служит повышение среднего значения группового рейтингового балла по данной дисциплине [6].

Исследование данной гипотезы проводилось с применением эффективных программных средств в области анализа данных – Statistica и Microsoft Office Excel, соответствующих мировым стандартам качества.

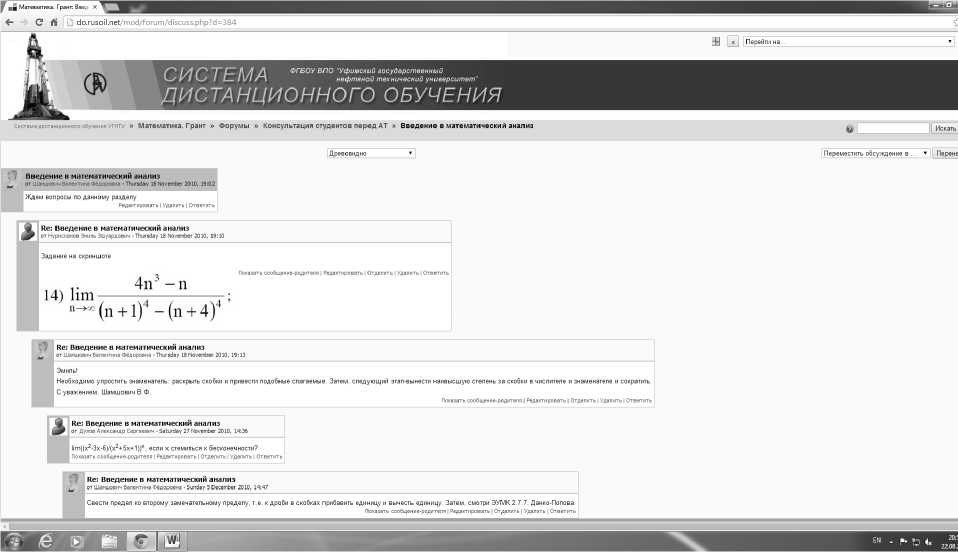
Рис. 1. Фрагмент консультационного диалога по математике по разделу «Введение в анализ» в образовательной среде Moodle

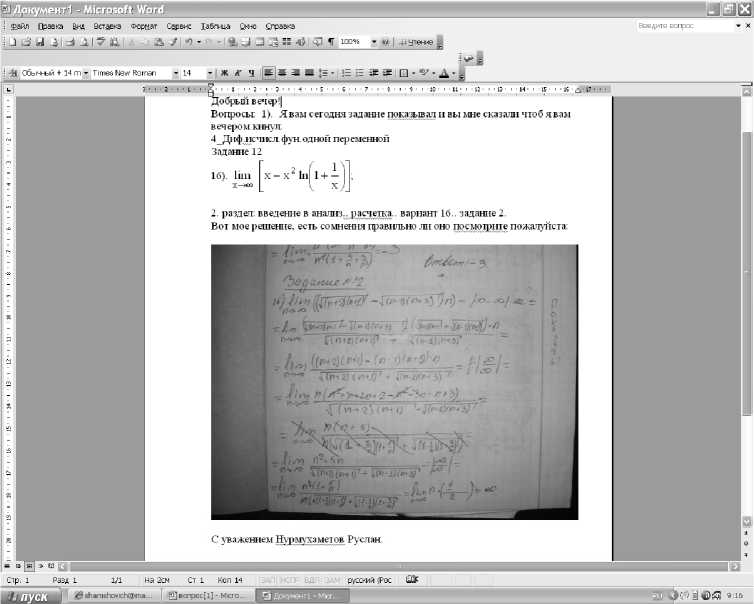
Рис. 2. Фрагмент консультационного диалога по математике по разделу «Введение в анализ» по электронной почте

На первом этапе была сформирована репрезентативная выборка студентов. Для этого случайным образом были отобраны по три группы учащихся I курса, как консультируе- мые с помощью ИКТ, так и консультируемые аудиторно по традиционной классической схеме. Таблица контрольных мероприятий приводится в табл. 1.

Таблица 1

Зачетная рейтинговая таблица за 1 семестр

Дата (уч. нед.)	Вид и наименование рейтинговой работы	Кол-во баллов	Макс. балл
Расчетные задания
	1) Расчетные задания № 1 (РЗ_1) Раздел № 1 «Линейная и векторная алгебра» УМК / Материалы для самостоятельной работы (РЗ с. 95–106). Раздел № 2 «Аналитическая геометрия» УМК / Материалы для самостоятельной работы (РЗ с. 98–112)		10
	2) Расчетные задания № 2 (РЗ_2) Раздел № 3 «Введение в математический анализ» УМК / Материалы для самостоятельной работы (РЗ с. 116–139). Раздел № 4 «Дифференциальное исчисление функции одной переменной» УМК / Материалы для самостоятельной работы (РЗ с. 97–119)		10
Лабораторные работы
	1) Лабораторная работа № 1 (ЛР_1) «Решение систем линейных уравнений методом Гаусса» УМК / Материалы для самостоятельной работы (ЛР с. 107–117)		5
	2) Лабораторная работа № 2 (ЛР_2) «Метод наименьших квадратов» УМК / Материалы для самостоятельной работы (ЛР с. 117–129)		5
Аттестационные тестирования
	1) Аттестационное тестирование № 1 (АТ_1) Контрольно-измерительные материалы для разделов № 1 «Линейная и векторная алгебра», № 2 «Аналитическая геометрия» УМК (КИМ)		35
	2) Аттестационное тестирование № 2 (АТ_2) Контрольно-измерительные материалы для разделов № 3 «Введение в математический анализ», № 4 «Дифференциальное исчисление функции одной переменной», № 5 «Дифференциальное исчисление функции нескольких переменных» УМК (КИМ)		35

Для проверки выдвинутой (нулевой) гипотезы используем двухвыборочный t-критерии Стьюдента, который определяет значимость различий средних в зависимых и независимых выборках при заданном уровне ошибки I рода, при условии нормальности их распределений в условиях равенства или неравенства групповых дисперсий [7].

Нормальность распределений индивидуальных рейтинговых баллов учащихся была проверена путем построения гистограмм с наложением на них кривой Гаусса с соответствующими параметрами. На рис. 3 приведен пример гистограммы для одной из контрольных группы МП-08-01.

На следующем этапе для обеспечения надежности и достоверности проводимых исследований произведем проверку учебных групп на однородность по средней величине группового рейтингового балла по двухвыборочному t-критерию Стьюдента, который определяет значимость различий средних в зависимых и независимых выборках при задан- ном уровне ошибки I рода, при условии нормальности их распределений.

В результате статистического анализа, выполняемого в надстройке пакетом анализа Microsoft Office Excel, вычислялось наблюдаемое значение t-критерия (t-статистика) и сравнивалось с критическими точками одностороннего и двустороннего критериев (табл. 2–3).

В обоих случаях выполнялось условие (Т набл = t-статистика)

I набл     двуст.крит , согласно которому при выбранном уровне значимости α = 0,05 (величина ошибки I рода) нет оснований отвергнуть нулевую гипотезу о равенстве средних значений рейтинговых баллов по учебным группам, консультируемых с помощью ИКТ. Таким образом, они являются однородными выборками с точки зрения равенства групповых средних.

Далее перейдем к анализу выборок предыдущих по году обучения учебных групп. В них также наблюдается соответствие

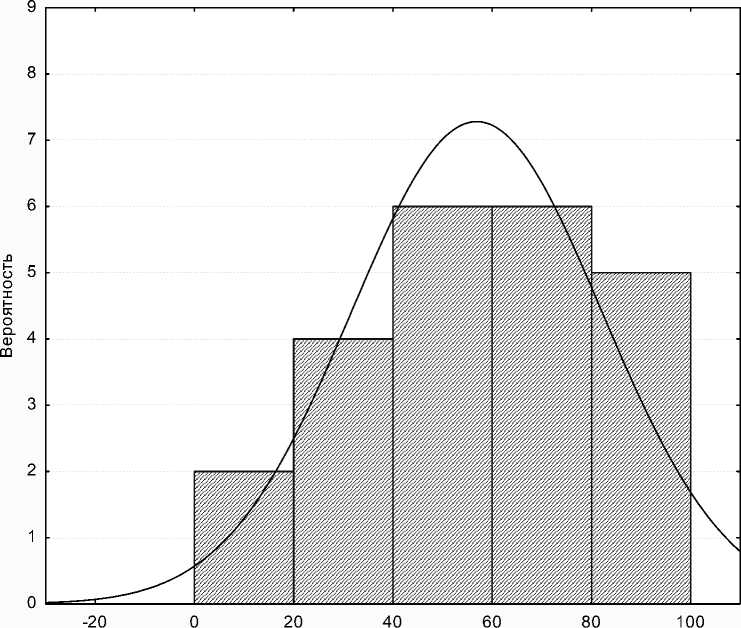
Величина рейтингового балла учащегося

Рис. 3. Гистограмма частот рейтинговых баллов группы МП-08-01

Таблица 2

Результаты двухвыборочного t-теста Стьюдента с различными дисперсиями для средних для учебных групп МП-08-01 и МП-08-02

Числовые характеристики	МП-08-01	МП-08-02
Среднее	56,88695652	57,61739
Дисперсия	635,3411858	684,9188
Наблюдения	23	23
t-статистика	–0,096408569
P(T<=t) одностороннее	0,461816938
t критическое одностороннее	1,680229977
P(T<=t) двухстороннее	0,923633875
t критическое двухстороннее	2,015367547

Таблица 3

Результаты двухвыборочного t-теста Стьюдента с различными дисперсиями для средних для учебных групп МП-08-02 и МП-08-03

Числовые характеристики МП-08-02 МП-08-03 Среднее 57,6173913 57,46957 Дисперсия 684,9187747 1068,179 Наблюдения 23 23 t-статистика 0,016932141 P(T<=t) одностороннее 0,493285466 t критическое одностороннее 1,681952358 P(T<=t) двухстороннее 0,986570933 t критическое двухстороннее 2,018081679 распределения рейтинговых данных нормальному закону, хотя и менее четко. Для строгости обоснования выдвигаемой гипотезы далее были отобраны группы в потоках МП-08 и МП-07, соответствующие критерию нормальности, т. е. группы МП-08-01,2 и МП-07-01,2. Отметим, что группы МП-07-01,2 обучались по тем же ГОС, что и последующие учебные группы. Также оставалось неизменным количество аудиторных часов и часов на СРС. При этом не менялся преподаватель, ведущий лекционные практические и лабораторные работы. Таким образом, влияние субъективных возмущающих факторов сведено к минимуму, что дополнительно было проверено статистическими методами.

На рис. 4 представлены ранжированные рейтинговые данные учебных групп МП-07 и МП-08, по которым наблюдается зримое различие в уровне рейтинга разногодовых групп. Визуальное различие далее необходимо подтвердить или опровергнуть статистическими расчетами.

Проведем проверку выдвинутой педагогической гипотезы о неравенстве средних значений рейтинговых баллов по учебным группам консультируемых и не консульти- руемых с помощью ИКТ по средней величине группового рейтингового балла по двухвыборочному t-критерию Стьюдента. Во всех трех случаях проверкой была установлена значимость расхождений в рейтинговых баллах, следовательно, обосновать их отличие случайными возмущениями нельзя.

Единственное обоснование улучшения рейтинговых достижений заключается именно в активном и целенаправленном введении педагогом в учебный процесс нового формата проведения консультаций учащихся в дистанционном формате, так как все остальные условия протекания учебного процесса оказались абсолютно идентичными и однородность групп была проверена выше.

По итогам проведенных исследований можно сделать следующие выводы:

• 1.    Применимость двухвыборочного t-критерия Стьюдента для репрезентативных выборок рейтинговых данных учащихся была предварительно обоснована проверкой нормальности их распределения.

• 2.    Установлено, что как группы, консультируемые с применением ИКТ, так и группы, консультируемые в традиционном формате, однородны внутри собственных множеств по

  

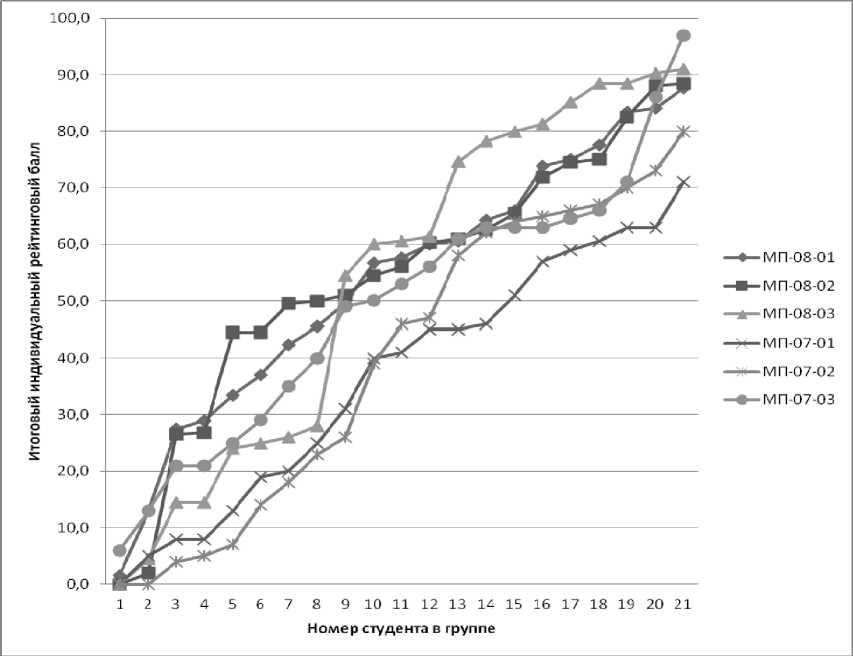
  Рис. 4. Сравнение ранжированных рейтинговых данных МП-07,08

  
  

• 3.    Двухвыборочный t-тест для средних значений групповых рейтинговых баллов как в группах, консультируемых с применением ИКТ, так и в группах, консультируемых в традиционном формате, при уровне значимости α = 0,05 (величина ошибки I рода) установил, что различие в средних значениях группового рейтингового балла (значительное повышение в группах МП-08 по сравнению с группами МП-07) является значимым (не случайным). Наиболее вероятной причиной данного факта при однородности остальных условий протекания учебного процесса, является направленная работа преподавателя по консультированию учащихся в современном инновационном формате – с применением ИКТ, а именно – системы Moodle и коммуникаций социальных сетей, что привело к качественному повышению уровня знаний студентов, выразившееся в их количественном признаке – повышении индивидуальных рейтинговых баллов, и, соответственно, в повышении среднего группового рейтингового балла.

критерию незначимости расхождений среднего группового рейтингового балла.