Проводимость изогнутых углеродных нанотрубок в приближении Дирака

Введение. Задача N -тел. Модель N -тел активно используется для решения широкого круга задач, в которых важную роль играют коллективные процессы. Взаимодействие в задаче N -тел определяется между парами частиц. Cила, действующая на одну i -частицу, является суммой вкладов от всех остальных частиц. Каждое тело системы характеризуется набором параметров (масса, скорость, положение в пространстве). Для определения закона движения всех частиц необходимо уметь рассчитывать ускорения, обусловленные силовым влиянием на нее других частиц:

^N a = Z F j , j = 1 m

где F _j – сила, с которой j -частица действует на -частицу.

Примеры потенциалов взаимодействия приведены в [2; 4]. Для гравитационного взаимодействия, на основании формулы (1), имеем

a

N

= G Z j=1, j«

j- ( r ^{r r} 13 j I r j - Г I

r)

Непосредственные вычисления по формуле (2) являются достаточно ресурсоемкими: для N частиц объем вычислений растет как O( N ²). Поэтому помимо прямых методов

для эффективного моделирования используются и более сложные схемы, позволяющие сократить объем вычислений до O( NlogN ) [5].

Альтернативным способом сокращения времени расчетов является использование технологий параллельных вычислений на графических процессорах. Наиболее продвинутой в настоящее время считается технология CUDA.

Параллельная реализация построена с учетом выравнивания и использованием разделяемой памяти [3]. Механизм взаимодействия нитей друг с другом в CUDA реализован при помощи встроенной функции _syncthreads() [1].

Были проведены тесты параллельной реализации задачи N -тел на графических процессорах GeForсe GTX 850, Tesla C2070. Ускорение оценивалось по отношению к последовательному алгоритму исполняемом на CPU Intel Core i7 (см. рисунок).

Заключение. Параллельные вычисления при моделировании эволюции гравитирующей системы с использованием технологии CUDA показывают свою эффективность и могут варьироваться в зависимости от вычислительной мощности, размерности и специфики задачи, оптимальности написанного кода. Для специализированных графических процессоров в задаче N- тел ускорение вычислений может достигать порядка 100 и более раз.

Вестник ВолГУ. Серия 9. Вып. 13. 2015

ЧЕЛОВЕК И ОКРУЖАЮЩАЯ СРЕДА

Результаты моделирования

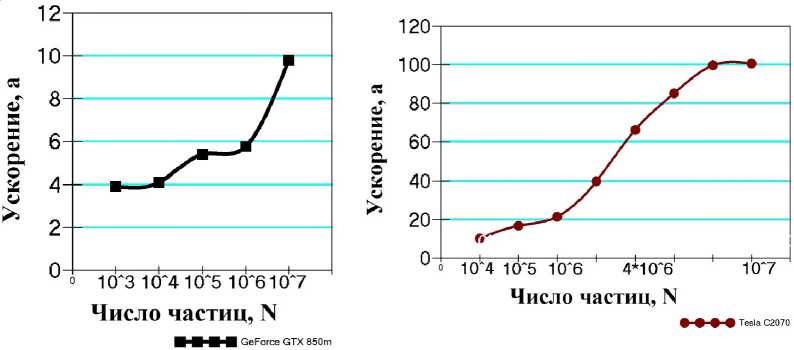
Ускорение в зависимости от размерности задачи