PSO-Based NBI Resistant Asynchronous MC-CDMA Multiuser Detector

Published Online October 2016 in MECS

ing codes (orthogonal code), so a single data symbol is spread in frequency domain to achieve frequency diversity. This feature of MC-CDMA makes it immune to multipath fading. These data symbols are spread and then modulated by different subcarriers using IFFT. So at the output we get different data symbols separated in time domain and at the same time a single data symbol which is sent on different subcarriers gets separated in frequency domain. This feature of MC-CDMA gives multipath fading immunity. Like CDMA, MC-CDMA systems are also affected by the different types of interference such as AWGN (additive white Gaussian noise) and MAI (multiple access interference).MAI is inherent in a CDMA based system because it become very difficult to maintain the orthogonality of spreading waveforms due to several factors such as multipath fading, near-far effect, different timing offsets of different users etc. AWGN on the other hand is inevitable in wireless communication which arises because of random agitation of electrons in electronic devices such as modulators, amplifiers etc. It has been observed that apart from MAI and AWGN, MC-CDMA systems also gets affected by short pulses in frequency domain which is termed as narrowband interference (NBI)[8]. Nowadays due to increased demand for high data rate different techniques such as OFDM, MC-CDMA, UWB (ultra wide band), WLAN (wireless local area network),WIMAX(worldwide interoperability for microwave access), OFDM-LTE (4-G) are being employed. Many times these systems operate simultaneously in co-existence with other systems. In some situations it also happens that these systems have to share the same frequency band with other systems and in such a situation one system may act as narrowband interferer for the other user. It may also happen that some intentional jammer deliberately transmit NBI signals to jam a MC-CDMA system. In CDMA based systems spreading and despreading process of data bits inherently reject the NBI, but high power NBI signal cannot be filtered out because system processing gain cannot be increased beyond a limit due to bandwidth restriction. Existence of NBI degrades the performance of MC-CDMA systems because random NBI signals of variable intensity may overlap with different subcarriers leading to corrupt subcarriers as shown in Fig. 2.

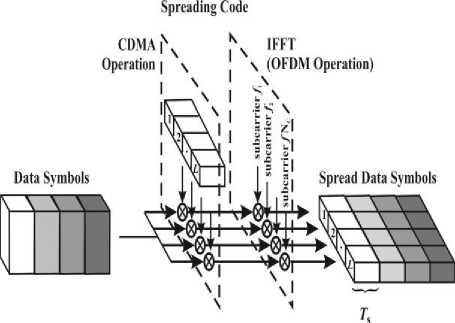
Fig.1. MC-CDMA Transmitter

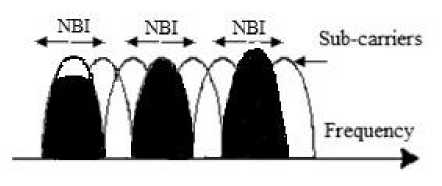
Fig.2. MC-CDMA subcarriers affected by NBI

Verdu in [29] proposes a multiuser detector which detects the different users signals in the presence of MAI. This detector works on the principle of maximum likelihood detection (M-L detection) and detects different users signal by taking 2K (where K is number of users) number of comparisons. Drawback of this detector is that with such a large number of calculations, computational complexity of detector increases with the increase in number of users. To get rid of this problem, various suboptimal detectors have been proposed [30].Suboptimal detectors perform with much lesser number of calculations but their performance slightly degrades. Multiuser detectors based on optimization techniques such as genetic algorithm, evolutionary algorithm etc. have been investigated and it is found that near-optimal solution can be achieved [31-34]. In this paper PSO algorithm has been implemented to optimize the MC-CDMA MUD detector. Earlier Genetic algorithm has been extensively investigated for MUD in MC-CDMA. In comparison with GA, PSO has certain advantages which make this technique more robust and faster. Unlike GA, operations such as mutation and crossover are not performed in PSO. In PSO, best particle is selected after all the particles are engaged in constructive competition [35-38]. In [39-42] some other bioinspired optimization techniques have been applied on different applications.

The rest of the paper is planned as follows. In section II, related work in the literature has been described. MC-CDMA asynchronous receiver model illustrated in section III. PSO has been explained thoroughly in section IV. Section V is for simulation and discussion. Conclu sion has been briefed in section VI.

• II.    R ELATED W ORK

  Various methods and techniques have been proposed for NBI mitigation in CDMA. These methods can be classified into three categories i.e. linear techniques, nonlinear techniques and multiuser detection techniques. In linear techniques, NBI is modelled as a sinusoidal signal with random occurrence. In linear techniques, notch filtering has been a good approach to mitigate NBI. Notch filter is basically a band stop filter Notch filtering can be applied both in frequency domain as well as in time domain. Basic operation of a notch filter is to remove the subcarrier which is affected by NBI signal so it works as a band stop filter [8-12].Estimator /sub tractor method is a time domain method of notch filter to filter out NBI corrupted subcarrier where signal is estimated first and then subtracted from the received signal, filtering out NBI [13-17]. Some adaptive notch filtering method like least mean square (LMS) and weighted least M-estimate were also applied to mitigate NBI [18-19]. In [20] G.J. Saulneir et al . Presents a hybrid technique involving both time domain and frequency domain NBI suppression techniques. In [21] mean square error method is applied by using an N-tap delay filter. In [22] a Gradient Fast Converging (GFC) algorithm was used to mitigate NBI which gives a better performance than LMS based filter. In [23] rake receiver is used to filter out NBI but due to complexity problem they are not preferred. In non-linear methods, NBI is considered as an autoregressive process (random process). In [24] an autoregressive process has been processed by a nonlinear Kalman-Bucy filter. Some other non-linear techniques have been described in [2526].

Methods described above are fit in a situation where NBI is either a sinusoidal signal or an autoregressive process (random process), but in some situations NBI can neither be modelled as sinusoidal nor as autoregressive process. We know that in a spread spectrum communication, transmitted signal gets corrupted by NBI and AWGN on the way to receiver. In such a scenario NBI could be in the form of a digital interferer. So in this type of situation both NBI as well as spread spectrum signal are in digital form. However data rate of NBI is lower than the spread spectrum signal. Moreover all these methods require additional hardware (filters and circuits to perform fourier transforms) to be employed before detector. In such a situation multiuser detection could be applied to mitigate the effect of NBI. Advantage of using multiuser detection is that apart from NBI, MAI and AWGN could also be mitigated simultaneously. Moreover with multiuser detection there is no need to add extra circuitry prior to demodulator (detector) to filter out NBI as it is done in all the methods described above. A prewhitening filter could be employed before the demodulator (detector) if the amount of interference is very large. This filter converts NBI interference to white Gaussian signals [27-28].

• III.    MC-CDMA R ECEIVER

In a MC-CDMA each bit of a single user transmitted on different sub-carriers so it occupies all the bandwidth. Similarly every bit of all the users occupies a large bandwidth and every bit of a single user is spread in frequency domain. Fig. 3 shows an asynchronous MC-CDMA system with K users. Here т is transmission delay associated with K^th user and it can be assumed that 0 <  T 1 <  T 2 < ... <  T k <  T b .

Signals are received on M number of subcarriers and further original transmitted data/symbol is recovered by despreading the orthogonal codes. In this way both OFDM and CDMA operations are performed on receiver side also. In MC-CDMA each symbol is transmitted on different subcarriers thus achieving a good frequency diversity. Here matched filter based correlator circuit has been employed to detect the symbols. Output of matched filter has been given to a PSO based multiuser detector. It detects the bits by minimizing error between transmitted bits and estimated bits.

n (t) = nwg (t) + nnb (t)

Where n(t) is sum of NBI and AWGN. Equation (1) can further be written as:

K

• r m ( t ) = Z ^Ak^hkm ) ( t -^T k ) ^bk ⁺ n ( t )              ⁽²⁾

k = 1

Where, h_m =[ h_{x m},..., h_{K m}^ is spreading code matrix

A = diag [ A,...., A ] is diagonal matrix which represents amplitude of different user signals b = [b,...,bK ]T is transpose bit matrix n = [nx,...,nK]T is transpose of noise matrix which contain both AWGN and NBI

Similarly outputs of different matched filters for m^th subcarrier can be given in matrix form as:

Z_m = R_mAb + n              (3)

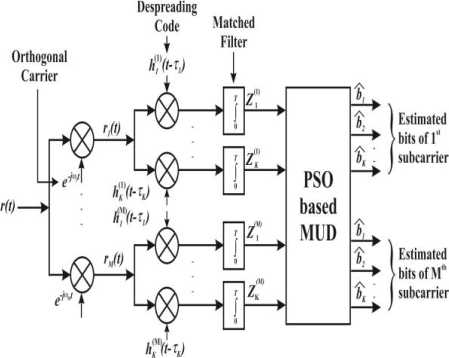
Fig.3. MC-CDMA Receiver Model with PSO

Where R_m is the matrix which contains crosscorrelation values (all non-diagonal values) and autocorrelation values (diagonal values such as P 1.1 , P 2^2, P ³³ , ......, P kk ) of spreading sequences.

R m =

The received signal at the base station on the m^th subcarrier is given as:

r m ⁽ t ) = Z Ah km ^{) (} t — ^T k ) ^b k + n wg ⁽ t > + n nb ⁽ t )        ⁽¹⁾

k = 1

Where,

A_k is the k^th user’s amplitude.

h is the k^th user’s spreading code.

b is the k^th user’s transmitted bit.

n ( t ) is additive white Gaussian noise (AWGN) ,

n(t) is narrowband interference (NBI) modelled as , white Gaussian noise

m

P 11

m ^p 21

m p12

^p 22

.   .    P 1 k

m

.   .    ^p 2 k

L P k 1

m pk 2

^p kk

Fig.4. Cross-correlation matrix

The diagonal auto-correlation values are responsible for the selection of the respective signal at respective matched filter and the non-diagonal cross-correlation values are responsible for the occurrence of MAI. A cross-correlation matrix has been shown in fig.4. In an ideal case values of cross-correlation must be zero if waveforms are perfectly orthogonal, but since in a wireless environment orthogonality of waveforms cannot be maintained. For this very reason multiuser detection has been employed which results in better BER performance and increased system capacity as for as MC-CDMA system is concerned.

The bit vector b which will minimize the error between matched filters outputs Z and the predicted values will be determined by the following equation.

Q m ( b ) = arg j max [2 b^T AZ_m - b^T AR m Ab ] ^ b e { - 1,1} m

Since NBI has been assumed to be white Gaussian noise so it can be added with AWGN.

Hence, for K users MC-CDMA system, a PSO-MUD detector choose a bit vector which will minimize the objective function of equation (4) according to maximum likelihood criterion (M-L detection).

• IV.    P ARTICLE S WARM O PTIMIZATION

PSO has many characteristics which make it different from other optimization techniques such as Genetic algorithm or evolutionary programming. A large number of particles constitute a swarm like structure where each particle moves with its own velocity and this velocity is updated with the constructive interaction with other particles in the swarm. So particles will move to better positions within search space with updated velocity and updated position. Two types of best location are recorded in the process i.e. pbest and gbest. Pbest signifies the best position achieved so far by the particle and gbest is referred to as the best position by any particle in the swarm.

The updating of the particle’s position can be mathematically modelled according the following equation:

V = wV k + c 1 rand 1 (...) x ( pbest - s k ) + c 2 rand 2 (...) x ( gbest - s i )

Where

Vk

Vi  : velocity of particle i at iteration k , w : weighting function, c : social constant (social parameter), normally taken as 2

c : cognitive constant(individual learning rate), normally taken as 2

rand : uniformly distributed random number between 0 and 1 , sk : current position of particle i at iteration k , pbest : pbest of particle i , gbest : gbest of the group.

Where w = wMax - [(wMax - wMin)xiter] / max Iteration    (6)

It is assumed that for best results weight function w is linearly reduced from wMax (normally 0.9) to wMin (normally 0.4).

• A.    Proposed Algorithm Steps

• •    Decide number of users and number of bits per user to run simulation.

• •    Decide the number of users to be corrupted by NBI.

• •    Generate gold codes signature sequences for all the users and calculate cross correlation matrix as per this input.

• •    For a given variance generate white Gaussian Noise.

• •    Generate NBI signals for the users to be corrupted.

• •    Add AWGN as well as NBI to transmitted signal. The received signal at the detector is represented by the equation 3.

• •    Calculate the BER between the received signal and the transmitted bits according to (4).

• •    Set the required parameters for particle swarm optimization (PSO) as given in Table 3 and initialize the PSO.

• •    Evaluate fitness function as in (4).

• •    Update velocity and position of the particles according to the (5).

• •    Update iteration .

• •    Stop when best solution is achieved.

• B.    Flow Chart

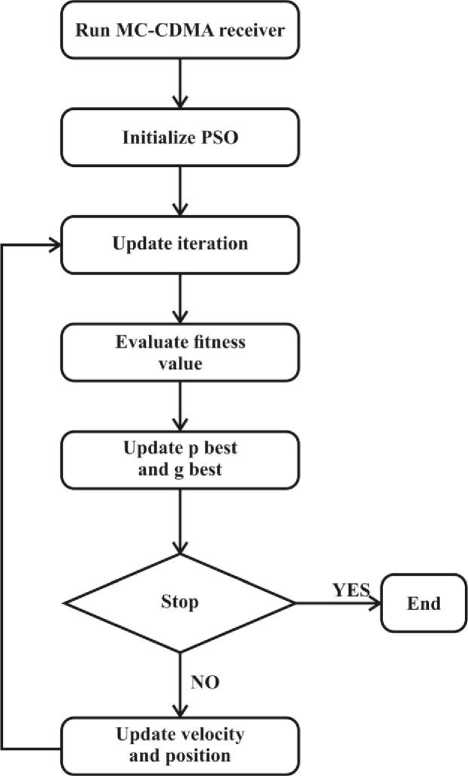
Fig.5. PSO flow chart

• V.    S IMULATION AND R ESULTS

0.9551

0.0164

0.0071

0.0107

0.0263

0.9816

0.0073

0.0191

0.0278

0.0477

1.0058

0.0274

0.0107

0.0068

0.0136

0.9986

To observe the effect of NBI on different user signals, we take 4 users with each user transmitting 10,000 bits through the channel. Here channel is assumed to be synchronous and free from white Gaussian noise. Perfect subcarrier synchronization with no frequency offset is assumed. Objective here is to see the effect of NBI on the received signal.Table.1 shows a matrix where diagonal elements [1 1 1 1] represent the amplitude (autocorrelation) of 4 users signals and non-diagonal elements represents the cross-correlation values. This is an ideal case when channel is free from any type of interference. Now to see the effect of NBI, some of the subcarriers are corrupted by randomly generated NBI of variable intensity. Table 2 shows the amplitude matrix of 4 users corrupted by NBI. It can be clearly observed that amplitudes of users are affected by NBI and also non-diagonal elements become non-zero which indicates that signals are affected by MAI as well because signals no longer remain orthogonal after getting corrupted by NBI.

Table 1. Amplitude matrix of received composite signal without NBI (4 users)

1	0	0	0
0	1	0	0
0	0	1	0
0	0	0	1

Table 2. Amplitude matrix of received composite signal corrupted by NBI (4 users)

10"

s го

ш i5

10"

10"

--♦--OptimumDetector-NBI :

-■♦■- Optimum Detector ■

Г*^^

■           X \

...............

...........'>--k>

.................................ч

-4

10 L--------- L

0         2

4           6          8         10         12

Eb/N(db)

Fig.6. BER for Optimum Detector under the effect of NBI

Table. 2 shows the effect of NBI on multi-carrier sig-nals..Now the proposed algorithm is tested for 16 users and 10000 bits were transmitted for each user. Gold codes of length 31 are used for spreading sequence. Channel is assumed to be asynchronous and corrupted by AWGN. To incorporate the effect of multipath fading, channel is constructed as a Rayleigh frequency selective fading channel where each signal goes through independent fading process. QPSK modulation is used for transmission. Subcarriers are corrupted randomly by NBI of variable intensity. It is assumed that all the users are re- ceived with equal powers i.e. there is no Near-far effect. The simulation is performed for various values of signal to noise ratio to calculate BER every time. Fig.6 shows the BER performance of the optimum detector without any NBI and under the effect of NBI. It can be observed that BER is high under the effect of the NBI. So from this observation it has been proved that NBI affect the performance of MC-CDMA systems i.e. performance of MC-CDMA system degrades in the presence of NBI.

• A.    Convergence of PSO

Convergence properties of PSO have been analyzed extensively in [34-38] for some standard benchmark functions. It can be easily analyzed that PSO is competent and superior in performance as compared to GA. The reason for this performance is due to the fact that in PSO each individual particle interact freely with other particles. In PSO selection, mutation and crossover operations are not performed like GA.

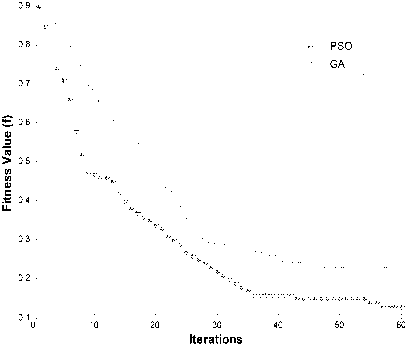
Fig.7. BER for Optimum Detector under the effect of NBI

Table 3. Control parameters of GA and PSO

Genetic Algorithm (GA)		Particle Swarm Optimization (PSO)
Iterations	100	Iterations	100
Selection rate	0.5	Velocity clamping factor	2
Mutation rate	0.15	Cognitive constant	2
Crossover fraction	0.8	Social constant	2
Elitism count	2	Minimum inertia weight	0.4
__	^^^^^—^^^^^—	Maximum inertia weight	0.9

Here simulation is performed for 100 runs using objective function as in equation 8 and control parameters of both algorithms viz. PSO and GA are tuned accordingly. Table 3 shows the tuned parameters of both PSO and GA. It can be observed from the from Fig. 7 that PSO converges to a lower value than GA.

• B.    BER Performance Evaluation

Then the simulation is run for these same values of all the parameters using the proposed algorithm to optimize the BER under the effect of NBI. The parameters mapping with PSO is that number of particles in the PSO was considered as the number of bits/users i.e. 10,000 for this case and number of qualities of the particles are considered as the total number of users i.e. 1 6 in this simulation results. Maximum iterations considered for the PSO was 100. It can be observed from Fig. 8 that the BER using the PSO under the effect of the NBI is reduced and is very close to the BER without any NBI. So it can be clearly analysed that PSO based MUD gives the near optimal detection. Moreover as shown in Fig. 9, PSO takes only around 30 iterations to converge so total number of iterations for all the users in case of QPSK modulation will be around 4×10×30= 1200, whereas in case of optimal detector number of iterations will be 24×10=1099511627776. Hence it can be easily analysed that PSO detector takes 99.99% lesser number of iterations as compared to optimal detector though it gives a near-optimal BER performance.

—*— Optimum Detector - NBI

—♦-- Optimum Detector

PSO - NBI

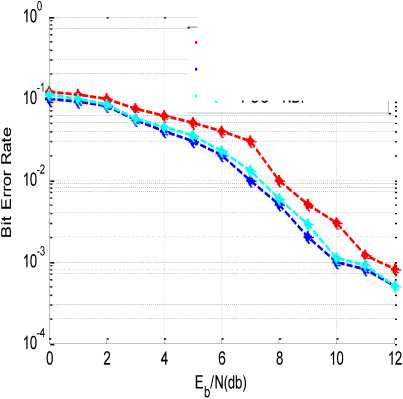
Fig.8. BER Performance

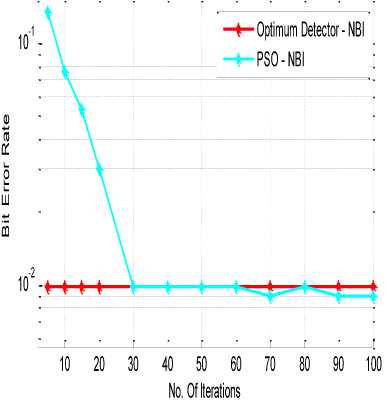
Fig.9. BER vs. No. of iterations

• C.    System Capacity

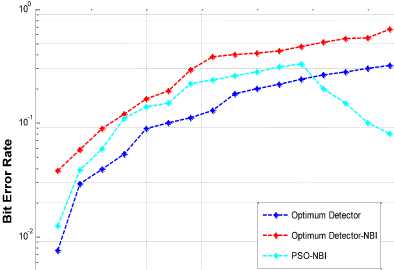
Fig. 10 below shows that with the increasing number of users BER of all the detectors increases. It can be observed from the fig. that BER of PSO based detector shows a downward trend when users are around 25. The reason for this performance is due to the fact that number of users has no role in the convergence of PSO. So it can be concluded that with PSO based detector system capacity increases.

10           15          20          25          30          35

No. of Users

Fig.10. BER for Optimum Detector under the effect of NBI

• VI.    C ONCLUSION

In this paper we proposed a new technique for suppressing the narrow band interference (NBI) by combining the optimum detector with Particle Swarm Optimization technique. It has been demonstrated that NBI can be mitigated without using filters and other circuitry. Our simulation results show that the proposed algorithm minimizes the BER under the effect of NBI and gives performance very near to the optimum detector without any NBI. Moreover computational complexity of PSO detector shows a reduction by 99.99% as compared to optimal detector. Different versions of PSO can be further explored to apply on MUD as a future work.