Расчет 3D-формы гиперупругого тела для моделей нелинейной теории упругости методом Ньютона

DOI:

В природе существует множество материалов, которые подвергаются различным деформациям. Материалы имеют разное поведение под механической нагрузкой. Так, одни (например, металлы: железо, олово, медь и другие) показывают линейно-упругое поведение до перехода в состояние плавления, после чего подвергаются неустранимой пластичной деформации перед разрушением. Хрупкие материалы — стекло, керамика показывают незначительное линейно-упругое поведение, и без пластичной деформации перед разрушением. Материалы, которые сохраняют свои упругие свойства и допускают большие нелинейные деформации, называются гиперупругими. Примером могут служить резина, разные виды полимеров, эластомеров, пена, биологические материалы и др. Они широко используются в различных отраслях, как новые технологичные материалы в строительной отрасли, или при изготовлении различных резиновых и резинометаллических деталей в машиностроении.

Перед применением материалов важно произвести численные расчеты на надежность эксплуатации, исследовать поведение при деформациях. При этом далеко не для всех материалов в литературе были опубликованы полные численные исследования.

В рамках данной статьи приводится краткий обзор основных формул нелинейной теории упругости, и дается полное описание алгоритма численного расчета деформаций гиперупругих материалов методом Ньютона. Следует также отметить, что нелинейная теория упругости освещается в работах [7; 8; 11; 12], в которых подробно описываются основные положения и теоремы, использованные в данной статье, и приводится обширная библиография. Также по данному вопросу можно отметить статьи: [1; 4; 9; 10; 13].

В ходе научной работы на основе проведенных исследований был разработан программный комплекс, реализующий нижеописанный алгоритм минимизации методом Ньютона, а также другие алгоритмы минимизации, в частности методом градиентного и координатного спуска, подробное описание которых приводится в статье [4].

1.    Гиперупругость

Рассмотрим некоторое сплошное тело B , которое занимает определенную область Q 0 в своем исходном, недеформированном состоянии в момент времени t = 0 (рис. 1). При этом, когда происходит смещение точек тела, например Р в Р ‘ (представленных в общем случае на рисунке 1 векторами X и х в декартовой системе координат), и Q в Q' из области Q 0 в область Q _t соответственно при некотором t >  0 , то такая новая конфигурация тела Q _t называется деформированной, а само изменение взаимного расположения точек тела называется деформацией.

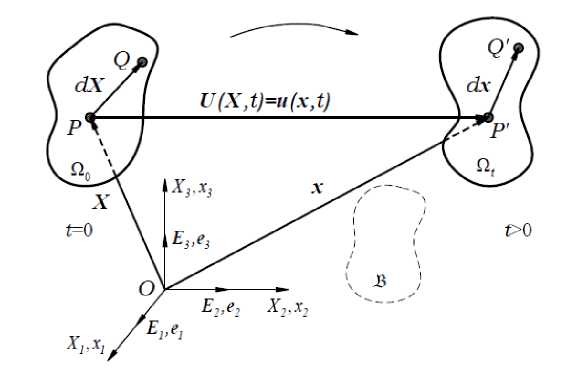
Рис. 1. Деформация тела B

При этом мерой изменения формы в каждой точке тела при деформации является тензор второго ранга F [11]:

F (X,t) =grad X (x,t) = ^dx(X ,^,                      (1)

dX который называется градиентом деформации.

Одним из ключевых свойств объектов с гиперупругим материалом является существование для них функции запасенной энергии [8, с. 168]. Пусть в некоторой области Q , лежащей в R ” , М _п — множество матриц F порядка п и Ж (x,F ) : Q х М _п ^ R + — некоторая непрерывная положительная функция. Для отображения ф : Q ч R ” определим функционал Ф(ф) запасенной энергии по формуле [8; 10; 13]:

Ф(ф) = У Ж(x,Dф(x))dx.

Также предполагаем выполнение условия Липшица

| Ж(x ‘ ,F ) - Ж «F ) |< L | x ‘ — x ‘‘ \                       (3)

с постоянной L >  0 , независящей от F Е М _п . При этом в нелинейной теории упругости рассматривается функция Ж (x,F ) вида

Ж(x, F ) = Ж(x, | F | , Adj(F), detF),                          (4)

где | F | ² = tr(FF ^т ) ( tr или след матрицы — сумма элементов главной диагонали); det F — определитель матрицы F , характеризующий соотношение изменения объема при деформации [11, p. 18]. И, в случае det F > 0 (тогда существует обратная матрица F ), Adj(F) = F ^-т detF . Также заметим, что зависимость от x могут дополнительно характеризовать внешние поля сил, например, сила тяжести.

Решение задачи поиска формы деформированного тела достигается за счет минимизации вышеуказанного функционала [10; 13]. В случае итерационного процесса минимизации функционала требуется выполнение условий на границе и условий принадлежности классу допустимых деформаций, который мы можем задать функцией М (x) Е L ^s (Q) , s > п — 1 , для которой справедливо условие [1; 15]

< М (x).                                  (5)

det(^ф)

Также заметим, что для глубокого анализа, помимо моделирования ограничений, требуется представление различных численных характеристик деформированного объекта. В качестве одного из важных элементов, характеризующих деформацию, часто выступает тензор напряжения Коши σ . Одним из способов вычисления которого выступает формула, связывающая тензор напряжения Коши (напряжение в деформированном теле) и первый тензор Пиолы — Кирхгофа Р (напряжение относительно исходного состояния) [11, p. 22]:

дЖ dF’ о =(detF)-1PFт.                             (6)

2.    Пространственная дискретизация Применим метод конечных элементов, который аналогичен для задач линейных упругих деформаций [2]. Проведем разбиение данного сплошного тела Q на п-мерные симплексы (выпуклая оболочка точек) Si, S2,..., Sm с вершинами р1 ,р2,... ,рп. Разбиение произведем методом Делоне [3; 6], в частности, разбиение производится на тетраэдры.

Заметим, что градиент деформации можно приближенно рассматривать как линейную зависимость между исходной и текущей формой. Для произвольной точки и ее бесконечно малых соседей градиент деформации можно точно аппроксимировать, используя линейное соотношение [5; 15, p. 15]

х = ф ( Х ) ^FX + b.

Тогда для каждой вершины рассмотрим аффинное отображение ф(х) = F _k (х) + + b _k ,х Е S _k ,F _k Е M _n ,b _k Е R ⁿ , на каждом симплексе S _k ,к = 1, 2,...,т , в который входит рассматриваемая точка. Пусть q ₀ , q 1 ,... ,q _n — вершины симплекса S _k , V j = Ф(^ j ) , для j = 0, 1,... ,п , и I — индекс рассматриваемой вершины. Тогда определим матрицу Q _k , поместив в ее столбцы q j — q i ,j = I , и аналогично матрицу V _k , разместив в столбцах V j — v _l ,j = / . Получаем

F k = V k *Q - 1 . (8)

Заметим, что произведение V _k Q ^— не зависит от порядка нумерации вершин симплекса S _k , и соответственно однозначно определяется только множеством его вершин и значений отображений.

При этом функция запасенной энергии и ее численная аппроксимация определяются следующей формулой [4, c. 57–58]:

m                m

Ф( ф ) = Jq^W (х, ^ПФ (х))^х = ^ J_s Ж(х,В ф (хУ) ^ ^ Ж (x _{S k} ,F k )IS k | ,     (9)

где | S _k | — n -мерная мера Лебега (объем тетраэдра); x s _k — геометрический центр; функция Ж (x s _k ,F _k ) — формула напрямую зависящая от модели выбранного гиперупругого материала, например, Муни — Ривлина, Огдена, Адамара — Грина и др.

В случае моделирования ограничений М(х) (формула 5) имеем следующую аппроксимацию ( L i — число симплексов, инцидентных вершине p _i ):

|D ф (P i )\ ^п ^ £ _v   | F k | ^п

det(^(p i ))    L i ^ det(F k ) ^.

P i ^^s k

Тогда, имея формулу численной аппроксимации запасенной энергии, задача сводится к минимизации данного функционала Ф( ф ) .

3.    Решение методом Ньютона

Рассмотрим теперь решение задачи минимизации функционала Ф( ф ) дэмпирован-ным методом Ньютона второго порядка.

Процесс расчета начинается с выбора нулевого приближения, затем последовательно выбираются вершины р 1 ,... ,р ^ , для которых и вычисляется минимум величин:

52 Ж (x, S k ,F k ) | S k | , 52 Ж (x, S k ,F k ) | S k | ,..., 52 Ж (x s k ,F k )S | .        (11)

P l ^ S k                      P 2 ^ S k                            P n E S k

В общем случае метод Ньютона второго порядка определяется как приближение f (x + dx) ~ f (x) + < V f (x), dx > +- < V2 f (x)dx, dx > .          (12)

Приравняв к нулю градиент квадратичной аппроксимации и решив получившееся линейное уравнение, мы получаем следующий итеративный алгоритм спуска:

x t+i = x t - a _t V 2 f ^-1 (x _t )Vf (x t ),                           (13)

где V 2 f(x _t ) — матрица Гессе; a _t E (0,1] — размер шага; Vf(x _t ) — матрица Якоби функции f (x _t ) — величины из формулы (11).

Рассмотрим процесс формирования матриц Q и V . Важным моментом является определение порядка, какую из какой вершины мы вычитаем при формировании столбцов матриц — будет ли он фиксирован, или зависеть от индекса рассматриваемой вершины в текущем симплексе. С одной стороны, порядок и не так важен (но он обязательно должен быть одинаков между соответствующими матрицами Q и V ), так как значение матрицы F , и в целом расчеты матриц Гессе и Якоби, не зависят от порядка. Соответственно мы можем сделать как более универсально, разместив вектора так, что, например, в последнем столбце всегда будет вектор p i — p i - 1 , а в остальных p j — р - 1 , j = I и j = I — 1 . Однако мы можем заметить следующий факт, что матрица Q , при условии одинакового порядка вершин, на протяжении итераций не меняется, как и сопутствующие величины, например обратная матрица к Q , или объем симплекса. Соответственно, в целях более высокой производительности, нет смысла пересчитывать их на каждой итерации. Стоит произвести расчеты один раз на первой итерации и запомнить. Но в этом случае матрицы Q и V мы должны для всех вершин формировать в строго определенном порядке.

Приведем псевдокод алгоритма минимизации методом Ньютона, с учетом формирования столбцов матриц Q и V , как p j — р ₀ , j = 1,... ,п , и с использованием центральной разностной производной при расчете матрицы Гессе и вектора Якоби.

void Минимизации(){ расчетНеизменяемыхХарактеристик(); расчетИзменяемыхХарактеристик(); bool breakFlag = false;

while(!breakFlag)

выполнитьИтерациюМинимизации(трансфОбъект); расчетИзменяемыхХарактеристик();

if (текущееЗначениеФ < предыдущееЗначениеФ) предыдущееЗначениеФ = текущееЗначениеФ;

else трансфОбъект = трансфОбъектНаПредыдущемШаге; breakFlag = true;

}

В методе расчетНеизменяемыхХарактеристик() производится расчет матриц Q , обратной матрицы QI = Q ^-1 , объема S | и геометрического центра x g _k .

В методе расчетИзменяемыхХарактеристик() на каждой итерации идет расчет новых матриц V и F , текущееЗначениеФ , равное значению запасенной энергии Ф (трансфОбъект) , которое рассчитывается по формуле (9).

Дальше рассмотрим псевдокод одного итерационного шага метода выполнитьИ-терациюМинимизации(трансфОбъект) и соответствующие вычисления матриц Якоби и Гессе (в методах W(matrix F) идет расчет численного значения согласно формуле выбранной модели материала):

void выполнитьИтерациюМинимизации(трансфОбъект){ for(для всех вершин pi) трансфОбъект[pindex] = трансфОбъект [pindex] – epsilon *

Гессе(pindex, шаг).обратнаяМатрица() * Якоби(pindex, шаг); } vector3D Якоби(pindex, шаг){ vector3D якоби; vector VR, VL; for (int i = 0; i < 3; i++) double правоеСмещение = 0, левоеСмещение = 0; for (для всех симплексов Sk, в которые входит вершина pi) int sk = индексСимплекса, l = номер вершины pi в симплексе; VR[k] = VL[k] = V[sk]; if (l == 0) { VR[k][i] -= шаг; VL[k][i] += шаг; } else { VR[k][i][l-1] += шаг; VL[k][i][l-1] -= шаг; } правоеСмещение += W(VR[k] * QI[sk]) * Объем[sk]; левоеСмещение += W(VL[k] * QI[sk]) * Объем[sk]; якоби[i] = (правоеСмещение – левоеСмещение) / (2 * шаг); return якоби; } matrix3D Гессе(pindex, шаг){ matrix3D гессе; vector3D fPlus, fMinus; vector vTemp; for (int i = 0; i < 3; i++) for (для всех симплексов Sk, в которые входит вершина pi) int sk = индексСимплекса, l = номер вершины pi в симплексе; vTemp[k] = V[sk]; if (l == 0) vTemp[k][i] -= шаг; else vTemp[k][i][l-1] += step; fPlus[i] += W(vTemp[k] * QI[sk]) * Объем[sk]; if (l == 0) vTemp[k][i] = V[sk][i] + шаг; else vTemp[k][i][l-1] = V[sk][i] – шаг; fMinus[i] += W(vTemp[k] * QI[sk]) * Объем[sk]; гессе[i][i] = (fPlus[i] - 2 * текущееЗначениеФ + fMinus[i]) / (4 * step * step); for (int i = 0; i < 3; i++) for (int j = i + 1; j < 3; j++) double f = 0.; for (для всех симплексов Sk в которые входит вершина pi) int sk = индексСимплекса, l = номер вершины pi в симплексе; vTemp[k] = V[sk]; if (l == 0) { vTemp[k][i] -= step; vTemp[k][j] -= step; } else { vTemp[k][i][l-1] += step; vTemp[k][j][l-1] += step; } f += W(vTemp [k] * QI[sk]) * Объем[sk]; гессе[i][j] = (f - fPlus[i] - fPlus[j] + текущееЗначениеФ) /

(4 * step * step);

return гессе.Транспонированная();

}

При реализации данного алгоритма средствами языка С++ отметим, что хороший прирост к производительности показало использование библиотеки линейной алгебры Eigen, в частности для ускорения расчетов обратных матриц. Также, поскольку расчеты движений вершин в одном итерационном шаге не зависят между собой, то распараллеливание данного цикла приводит к кратному ускорению расчетов.

4.    Программная реализация

В ходе научной статьи был разработан программный комплекс «Программа для расчета 3D формы упругого тела для моделей нелинейной теории упругости на основе триангуляции Делоне» на языке С++ и фреймворка Qt. Данная программа предназначена для проведения расчетов деформаций с учетом моделирования ограничений гиперупругих материалов, таких как материалы Муни — Ривлина, Огдена, Адамара — Грина, Сен-Венана — Кирхгофа, неогуковы материалы. Присутствует возможность как выбора для расчетов перечисленных материалов, с учетом введения собственных коэффициентов и возможности задания выпуклых функций в качестве дополнительных слагаемых, например, для материала Адамара — Грина, так и задание полностью своей собственной формулы материала.

Программа дает возможность визуализации с трехмерным обзором, в том числе визуализации на каждой итерации применяемых изменений при расчете деформации.

Программа позволяет как импортировать объекты для дальнейшей обработки в формате obj, так и экспортировать в obj рассчитанные результаты.

На данную программу было получено свидетельство о государственной регистрации программы для ЭВМ № 2023668031.

Представим демонстрацию одних из расчетов разработанной программы. Для примера возьмем пластину размером 2 х 1 х 0,1 и произведем тетраэдризацию методом Делоне, разбив ее на 29 тыс. тетраэдров (см. рис. 2). В программе тетраэдризация производится за счет использования внешней библиотеки tetgen.

Дальше подвергнем объект с целью деформации приложению некоторых сил. В программе данная возможность пока присутствует за счет применения к объекту некоторых, введенных пользователем формул аффинных преобразований. Например, выполним для каждой координаты х данной пластины аффинное преобразование х + 0, 5cos(6y) — это послужит нам приближением деформации пластины на нулевом шаге (см. рис. 3).

Зададим шаг = 0,001, epsilon = 0,005, и выберем для объекта материал Муни — Ривлина W(x,F ) = a\F | ² +b | AdjF | ² +r(detF) , установив r(detF) = 2(detF - 1) 2 — 2(a+ + 2b)ln(detF ) — 3(a + b) , со значениями параметров a = 25 , b = 0,1 , с = 2 . Применим к данному объекту с вышеперечисленными условиями минимизацию методом Ньютона в количестве 2 500 итераций. В результате получим уменьшение запасенной энергии Ф с 17,29 (на итерации 0) до 6,73 (на итерации 2 500), допустимую деформацию М , равную 34,9 на последней итерации, и визуальную демонстрацию на рисунке 4, где красным отображается результирующий объект, а синей сеткой — бывшая фигура на нулевом приближении.

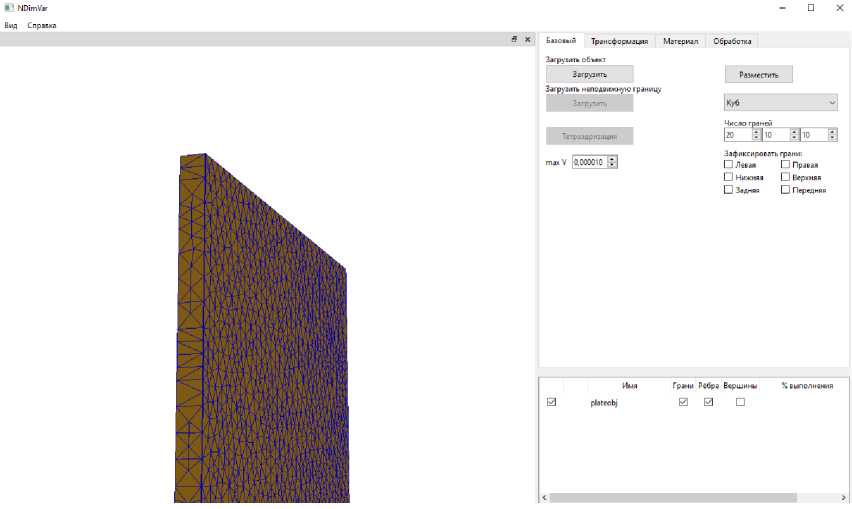
Рис. 2. Вид главного окна с возможностью 3D-обзора исходного объекта с произведенной тетраэдризацией

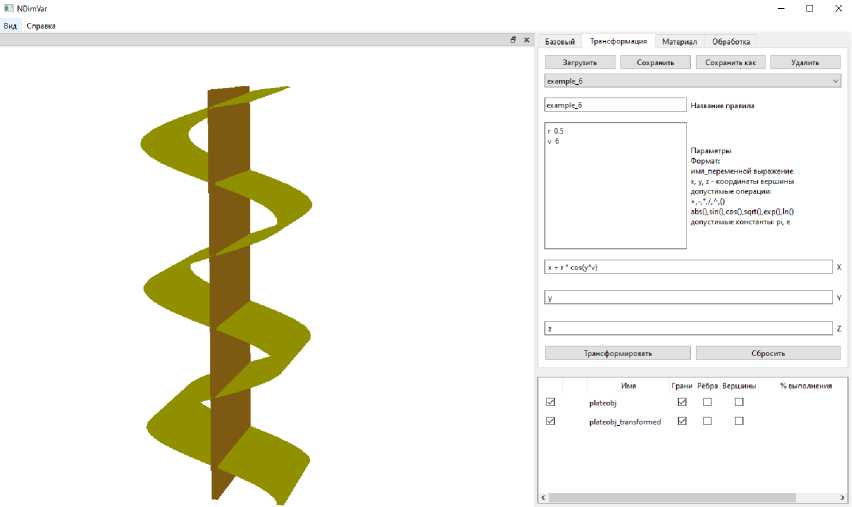
Рис. 3. Применение к объекту с рисунка 2 внешних сил, определенных формулами вкладки Трансформация — отображение желтого объекта как нулевого приближения

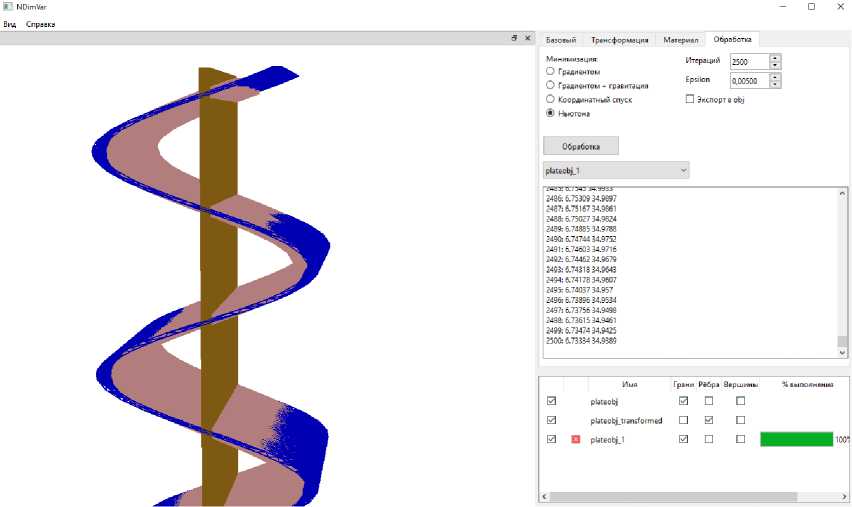
Рис. 4. Применение к объекту с рисунка 3 минимизации методом Ньютона, при выбранном материале Муни — Ривлина — результат светло-красный объект, темно-синей сеткой отображается объект на нулевом приближении

Заключение

В данной статье был описан способ расчета деформаций для объектов с гиперупругими материалами. Приведен алгоритм минимизации методом Ньютона, позволяющий решить данную задачу с учетом допустимых деформаций. Также было разработано программное обеспечение, реализующее данный алгоритм и визуализирующее рассчитанные результаты для различных моделей гиперупругих материалов.