Расчет аварийных режимов фидера 35 кВ с двухцепной линией

Солдатов В.А.; Яблоков А.С.; Soldatov V.A.; Yablokov A.S.

Научные статьи \ Прикладные науки. Медицина. Технология \ Инженерное дело. Техника в целом \ Общее машиностроение. Ядерная технология. Электротехника. Технология машиностроения \ Электротехника

Расчет аварийных режимов фидера 35 кВ с двухцепной линией

Автор: Солдатов В.А., Яблоков А.С.

Журнал: Вестник Красноярского государственного аграрного университета @vestnik-kgau

Рубрика: Технические науки

Статья в выпуске: 11, 2016 года.

Бесплатный доступ

В распределительных сетях 35 кВ актуаль-ной является задача расчета аварийного режима, а также задача определения вида и места аварийного режима. При расчете ава-рийных режимов в основном применяют два метода: метод трех симметричных состав-ляющих и метод фазных координат. В сетях класса 110 кВ и выше при расчете аварийно-го режима уже широко используется метод фазных координат. В распределительных электрических сетях 6-10-35 кВ этот ме-тод применяется пока ограничено. Данная работа является продолжением исследова-ний, ведущихся на кафедре информационных технологий в электроэнергетике ФГБОУ ВО «Костромская ГСХА». В предыдущих работах представлены как методы расчета аварий-ных режимов, так и методы определения их вида и места в распределительных электри-ческих сетях. Так, например, показано, что определение вида и места аварийного режи-ма возможно осуществить по величинам наведенных напряжений на специальных ан-теннах, расположенных под фазами линии электропередачи. Данные исследования вы-полнены для одноцепных линий сетей 10 и 35 кВ. Однако часто фидер 35 кВ содержит двухцепную линию. Для проведения исследо-ваний сначала необходимо иметь методику расчета аварийных режимов фидера 35 кВ с двухцепной линией в фазных координатах, которая представлена в данной статье. По-лучены матричные выражения для напряже-ний и токов во всех точках фидера в зависи-мости от параметров участка фидера и из-вестных напряжений в начале. Расчетная схема фидера содержит: питающий транс-форматор с соединением обмоток «звезда - треугольник»; первый участок двухцепной линии; второй участок двухцепной линии; блок несимметрии, моделирующий аварий-ные режимы; третий участок двухцепной линии; первый потребительский трансфор-матор; второй потребительский транс-форматор; нагрузку в конце первой цепи; нагрузку в конце второй цепи. Разработан-ную методику можно использовать как при расчете самих аварийных режимов, так и при решении задачи определения вида и места аварийных режимов в распределительных электрических сетях.

Еще

Аварийный режим, фи-дер 35 кв, двухцепная линия, расчетная схе-ма, фазные координаты, место и вид режи-ма, наведенное напряжение

Короткий адрес: https://sciup.org/14084546

IDR: 14084546 | УДК: 621.314

Double-circuit line of 35 kV feeder emergency operation calculation

In distributive networks of 35 kV the problem of calculation of emergency operation, and also the problem of definition of the kind and place of emergency operation is actual. At calculation of emergency operations two methods are generally applied: the method of three symmetric compo-nents and the method of phase coordinates. In the networks of the class of 110 kV and above at calculation of emergency operation the method of phase coordinates is already widely used. In dis-tributive electric networks of 6-10-35 kV this method is seldom applied. This work is the con-tinuation of the researches which were conducted on the chair of information technologies in FSBEE HE “Kostroma agricultural academy”. In the previ-ous works both methods of calculation of emer-gency operation were presented, and the meth-ods of definition of their kind and place in distribu-tive electric networks. So, for example, it is shown that it is possible to carry out the definition of the kind and place of emergency operation in sizes of the induced tension on the special antennas lo-cated under power line phases. These researches were executed for one-chain lines of networks 10 and 35 of kV. However, the feeder of 35 kV often contains a two-chain line. For carrying out re-searches at first it is necessary to have the meth-od of calculation of emergency operation of the feeder of 35 kV with a two-chain line in phase coordinates which is presented in this study. Ma-trix expressions for tension and currents in all points of the feeder depending on parameters of the site of a feeder and known tension at the be-ginning were received. The settlement scheme of the feeder contained the feeding transformer with connection of windings "a star - a triangle"; the first site of a two-chain line; the second site of a two-chain line; the asymmetry block modeling emergency operation; the third site of a two-chain line; the first consumer transformer; the second consumer transformer; loading at the end of the first chain; loading at the end of the second chain. The developed technique can be used both in calculation of emergency operation, and in the solution of the problem of definition of the kind and place of emergency operation in distributive electric networks.

Еще

Текст научной статьи Расчет аварийных режимов фидера 35 кВ с двухцепной линией

Введение. В распределительных электрических сетях 6 – 10 – 35 кВ с изолированной нейтралью актуальной является задача расчета аварийных режимов (АР), а также задача определения их вида и места [1]. Аварийный режим можно рассчитать или методом трех симметричных составляющих, или методом фазных координат (ФК). Метод ФК является матричным методом расчета. В электрических сетях класса 110 кВ и выше метод ФК хорошо себя зарекомендовал. В распределительных электрических сетях этот метод применяется пока ограничено. Метод ФК позволяет рассчитывать фазные напряжения и токи в реальных величинах. Целью представленных исследований является разработка методики расчета аварийных режимов фидера 35 кВ, содержащего двухцепную линию. Без расчета АР невозможно создавать методики и приборы их обнаружения, а также разрабатывать различные критерии определения вида и места АР [2]. Также одним из методов определения вида и места АР является метод рассмотренный в [3, 4]. Аварийные режимы определяются по наведенным напряжениям на специальных антеннах, расположенных под фазами линии параллельно им. Чтобы рассчитать наведенные напряжения на антенне, необходимо знать напряжения на фазах линии в начале и конце участка линии, параллельно которому размещена антенна. Таким образом, сначала необходимо рассчитать сами аварийные ре- жимы, а затем наведенные напряжения. Для одноцепной линии эта задача рассмотрена в [3, 4]. Представляет интерес разработка методики расчета аварийных режимов в случае, когда фидер содержит двухцепную линию.

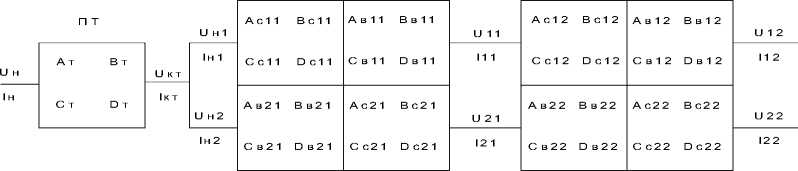
Расчетная новая схема с двухцепной линией представлена на рисунке. Она отличается от расчетной схемы при одноцепной линии тем, что многополюсники A, B, C, D имеют размерность матриц 6 на 6, а не 3 на 3, а также содержит два потребительских трансформатора и две нагрузки. Это позволяет учесть электромагнитные влияния между всеми шестью фазами двухцепной линии, что ранее не было представлено в теории расчета аварийных режимов распределительных электрических сетей.

ЛЭП-1

ЛЭ П-2

БН

ЛЭП-3

ТП

Н агрузка 1

U12

Aс13

Bс13

Aв13

Bв13

U13

Aс14

Bс14

Aв14

Bв14

U14

Aт1

Bт1

Uт1

Aн1 Bн1

Uк1

I14

Iк1

I12

Cс13

Dс13

Cв13

Dв13

I13

Cс14

Dс14

Cв14

Dв14

Cт1

Dт1

Iт1

Cн1 Dн1

ТП

Нагрузка 2

U22

Aв23

Bв23

Aс23

Bс23

U23

Aв24

Bв24

Aс24

Bс24

U24

Aт2

Bт2

Uт2

Aн2 Bн2

I22

Cв23

Dв23

Cс23

Dс23

I23

Cв24

Dв24

Cс24

Dс24

Uк2

I24

Cт2

Dт2

Iт2

Cн2 Dн2

Iк2

Расчетная схема фидера, содержащего двухцепную линию (нижняя часть рисунка является продолжением верхней части)

На рисунке обозначено:

ПТ – питающий трансформатор с соединением обмоток «звезда – треугольник»;

ЛЭП-1 – первый участок двухцепной линии, параллельно которому будет размещена антенна;

ЛЭП-2 – второй участок двухцепной линии;

БН – блок несимметрии, моделирующий аварийные режимы;

ЛЭП-3 – третий участок двухцепной линии;

ТП 1 – первый потребительский трансформатор;

ТП 2 – второй потребительский трансформатор;

Нагрузка 1 – нагрузка в конце первой цепи;

Нагрузка 2 – нагрузка в конце второй цепи.

Получим методику расчета АР двухцепной линии, используя метод ФК как это сделано в [3] для одноцепной линии. Каждый из перечисленных элементов можно представить своей матрицей передачи H , содержащей блоки А, B,

C, D с соответствующими индексами. Тогда напряжения и токи в начале элемента Uн, Iн можно выразить через напряжения и токи в конце элемента Uк, Iк по формуле

Uh Uk t = H ■ i

Iн Iк

A B 1 [ Uk

C D ' Ik

Запишем выражения для напряжения и токов, используя матрицы передачи всех элементов согласно рисунку.

Напряжения и токи в начале фидера:

Uh _ Am Вт Ukt

Ih = Cm Dm ' 1кт

Напряжения и токи в начале первого участка линии:

^_ Uh1		" Ас11	Bс 11	Aв 11	Be11~		’ U 11"
Ih1		Cс 11	Dс 11	Cв 11	De11		I 11
Uh 2	— =	Ав 21	Bв 21	Aс 21	Be 21	•	U 21	. (2)
_ Ih 2 _		_ Ce 21	Dв 21	Сc 21	De 21 _		_ 1 21 _

Напряжения и токи в начале второго участка линии:

Г U 111		^_ Ас 12	Bс 12	Aв 12	Be12^_		' U 12^_
1 11		Cс 12	Dс 12	Cв 12	Dв 12		I 12	.
U 21	— =	Ав 22	Bв 22	Aс 22	Bс 22	•	U 22	(3)
1 21		Ce 22	Dв 22	Сc 22	De 22		1 22

Учтем граничные условия:

– токи после нагрузки равны нулю:

1к1 = 0, Ik 2 = 0,(10)

– напряжения в начале:

Uh1 = Uh 2 = Ukt ,(11)

– ток в начале:

1кт = Ih1 + Ih 2.(12)

После преобразования (1)–(12) получим следующие выражения для напряжений и токов во всех точках двухцепного фидера:

Напряжения и токи в начале блока несим-метрии:

' Uh 1 = ( Аэн1 • AET 1 + Аэвн 1 • AET 2) • Uh

Ih 1 = ( Сэн1 • AET 1 + Сэвн 1 • AET 2) • Uh

^_ U 12 1 Г Ас 13 Be 12 Ав 13 Be 13 1 Г U 13 1

1 ¹² = Ce 1³ De 1³ Ce 1³ De 1³ , I 13 .

U 22 Ав 23 Be 23 Ас 23 Be 23 U 23 ⁽⁴⁾

Uh 2 = ( Аэвн 2 • AET 1 + Аэн 2 • AET 2) • Uh ^v '

Ih 2 = ( Cэeн2 • AET 1 + Cэн 2 • AET 2) • Uh

122 Ce 23 De 23 Cc 23 De 23 1 23

Напряжения и токи в начале третьего участка линии:

' U 11 = ( Аэ11 • AET 1 + Аэв 11 • AET 2) • Uh

1“ . _ “1 1“ .. . . ..“11“ ..“1

U 13 Ас 14 Bc 14 Ав 14 Be 14 U 14

1 13 Ce 14 Dc 14 Ce 14 De 14 1 14 . ._.

U 23 = Ав 24 Be 24 Ас 24 Be 24 ’ U 24 ⁽⁵⁾

1 11 = ( Сэ11 • AET 1 + Сэё11 • AET 2) • Uh , U 21 = ( Аэв 21 • AET 1 + Аэ 21 • AET 2) • Uh ⁽¹⁴⁾

1 21 = ( Cэe 21 • AET 1 + Cэ 21 • AET 2) • Uh

1 23 Ce 24 De 24 Cc 24 De 24 1 24

Напряжения и токи в начале первого потребительского трансформатора:

U 12 = ( Аэ 12 • AET 1 + Аэв 12 • AET 2) • Uh

U 141 Г Ami Bm1 1 [ Um1

1 14 = Cmi Dmi ’ Imi

1 12 = ( Сэ 12 • AET 1 + Сэв12 • AET 2) • Uh , U22 = ( Аэв22 • AET 1 + Аэ 22 • AET 2) • Uh

122 = ( Сэе22 • AET 1 + Сэ 22 • AET 2) • Uh

Напряжения и токи в начале второго потребительского трансформатора:

U 24 1 _ Г Am 2 Bm 2 1 Um 2'

1 24 = Cm 2 Dm 2 ’ Im 2

Напряжения и токи в начале первой нагрузки:

Um1 Ah1 Bh1 Uk 1

Im1 = Ch 1 Dh1 ’ Ik1

’ U 13 = ( Аэ 13 • AET 1 + Аэе 13 • AET 2) • Uh 1 13 = ( Сэ 13 • AET 1 + Сэе 13 • AET 2) • Uh , U 23 = ( Аэв 23 • AET 1 + Аэ 23 • AET 2) • Uh , 1 23 = ( Cэe 23 • AET 1 + Cэ 23 • AET 2) • Uh

Напряжения и токи в начале второй нагрузки:

Um 2 1 _ Г Ан 2 Bh 2 1 [ Uk 2

Im 2 = Ch 2 Dh 2 ’ Ik 2

U 14 = Аэ 14 • AET 1 • Uh

1 14 = Сэ 14 • AET 1 • Uh U 24 = Аэ 24 • AET 2 • Uh ’

1 24 = Cэ 24 • AET 2 • Uh

Umi = Ан1 • AET 1 • Uh

Аэ11 = Ас 12 • Аэ 12 + Вс 12 • Сэ 12 + Ав 12 • Аээ 22 + Вв 12 • Сээ 22,

Im1 = Сн1 • AET1 • Uh

Um 2 = Ah 2 • AET 2 • Uh

Im 2 = Ch 2 • AET 2 • Uh

Аээ11 = Ас 12 • Аээ 12 + Вс12 • Сээ 12 + Ав 12 • Аэ 22 + Вв 12 • Сэ 22,

Сэ11 = Сс 12 • Аэ 12 + Dс 12 • Сэ 12 + Св 12 • Аээ 22 + Db 12 • Сээ 22,

Сээ 11 = Сс 12 • Аээ 12 + Dс 12 • Сээ 12 + Св 12 • Аэ 22 + Db 12 • Сэ 22,

Аэ 21 = Ав 22 • Аээ 12 + Вв 22 • Сээ 12 + Ас 22 • Аэ 22 + Вс 22 • Сэ 22,

Аээ 21 = Ав 22 • Аэ 12 + Вв 22 • Сэ 12 + Ас 22 • Аээ 22 + Вс 22 • Сээ 22,

Сэ 21 = Св22 • Аээ 12 + Db 22 • Сээ 12 + Сс 22 • Аэ 22 + Dс 22 • Сэ 22, Сээ 21 = Св 22 • Аэ 12 + De 22 • Сэ 12 + Сс 22 • Аээ 22 + Dс 22 • Сээ 22.

Uk2 = AET 1 • Uh = AET2 • Uh ,(19)

Uk1 = AE • AET2 • Uh = AET1 Uh ,(20)

Ukm = A 29 • AET 2 • Uh = AUkt • Uh ,(21)

Ukt = A 29 • AET 2 • Uh = A Ukt • Uh ,(22)

1кт = C 29 • AET2 • Uh = CIkt • Uh ,(23)

Ih = (Cm • AUkt + Dm • CIkt) • Uh .(24)

В выражениях (13)–(23) обозначено:

Аэ 14 = Ami • Ah1 + Bm1 • Ch1, Сэ14 = Cmi • Ah1 + Dmi • Ch1,

Аэ 24 = Am 2 • Ah 2 + Bm 2 • Ch 2, Сэ 24 = Cm 2 • Ah 2 + Dm2 • Ch 2,

Аэ 13 = Ac 14 • Аэ 14 + Bc 14 • Сэ 14, Аээ 13 = Ab 14 • Аэ 24 + Вв 14 • Сэ 24, Сэ 13 = Сс 14 • Аэ 14 + Dc 14 • Сэ 14, Сээ 13 = Се 14 • Аэ 24 + Db 14 • Сэ 24, Аэ 23 = Ас 24 • Аэ 24 + Вс 24 • Сэ 24, Аээ 23 = Ав 24 • Аэ 14 + Вв 24 • Сэ 14, Сэ 23 = Сс 24 • Аэ 24 + De 24 • Сэ 24, Сээ 23 = Св 24 • Аэ 14 + De 24 • Сэ 14.

Аэ 12 = Ас 13 • Аэ 13 + Вс 13 • Сэ 13 + Ав 13 • Аээ 23 + Вв 13 • Сээ 23, Аээ 12 = Ас 13 • Аээ 13 + Вс 13 • Сээ 13 + Ав 13 • Аэ 23 + Вв 13 • Сэ 23, Сэ 12 = Сс 13 • Аэ 13 + Dc i3 • Сэ 13 + Св 13 • Аээ 23 + De i3 • Сээ 23, Сээ 12 = Сс 13 • Аээ 13 + Dc i3 • Сээ 13 + Св 13 • Аэ 23 + De i3 • Сэ 23, Аэ22 = Ав 23 • Аээ 13 + Вв 23 • Сээ 13 + Ас 23 • Аэ 23 + Вс 23 • Сэ 23, (27)

Аээ 22 = Ав 23 • Аэ 13 + Вв 23 • Сэ 13 + Ас 23 • Аээ 23 + Вс 23 • Сээ 23,

Сэ 22 = Св 23 • Аээ 13 + Db 23 • Сээ 13 + Сс 23 • Аэ 23 + Dс 23 • Сэ 23,

Сээ 22 = Св 23 • Аэ 13 + De 23 • Сэ 13 + Сс 23 • Аээ 23 + Dс 23 • Сээ 23.

Аээ 1 = Ас11 • Аэ 11 + Вс11 • Сэ 11 + Aeii • Аээ 21 + Ве11 • Сээ 21,

Аээв1 = Ас11 • Аээ 11 + Вс11 • Сээ 11 + Aeii • Аэ 21 + Ве11 • Сэ 21,

Сээ 1 = Сс 11 • Аэ 11 + Ddl • Сэ 11 + Се 11 • Аээ 21 + De ll • Сээ 21,

Сээв1 = Сс 11 • Аээ 11 + D dl • Сээ 11 + Се11 • Аэ 21 + De ll • Сэ 21,

Аээ 2 = Ав 21 • Аээ 11 + Вв 21 • Сээ 11 + Ас 21 • Аэ 21 + Вс 21 • Сэ 21, (29)

Аээв 2 = Ав 21 • Аэ 11 + Вв 21 • Сэ 11 + Ас 21 • Аээ 21 + Вс 21 • Сээ 21, Сээ 2 = Св 21 • Аээ 11 + De 21 • Сээ 11 + Сс 21 • Аэ 21 + Dс 21 • Сэ 21,

Сээв 2 = Св 21 • Аэ 11 + De 21 • Сэ 11 + Сс 21 • Аээ 21 + Dс 21 • Сээ 21.

А 27 = Аээ l - Аээв 2, А 28 = Аээ 2 - Аээв 1, С 27 = Сэн l + Сээв 2, С 28 = Сээ 2 + Сээв 1,

АЕ = А27-i • А28,

А 29 = Аээ 1 - АЕ + Аээв 1,

С 29 = С 27 • АЕ + С28,

АЕТ = Ат • А29 + Вт • С29.

Выводы. Таким образом, полученные матричные выражения (13)–(33) позволяют определить напряжения и токи в фазных координатах при аварийных режимах во всех точках фидера 35 кВ, содержащего двухцепную линию.

Список литературы Расчет аварийных режимов фидера 35 кВ с двухцепной линией

Аржанников Е.А., Чухин А.М. Методы и приборы определения мест повреждения на линиях электропередачи. -М.: Энерго-пресс, 1998. -87 с.
Солдатов В.А., Чебесов Е.А. Критерии определения вида аварийного режима в се-тях 0,38 кВ при использовании отношений напряжений и токов//Вестн. КрасГАУ. -2016. -№ 8. -С. 104-110.
Солдатов С.В. Совершенствование мето-дов расчета и обнаружения аварийных ре-жимов сельских электрических сетей 10 кВ по наведенным напряжениям: автореф. дис.. канд. техн. наук. -М: Изд-во ВИЭСХ, 2015. -24 с.
Солдатов В.А., Яблоков А.С. Исследова-ние наведенных напряжений на проводнике под линией электропередачи 35 кВ//Акту-альные проблемы науки в агропромышлен-ном комплексе: сб. ст. 66-й Междунар. науч.-практ. конф.: в 3 т. Т. 2/Костромская ГСХА. -Караваево, 2015. -С. 193-196.