Расчет характеристик ускоренного движения автомобиля по дороге со случайным микропрофилем

Как правило, механические и математические модели систем автомобилей формируются в форме сложных многомассовых колебательных систем [1]. Из-за дорожного возбуждения транспортные средства (ТС) могут подвергаться сложной вибрации, что неблагоприятно для здоровья пассажиров и сохранности товаров. Поэтому важными и актуальными задачами являются оценки и контроль колебаний транспортных средств в пределах комфортной зоны, чтобы обеспечить безопасное рулевое управление и физическое здоровье водителей и пассажиров, а также стабильность работы системы человек-автомобиль-дорога. В процессе движения автомобиля случайное и изменчивое дорожное покрытие является основным фактором, вызывающим вибрацию автомобиля. Таким образом, исследование стохас-

тической вибрации транспортного средства, вызванной дорожным возбуждением, является серьезной проблемой при проектировании транспортного средства и моделировании его характеристик.

Наряду с учетом нерегулярности дорожного полотна [2] уже давно признано необходимым принимать во внимание и запаздывание воздействия случайного микропрофиля на одну или несколько пар задних колес ТС относительно передних [3,4]. Еще недавно динамика как в линейной, так и нелинейной постановке изучались без учета протяженности ТС, а следовательно, и эффекта запаздывания [5]. Дело в том, что этот учет является нетривиальной задачей, так как запаздывание превращает стохастическую систему в немарковскую. Но в широком диапазоне скоростей пренебрежение запаздыванием приводит к завышению дисперсии ускорения подрессоренной массы, особенно на резонансной скорости движения. С другой стороны, в работе [6] показано, что введение в модель управляющего устройства временного запаздывания между передними и задними колесами улучшает динамические характеристики ТС.

Для анализа движения ТС с переменной скоростью используется алгоритм, представленный в работах [7,8].

1.    Модель ТС

Рассмотрим движение ТС в вертикальной плоскости. Схема этого ТС изображена на рис.1, состоит из движущейся массы т, подвешенной на двух колесах и моделируется системой с двумя степенями свободы. Предполагается, что в процессе движения подвеска остается вертикальной.

Обозначим через Y ( t ) смешение центра масс из положения статического равновесия (соответствующего у о), а через & ( t ) - угол наклона корпуса ТС ( t - время). Пусть U = U ( s ) - функция, характеризующая профиль дороги ( s = r ( t ) - пройдет ihih путь). G - центр масс, ki и ci - коэффициенты жесткости и демпфирования ( i = 1 , 2). Тогда уравнения движения будут иметь вид [5]:

mY(t ) + c 1 Z i + c 2 Z 2 + k 1 Z i + k 2 Z 2 =

= mg,(1)

• ■ V                                  ■■

• I& + C 1 1 1 Z 1 - C 2 1 2 Z 2 + k 1 1 1 Z 1 -

• - k 2 12 Z2 = 0,( 2 )

где I - момент инерции ТС относительно центра масс, g - ускорение свободного падения, а точками обозначены производные по времени.

Из уравнений (1), (2) следует, что в состоянии покоя ( I = 1 1 + 1 2)

ℓ2 m g        ℓ1 m g z10 = ~lkT ’ z20 = ~1кГ ’ а следовательно,

12 z 10 +11 z20   mg с 12 , Ih y0 = I = 12 \k1 + k2) ’ q0 = z 10 — Z20 = mg ^ 12 - 11 j

y ( t ) = ¹ 2 [ ^Z 1⁽ t )⁺ U 1⁽ t )] ₊

1 1 [ Z 2( t )+ U 2 ( t )]

⁺             I              y 0 ,

& ( t ) = ^Z 1⁽ t ) ^{+ U} 1⁽ t ) — ^Z 2⁽ t ) — ^U 2⁽ t ) _- Q 0

где

U1( t ) = U(s 1( t)),      U2( t ) = U(s2( t)), s2(t) = s 1(t) - I, откуда следует, что

^Z 1⁽ t ) = y 0 ^{+ Y (} t ) ^{+ 1} 1 [ ^Q 0 ⁺ & ⁽ t )] ^- U 1⁽ t ) ,

^Z 2⁽ t ) = y 0 ^{+ Y (} t ) ^{- 1} 2 [ ^Q 0 ⁺ & ⁽ t )] ^{- U} 2⁽ t ) •

Это позволяет записать уравнения (1), (2) в виде:

X 1( t ) = X 2 ( t ) ,

X 2( t ) =

• ^-    ( ^c 11 ^{+ c} 12) X 2( t ) ^- ( ^c 11 ¹ 1 ^{- c} 12 ¹ 2) X 4⁽ t ) ^-- ( ^k 11 ^{+ k} 12) X 1⁽ t ) ^- ( ^k 11 ¹ 1 ^{- k} 12 ¹ 2) X 3⁽ t ^{) +} + c 11 U 1( t ) + c 12 UJ 2( t ) + k 11 U 1( t ) + k 12 U 2( t ) , X 3 ( t ) = X 4 ( t ) ,                                 (3)

X 4( t ) =

• ^-    ( ^c 21 ^{+ c} 22) ^X 2⁽ t ) ^- ( ^c 21 ¹ 1 ^{- c} 22 ¹ 2) ^X 4⁽ t ) ^-- ( k 21 ⁺ k 22) ^X 1⁽ t ) ^- ( ^k 21 ¹ 1 ^{- k} 22 ¹ 2) ^X 3⁽ t ^{) + + c} 21 ^U 1⁽ t ) ^{+ c} 22 ^U 2⁽ t ) ^{+ k} 21 ^U 1⁽ t ) ^{+ k} 22 ^U 2⁽ t ) •

где

• ^c 11 = —, ^c 12 = —,  k 11 = —,  k 12 = —,

mmmm c1 ℓ1

c 21 =        c 22 = k1 ℓ1

k 21 =         k 22 =

Форма фильтра, формирующего неровности пути, выбрана в виде [9]:

U‘‘ ( s ) +2 a U‘ ( s ) + w ² U ( s ) = g 0 V * ( s ) , g 2 =4 aw ² a 0 ,

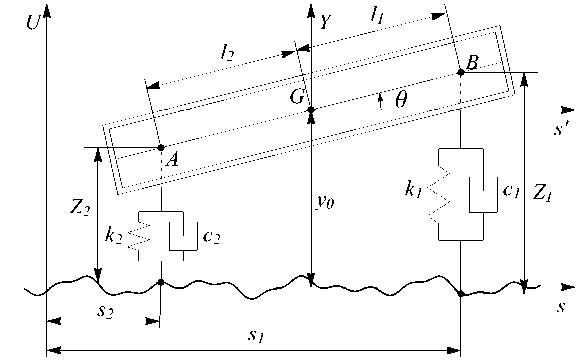
Рис. 1

где V* ( s ) - белый шуг i переменной s. При этом отклик U ( s ) будет иметь ковариационную функцию

K u ( s ) = а 0 e

~^alsl (cos ш о s + — sin ш о |s| ) , ω 0

ш2 = ш 2 + а2, где а о = const - стандарт микропрофиля до роги.

Если перейти в уравнении фильтра от переменной s к времени t в предположении, что s = r ( t ) - монотонно возрастающая функция времени ( s = v ( t ) >  0), то система стохастических обыкновенных дифференциальных уравнений (СОДУ), представляющая преобразованный фильтр, будет иметь вид:

■ U1(t) = Ц2И ф (t) ’ (4) ■ U2 (t) = 2aU2(t) + ш2 Ui(t) Ф (t)               1 . ~^= V (t), /Ф(t) где V(t) - случайный процесс типа белого шума единичной интенсивности, t = ^(s), Ф ( t ) = / ( s )| s=г (t )

В случае постоянного положительного ускорения a = а о >  0 и анализа периода разгона ТС скорость движения v ( t ) выразится «формулой v ( t ) = а о t + v о ( v о = const, t > 0). а система уравнений фильтра (4) принимает следующий вид:

U Z1( t ) = к( t ) U 2( t ) ,

UU 2( t ) = — к( t ) [2 aU 2 ( t ) + ш ² U 1 ( t )] + (о)

+ gо /к(t) V(t), причем (sо = const)

s = r (t) = 02° t2 + v о t + s о, t = ^(s) = —vо + /vо + 2 aо (s — sо) a0                 ,

/ ^{( s} ) = /2 / / a = “7Д = Ф ⁽ t ) ’

У v о + 2 а о ( s — s о) ^к( t )

k( t ) = У а о t ² + 2 а о v о t + v 2 = а о t + v о .

Обозначая U 1( t ) nej>ез X 5( t ). a U ₂( t ) через X 6( t ) и ограничиваясь последним случаем переменной скорости ТС, запишем уравнения движения в матрично-векторной форме:

X ( t ) = Q ( t ) X ( t ) + H ( t ) X ( t — T )

+ G ( t ) V ( t ) ,   t> 0  ( 1 1 =0) ,      ( 6 )

где t = l/v ( t ),
	■ 0 1 0 0      0          0
	q 21 q 22 q 23 q 24     k 11         c 11
	0001  0   0
Q ( t ) =
	q 41 q 42 q 43 q 44     k 21         c 21
	0 0 0 0      0         k( t )
	_ 0 0 0 1 — k( t ) ш 2 — 2 k( t ) a
		■00000 0 ’
		0 0 0 0 k 12 c 12
		00000 0
H ( t ) =		0 0 0 0 k 22 c 22 ’
		00000 0
		0000 0 0

G (t) =[0 0 0 0 0 g о y/Kd ]T, q 21 = — (k 11 + k 12), q 22 = - (c 11 + c 12), q23 = — (k 11 11 — k 12 12), q41 = — (k21 + k22), q24 = — (c 11 11 — c 12 12), q42 = — (c21 + c22), q43 = — ( k 21 11 — k 22 12), q44 = — (c 21 11 — c 22) 12).

2.    Метод и результаты исследования

Для исследования поведения ТС использовалась модификация схемы, сочетающей метод шагов и расширение пространства состояний [10]. Для ее применения переменное запаздывание т ( t ) приближенно заменялось кусочно-постоянным т(t ) со "ступеньками", длина которых кратна величине т* (выбор т* определяется необходимой точностью ап-прокспмащш т ( t )).

Для финализации подготовки расчетов необходимо задать начальные условия для расчетов. Эти условия будут выглядеть так: предположим, что при t <  0 состояние ТС характеризуется соотношениями X 1( t ) = X ₂( t ) = X з( t ) = X ₄( t ) = 0. выходные переменные фильтра X 5( t ) и X 6( t ) находятся в стационарном состоянии, имея совместное нормальное распределение с параметрами

Е [ X 5( t )] = Д X б( t )] = 0 , Е [ X 2( t )] = а 2 ,

Е [ X 5( t ) X б( t )] = 0 , Е [ X 2( t )] = а 2 ш ² .

Все это позволяет считать матрицы Q q, H о и G о [Ю] нулевыми.

Многошаговый численно-аналитический алгоритм вычисления искомых характеристик был реализован с помощью пакета Ма-thematica, обладающего мощным командным языком высокого уровня со всем необходимым инструментарием (в нашем случае это средства для проведения длинных аналитических выкладок, работы с символьными строками, списками объектов различных типов и рациональной арифметикой, построения графиков таблично заданных функций, численного решения систем ОДУ, вывода результатов символьных преобразований на дисплей в обычной математической форме и итогов расчетов на внешний носитель, интерактивного и пакетного режимов работы и др.), и состоял из циклической последовательности следующих шагов:

• -    расширение вектора состояния, формирование списка новых первых моментов и подготовка начальных условий;

• -    символьное построение системы ОДУ для векторной функции математических ожиданий и матрицы функций ковариации;

• -    численное интегрирование построенной системы ОДУ;

• -    сохранение результатов вычислений в конце каждого шага длиной т для дальнейших вычислений.

Таблица 1

N	Дорога	а 2 • 10 4 (м 2)	α	ω 0
1	Грунтовая	2.3	0.0148	0.03342
2	Асфальтовое шоссе	1.0	0.0500	0.60000
3	Булыжное шоссе	3.2	0.3000	1.00000

Таблица 2

N	m (кг)	c 1 (нс/м)	c 2( нс/м)	k 1(н/м)
1	17800	80000	80000	4.00-106
2	13200	16000	18000	4.65-105
3	8444	9080	9080	2.72-105
N	k 2(н/м)	1 (к юм 2)	1 1(м)	1 2(м)
1	4.00-106	930.0	2.000	2.000
2	5.24-105	3000.0	2.340	2.885
3	8.53-105	12446.2	2.590	3.290

Таблица 3

Автомобиль ( k)	Номер фазовой координаты ( i)
	1	2	3	4
I	2	5	8	11
II	3	6	9	12
III	4	7	10	13

Параметры дорожного микропрофиля выбирались из табл. 1 [11], а ТС - из табл. 2 [5,12-14].

Движение же рассматривалось равноускоренным, причем в начальный момент времени скорость составляла 8 м/с. Ускорение было выбрано так, чтобы к концу третьей секунды скорость была равной 16 м/с. Элементарное запаздывание вычислялось делением расстояния между колесами автомобиля на конечную скорость и еще на константу, в качестве которой в расчетах использовалось значение 4. При этом начальное множество совпадало с отрезком [—8 т*, 0], что потребовало задавать нулевыми мат-рипы Q о( t). H q( t) 11 G q( t) на 8 шагах, а на основном участке до достижения времени движения в 2 с для первого автомобиля требовалось осуществить расчеты на 32 этапах, для второго - на 25, а для третьего - на 22. Соответствующие значения т* равнялись 0.0625 с, 0.0816406 с и 0.091875 с.

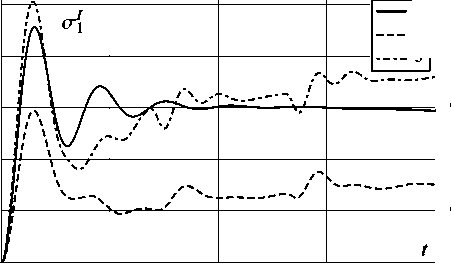
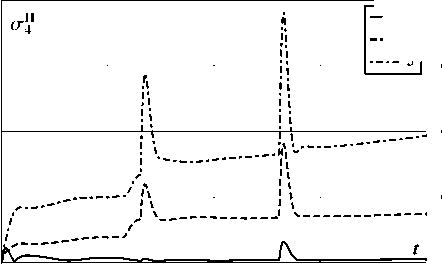
На рис. 2-13 показано поведение функций среднеквадратичных отклонений ok(t) случайных функций Xi(t) ii = 1, 2, 3, 4; k = I, II, III). Графики соответствующих мате матических ожиданий mi (t) также не представлены, так как при выбранных начальных условиях они не изменялись. Соответствие номеров рисунков выбору характеристик автомобиля и номеру фазовой координаты приведено в табл. 3. На этих рисунках класс дороги отмечен цифрой от 1 до 3.

0.025

0.02

0.015

0.01

0.005

0.5

1.5

Рис. 2

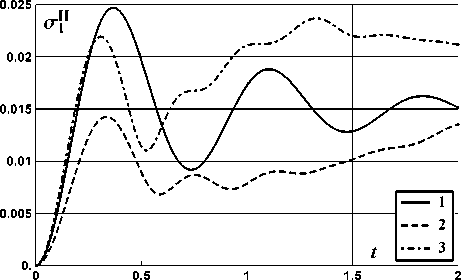
Рис. 3

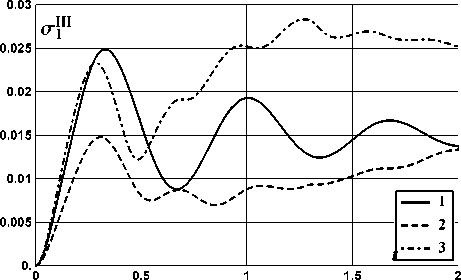
Рис. 4

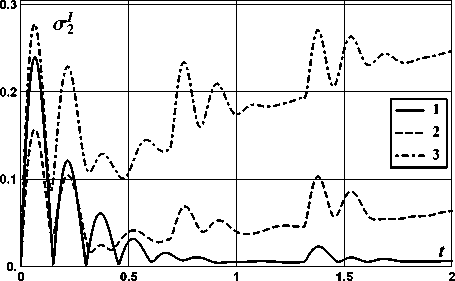
Рис. 5

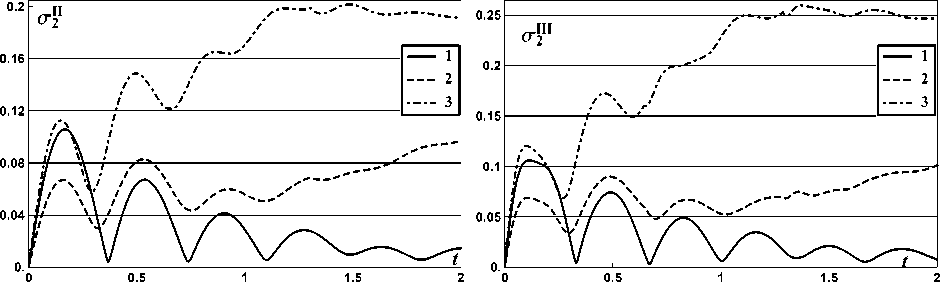
Рис. 6                                              Рис. 7

3.    Заключение

Несложно увидеть, что поведение полученных для переменной скорости средних квадратичных отклонений существенно отличается от поведения этих же характеристик в случае постоянной скорости [15].

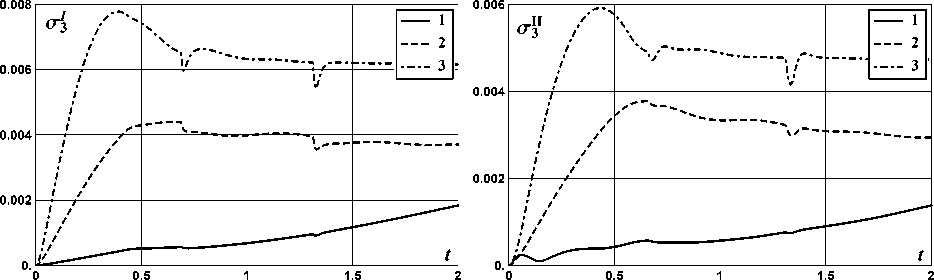
Рис. 8                                              Рис. 9

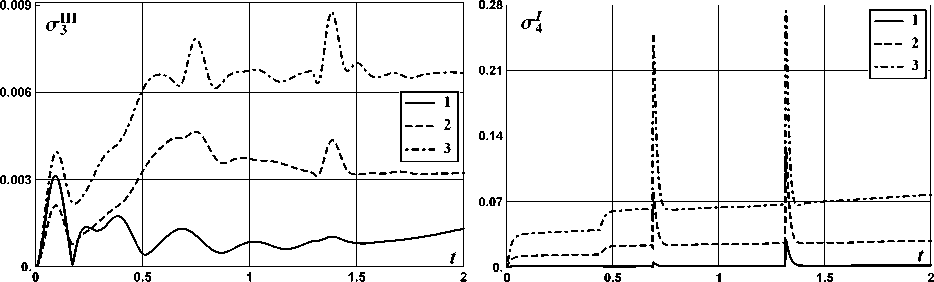
Рис. 10                                             Рис. 11

0.12

0.09

0.06

0.03

0.5

1.5

Рис. 12

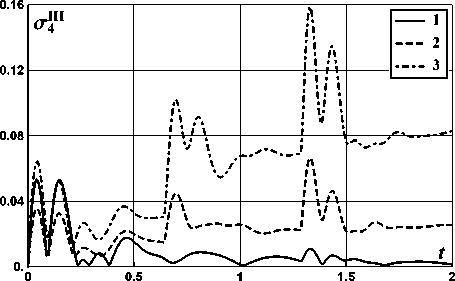
Рис. 13