Расчет минимальной величины вспомогательного заднего угла резца при точении цилиндрических поверхностей с некруглыми направляющим

В машиностроении применяются детали, поверхности которых относятся к классу цилиндрических поверхностей. В качестве направляющих линий таких поверхностей среди прочего используются кривые, описываемые в полярной системе координат уравнением [1,2]

р(\рг) = а — Ьсоз(пц/), (1) где я - средний радиус синусоиды, b - эксцентриситет, п - количество осей симметрии кривой.

Одним из способов получения указанных поверхностей является точение или растачивание резцом. При этом резцу наряду с движением подачи Ds вдоль оси заготовки сообщается радиальное движение Drp по закону Д(у) = ecos(n\|/) посредством щупа, жестко связанного с резцом и опирающемуся на требуемое копирное устройство, причем щуп располагают оппозитно получаемой поверхности [3-5]. Одновременно с перемещениями резца заготовка совершает вращательное движение вокруг своей оси, обеспечивая главное движение резания Dr (рис. 1).

Рис. 1. Схема обработки: 1 - щуп, 2 - резец, 3 - заготовка, 4 - копир

Одной из проблем при реализации такой операции обработки является правильная заточка инструмента, так как при повороте детали на некоторый угол т в процессе обработки проекция инструмента на плоскость, перпендикулярную рабочей плоскости, может пересекать сечение получаемой поверхности, что приведет к браку изделия и поломке резца (рис. 2).

Рис. 2. Расположение сечений резца и детали: а - в начальный период обработки;

б - при повороте на угол т

В связи с этим возникает задача определения предельного угла наклона проекции линии пересечения главной и вспомогательной задних поверхностей на плоскость, перпендикулярную рабочей. При исследовании процесса было замечено, что искомый угол при обработке внутренних поверхностей больше, чем при обработке наружных, поэтому задача может быть сведена к определению предельного положения точки радиального профиля детали на высоте, равной высоте державки резца. Для решения этой задачи найдем уравнение семейства профилей детали при ее формообразующем движении относительно вершины резца.

В декартовой системе координат указанная кривая (1) запишется следующим образом:

[Х = p(w)cosw;

(Y = p(v) sin Ц/-

Поскольку заготовка, а с ней и данный профиль, вращаются, то при повороте декартовой системы на угол © новые координаты будут определяться как

X] = p(\p)cosv cos©-p(\y)cos\y sin®;

• Y[ = р(х|г) sin и sin со + p(\y) cos \p cos m.

Вынося p(v) за скобки и преобразуя по известным тригонометрическим формулам, полу чим:

Xt = р(\р) cos(y + ю);

Yj = р(ц/) sin(y + ®).

Как отмечалось ранее, в реальной обработке резец перемещается в горизонтальной плоскости по закону, обеспечивающему формирование синусоидального профиля, при одновременном вращении заготовки. В данном случае примем резец неподвижным в соответствующей неподвижной системе координат, а заготовке сообщим необходимое движение вдоль оси абсцисс. Тогда, с учетом подстановки в (4) значения радиус-вектора из (1), получим

• X, = (а - b cos(my) cos(\g + ©) + b cos(n®);

Yj = (a - b cos(n\y) sin(\pr + ©).

Пусть высота державки резца в радиальной плоскости, проходящей через его вершину, равна h (рис. 3). Тогда из второго уравнения системы (4), зная, что Yj = -h , найдем взаимосвязь угла поворота профиля © с величиной h и углом поворота радиус-вектора у :

(a-bcos(m|/))

Подставляя (6) в первое уравнение системы (5), получим:

Xj ™(a-bcos(n\yj) cos

arcsin

' -h ) va-bcos(m|/))

+ bcos

I . ( -h ] n arcsin ------------- -\p l 1^а-Ьсо8(п\|/))

Щуров И.А., Ворона В.В. Расчет минимальной величины вспомогательного заднего угла резца при точении цилиндрических поверхностей с некруглыми направляющими

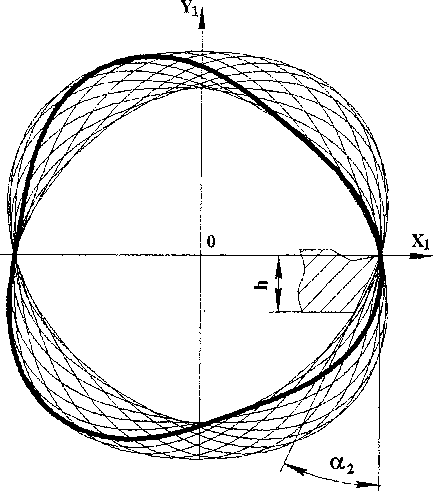
Рис. 3. Семейство кривых (а=40, Ь=4, л=3) по системе (5) и положение резца

Из уравнения (7) можно найти такое значение величины ц/, когда Xj будет иметь минимальное значение в одной из координатных полуплоскостей. Экстремальное значение X, можно получить, например, протабулировав (7) или определяя производную по у .

Обозначив

F(\y) = arcsin

-h a-bcos(my)) ’

выражение (7) можно свести к виду

Xj = (а-Ьсоз(пф) cos(F(v/)) + bcos(n(F(\|/)-y)) .

Тогда экстремальное значение X; находится из выражения б^а cos (F(v)) - b cos(n\y) cos (F(y)) + b cos (n (F(y) - ф)^

Дифференцирование по 7 в последнем уравнении не представляет собой математической трудности, однако является достаточно громоздким и здесь не приводится. Полученное уравнение является трансцендентным относительно у и решается на ЭВМ.

Определив из (8) значение угла ц/, после подстановки в (6) и далее в (5) находятся значения координат точек профиля, по которым затем рассчитывается значение предельного угла инструмента в радиальной плоскости:

а2 = arctg

Y,

Расчет предельного угла а2 позволяет определить зависимость между задними углами а, а; и углами в плане ф, 9j по уравнению tga■sinф1

tga2—7---Y а, = arctg

ЗПЦф + фД

1 tgф1■COSф созф] зт(ф + ф1)

В одном из случаев обработки растачиванием детали ЦСКБ «Прогресс» г. Самара (а = 10, b = 0,625 , п = 3) для ряда высот державок резцов h был рассчитан ряд значений предельных радиальных углов а2. Результаты расчета приведены в таблице.

Значения предельных углов а2 при растачивании детали

h, мм	3	4	5	6	7	8
а2, град	19,15	22,1	24,86	28,18	31,56	35,63

Таким образом, была установлена взаимосвязь предельного угла наклона проекции линии пересечения главной и вспомогательной задних поверхностей на плоскость, перпендикулярную рабочей, и высоты державки резца при обработке некруглых цилиндрических поверхностей синусоидального профиля с базированием щупа, связанного с резцом, по поверхности копира оппозитно поверхности детали.

В ходе исследования процесса токарной обработки рассматриваемой цилиндрической поверхности были сделаны следующие наблюдения:

• -    при увеличении высоты державки резца предельный угол возрастает;

• -    с уменьшением эксцентриситета b при постоянных а, п и h предельный угол уменьшается;

• -    с увеличением количества осей симметрии п при постоянных а, b и h предельный угол увеличивается;

• -    с увеличением среднего радиуса а при постоянных n , b и h предельный угол уменьшается;

• -    если геометрия профиля соответствует рекомендациям, приведенным в работах [1, 2], то с увеличением количества осей симметрии п при постоянных среднем радиусе а и высоте державки предельный угол уменьшается.