Расчет оболочечных конструкций, применяемых в сельском хозяйстве

В сельскохозяйственном производстве силосами называют глубокие бункерные хранилища сыпучих материалов цилиндрической или призматической формы с высотой, доминирующей по отношению к поперечному размеру (рис. 1).

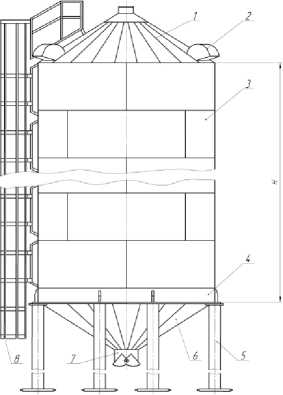
Рис. 1.

1 – кровля; 2 – вентиляционный люк; 3 – корпус; 4 – кольцевой шпангоут; 5 – опорная колонна; 6 – выгрузная воронка; 7 – затвор; 8 – лестница шахтная; Н – высота цилиндрического корпуса.

Как правило, материалом конструкции является металл. Однако, в последнее время, все шире применяются композиционные материалы, имеющие неоспоримые преимущества. Так, широкое распространение получают трехслойные оболочечные элементы (так называемые «сэддвич панели»). Этот современный строительный материал, состоит из нескольких слоев различных материалов, у каждого из которых есть свое функциональное предназначение.

При расчете трехслойных панелей и оболочек на общую устойчивость и на поперечный и продольно-поперечный изгиб решаются те же задачи, что и при расчете однослойных панелей и оболочек. В случае легких маложестких на сдвиг заполнителей используют известные [3] расчетные формулы, полученные с учетом взаимных смещений внешних слоев вследствие деформации сдвига заполнителя (в случае заполнителей с большой жесткостью сдвига эти формулы переходят в известные формулы для однослойных панелей и оболочек при соответствующих жесткостных характеристиках составных сечений).

В формулы для расчета панелей и оболочек па общую устойчивость и изгиб входят приведенные упругие параметры заполнителя. В случае сплошного заполнителя из однородного материала — например, из пенопласта — этими приведенными упругими параметрами являются параметры материала заполнителя. Для заполнителей из ребристых конструкций (сотового, типа гофра или складчатого и др.) или из армированного пенопласта используются упругие параметры — это параметры эквивалентного в отношении работы панели на общую устойчивость или изгиб сплошного однородного заполнителя.

Так как трехслойные панели и оболочки образованы из тонкостенных элементов, то элементы панелей рассчитывают на местную устойчивость по известным формулам [3].

В некоторых случаях возможно использование панелей, работающих и после того, как отдельные их элементы (например, элементы сот или ребра, армирующие пенопласт) теряют местную устойчивость. В этих случаях расчет (в частности, при определении приведенных упругих параметров) ведут с учетом такой работы элементов. Однако местная потеря устойчивости элементов может привести к исчерпанию несущей способности всей панели. Поэтому, помимо расчета панели на общую устойчивость, необходимо проверять устойчивость, связанную с исчерпанием ее несущей способности при местной потере устойчивости элементами [3].

Часто, применяемая в сельском хозяйстве конструкция имеет в поперечном сечении не круглое (не каноническое) сечение (рис.2). На сегодня расчет таких конструкций (определение НДС и критических нагрузок) проводится в рамках метода конечных элементов. Но практика требует более простые расчетные формулы, которые могут быть получены в результате синтеза теории и эксперимента (моделирования).

Процесс моделирования основан на рассмотрении физически или механически подобных явлений. Так для подобия двух явлений необходимо и достаточно, чтобы численные значения определяющих безразмерных параметров, образующих базу, в этих двух явлениях были одинаковы.

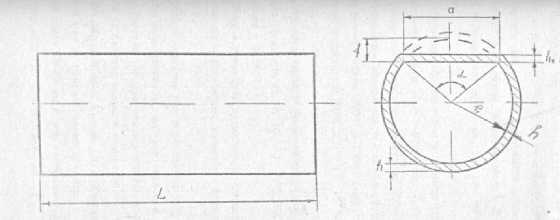
Рис. 2.

Для описания того или иного явления используются физические величины, связанные между собой функциональными зависимостями, характеризующими данное явление. Если некоторые из этих величин принять за основные и установить для них единицы измерения, то единицы измерения всех остальных величин могут быть определенным образом выражены через единицы измерения основных. Если размерные физические величины зависят от выбора системы единиц, то функциональные зависимости, описывающие процесс, не должны зависеть от выбора этой системы и обязаны обладать некоторой структурой. Эта структура устанавливается в соответствии с теоремой, на основании которой любая функциональная зависимость, описывающая физический процесс, может быть представлена в виде соотношения между безразмерными комплексами или параметрами. Чем меньше число параметров, управляющих изучаемым явлением, тем больше ограничена форма функциональной зависимости и тем проще вести исследование. Если число основных единиц измерения равно числу определяющих параметров, имеющих независимые размерности, то эта зависимость определяется с точностью до константы, которая достаточно просто определяется экспериментально [1].

Функциональная зависимость для составной ортотропной цилиндрической оболочки в случае осевого сжатия в безразмерном виде может быть выражена следующим образом

P*=Pорт φ(α/π), где

φ(α/π) – функция учитывающая влияние угла α составной оболочки на ее несущую способность,

Pорт – значение критической нагрузки для ортотропной круговой цилиндрической оболочки в безразмерном виде.

Экспериментальное исследование напряженно-деформированного состояния проводилось на оболочках неканонической формы (рис.3), выполненных из ортотропного материала. Отношение E 1 / E 2 = 0,64 (E 1 - определялся вдоль образующей, а E 2 – перпендикулярно ей).

Нагрузка, в виде осевой силы P орт , прикладывалась к торцам оболочки (рис. 3) с эксцентриситетом Z через торцевые пластины (рис. 4).

Осевая критическая сила определялась по формуле

P орт =c 0 2π/ 3^0,5 (E 1 E 2 /(1-μ 1 μ 2 ))^0,5 h².

Функция безразмерного параметра [2] φ(α/π) =1,028 + 0,550 α/π.

С увеличением размеров среза величина критического продольного усилия общей потери устойчивости уменьшается.

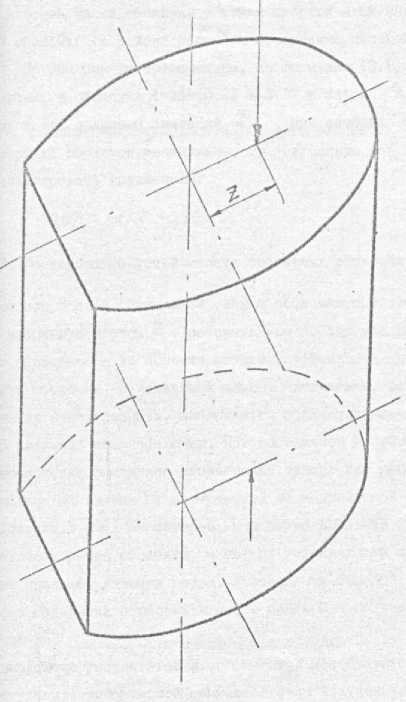
Рис.3.

Рис. 4.

статической устойчивости ортотропных составных оболочек. – Проблемы механики оболочек.     Калинин,     Калининский политехнический институт (Калининский государственный университет). 1988, с.51.

Прочность устойчивость колебания — М.: Машиностроение, 1968. — 464 c.

Резюме

Процесс моделирования основан на рассмотрении физически или механически подобных явлений. Так для подобия двух явлений необходимо и достаточно, чтобы численные значения определяющих безразмерных параметров, образующих базу, в этих двух явлениях были одинаковы.

Dogadkin V. N. Summary

The modeling process is based on consideration of physically or mechanically such phenomena. So for the similarity of the two phenomena is necessary and sufficient that the numerical values of the governing dimensionless parameters, which form the base, those two things were the same.