Расчет процесса фракционирования порошка в роторе трубчатой центрифуги

DOI:

Центрифуги получили широкое распространение в процессах очистки масел, а также при создании вакцин и сывороток в фармацевтической промышленности, где используют центрифуги марок ОТР-102К-01 и ОТР-151К-01 – машины периодического действия с осветляющим трубчатым ротором [13–20]. С целью осветления суспензий с мелкодисперсной твердой фазой концентрацией не более 2%, и отношением плотностей твердой и жидкой фаз в диапазоне не менее 1,1, предназначены центрифуги марки РТР – 102К – 01.

Помимо этого, трубчатые центрифуги используют и для дисперсионного анализа высокодисперсных систем, а также в случаях, когда необходимо применять машины с малыми рабочими поверхностями. В частности, центрифуги марки ОТР, РТР применяют для осветления суспензий с тонкодисперсной твердой фазой с размером частиц в диапазоне 0,5 – 5 мкм, объемная концентрацией их в жидкой фазе не более 1%.

Диаметры роторов промышленных центрифуг – 80 – 150 мм, лабораторных – 40 – 50 мм; производительность – 0,2 – 2 м3/ч. Данный тип машин используют в пищевой, химической, медицинской и других отраслях промышленности.

Следует отметить, что вследствие сравнительной простоты изготовления и надежности в эксплуатации за истекшие 30 лет технические параметры трубчатых центрифуг (диаметр и длина ротора, фактор разделения) практически не менялись.

Sediment

Suspension

Fugate

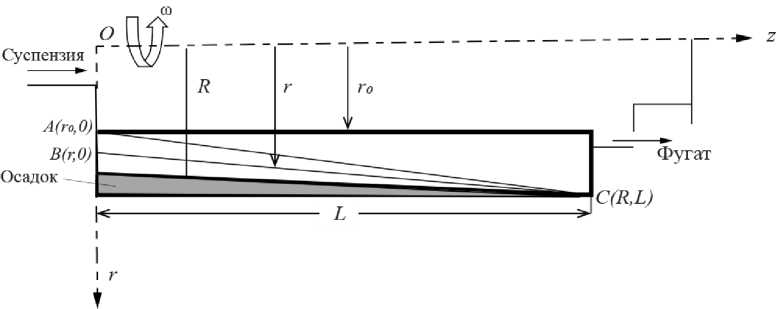
Рисунок 1. Схема ротора трубчатой центрифуги непрерывного действия (в меридиональном сечении)

В теоретическом плане проблема количественного анализа кинетики процесса разделения смесей, применительно к газовой центрифуге, исследовалась в работах [6–12], к жидкостной центрифуге – в работах [1–5]. Несмотря на это, такие вопросы как эволюция дисперсности взвеси при обработке ее во внутрироторном потоке, формировании слоя осадка на стенке ротора, оптимизации процесса центрифугирования и другое проработаны все еще недостаточно.

В связи с этим данная проблема нуждается в дальнейшем углубленном изучении, поскольку в практическом отношении необходимо располагать корректным расчетным аппаратом прогнозирования протекания данного процесса.

Ниже, с новых позиций, предлагается аналитический аппарат в известной степени свободный от отмеченных недостатков и численное моделирование процесса разделения суспензии с целью фракционирования затравочного порошка в рабочем объеме центробежной машины непрерывного действия, относящейся по типу к отстойной центрифуге.

В дальнейшем при анализе процесса седиментации взвеси в роторе центрифуги предполагают, что обрабатываемая суспензия представляет собой слабо концентрированную жидкостную смесь, включающую частицы малого размера и примерно сферической формы. Считают, что ротор центрифуги находится в равномерном движении с угловой скоростью ω , поток ограничен областью r 0 ≤ r ≤ R (где r 0 и R , соответственно, радиус свободной поверхности жидкости и радиус ротора), 0 ≤ z ≤ L (рисунок 1).

• Figure 1.    Diagram of the rotor of a continuous tubular centrifuge (in the meridional section)

  По данным ряда работ установлено, что значение числа Рейнольдса во внутрироторном потоке центрифуги в таких случаях невелико. Поэтому режим течения в роторах этих машин следует считать ламинарным. Это создает предпосылки для количественного анализа в аналитической форме кинетики взвеси в потоке, с использованием известной, справедливой для тонкодисперсного порошка, зависимости [2]

  
  

  ω ² r Δ δ ²

  
  

  υ =         ,

  ⁰    18 µ

  
  
  
  

  где Δ = ρ т – ρ ж , ρ т , ρ ж – соответственно, плотность твердого и жидкости, кг/м³; и для определенности ρ т >  ρ ж , Δ > 0; µ – динамическая вязкость жидкости, Па ⋅ с; δ – диаметр частицы, м; v 0 = v r – характерная скорость частицы (м/с).

  
  

В свою очередь, осевая составляющая скорости потока выбирается по зависимости [2]

V

° z =^ пр

R ² -

- + r ₀²ln ^f—

⁰ I R

где 44

в = — + -0- - R² r - r , м⁴; (3) V - расход жидкости, м³/с; V = Q /3600, Q - производительность центрифуги, м³/ч.

В таком случае, исходя из дифференциального уравнения траектории пробной частицы dr/dz = иг/и , с учетом (1)-(3) приходят к соотношению

18 ^ V

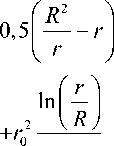
dr = пвю ² А д² dz . (4)

Для того чтобы получить зависимость между параметрами потока жидкости и пробной (гипотетической) частицей, перемещающейся по траектории ВС (где В ( г, 0), С ( R, L )), уравнение (4) интегрируют слева по r в пределах от r до R , справа по z - в пределах от 0 до L (рисунок 1).

В результате чего получают выражение для так называемого критического диаметра данной частицы

д (r, ю с о ) = ^ ^ yV (c о) I (r),       (5)

где обозначено

9R      -3 -i

Y =--------, м³с 1 ;

2neL А l (r) r2

- R ² + 2 R ² In [ R ] - 2 r 2 ln^{2 f} R ]

У r J         ( r J

м

2;

P рассчитывают по (3).

Величина 5 к = 8 к ( r 0 ) - называемый глобальным критическим диаметром - т. е. диаметр частицы, перемещающейся по траектории AC (рисунок 1) ( ВС - траектория частицы текущим диаметром 5 ).

Пусть F(д) - счётная функция распреде- ления частиц, такая, что / х n (д < д

F ( д ) = ^-----) ,

n0

где n - количество частиц размером д < д', n0 - количество частиц в исходной суспензии, 5’ вычисляется по (5).

В принятом допущении о невысоком значении концентрации твердой фазы в исходной суспензии, согласно результатам [2], коэффициент е уноса рассчитывается по формуле

^£ = n = R^ I'^{( д} < ^r ) ) r ⁽⁷⁾

В свою очередь, коэффициент осветления - относительное число частиц в осадке -вычисляется по зависимости n = 1RФ(д(r))rdr , R '0 0

где Ф ( д ) = 1 - F(д'), Ф ( д ) - так называемая характеристическая функция, F(д) определяют согласно (7).

Причём, очевидно, что величины s и п , по определению, связаны соотношением s + п = 1.

Материалы и методы

Объектом исследования являлась (условно) суспензия типа «жидкостная фаза + частицы» затравочного материала с полидисперсной твердой фазой затравки примерно сферической формы. Чтобы путём расчёта выделить из суспензии взвешенные в ней частицы заданного целевого диапазона твердую фазу подвергали процедуре фракционирования, используя для этой цели трубчатую центрифугу.

Расчеты проводили (в дополнение к данным расчетного примера к формуле (2)) на базе параметров: радиус свободной поверхности жидкости r 0 = 0,015 м; производительность по исходной жидкости Q = 0,2; 0,4 м³/ч; динамической вязкости р = 0,01; 0,04 Па - с; начальная счётная концентрация твердой фазы в суспензии с 0 = 0,01 = 1%.

В качестве массовой функции распределения твердой фазы в исходной суспензии выбирали (для простоты, по соглашению)

F (д ) = |?/д“ при^ " д"” (8)

⁰^ Ц при ^д > ^д тах , где, д пах = 10^-5 м.

Предполагается, что пробная двухфазная жидкостная система (типа сахарного утфеля) с объемной концентрацией с 0 твердого и заданной счётной функцией F ( 5 ) распределения твердой фазы по крупности равномерно перемешана в этой системе, причем плотность p i твердой фазы превышает плотность p жидкостной фазы.

Требуется, обрабатывая эту суспензию в центробежной машине, получить с её помощью частицы размером д е ( д 1 , д 2 ), где д 1 , д 2 -соответственно - наименьший и наибольший диаметр частиц заданной целевой крупности, другими словами, произвести систематизацию (фракционирование) частиц в заданном размерном диапазоне.

Решение поставленной задачи проводили на базе научного положения о движущейся по заданной траектории частицы с критическим диаметром 5р (рисунок 1). А именно, это положение состоит в том, что в рабочем объёме машины частицы размером, превышающие 5 кр , осаждаются раньше, чем частицы размером не более, чем 5 < 5 кр .

Соответственно, так называемая траектория: ВС – частицы текущим критическим диаметром, А С – частицы глобальным (по Г.И. Бремеру) критическим диаметром (рисунок 1).

Эта (гипотетическая) особенность поведения частицы критическим диаметром в рабочем объёме центрифуги создает предпосылки обосновать математическую модель организации такого режима работы машины, чтобы была обеспечена, в основном, аккумуляция частиц размером 5 е ( 5 1 , 5 2 ) в данном объёме.

В теории седиментации по Г.И. Бремеру под понятием «глобальный критический диаметр» понимают научное положение о том, что при разделении суспензии частицы размером не менее чем 5, полностью уходят в осадок (одновременно с некоторыми частицами меньшим диаметром).

В соответствии с этим при первой обработке исходной суспензии с параметром управления 5 л = 52 и угловой скоростью о может быть записан коэффициент уноса

^ 1 = — = „2² 2 f F O ( ⁵ ( r ) ) rdr, ⁽⁹⁾ n₀ R² - r 2 r' ^v '

где, соответственно, n – число частиц в фугате, ε 1 – относительное число частиц в фугате, то есть в расположенной над линией АС области потока, F о ( 5 ) - счётная функция распределения частиц в исходной суспензии.

Отмеченная особенность процесса осветления данной жидкостной смеси может быть эффективно использована при обосновании аналитического приближённого выражения F 1 ( 5 ) функции распределения на последующем после нулевого этапа обработки порошкообразной субстанции с функцией распределения F 0 ( 5 ).

А именно, в качестве функции распределения используется зависимость

F i ( ⁵ ) =

^F 0 ( ⁵ ) при ⁵ <  ⁵ гл , ^F 0 ( ⁵ гл ) при ⁵ <  ⁵ гл

И так далее, со своим 5 гл , по каждому из этапов расчёта.

Принимая во внимание (7), например, для коэффициента уноса £ 2 (5) в явном виде получают

^ 2 = _R 2^2 J R ^F ( ⁵ ( r ^, ^’ c 0 , ^ ) r^dt ) ,  (11)

где F 1 задано по (10), 5 ( г, о, с о ) - по (5).

Формулы (1)–(11) полагают в основу численного анализа процесса фракционирования порошкообразной субстанции в роторе трубчатой центрифуги, принимая в качестве параметра управления процесса фракционирования частиц на этой машине зависящие от граничных значений 5 гл = 5 1 или 5 2 диапазона целевой фракции (10) угловую скорость ω ротора.

В качестве параметра управления процессом (ПУ) выбирали, последовательно, размеры пробных частиц 5 2 и 5 1 . Эти значения параметров процесса согласно (8) и (9) принимаются в качестве заданных глобальных критических диаметров, сначала 5 _ГЛ2 = 5 ₂, где в соответствии с (5) ^ 2 = V ( c о ) y l ( г ,)/ 5 2 , а затем 5 _Г л1 = 5 .

При этом на базе формул (1), (2) можно сделать заключение о том, соответствующие угловые скорости ротора машины связаны соотношением ^ = ^5/5 •

Образовавшийся осадок с частицами в количестве n 1 = n 0 ε 1 , где ε 1 определяемый по (9) коэффициент уноса, удаляют.

На втором этапе с пробной частицей 5 гл = 5 1 при угловой скорости ω = ω 2 обрабатывают фугат (принимая во внимание, что он уже освобождён от частиц размером больше, чем 5 2 ) имеют целью сохранить в фугате частиц размером, превышающем 5 . Что реализуют на базе коэффициента осветления п = 1 — ^ где Е 2 определяют по (11), П 2 = n 2 / ( n о £ 1 ), n 2 - число отошедших в осадок в фугате частиц размером 5 1 <  5 <  5 2 (вместе с некоторой долей частиц размером меньшим 5 1 ).

По своему смыслу коэффициент осветления П 2 определяет относительное (в долях к количеству ( n ₀ - n 1 ) = n ₀ e i ) число частиц, принадлежащих целевому интервалу 5 е ( 5 1 , 5 2 ).

После чего фугат высушивают, а полученную порошкообразную субстанцию используют как затравочный материал.

Численный эксперимент

Расчеты проводили (в дополнение к данным расчетного примера к формуле (2)) на базе параметров: радиус свободной поверхности жидкости r 0 = 0,015 м; производительность по исходной жидкости Q = 0,2; 0,4 м³/ч; динамической вязкости ц = 0,05 Па - с; начальная концентрация твердой фазы в суспензии с 0 = 1%, 2%.

В качестве счётной функции распределения твердой фазы в исходной суспензии выбирали (8) (по соглашению, рисунок 1), в качестве заданных глобальных критических диаметров частиц заданного целевого диапазона фракционирования 5 1 = 2 • 10^-6 м; 5 2 = 3 - 10 ^-6 м.

Расчёты выполнялись на базе Mathcad 2000 [13].

Грибкова В.А. и др. Вестник ВГУИТ, 2024, Т. 86, №. 2, С. 25-32 Результаты

Визуализация кривых на рисунках 2–5 подтверждает согласие с физическим смыслом исследуемой проблемы. Результаты проведенных аналитических и числовых расчетов процесса фракционирования частиц по этапам проведенного исследования и они имеют убывающий характер.

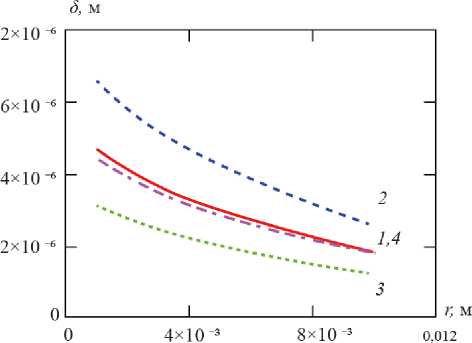
Рисунок 2. Зависимость величины критического диаметра δ пробной частицы от радиальной координаты r при параметрической зависимости диаметра δ от угловой скорости ω и объёмной концентрации с 0 твёрдого (μ = 0,05 Па × с; ω = 1380 с ^-1 : 1 – с 0 = 0,01; 2 – с 0 = 0,02; ω = 2060 с ^-1 : 3 – с 0 = 0,01; 4 – с 0 = 0,02)

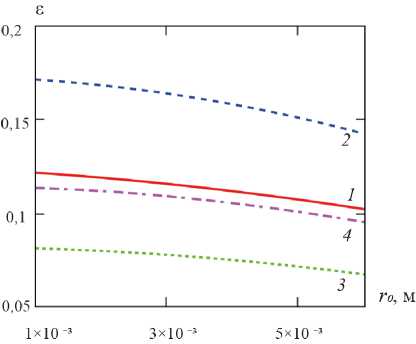
Рисунок 3. Функции счётного распределения частиц, соответственно,   1 – F 0 ( δ ) в исходной суспензии;

2 – F 1 ( δ ) и 3 – F 2 ( δ ) – по первому и второму этапам расчёта по первому и второму этапам расчёта

Figure 3. Countable distribution functions of particles, respectively, 1 – F 0 ( δ ) in the initial suspension; 2 – F 1 ( δ ) and 3 – F 2 ( δ ) – for the first and second stages of calculation

• Figure 2.    Dependence of the critical diameter δ of a test particle on the radial coordinate r with a parametric dependence of the diameter δ on the angular velocity ω and the volume concentration с 0 of solids (μ = 0,05 Па × с; ω = 1380 с ^-1 : 1 – с 0 = 0,01; 2 – с 0 = 0,02; ω = 2060 с ^-1 : 3 – с 0 = 0,01; 4 – с 0 = 0,02)

  

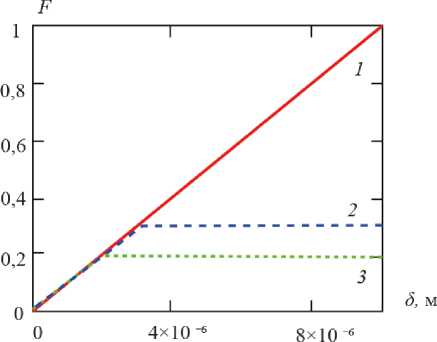
  Рисунок 4. Коэффициенты уноса ε 1 и ε 2 в зависимости от радиуса r 0 свободной поверхности суспензии и параметрической зависимости от угловой скорости ω и объёмной концентрации с 0 твёрдого (μ = 0,05 Па × с; ω = 1380 с ^-1 : 1 – с 0 = 0,01; 2 – с 0 = 0,02; ω = 2060 с ^-1 : 3 – с 0 = 0,01; 4 – с 0 = 0,02)

  Figure 4. Entrainment coefficients ε 1 and ε 2 depending on the radius r 0 of the free surface of the suspension and the parametric dependence on the angular velocity ω and volume concentration c 0 ( μ = 0,05 Па × с; ω = 1380 с ^-1 : 1 – с 0 = 0,01; 2 – с 0 = 0,02; ω = 2060 с ^-1 : 3 – с 0 = 0,01; 4 – с 0 = 0,02 )

  
  
  

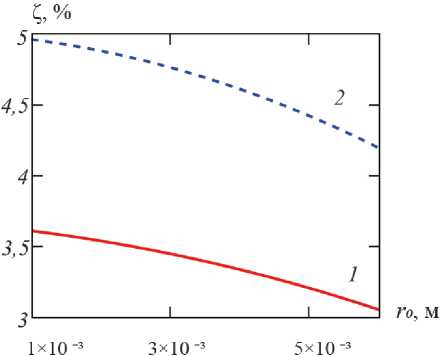
  Рисунок 5. Относительное по исходному составу порошка счётное (%) содержание ζ частиц целевого размерного диапазона при параметрической зависимости от объёмной концентрации с 0 твёрдого ( 1 – с 0 = 0,01; 2 – с 0 = 0,02)

  Figure 5. Relative to the initial composition of the powder, countable (%) content ζ of particles of the target size with a parameter depending on the volumetric mass с 0 of the solid (1 – с 0 = 0.01; 2 – с 0 = 0.02)

  
  

Обсуждение

В рамках постановки задачи, и с учетом данных (рисунки 2, 3, 4), анализ отражённых кривыми этих рисунков, при прочих фиксированных расчетных параметрах процесса показывает, что с увеличением частоты вращения ротора машины содержание частиц, вследствие осаждения их на стенке ротора, всегда снижается (т. е., эффективность работы машины возрастает).

В свою очередь, эффективность процесса обработки затравочного материала, естественным образом, снижается как с увеличением объёмного содержания с твёрдой фазы, так и с ростом производительности машины: например, на рисунке 2 кривая 2 выше кривой 1.

Следует иметь в виду, что предметом исследования является количественный анализ процесса фракционирования исходного затравочного материала заданного объёма по двум последовательным, независимо друг от друга, этапам обработки с коэффициентами уноса ε1 и ε2 по каждому из них. Поэтому расчёт эффективности процесса проводили на базе величины синтетического коэффициента уноса ζ = ε1(1 – ε2), результаты расчёта которого представлены кривыми на рисунке 5.

Заключение

В рамках положений гидродинамики тонкослойного быстровращающегося потока жидкости с взвешенном в нём порошком заданного гранулометрического состава из тонкодисперсных частиц в роторе трубчатой центрифуги впервые предложена методика расчёта для данной машины процедура выделения из порошка совокупности частиц целевого размерного диапазона. Что может быть эффективно использовано для расчёта процесса фракционирования порошка при проектировании инновационных образцов центрифугального оборудования с целью реализации на нём этого процесса.