Расчет прочности нормальных сечений изгибаемых железобетонных элементов с учетом влияния эффекта упрочнения напрягаемой арматурной стали

Результаты экспериментально-теоретических исследований [1] влияния предварительного напряжения арматурной стали на несущую способность изгибаемых элементов свидетельствуют о том, что предварительное напряжение увеличивает не только трещиностойкость и жесткость, как это предписывают действующие нормы, но и существенно увеличивает прочность нормальных сечений за счет выявленного эффекта упрочнения стали.

Так, повышение опытного разрушающего момента М^для балочных образцов с напрягаемой высокопрочной арматурной сталью класса Ат 1200 при уровнях предварительного напряжения o_sp = 0,55; 0,75 и 0,95Од 2^Р по сравнению с обычными образцами (a_sp = 0) в среднем составило 7,4; 14,8 и 17,5% соответственно.

В действующих же нормах строительного проектирования СНиП 52-101-2003, СП 63.13330.2012 и других расчет прочности нормальных сечений преднапряженных изгибаемых элементов производится на основе нелинейной деформационной модели, где в качестве расчетной диаграммы деформирования арматурной стали с условным пределом текучести о₀ , ₂ принимается упрощенная трехлинейная диаграмма (по типу диаграмм Прандтля) без учета упрочнения за площадкой текучести. Предельные напряжения и деформации искусственно ограничиваются соответственно следующими значениями: O_s < 1,1 R_s ; £_s2<  0,015. Таким образом, принятая в нормах расчетная модель не отражает фактическое напряженно-деформированное состояние нормальных сечений, а эффект упрочнения арматурной стали учитывается косвенно, не в явной форме, что в совокупности не способствует достоверной оценке резервов несущей способности рассчитываемых элементов.

В связи с этим разработка корректного расчетного аппарата прочности нормальных сечений предварительно напряженных изгибаемых элементов, учитывающего фактическую диаграмму работы и эффект деформационного упрочнения напрягаемой арматурной стали, представляется весьма актуальной задачей.

Внедрение в расчетный аппарат реальных, в том числе «упрочненных», диаграмм деформирования арматурной стали в координатах " o_s - £_s " позволяет добиваться максимального приближения расчетной модели к физической, тем самым достоверно учитывая фактическое напряженно-деформированное состояние нормальных сечений железобетонных элементов и обеспечивая весомый экономический эффект.

В рамках данной работы предлагается методика расчета прочности нормальных сечений преднапряженных изгибаемых элементов, базирующаяся на диаграммно-энергетическом подходе в теории сопротивления железобетона [2, 3, 4].

На основе обширного экспериментального материала [1], полученного на примере высокопрочной термомеханически упрочненной арматурной стали класса Ат 1200, установлено, что при предварительном напряжении наблюдается существенное повышение характеристик сопротивления a_si ( о₀ , ₀₅ ; 0 0,1 ; о₀₂ и т.д. ) стали малым пластическим деформациям.

Определение параметров a_s [ «упрочненной» в результате преднапряжения диаграммы стали предлагается осуществлять исходя из условия:

Z(E s, _pii + ^.pl + ^£sc + .....)= f ( O s ),                                     ⁽¹⁾

где £^P_pZ - условно-мгновенная пластическая деформация (УМПД) от преднапряжения; £_s , _pZ. - допуск на величину УМПД для искомого параметра o_s.; E_sc - деформации ползучести; ( o_s ) - функция, описывающая исходную диаграмму УМПД.

Важным условием решения задачи в постановке (1) является выбор наиболее корректного способа аналитического описания диаграммы растяжения стали и оценка деформаций ползучести E_sc при длительном действии нагрузки.

Сравнительный анализ различных предложений по аппроксимации диаграммы растяжения стали позволяет заключить, что наиболее достоверным является универсальный метод, основанный на использовании многоинтервальной (сплайн) интерполяции [2, 5]. На примере стали Ат 1200 [1] выявлено, что высокое приближение расчетных кривых "os - £s" к опытным обеспечивается даже при использовании сплайна невысокой степени, а именно кубического сплайна.

В этом случае функция / (os ), аппроксимирующая исходную диаграмму УМПД, представляется как сплайн-функция общего вида:

ⁿ i

/ ( O's ) = S"=imi (-^— ri),

\ CT0,2/ где mz, ri, T^i - безразмерные параметры сплайна; Nt - номер интервала нелинейной части, на котором оценивается параметр £spZ; msf = ^- - относительный уровень загружения стали.

Р       5f0,2

Влияние предварительного напряжения на прочность нормальных сечений изгибаемых элементов, выражающееся в повышении предельных напряжений в арматуре o_sm определяется через коэффициент условий работы m_s ^p :

° sm   ^ms^p ^O0,2 ■

С учетом выражения (3) функция / (os) (2) при использовании кубического сплайна, т.е при ni = п2 = п3 = 3, преобразуется в развернутую систему уравнений (4):

(    ^ms^p 0 0,2

E s m s< _p 0 0,2

—

Osp

;

^£s =

E s m s^p 0 0,2 E s

+ m ! (m_s(p — r i )³

—

Osp

"ES" ;

+ m i (m_sfp — r i )³+ m 2 (m s _fp — Г 2 )³

—

Osp

; ^Es

^mS?P °^0,2 + m i (m s _f p — r i )³+ m 2 (m_s( p — r 2 ) 3 + ^Es

при	0 <  m s^p <	r i
при	r i < m s^p <	r 2
при	r 2 < m s^p <	r 3         (4)
при	r 3 <  msfp <	r 4

+ m 2 (m s _fp —r 2 )³

—

Osp

ЁТ

■

Ввод принятых обозначений m_s ^ _p = x ;

^{9    E}s ^ s

⁺ ° sp ;

Т 1 = m i E_s ;

Т 2 = m 2 E_s ;

Т з = m 3 E s

трансформирует систему уравнений (4) в следующие компактные выражения:

х — 9/0 0,2 = 0 х ³ + п х ² + 6х + с = 0

при 0 < х <  r_i; при r_i< х <  r₄ .

Опуская промежуточные математические выкладки, приведем расчетные формулы для «рабочего» участка работы напрягаемой арматурной стали, соответствующего условию при r 1 < х < r 4 (или o_eZ< O_sm<  o_u с учетом принятых обозначений x = m_s ^ _p и m_s ^ _p = O' sm^/ O o,2 ).

Коэффициенты a, b, с в выражении (7) при r₃< х < r 4 вычисляются по формулам:

а

-

3 (Т 7 1 + Т 2 7)2 + Т з Ч з ) ,

Т 1 + Т 2 +Т 3

;

b =

3 Т Ч² + 3Т 2 Ч 2 ² +3Т з ) з ² + <7о,2 .

с

-

Т 1 + Т 2 +Т 3             ^;

Т 1 7³ + Т 2 Ч³ + Т 3 7 З + _s

.

Т 1 + Т 2 +Т 3

На других участках диаграммы r₂< х < r₃ и Г 1 < х < r₂ коэффициенты а, b, с определяются по формулам (8), принимая соответственно Т₃= 0 и Т₂ = Т₃ = 0.

Используя решение Кардано, подстановкой x = у - п/3, уравнение (7) приводим к «неполному» виду:

у ³ + p у + q = 0,

где

p = - £ + b ; q = 2 ( f ) ³ - 12 + с .

Преобразуем кубическое уравнение (9) в уравнение IV-й степени, приняв следующие обозначения:

£ sm q = ^q 0 - m •

Выражения (9) ^ (11) будут справедливыми и для участков диаграммы т 2 — ^х — Т 3 и Т 1 — х — т₂, если принимать соответственно Т 3 = 0, m 3 = 0 и Т₂ = Т 3 = 0, m₂ = m 3 =0.

Основываясь на гипотезе плоских сечений, по которой £_sm = г ^ _т (। - 1 ) и с учетом условий f = £ j xp_s и £ = ^₀ , ₂ m_s^_p, можно записать:

^E sm          f т _r ^{- E} bm ^.

J V S S 0,2 ^m S^p

Подставляя выражение для E_sm в формулу (11), имеем:

где

q = q₀ + —

1     0     m

—

q i = q o

С учетом примененных замен (5)

_____^bm_____ _       ^А J V s ? 02 m s^p m    ^q1 m s^p ,

।  £bm .      _    £bm m ;         J Vs <0,2 m .

(mt г)! + m₂ )₂ + m₃ ) )

П = - п/3 =    ¹ ---—---3-^ , приходим к выражениям:

m1 + m2+m3

,                                   А ms?P = y + п ;    q = qi - ~~

m_s ^p = x = y - d/3 и вводя очередные обозначения

Подставляя (16) в уравнение (9), получаем искомое уравнение IV-й степени:

у ⁴ + п у ³ + p у ² + (q 1 + р т) У + q 1 т = А.                       (17)

В результате алгоритм определения расчетного разрушающего момента М ^¹ по предлагаемой методике выглядит следующим образом:

• 1.    Определяются коэффициент условий работы m_s ^ _p и действительные напряжения в растянутой арматуре в предельном по прочности состоянии как o_sm = m^ p a₀ , ₂ , в зависимости от участка диаграммы "o_s - e_s ":

• - в интервале т 1 — m_s ^p — т₄ (или Т 1 О 02 — ^CT_sm — ^ и ), соответствующем «рабочей» стадии стали - как решение уравнения IV-й степени (17) методом итерации.

• 2.    По вычисленным напряжениям a_sm из условия равновесия внутренних усилий в сечении определяются высота сжатой зоны бетона х и расчетный разрушающий момент М ^¹ :

• ^R b Л ь ^- S ^ si. A si = ^{0 ;} М ^ = R b S b + So st S i .

Высокая точность рекомендуемой методики расчета прочности нормальных сечений с учетом эффекта механического упрочнения арматурной стали в процессе предварительного напряжения подтверждается экспериментальными данными, полученными в результате испытания опытных изгибаемых преднапряженных элементов балочного типа с высокопрочной арматурной сталью Ат 1200 [1]. Средняя величина расхождения опытного М¹^ и расчетного М ^ значений разрушающего момента составила А М_и « 4,5% (при максимальном значении А М max = 5,4%).

Следует признать, что расчеты по предлагаемой методике объективно сопряжены с определенными сложностью и трудоемкостью вычислительных процедур, так как диаграмма УМПД стали аппроксимируется многоинтервальной сплайн-функцией вида (2) и (4), а параметры o_s i «упрочненной» в результате преднапряжения диаграммы осуществляются исходя из многофакторного условия (1). Принимая во внимание данное обстоятельство, в рамках данного раздела авторы разработали программу «машинного» счета с применением ЭВМ, написанную на языке программирования Фортран. Структура, блок-схема программы приводятся на рисунках 1 и 2. С использованием данной программы все сложности, связанные с математической обработкой числовых данных, утрачивают свое влияние.

Структура программы

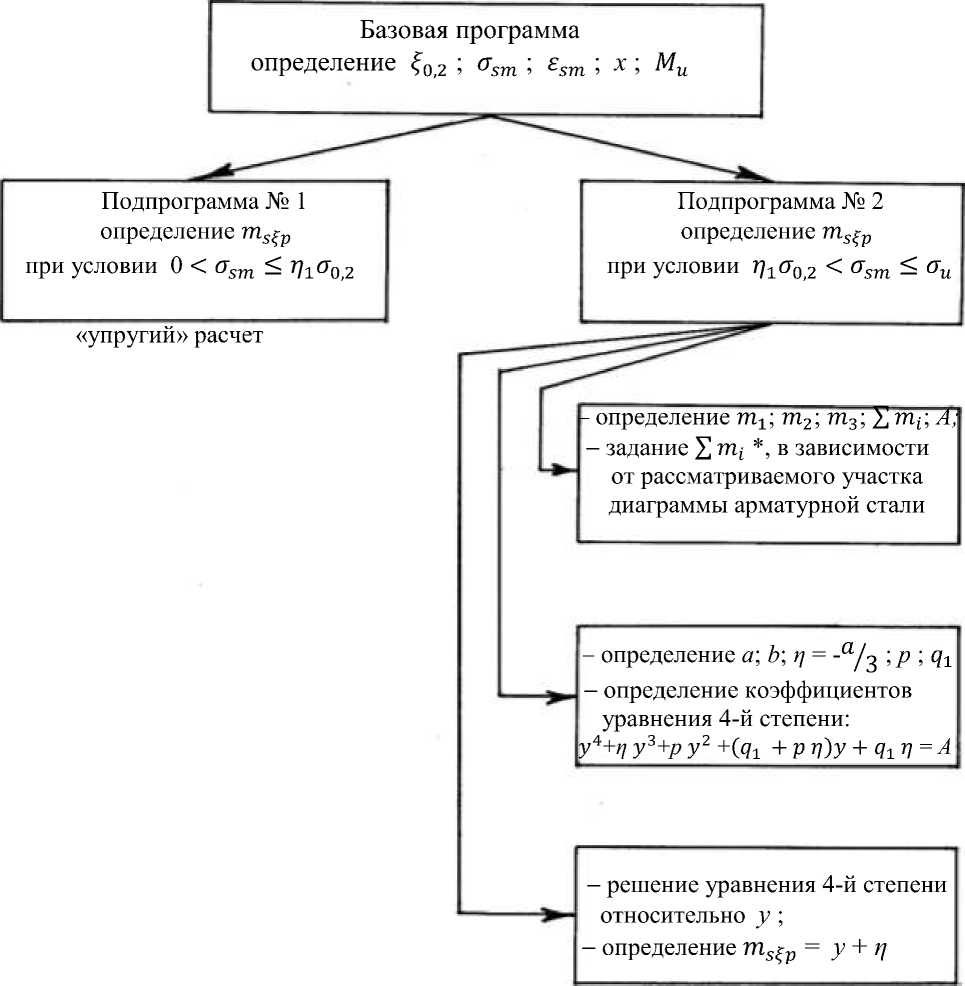
* Примечание:

- участок №1;	0 <  ^ sm — ^1с0 , 2 ( расчет по подпрограмме № 1);
- участок №2;	^ 1 ^ 0,2 <  ° sm — ° 0,2    ( т 1 * 0; т 2 = т з = 0);
- участок №3;	^ 0,2 <  ° sm — ° 0,5    ( т1 ^ 0; т2 ^0; т3 = 0);
- участок №4;	^ 0,5 <  CT sm — ° Н     ( т 1 * 0; т 2 ^0; т з *0).

Рисунок 1 – Структура вычислительной программы «Расчет прочности нормальных сечений железобетонных изгибаемых элементов с учетом влияния эффекта упрочнения напрягаемой арматурной стали» (диаграмма арматурной стали аппроксимирована по четырем участкам кубическим сплайном)

ввод исходных данных №1

Сокращенная блок-схема программы

Базовая программа определение R _b • b ; j ; o _sc • A'_sp ;

R sc ^A S ; ^ 0,2

Базовая программа определение R _b • b ; j ; a _sc • A'_sp ;

R sc ^A S ; ^ 0,2

расчет при ожидаемом

0 <  O sm < 1 1 ^ 0,2

(подпрограмма №1)

переход (возвращение) на базовую п р о г р а м му

0 <  O _Sm <  Л 1С Г 0,2

да

ввод исходных данных №2

нет

- определение m 1 ; m 2 ; т₃

- определение s _sm (базовая программа)

Расчет при tv^ <  Osm < 0 0,2 (Е m _t = m ₁ ; m 2 = m₃ = 0);

^msi;p ; ^Osm

ввод исходных данных №3

Л 1 ° 02 <  ^Osm < O

да

__□

- определение x ; M_u (базовая программа)

нет

Расчет при 0 0,2 <  O sm < 0 0,5 (Lm _t = m 1 + m 2 ; m ₃ = 0); определение m _s^_p и o _sm

stop

да

^ 0,2 < O sm < 0 0,5

нет

Расчет при 0 0,5 <  O sm <  o _u (Е m _t = m 1 + m 2 + m₃); определение m _s^_p и a _sm

да

У о,5 <  O m < O

Рисунок 2 – Сокращенная блок-схема вычислительной программы «Расчет прочности нормальных сечений железобетонных изгибаемых элементов с учетом влияния эффекта упрочнения напрягаемой арматурной стали» (диаграмма арматурной стали аппроксимирована по четырем участкам кубическим сплайном)

Выводы

• 1.    Среди комплекса факторов, определяющих влияние преднапряжения a_sp на прочность изгибаемых элементов по нормальным сечениям, главенствующими являются усилие обжатия и выбираемые при натяжении пластические деформации арматурной стали, которые обусловливают изменение ее механических свойств (в первую очередь повышение условного предела текучести Oq,₂ ) и трансформацию диаграммы растяжения.

• 2.    Разработана методика расчетной оценки повышения прочности нормальных сечений изгибаемых элементов на основе диаграммного подхода. Высокая точность рекомендуемой методики обусловлена более достоверной оценкой предельных напряжений в арматурной стали o_sm с учетом эффекта ее упрочнения при преднапряжении . Наилучшее приближение расчетных и опытных значений, характеризующих прочность нормальных сечений, наблюдается при использовании расчетной диаграммы стали, аппроксимированной по четырем участкам методом многоинтервальной сплайн-интерполяции.