Расчет профиля скоростей и температур расплава в кольцевом канале экспандера

В литературе достаточно полно и детально освещены процессы течения расплавов в каналах различной формы: в круглом, щелевом, кольцевом и др. каналах [1]. Однако в приводимых автором решениях не учтены особенности течения расплава в экспандере, так как в нем обработка проводится при более высокой влажности (до 26 %), за счет ввода пара, и более низких температурах (от 80 до 130 ºС) и давлении (до 40 МПа) в течение очень кор откого периода (не более 6 секунд).

Выпрессовывание продукта в экспандере происходит через регулируемый кольцевой зазор, а не через матрицу с фильерами, как в экструдере [2].

В связи с тем, что обработка смеси зерновых и зернобобовых культур в экспандере проводится при более высокой влажности, а разогрев продукта осуществляется не только за счет трения (эффекта диссипации), но и за счет ввода пара, то для разработки и создания формующей головки экспандера необходимо оп -ределить ее форму и размеры, которые обеспечивали бы стабильную работу экспандера.

Рис. 1. Канал экспандера с кольцевым сечением

Для описания неизотермического течения расплава в кольцевом канале экспандера (рис. 1) используем следующие уравнения [1]:

• -    уравнение неразрывности, описывающее изменение плотности расплава в зависимости от времени как функция вектора потока массы p v,

др    др    др    др

--+ vx + v_y + v — д t д x ^у ду д z

= - Р

( Pv_х^{д v} y д v )

x_ +       . z_ v дx   ду   дz у

- уравнения движения:

d v x	_ др —--	' дт хх	+	дТ,х yx	дт^ . zx	)	+ p g x
dt	д x	^ д x		д у	д z	у
d v у	_ др —--	( дт xy	+	дт уу	+<т	^	+ р ду , (2)
dt	д у	( д x		д у	д z
dv z	_ др —--	<дт xz	+	дT yz	дтИ + — zz	^	+ p g z
dt	д z	vдX		д у	д z	у

- реологическое уравнение течения расплава

Т = у / ф .

Если в процессе неизотермического течения наблюдается теплопередача, то для описания такого процесса необходимо включить следующие уравнения [1, 4]:

• -    уравнения термодинамического состояния расплава (уравнение теплопроводности Фурье):

  aq , 8 T — = —л . д у д у

  
  
  
  

  - закон сохранения энергии:

  
  

  д д t

  
  

  p U + 2 pv¹

  
  

  —

  
  

  д I     т '       2 |     д [              1       2 |     д      [              1 2

  —v_T p U + — p v +-- v„ p U + — p v + v, p U + — p v

  8x x (       2     )   8у y (       2     )   8z ^z (       2

  
  

  ^д q x ₊ ^д q y ₊ ^д q_z д x 8y   8z

  
  

  i д .a д

  ⁺ p ( v x g x ⁺ v y g y ⁺ v z g z M д Х Pv x +д у Pv y +д ^ Pv:

  
  

  _—

  
  

  Tv_x + T _vv _v + T v, + t _xv_x + t _v v_v ax a xx x xy^y xz z)   gу \ yx x yy y

  
  

  + Tv_z +~ C t vx + t v + t v_z ) + ф yz z / д \ zx x zy у zz z /

  
  

  , (5)

  
  

  Система уравнений (1-5) не может быть решена в общем виде. Поэтому для расчета полей скоростей и температур в регулируемом кольцевом зазоре экспандера были приняты следующие допущения: течение расплава в кольцевом зазоре экспандера представляет собой установившийся ламинарный поток; силами инерции и гравитации можно пренебречь по сравнению с силами трения и давления; скольжение расплава на стенке отсутствует; течение изотермическое , т. е. все частицы расплава имеют одинаковую температуру; расплав представляет собой несжимаемую жидкость, характеризующуюся постоянными теплопроводностью и температуропроводностью; конвективная теплопередача в направлении течения выше, чем теплопередача за счет теплопроводности, т. е. изменением теплопроводности в продольном направлении можно пренебречь; теплопередача в направлении, перпендикулярном направлению течения, происходит только за счет теплопроводности.

  Для решения системы уравнений (1-5) были приняты следующие граничные условия по температуре: при прилипании расплава к стенкам канала тепловой поток в слое, прилегающем к стенке, определяется следующей формулой:

  —) = _Bi ^т к ^{— т} т . (₆) ( ay J а

  ст

  Оно относится только к тепловому потоку в направлении, перпендикулярном поверхности контакта между стенкой канала и расплавом.

  Уравнения (1-6) совместно с начальными условиям v x 0 = v x ( ху т = 0 ) , v y 0 = v y ( x.y j = 0 ) , T ₀ = T ( x,y, T = 0 ) и соответствующими граничными условиями представляют замкнутую сис

  
  

  тему, позволяющую определять поля скорости и температуры однородной несжимаемой вязкой жидкости и их изменение со временем.

  Температура расплава, контактирующего со стенкой, принимается равной температуре стенки, то есть T к = T с _т . Это условие считается условием изотермичности стенки (Bi ^да ).

  Для решения системы уравнений (1-6) был использован численный метод конечных разностей, при использовании которого канал головки экспандера разбивался на расчетные ячейки с помощью сетки [3]. Сетка состояла из прямоугольных ячеек с постоянным шагом между узлами, которые точно лежат на границах области интегрирования. При этом дифференциальные уравнения преобразовывались в разностные уравнения путем замены производных в точке конечными разностями по границам ячейки [3, 4].

  В результате были получены уравнения для определения текущей v_z и средней скоро

  
  

  сти v z расплавав кольцевомканале экспандера:

  
  

  v_z

  
  

  v z

  
  

  A pR ² 4 p L

  

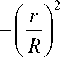
  + ( k ² — 1)ln[( r / R ) — k ]

  
  

  A pR R 8 n L

  
  

  1 + k ² +

  
  

  1 — k ² " ln k ,

  
  
  
  
  
  

  где ^k = R min / R max .

  Объемный расход V получают, умножая выражение для средней скорости на площадь поперечного сечения кольцевого зазора:

  
  

  "A PR⁴ у, Иа^(1 — k ²)²

  --------- (1 — k ) +--

  8 n L             ln k

  
  
  
  

  Было также получено решение для расчета профиля температуры расплава в кольцевом канале экспандера:

  
  

  / X m + 1

T (z■) = T + ф f* ) x ст

Л V dz )

( П П \ ^m + 3 m + + 3 "O^) _x ( R max - R min )   - y

2 ( m ² + 5 m + б )

Полученное решение для профиля температуры справедливо при условии, что пол- ная энергия, рассеиваемая при течении, отводится за счет теплопереноса в направлении, перпендикулярном направлению течения, т. е. через стенки кольцевого канала экспандера.

На рис. 2 представлены расчетные скорости и температуры расплава в кольцевом канале экспандера при постоянной температуре стенки рабочей камеры Т ст = 398 К и различной длине канала, мм: 1 – 1700; 2 – 1900; 3 – 2100.

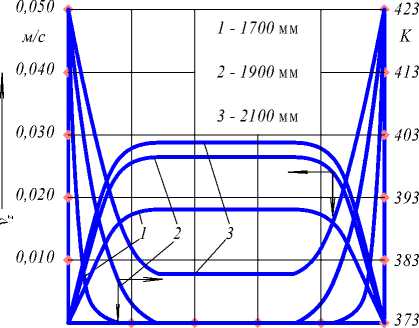
0       0,2      0,4      0,6      0,8      1,0

r/R

Рис. 2. Профили скорости и температуры расплава в кольцевом канале экспандера при постоянной температуре стенке Т ст = 398 К и различной длине канала, мм: 1 – 1700; 2 – 1900; 3 – 2100.

Полученные зависимости достаточно адекватно описывают профиль скоростей и температур расплава в кольцевом канале экспандера и могут быть использованы в методике инженерного расчета экспандера [4].

Условные обозначения g – вектор ускорения свободного падения; vx, vy и vz – компоненты вектора скорости; v2 = vX + v2 + v2; < - вектор потока теплоты (с компонентами qx, qy, qz); Bi – число Био; Tcт – температура расплава на стенке, К; Tк – температура корпуса кольцевой головки экспандера, К; vz – скорость расплава вдоль оси z, м/с; vz – средняя скорость в кольцевом канале экспандера, м/с; ρ – плотность расплава, кг/м3;

х, у, z - координатные оси, п = 1/ф — коэффициент динамической вязкости, Па - с; ф - показатель консистенции (текучесть); p – давление, Па; d p / д z - градиент давления, Па; m - индекс течения; L – длина выходной зоны, м; Н – глубина винтового канала, м; λ – коэффициент теплопроводности, Вт/(м - К); 5 - толщина зазора, м; t - время, с; т - напряжение сдвига, Па - с; Ф – диссипационный член; q – удельный тепловой поток, Вт/(м² - К); r , R - текущий радиус и радиус кольцевого канала, м; U – внутренняя энергия, Дж; V – объемный расход, м³/с; Y - скорость сдвига, с^-1.