Расчет работоспособности трибосопряжения «поршневой палец - верхняя головка шатуна» тракторного дизеля

Введение. Условия работы шатунной группы характеризуются интенсивными знакопеременными нагрузками от газовых и инерционных сил и повышенными температурами рабочей среды. Плавающий поршневой палец в соединении с поршневой головкой шатуна образует сложнонагруженный подшипник скольжения с ограниченным поступлением смазочного материала. Через поршневой палец передаются все силы, возникающие между поршнем и шатуном. Работающее под большой механической и термической нагрузкой трибосопряжение обеспечивается смазкой через отверстие в головке шатуна и бронзовой втулке. Масло в это отверстие поступает из внутренней полости поршня, куда оно вбрызгивается масляной форсункой или поступает через отверстия в поршне от маслосъемных колец.

Условием долговременной работы сложнонагруженного подшипника является наличие в достаточном количестве смазочного материала, обеспечивающего получение преимущественно жидкостного режима трения. В этом случае потери на трение в подшипнике достаточно малы, а износ деталей минимален.

Таким образом, установление условий существования смазочного слоя, его величина, а также определение значения воспринимаемой этим слоем нагрузки является определяющим условием работы и несущей способности подшипника.

Основные уравнения. Поведение слоя смазки, заключенного между поверхностями трения, описывается системой уравнений гидродинамической теории смазки, теплопередачи, а поверхности трения считаются границами смазочного слоя, которые обладают в реальности упругопластическими свойствами. Конструкцию сложнонагруженного подшипника оценивают сравнением параметров расчетной траектории, по которой под действием приложенных нагрузок движется центр шипа, и набором взаимосвязанных гидромеханических характеристик [1].

Исходными уравнениями для расчета гидромеханических характеристик шатунных под- шипников являются: уравнение для поля гидродинамических давлений в смазочном слое, разде- ляющем произвольно нагруженные поверхности; система уравнений плоского движения центра

шатунной шейки; уравнение теплового баланса [1].

X ′

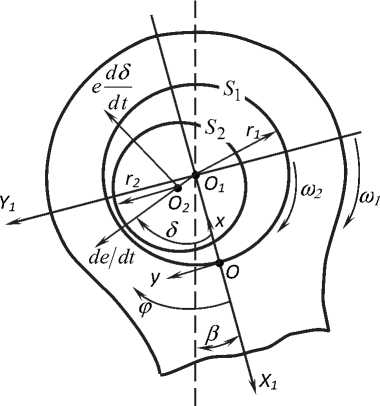
Рис. 1. Схема радиальной опоры

Геометрию смазочного слоя (рис. 1) рассматриваем в системе координат с полярным углом ϕ и полярной осью О ₁ X ₁, жестко связанной с подшипником (шатуном) и вращающейся вместе с ним с угловой скоростью ω 1 . Оси Ox , Oz системы координат Oxyz , в которой рассматриваются процессы в смазочном слое, лежат в плоскости, на которую развертывается поверхность отсчета S 1 , ось Oy направлена по нормали к ней, - B 2 ≤ z ≤ B 2, где B – ширина опоры.

В системе координат Oxyz подшипник неподвижен, шип вращается с угловой скоростью ω21 =(ω2 -ω1). На шип в плоскости Oxy в сечении z = 0 действует переменная по времени t внешняя сила F (t). Центр шипа O2 движется в плоскости Oxy с относительной скоростью, проекции которой на линию центров и направление ей перпендикулярное равны e′ = dedt и eδ′ =edδdt, где e(t)= O1O2 – смещения центров масс шипа относительно подшипника, δ(t) – угол положения линии центров.

Для определения поля гидродинамических давлений p ( ϕ , z ) в тонком смазочном слое (рис. 1) достаточно широко используется обобщенное уравнение Рейнольдса, в обозначениях работы [2] записываемое в виде:

1 д h ³ d p _д_ h ³ d p r ² дф 12 ц дф d z 12 ц д z

ω 21 ∂ h  ∂ h  ∂ h

++ .

2 ∂ϕ  ∂ z ∂ t

При интегрировании уравнения (1) в области Ω= ( ϕ ∈ 0,2 π ; z ∈ - B /2, B /2 ) чаще всего применяют граничные условия Свифта – Штибера, которые записывают в виде следующих ограничений на функцию p ( ϕ , z ) :

p ( ϕ , z =± B /2 ) = p_a ; p ( ϕ , z ) = p ( ϕ+ 2 π , z ); p ( ϕ , z ) ≥ p_a .                                      (2)

При наличии на поверхностях трения шипа и подшипника источников для подачи смазочного материала в слой условия (2) должны быть дополнены соотношением

p ( ϕ , z ) = p _S при ( ϕ , z ) ∈ Ω _S , S = 1,2,..., S ^* ,                                                     (3)

где Ω _S – область источника смазки, где давление равно давлению подачи p _S , S * – количество источников.

Для определения угловой скорости шипа относительно подшипника ω 21 определяем угловую скорость шатуна.

Как известно, λ⋅ sin ( α ) β = arctg                 ,

1 - λ ² sin ² ( α )

R где λ= k . Здесь R – радиус кривошипа, L – длина шатуна.

L ш

Следовательно, to =р =

X- cos ( a ) 1 -X ² sin ² ( a )

to ,                                                                       (4)

где to y - угловая скорость вращения коленчатого вала.

Так как поршневой палец считается неподвижным, т. е. to2 = 0, относительную угловую скорость определим как to21 = (to2-to1 ) = -to1.

Толщина смазочного слоя с учетом произвольной геометрии поверхностей трения шипа и подшипника без перекоса их осей определяется выражением:

h ( ф , z , t ) = h * ( ф , z , t ) - e ( t ) 008( ф-б ( t ) ) ,                                                                (5)

где h * ( ф , z , t ) - толщина смазочного слоя при центральном положении шипа в подшипнике с неидеальной геометрией.

Величины e ( t ) , 5 ( t ) определяются решением системы уравнений движения. Методика расчета динамики и гидромеханических характеристик шатунного подшипника рассмотрена в [1, 3].

При определении поля гидродинамических давлений обычно учитывают зависимость вязкости смазки от температуры и давления [3]. Вязкость рассчитывается как функция некоторой эффективной за цикл нагружения температуры Т _э , значение которой определяется из уравнения теплового баланса, отражающего равенство за цикл t _ц количеств теплоты, рассеиваемой в смазочном слое и отводимой смазкой, вытекающей в торцы подшипника.

Для решения уравнения (1) с учетом соотношений (2), (3), (4) используют численные методы, среди которых наибольшее распространение получили вариационно-разностные методы с использованием конечно-элементных аппроксимирующих моделей и методы конечных разностей. Использование методов, основанных на конечно-разностной аппроксимации дифференциальных операторов краевой задачи со свободными границами, позволяет наиболее просто и быстро получать решения достаточной точности для подшипников с неидеальной геометрией слоя, учесть наличие источников смазки на поверхности трения. Одним из эффективных приемов интегрирования уравнения Рейнольдса при помощи методов конечных разностей является использование многосеточных алгоритмов, что позволяет на порядок уменьшить затраты времени на решение. Уравнение (1) после его аппроксимации сводили к системам алгебраических уравнений, которые с учетом соответствующих граничных условий решали итерационным методом Зейделя.

Разработка критериев оценки работоспособности сложнонагруженных гидродинамических подшипников поршневых и роторных машин является неотъемлемой частью современных методов расчета и проектирования. В то же время достоверность самих методов во многом зависит от применяемых критериев. Достоверность критериев оценивается, как правило, на основе сопоставления расчетных результатов с данными, полученными экспериментально или в процессе эксплуатации. На основе экспериментальных исследований и современных методов расчета разработаны критерии работоспособности гидродинамических трибосопряжений: наименьшая допустимая толщина смазочного слоя h доп , наибольшее допустимое гидродинамическое давление p доп , приведенная к диаметру шейки минимальная толщина смазочного слоя h pr , максимальная удельная нагрузка f _max .

Оценка работоспособности подшипников также проводится по расчетным величинам относительных суммарных за цикл нагружения протяженности областей a _h и a p , где значения наименьших за цикл нагружения значений толщины смазочного слоя inf h _min меньше, а значения наибольших гидродинамических давлений в смазочном слое sup p max больше допустимых величин. Опыт свидетельствует, что значения этих параметров не должны превышать 15–20 %.

Если значения толщины смазочного слоя h _min достигают критических значений h _доп или становятся меньше последних, будем считать, что гидродинамический режим трения переходит в граничный.

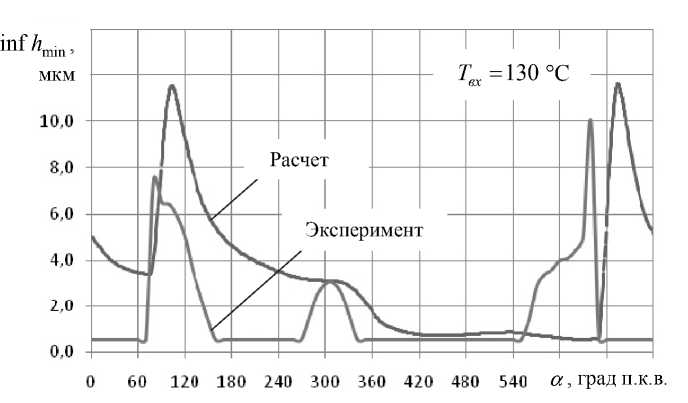
Результаты расчета. Исследования проводились на примере расчета динамики поршневого пальца двигателя 4ВН 15/16. В качестве основных гидромеханических характеристик, помимо inf h min , sup p max , α _h доп и α _p доп , были рассмотрены среднеинтегральные значения: приращения температуры смазки Δ T ; потерь мощности на трение N ^* ; расходов смазки Q ^* . Расчеты выполняли на двух режимах работы двигателя (режим максимальной мощности N _max и режим максимального крутящего момента M _max ), ширина подшипника B = 52 мм, диаметр D = 60 мм, диаметральный зазор Δ= 30 мкм, давление подачи p вх = 0,4 МПа, угловая скорость вращения коленчатого вала ω _v = 177,9 с –1 и ω _v = 130,8 с –1 для соответствующих режимов работы. Температура подачи смазки T _вх варьировалась от 110 до 130 °С и от 80 до 110 °С соответственно для режимов N _max и M _max . В качестве h _доп принимали 1,9 мкм.

Результаты расчета представлены в табл. 1, 2 и на рис. 2–4. На рис. 2 и 3 представлено сравнение расчетных и экспериментальных данных, полученных для исследуемого подшипника по методике, описанной в статье [4]. Некоторые расхождения экспериментальных и расчетных результатов объясняются тем, что в представленных расчетах не были учтены тепловые деформации поршневой головки шатуна. Из рисунков и таблиц следует, что минимальная толщина смазочного слоя во многих случаях меньше допустимого значения и продолжительность его существования α _h доп превышает 20 % от цикла нагружения, что свидетельствует о переходе жидкостного режима трения в граничный режим.

Таблица 1

Гидромеханические характеристики подшипника на режиме максимальной мощности ^max

T , °С вх	Δ T , °С	N * , Вт	Q * , л/с	sup p max , МПа	inf h min , мкм	α , % доп
110	3,4	10,75	1,9 ⋅ 10 - 3	153,0	1,05	38,3
113	3,1	10,35	2,05 ⋅ 10 - 3	158,6	0,96	38,9
120	2,4	9,46	2,45 ⋅ 10 - 3	162,8	0,77	39,8
125	1,9	8,97	2,82 ⋅ 10 - 3	170,4	0,65	40,8
130	1,6	8,42	3,26 ⋅ 10 - 3	175,9	0,53	41,2

Таблица 2

Гидромеханические характеристики подшипника на режиме максимального крутящего момента ^max

T , °С вх	Δ T , °С	N * , Вт	Q * , л/с	sup p max , МПа	inf h min , мкм	α , % доп
80	7,4	9,77	0,80 ⋅ 10 - 3	150,6	1,97	0
85	6,2	9,11	0,89 ⋅ 10 - 3	152,9	1,78	8
90	5,2	8,48	0,99 ⋅ 10 - 3	154,8	1,59	31
100	3,6	7,32	1,24 ⋅ 10 - 3	165,9	1,25	36
110	2,4	6,35	1,59 ⋅ 10 - 3	173,7	0,95	38

Увеличение температуры подачи смазки ведет, как и следовало ожидать, к снижению толщины смазочного слоя. Однако для более детального определения влияния температуры необходимо учитывать не только значение T _вх , но и распределение температуры в окружном и радиальном направлении, а также изменение геометрии смазочного слоя вследствие упругой деформации верхней головки шатуна.

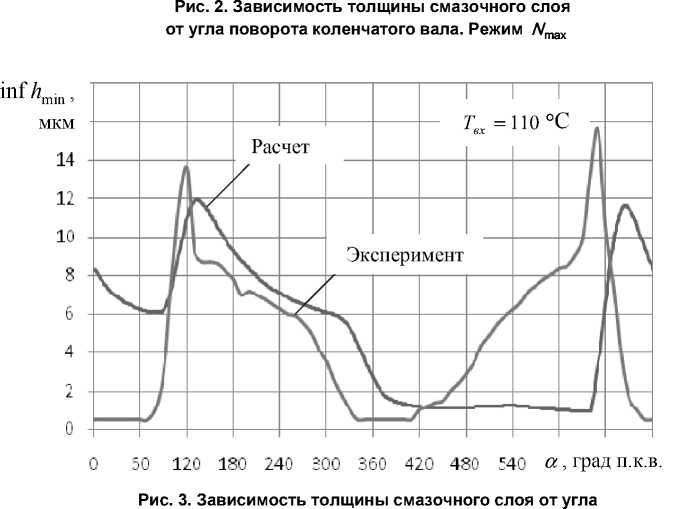
поворота коленчатого вала. Режим ^max

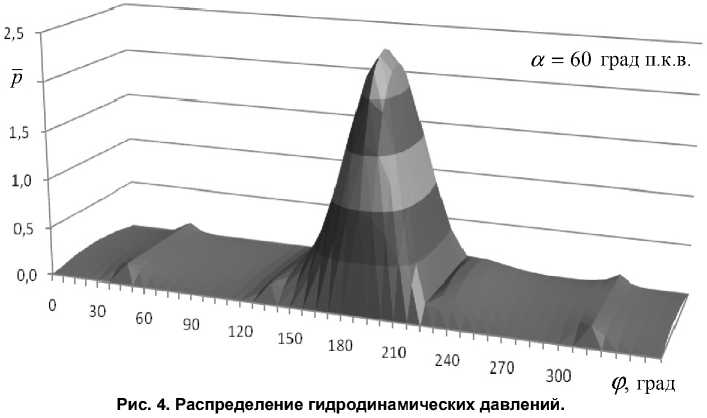
Режим ^max

На рис. 4 представлена эпюра гидродинамических давлений в тонком смазочном слое подшипника для положения а = 60 град. п.к.в.

Для расчета трибосопряжения в режиме граничного трения необходимо учитывать наличие высоковязких граничных слоев, адсорбированных на поверхностях трения. Влияние этих слоев сказывается именно при сближении поверхностей трения до величин, сравнимых с высотой микронеровностей [5].

Представленная работа выполнена при поддержке Федеральной целевой программы «Научные и научно-педагогические кадры инновационной России на 2009–2013 годы» и Российского фонда фундаментальных исследований (проект 10-08-00424).