Расчеты сжатия сферической слоистой системы ударными волнами с учетом переноса тепла излучением в различных приближениях

Одним из направлений исследования процессов имплозии (взрыва, направленного не наружу, как обычно, а внутрь) на лазерных установках является математическое моделирование режимов с обострением, то есть таких, которые допускают существование неограниченных решений за конечный промежуток времени. Ранее такие задачи рассматривались в работе [1] для изучения поведения экстремальных решений. К ним относятся безударное сжатие в газовой динамике, задачи теплового взрыва, процессы кумуляции ударных волн и другие [2, 3] . Моделирование совместной с газодинамикой системы переноса тепла излучением может существенно влиять на решения таких задач, в частности, сделать неограниченные решения ограниченными, но с дельтаобразным поведением основных величин. Поэтому возникает интерес к процессам, близким к режимам с обострением, но с одновременным учетом лучистого переноса и газодинамики.

Задача о сходящейся сферической ударной волне впервые решена немецким ученым Г. Гудерлеем, в 1942 году [4] и, независимо от него, Л.Д. Ландау и К.П. Станюковичем в 1944 году [5] . В общей форме описание движения сферической ударной волны есть в книгах [6, 7] . В момент прихода ударной волны в центр происходит ее фокусировка в центре и отражение от него. Вблизи точки фокусировки сходящейся волны растут температурные градиенты, поэтому при учете теплопереноса теплопроводность и излучение становятся основными механизмами диссипации энергии. Задача о сходящейся сферической ударной волне с учетом лучистой теплопроводности решена Е.И. Забабахиным и В.А. Симоненко [8] , которые показали, что теплопроводность видоизменяет характер процесса: вместо конечной плотности и бесконечной температуры возникает бесконечная плотность и конечная температура. За счет теплопроводности перед фронтом ударной волны появляется зона, называемая тепловым предвестником, в которой газ не только нагревается, но и начинает двигаться и уплотняться.

Кумулятивный эффект можно получить и другими способами. В работе [9] продемонстрировано, что в слоистой системе из чередующихся легких и тяжелых плоских слоев плотность и давление могут возрастать. Описать движение ударной волны в слоистой системе намного сложнее, чем в однородной среде, поэтому моделирование таких систем производится, в основном, численными методами. Соответственно, в сферической геометрии степень кумуляции значительно выше, чем в плоской, поскольку ударная волна усиливается за счет суммирования

Статья опубликована в открытом доступе по лицензии CC BY 4.0

двух факторов: сферичности и слоистости. В работе [10] предложена тестовая задача сжатия простейшей сферической системы, состоящей из двух веществ, с учетом переноса излучения в разных приближениях. Показано, что при сжатии ударными волнами особенностью задачи является резкое увеличение плотности вещества в центре сферы. При этом максимальная плотность достигается после прохождения третьей ударной волны. Такие режимы, когда средние плотности веществ становятся больше в десятки раз, по-видимому, также можно отнести к задачам с обострением. До выхода на стационарный режим основные газодинамические величины в данной задаче (температура, плотность, давление и скорости границ веществ) представляют собой осциллирующие функции. Возникающие под воздействием сильных ударных волн осцилляции всех величин очень резки и для их качественного воспроизведения требуются прецизионные методы. Достоинство предложенной задачи заключается в том, что все анализируемые в ее постановке приближения лучистого переноса дают близкие результаты для основных термодинамических величин, а при выходе на стационарный режим их точные значения одинаковы для всех приближений.

Ранее в работе [11] для тестирования многомерных программ, описывающих процессы радиационной газовой динамики, рассмотрены задачи сжатия ударными волнами сферической слоистой системы, состоящей из нескольких веществ, при совместном учете лучистой теплопроводности и газодинамики. Особенность этих задач — достижение максимальной плотности после прохождения второй или третьей ударной волны. В статье [12] одна из этих задач с небольшими изменениями моделировалась в кинетической постановке. Изучалось поведение конечно-разностных схем для кинетического уравнения переноса. В данной работе для решения этой же задачи дополнительно применяется шесть упрощенных моделей лучистого переноса.

• 2.    Система уравнений высокотемпературной газовой динамики

При математическом моделировании система уравнений высокотемпературной газовой динамики [13] расщепляется по физическим процессам и на каждом шаге по времени решается в два этапа. На первом этапе рассчитываются уравнения газовой динамики — законы сохранения массы, импульса, энергии газа (газодинамическое движение представляется в эйлерово–лагранжевой системе координат по методике [14] ):

d!+p Vu=0, pdu+^P=0, dt p—.- +P V'U = 0.

dt

Здесь: t — время; ρ — плотность вещества; u — вектор газодинамической скорости; ∇ — векторный дифференциальный оператор; P = p + p r — полное давление, при этом p ( p,T ) — его газодинамическая составляющая и p r = oT /3 — давление излучения; T ( r ,t ) — температура вещества; г — радиус-вектор произвольной точки системы; T _r = 4]RId Q / ( Aa) — радиационная температура; I ( r , Q ,t) — интенсивность излучения; Ω — единичный вектор направления полета фотонов; σ — постоянная Стефана–Больцмана; c — скорость света; E(p,T ) — удельная внутренняя энергия. На втором этапе на основе кинетической модели рассчитывается изменение внутренней энергии за счет лучистого теплообмена в различных приближениях. Кинетическая модель имеет вид [12] :

ρd c dt

( I} + QV +(ac + as)I = ac B + Os U, \ p J                    4n    4n pddE=ac(U-B)

Здесь: a _c ( p,T ) — коэффициент поглощения, [см ^{- 1} ]; a _s ( p,T ) — коэффициент рассеяния, [см ^{- 1} ]; B ( T ) = AaT ⁴ ; U ( r ,t ) = j'dd Qi — плотность энергии излучения, умноженная на скорость света с.

Систему уравнений переноса тепла излучением дополним начальными и граничными условиями:

I (r,Q,t = 0)= 10(r,Q), I (r e r,n Q < 0,t) = I - (r e r,Q,t), T (r,t = 0)= T 0(r), где n — внешняя нормаль к границе Γ расчетной области Γ .

Обозначим через S ( r ,t) = f O ld O вектор потока энергии излучения. Проинтегрировав уравнение переноса по О с весами 1, О , получим систему уравнений:

ρd c dt

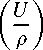
+ V^ S +a c U = a c B,

ρβ d S c dt ρ

+V(DU) + (ac+as)S = 0, где D = {Dij } — симметричный тензор квазидиффузионных коэффициентов и в — параметр, определяющий вид приближения, с которым рассматривается лучистый теплообмен:

в =1, D ij = U - 1

ΩiΩjIdΩ — гиперболическое квазидиффузионное (КД) [15], в = 0, Dij = U-

1 ΩiΩjIdΩ — параболическое квазидиффузионное (ПКД) [16], в =1, Dij = Sj/3 — P1[17], в =1/3, Dij = 6j/3 — P1/3[18], в = 0, Dij = Sij /3 — диффузионное (ДФ) [19],

S ij — символ Кронекера (i,j = 1 7 n, n — размерность пространства R ⁿ ).

Соответствующие начальные и граничные условия имеют вид:

U ( r ,t = 0) = U ⁰ ( r ), S ( r ,t = 0) = S 0( r ), T ( r ,t = 0)= T ⁰ ( r ), aU - в( п - S )= 7.

Здесь a, в , Y — параметры граничных условий, причем a > 0, в ^ 0, a+в > 0.

При численном моделировании кинетического уравнения переноса для уменьшения числа переменных, времени счета и объема занимаемой памяти ЭВМ применяются различные предположения [13] , позволяющие свести задачу к более простой. Например, если допустить линейную зависимость интенсивности излучения от направления полета частиц, то найдем Р1 приближение метода сферических гармоник. Далее, ожидая, что между плотностью и потоком излучения существует зависимость в виде закона Фика, получим диффузионное приближение. Считая, что справедливо приближенное равенство U = B (условие локального термодинамического равновесия), придем к шестому, наиболее простому приближению лучистой теплопроводности (ЛТП). В оптически прозрачных средах приближения ДФ и ЛТП дают завышенные значения потока излучения, поэтому при расчете с ними желательно ограничивать тепловой поток предельно допустимым значением. В рассмотренной в следующем разделе задаче значения теплового потока не превышают предельно допустимые значения из-за достаточной оптической плотности системы.

P1 модель, в отличие от ДФ и ЛТП приближений, сохраняет конечной скорость распространения фотонов, которая в общем случае меньше скорости света. Это исправлено в P1/3 приближении, предложенном в работе [18] введением множителя 1/3 перед производной потока по времени. Путем асимптотического анализа Г. Морел показал [20] , что характеристики моделей при P1/3 и P1 приближениях близки.

Далее представляются результаты как в Р1, так и в P1/3 приближении. КД приближение учитывает кинетические эффекты за счет использования коэффициентов, являющихся дробно-линейными функционалами решения, что делает его наиболее близким к кинетической модели. Алгоритмы решения уравнения переноса тепла излучением для моделей с разными приближениями описаны в работах [21, 22] . Метод решения уравнения ЛТП взят из [14] .

• 3.    Постановка тестовой задачи

  Рассматривается шар радиусом 0 <  r <  R 2 , состоящий из двух физических областей (Табл. 1) . Внутреннюю область 1 (0 < r < R1) образует вещество плотностью р 1 = 0.02 г/см ³ , внешнюю область 2 (R 1 <  r < R2) — вещество плотностью р ₂ = 1 г/см ³ . Уравнение состояния каждого из веществ представляется как P = 0.54pT и E = c v T , где c v = 0.81T — постоянная теплоемкость. Шар, как система, имеет начальную температуру T ⁰ = 0.00001 кэВ,

начальную скорость u = 0. На внешней границе системы задано давление в условных единицах (1 у.е.= 108 ТПа) P r ₂ =0.1 у.е. и температура T R 2 =0.1 кэВ. Постановка задачи описана в работе [11] , но здесь для упрощения коэффициент поглощения взят одинаковым в обеих областях. Коэффициент поглощения вычисляется по формуле: a c = ( р/ 5) [(1 + 8.65/ ( p ^2/3 T2 )) ^3/2 — 1], коэффициент рассеяния — по формуле: a s = р/5.

Таблица 1. Состав системы

Параметр	Номер области
	1	2
Начальная плотность ρ 0 , г/см 3	0.02	1
Начальные радиусы R 1,2 , см	0.5	0.6
Число ячеек разностной сетки	100 x 30	400 x 30

При численной реализации расчетная разностная сетка выбирается исходя из данных о сходимости к точному решению. До выхода на стационарный режим все величины являются осциллирующими функциями, и при t → ∞ решение задачи выходит на постоянные значения:

u = 0, P =1 ТПа, T = 0.1 кэВ, R i,st = R 1 3 р 0 р ^. « 0.11 см,

R 2,st = з/ (1/p st )[R1p1 + (R2 — R 3 ) p 2 ] « 0.37 см, P1 , 2 = P st « 1.851 г/см3.

Нижний индекс st указывает, что величина отвечает стационарному режиму.

• 4.    Результаты моделирования

Расчеты проводились по двумерной программе, разработанной авторами в РФЯЦ-ВНИИТФ для осесимметричной цилиндрической геометрии до времени достижения максимальных значений плотности и температуры в 1-й области (0.13 мкс). Далее, с течением времени происходит изменение значений плотности и температуры в виде пульсаций с выходом на стационарный режим.

Константа сходимости итераций по температуре полагалась равной 10 ^{- 5} , квадратура по направлениям полета частиц — ES16. Шаг по времени варьировался с учетом поведения решения, но не превышал 1 пс.

Максимальные значения основных газодинамических величин (температуры, давления и плотности) достигаются в центре сферы. Данные расчетов, а именно, максимальные значения средней температуры Tmax и средней плотности в 1-й области, времена счета на ЭВМ (tCP), прихода тепловой (tTW) и ударной (tSW) волн в центр сферы и их отличия ∆в процентах от результатов по кинетической модели приведены в таблице 2. Средняя плотность и температура вещества вычисляются по формулам р = ^i p i V i / ^iV i , T = ^i T i M i / ^pMi , где ρ _i и T _i — плотность и температура в центре ячейки с индексом i, имеющей объем V _i и массу M _i .

Таблица 2. Результаты расчетов

Модели	T m1 ax ,кэВ	∆T max ,%	ρ 1max ,г/см 3	∆ρ max ,%	t TW ,мкс	∆t CP ,%	t SW ,мкс	∆t SW ,%	t CP ,час
Кинетическая	0.41036	0	89.04680	0	0.67964	0	0.82870	0	24
КД	0.41247	0.52	88.18494	0.97	0.68594	0.93	0.82520	0.42	11
ПКД	0.41248	0.52	88.20339	0.95	0.68595	0.93	0.82526	0.42	11
Р1	0.41134	0.24	88.68709	0.40	0.68594	0.92	0.82536	0.40	2
Р1/3	0.41134	0.24	88.69607	0.39	0.68595	0.93	0.82537	0.40	2
ДФ	0.41134	0.24	88.70132	0.39	0.68595	0.93	0.82536	0.40	2
ЛТП	0.40294	1.80	80.57137	9.52	0.66174	2.63	0.82142	0.99	0.5

Из таблицы 2 видно, что все приближения, кроме ЛТП, показывают достаточно хорошее согласование (разница менее 1%) с кинетической моделью по рассматриваемым величинам. Самой затратной по времени счета является кинетическая модель, хотя в ней применяется распараллеливание по направлениям полета фотонов. Наиболее экономичным выглядит приближение ЛТП, однако оно дает максимальные отличия от кинетической модели. Выход на стационарный режим через 10 мкс для различных приближений происходит быстрее, по сравнению с кинетическим расчетом, примерно от 2 до 50 раз, поэтому рационально использовать именно приближенные модели.

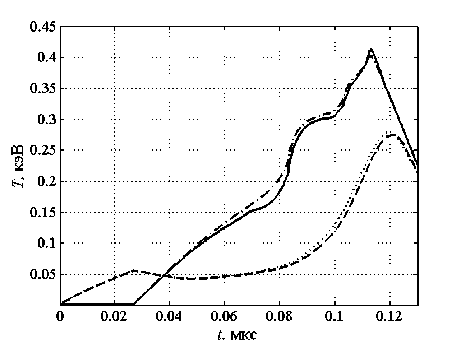
Поскольку для анализируемых далее результатов используемые модели переноса, за исключением ЛТП, дают визуально неразличимые графики, то для сравнения на рисунках представляются только приближения ЛТП и КД. На рисунке 1 приведены зависимости от времени средних по областям плотности и температуры веществ. Видно, что за все время расчета оба приближения хорошо согласуются по средним температурам и средним плотностям. Наибольшее отличие наблюдается при прогреве 1-й области, где разница в данных ЛТП и КД в момент времени 0.075 мкс составляет 10%. Однако ко времени 0.113 мкс при достижении средней температурой максимума расхождение уменьшается до 1.8%. Также отметим, что по средним плотностям имеет место расхождение в момент максимального сжатия 1-й области 0.117 мкс: разница между плотностями, найденными по приближениям ЛТП и КД равняется примерно 9%.

Как показано в работе [11] , рассматриваемая система является оптически плотной, поэтому в разных моделях средние по областям температуры вещества и средние радиационные температуры не отличаются в течение всего времени счета. Однако в отдельных точках, в частности, в центре сферы, они могут быть очень разными, то есть происходит «отрыв» температур.

«Отрыв» температур в моменты прихода ударных волн в центр сферы (0.0832 и 0.1125 мкс) демонстрирует рисунок 2. Из рисунка следует, что температура вещества практически мгновенно — за время 0.4 нc, вырастает на первом пике более чем в 10 раз (c T ≈ 0.3 кэВ до T ≈ 3.9 кэВ) и превышает радиационную температуру T r ≈ 0.65 кэВ более чем в 6 раз. Для анализа поведения ударной и тепловой волн на рисунке 3 в полулогарифмическом масштабе представлены профили основных термодинамических величин в разные моменты времени: при подходе тепловой волны к контактному разрыву — 0.025 мкс; при подходе тепловой волны к центру системы — 0.065 мкс; в момент, следующий за временем отражения ударной волны от центра сферы, — 0.088 мкс. Контактный разрыв изображен вертикальной штрихпунктирной линией и ему отвечают расстояния до центра сферы R= r ² +z ² соответственно, см: 0.1047; 0.2621; 0.4987.

На рисунке 3а приведены зависимости от расстояния до центра системы R профилей T , P , ρ в момент времени, близкий к приходу тепловой волны к контактному разрыву. Видно, что можно выделить четыре зоны: зону невозмущенного холодного вещества (0 < R < 0.498 см, ρ= 0.02 г/см ³ , T = 10 ^{- 5} кэВ, P = 10 ^{- 7} у.е.); зону предвестника ударной волны (0.498 < R< 0.506 см, 0.02 < ρ < 1 г/см ³ , T ≈ 10 ^{- 5} кэВ, P ≈ 10 ^{- 5} у.е.); зону ударной волны (R ≈ 0.506 см); прогретую за ударной волной зону (0.506 < R < 0.535 см, ρ ≈ 4 г/см ³ , 0.05 < T < 0.1 кэВ, P ≈ 0.1 у.е.). При этом фронты тепловой и ударной волн совпадают.

Рисунок 3б содержит профили T, P, ρ в момент времени, близкий к приходу тепловой волны в центр системы. На графиках можно выделить шесть зон: зону невозмущенного холодного вещества (0 < R< 0.07 см, ρ = 0.02 г/см ³ , T = 10 ^{- 5} кэВ, P = 10 ^{- 7} у.е.); зону предвестника ударной волны, где температура превышает граничное значение (0.07 < R < 0.21 см, ρ = 0.02 г/см ³ , T ≈ 0.15 кэВ, P ≈ 10 ^{- 3} у.е.); зону ударной волны (R ≈ 0.21 см); зону волны разрежения при (R ≈ 0.3 см); зону между ударной волной и волной разрежения (0.21 < R < 0.3 см); зону перед волной разрежения (0.3 < R < 0.41 см). При этом фронт тепловой волны опережает фронт ударной волны примерно на 0.14 см. Рост температуры выше граничного значения в зоне между тепловыми волнами

( a )

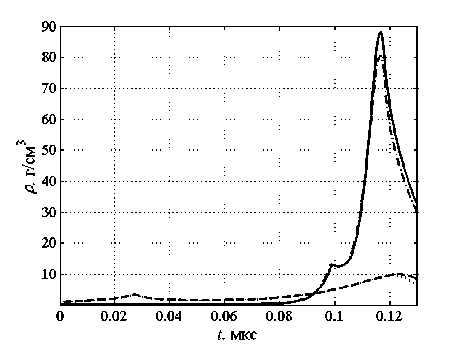
Рис. 1. Зависимости от времени средних значений температуры ( а ) и плотности ( б ) для двух приближений переноса тепла излучением: 1-я область – ЛТП (штрихпунктирная линия), КД (сплошная); 2-я область – ЛТП (точечная линия), КД (штриховая)

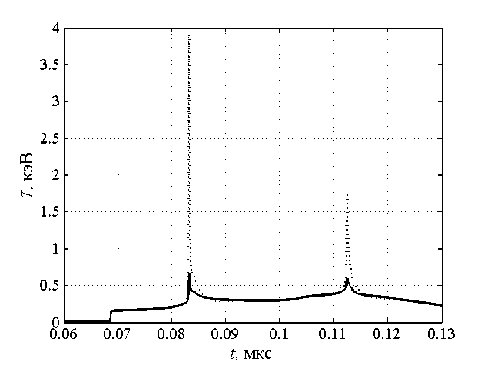
Рис. 2. Температуры в центре сферы для КД приближения: температура вещества (точечная линия), радиационная температура (сплошная линия)

(0.07 < R < 0.3 см) объясняется переходом части кинетической энергии в тепловую за счет сжатия вещества.

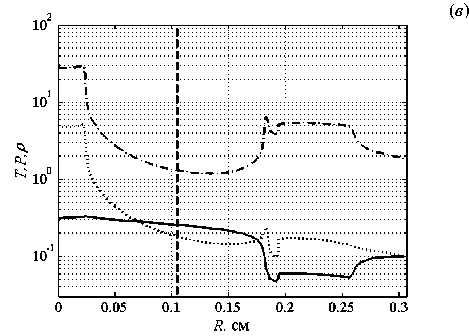
Рисунок 3в демонстрирует профили T, P, ρ после отражения ударной волны от центра. Просматриваются три зоны: зона после прохождения отраженной ударной волны (0 < R < 0.025 см); зона от отраженной тепловой волны до отраженной ударной волны (0.025 < R < 0.185 см); зона перед отраженной тепловой волной (0.185 < R < 0.31 см). После отражения ударной волны от центра система полностью прогрелась, и фронт отраженной тепловой волны опережает фронт отраженной ударной волны примерно на 0.17 см. Вторичные волны нагрева и сжатия во 2-й области шара создают немонотонную картину поведения величин T , P , ρ в третьей зоне.

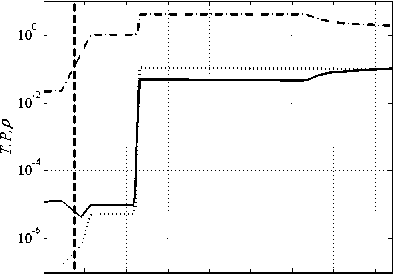
0.495 0.5 0.505 0.51 0.515 0.52 0.525 0.53 0.535

( а )

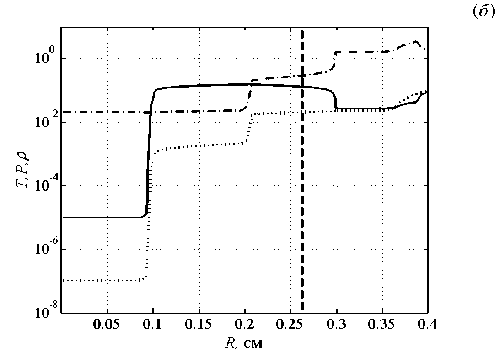
Рис. 3. Фронт ударной волны (вертикальная штриховая линия) и профили температуры T (сплошная линия), давления P (пунктирная), плотности ρ (штрихпунктирная) в КД приближении в разные моменты времени, мкс: 0.025 ( а ); 0.065 ( б ); 0.088 ( в )

Л. см

• 5.    Заключение

В работе проведено тестирование различных приближенных моделей переноса тепла излучением на задаче сжатия сферической системы ударными волнами. Приведены результаты расчетов, направленных на нахождение максимальных значений плотностей и температур как в центре сферы, так и их средних значений по областям, а также на определение времен прихода ударной и тепловой волн в центр системы. Исследовано прохождение ударной и тепловой волн через контактный разрыв и их поведение до и после фокусировки в центре системы. Показано, что задачи подобного типа можно значительно быстрее решать по упрощенным моделям.

Полученные результаты позволяют сделать следующие выводы:

• 1)    Средние по веществам температуры и плотности совпадают во всех моделях с точностью до 1%, за исключением ЛТП. В приближении ЛТП в момент максимального сжатия отличие от кинетической модели по средней плотности в 1-й области достигает 9.5%, максимальной средней температуры — 1.8%.

• 2)    Эффект «отрыва» температуры наблюдается только в точках максимального сжатия во всех моделях, кроме ЛТП, где он не возможен. Температура вещества в точках максимального сжатия может превышать радиационную температуру более чем в 6 раз.

• 3)    Диапазон времени прихода в центр системы тепловой волны согласно рассмотренным моделям, кроме ЛТП, достаточно небольшой, примерно 0.6 нс, времени прихода ударной волны примерно — 0.4 нс. В приближении ЛТП время прихода в центр, в сравнении с кинетической моделью, меньше примерно на 2 нс у тепловой волны и примерно на 0.7 нс у ударной волны.

• 4)    К моменту подхода ударной волны к контактному разрыву и к центру системы можно выделить зону теплового предвестника. В этом заключается отличие описанной тестовой постановки от классических постановок таких ударно-волновых задач, как пробивание, ударно-волновое нагружение, откольные явления и других, где теплопроводность не играет значимой роли.

• 5)    Хотя в сферических слоях степень кумуляции может быть значительно выше, чем в плоских, учет теплового излучения в данной задаче дает конечную плотность и температуру в момент фокусировки, что подтверждается расчетами в моделях разной степени приближения.

• 6)    До момента фокусировки в центре системы перед ударной волной в 1-й области за счет излучения появляется зона прогрева, в которой вещество достигает температуры выше граничной. В момент фокусировки в центре системы температура вещества увеличивается более чем в 10 раз.

• 7)    В обсуждаемой задаче время счета в КД и ПКД приближениях примерно в два раза меньше времени счета по кинетической модели (с учетом распараллеливания по направлениям полета фотонов), в ДФ, Р1 и Р1/3 приближениях — в 12 раз меньше, в ЛТП приближении — в 48 раз меньше.

• 8)    Совпадение результатов расчета по кинетической модели и в ДФ приближении показывает достаточно хорошую точность и монотонность кинетической схемы TVDR (Total Variation Diminishing Reconstruction) [21] повышенного порядка аппроксимации, поскольку в ДФ приближении используется схема второго порядка аппроксимации по пространству [22] . Классическая монотонная схема первого порядка аппроксимации для кинетической модели дает отличие от схемы TVDR по времени прихода тепловой волны в центр системы около 26% [12] .

Тестовая задача и результаты, полученные авторами, могут использоваться для исследования процессов сжатия веществ ударными волнами и тестирования методик высокотемпературной газовой динамики, учитывающих перенос тепла излучением в различных приближениях.