Распределение ресурсов типа мощности на основе обобщения задачи о "редакторе"

Строительное производство многовариантно по своей природе: существует достаточно большое количество возможных вариантов возведения объекта. Связано это не в последнюю очередь с ограниченными ресурсами, имеющимися в распоряжении любой строительной организации и договорными сроками, которых необходимо придерживаться. В том случае, когда строительная организация не в состоянии обеспечить выполнение производственной программы в заранее оговоренные сроки, предполагается привлечение сторонних организаций, называемых субподрядными, для участия в строительстве объекта. В этом случае возникает задача определения эффективной политики взаимодействия с субподрядными организациями.

При этом, как правило, считаем, что ресурсы строительной организации являются ограниченными, а ресурсы привлекаемых предприятий нет, что для практики является достаточно характерным, так как возможно привлечение нескольких организаций, ресурсы каждой будут также ограничены.

Возможно более простое представление производственного процесса: представить все множество работ в виде двух укрупненных комплексов. Причем порядок чередования работ генподрядной и субподрядной организации в различных задачах может быть различным [1]. Такое представление достаточно выгодно, так как позволяет исходную задачу в самом простом случае привести к известной классической задаче Джонсона о двух станках.

Управление в социально-экономических системах

Моделирование взаимодействия с субподрядными организациями

С точки зрения организации строительного производства наиболее целесообразным является разбиение всего множества работ, подлежащих выполнению на объектах, включаемых в производственную программу строительного предприятия, на три комплекса работ: первый – это работы по возведению каркаса здания, кровле и заполнению проемов, второй – внутренние работы и третий – подготовка к сдаче объекта. Наиболее вероятно, что первый и третий вид работы могут выполняться одной и той же единицей ресурса, а второй вид работы – другим видом ресурса. Такая постановка задачи оказывается полностью соответствующей известной классической задаче «редактора» [2].

Допустим, в обработке находится n «рукописей». При этом следует пояснить, что в данном случае под этим термином будем понимать строящиеся объекты. Порядок работы с «рукописями» предполагается следующий: сначала каждая «рукопись» проходит первичное редактирование и возвращается авторам на доработку, после окончания которой вновь попадает для окончательного редактирования.

Введем обозначения: a i – продолжительность первого редактирования i -й рукописи, b i – продолжительность работы автора над i -й рукописью, τ i – продолжительность второго редактирования i -й рукописи. Необходимо найти такую очередность обработки рукописей, при которой общая продолжительность их обработки была минимальной.

Если ввести новые переменные 4 = т i - a i , q i = a i + bi [3, 4], то классическое решение задачи о «редакторе» будет следующим: сначала осуществляют обработку рукописей, для которых выполняется условие 4 >  0 в очередности возрастания q i , а затем - рукописей, для которых 4 <  0 в очередности убывания q i [2, 5].

Если предположить, что для выполнения первого и третьего вида работ имеется одна единица ресурса, а для выполнения второго вида работ n единиц ресурса, то в итоге получим задачу «редактора», в которой в качестве редактора выступает единица ресурса, выполняющего первый и третий вид работ, а в качестве авторов – единицы ресурса, реализующие второй комплекс работ. В том случае, когда полученная в результате расчета продолжительность строительства превышает допустимое значение, задаваемое договорными обязательствами, приходится решать вопрос о передачи части объектов сторонним организациям. Задача заключается в определении объектов, передаваемых сторонним организациям, обеспечивающим выполнение программы в заданные сроки при минимальном уровне дополнительных затрат.

Рассмотрим производственную программу строительного предприятия, данные о которой приведены в табл. 1.

Таблица 1

Данные об объектах строительства

i	Наименование объекта	Сметная стоимость, млн руб.	Директивный срок строительства, мес.
1	Расширение и реконструкция лечебного корпуса госпиталя ФКУЗ «МСЧ МВД России по Воронежской области»	507,1	34
2	Строительство комплекса зданий отдела МВД России по Новохоперскому району г. Новохоперск, ул. Плотникова, 2б	306,0	29
3	Реконструкция административных зданий отдела МВД России по Лискинскому району Воронежской области, г. Лиски, пл. Революции, 3а	152,0	21
4	Строительство изолятора временного содержания отдела МВД России по Бобровскому району, г. Бобров, ул. Кирова, 25	117,4	17

Для расчета общей продолжительности проекта удобно воспользоваться матричным способом увязки потоков [5]. При осуществлении расчета будем придерживаться правила, согласно которому ресурсы для выполнения работ второго типа не ограничены, и главное при увязке потоков обращать внимание только на открытие фронта работы. Исходные данные и результаты расчета приведены в табл. 2, 3.

Таблица 2

Исходные данные для задачи

i	I	II	III	IV
а i	16	12	8	7
b i	11	9	7	6
τ i	7	8	6	4
c i	43	28	15	11

Таблица 3

Матричный способ расчета

0 16 16	16 11 27	43 7 50
16 12 28	28 9 37	50 8 58
28 8 36	36 7 43	58 6 64
36 7 43	43 6 49	64 4 68

Учитывая, что по условию, общая продолжительность выполнения всего проекта не должна превышать 46 мес., приходим к заключению, что необходимо принимать меры к уменьшению общей продолжительности строительства, то есть передать возведение части объектов сторонним организациям. Таким образом, задача заключается в том, чтобы уложиться в заданные сроки при минимальных дополнительных затратах. Передача части объемов работ сторонним организациям может происходить двумя способами:

• 1)    передача всего объекта сторонней организации;

• 2)    передача отдельных объемов работ, выполняемых на отдельных объектах сторонней организации.

В первом случае необходимо составить зависимость сроков строительства от дополнительных затрат. Для этого случая необходимо определять продолжительность выполнения всего комплекса объектов для случаев исключения одного или нескольких объектов из производственной программы предприятия. Повторив такой расчет, получим результат, представленный в табл. 4.

Таблица 4

Зависимость дополнительных затрат от сроков строительства

Объекты	0	IV	III	IV и III	II и IV	I и IV
Срок строительства, мес.	68	57	54	45	40	35
Дополнительные затраты, млн руб.	0	11	15	26	39	54

При построении таблицы учитывалось явление доминирования решений: в итоговую таблицу включались только наиболее перспективные решения.

Таким образом, при заданном директивном сроке в 46 мес. к наименьшим затратам приведет передача сторонним организациям третьего и четвертого объектов, что, как уже говорилось, сократит срок строительства до 45 мес., при этом размер дополнительных затрат составит 26 млн руб. Столбец табл. 4, соответствующий решению, выделен цветом.

Алгоритм решения задачи

Для реализации второго варианта сокращения сроков строительства произведем разбивку совокупных дополнительных затрат, приведенных по объектам по видам работ пропорционально продолжительности их выполнения. Результаты представлены в табл. 5.

Управление в социально-экономических системах

Для решения задачи второго типа, то есть задачи об определении объемов отдельных работ, передаваемых на выполнение сторонним организациям, необходимо построить сетевой график рассматриваемого процесса и найти в нем критический путь. Построенный график, описывающий данный способ организации работ, приведен на рис. 1, критический путь выделен жирными линиями. Легко подсчитать, что его длина равна 68 мес., что больше директивного срока на 22 мес. Для дальнейшего решения вычислим эффективности каждого вида работ при передаче сторонним организациям в целях сокращения продолжительности выполнения проекта в целом. Результаты приведены в табл. 6 (работы с наибольшей эффективностью выделены цветом).

Таблица 5

Разбивка затрат по видам работ

i	I	II	III	IV
c i 1	20	12	6	5
c i 2	14	9	5	4
c i 3	9	8	4	3
с i	43	28	15	11

Таблица 6

Эффективности работ

i	I	II	III	IV
а i	16	12	8	7
c i 1	14	9	5	4
Эффективность	1,14	1,33	1,60	1,75
b i	11	9	7	6
c i 2	14	9	5	4
Эффективность	0,79	1,00	1,40	1,50
τ i	7	8	6	4
c i 3	9	8	4	3
Эффективность	0,78	1,00	1,50	1,33

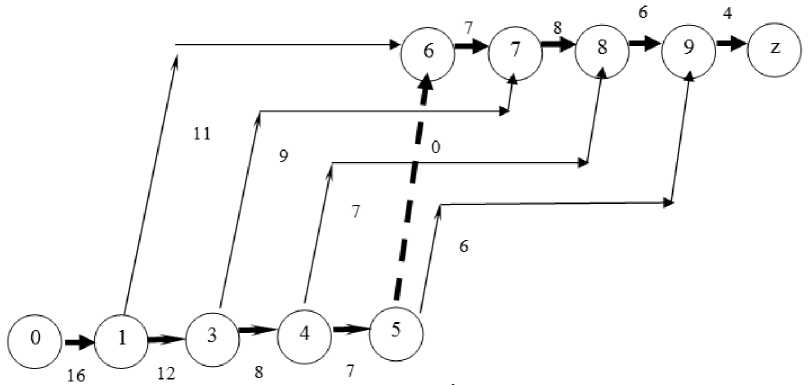
Рис. 1. Сетевой график задачи о «редакторе»

k -й шаг. Выбираем работу, лежащую на критическом пути, имеющую наибольшую эффективность. Согласно данным табл. 5, такой работой является работа первого вида на четвертом объекте. Положим продолжительность этой работы в сетевом графике равной нулю и найдем критический путь, так как в результате изменения продолжительности одной из работ, лежащей на критическом пути он может измениться. В данном случае он не изменился, но его длина стала равна 61 мес., что превышает директивные сроки, поэтому повторяем шаг. Следующей по эффективности является работа первого вида на третьем объекте. Передача этой работы сторонним организациям должна была бы привести к уменьшению срока строительства на 8 мес., но при таком изменении происходит и изменение критического пути, длина которого становится равной 55 мес. (результаты этого шага приведены на рис. 2), что по-прежнему превышает необходимое значение, поэтому повторяем шаг.

В данном случае на критическом пути будет находиться работа третьего вида на третьем объекте. Ее передача сторонней организации сократит срок строительства до 49 мес., и критический путь не изменится. Необходимое значение еще не достигнуто, поэтому повторяем процедуру.

В данном случае перспективным для включения в решение является третий вид работы на четвертом объекте. Величина критического пути составит 45 мес. Результат приведен на рис. 3. Так как величина продолжительности выполнения всего проекта достигла нормативной величины, то переходим к следующему шагу.

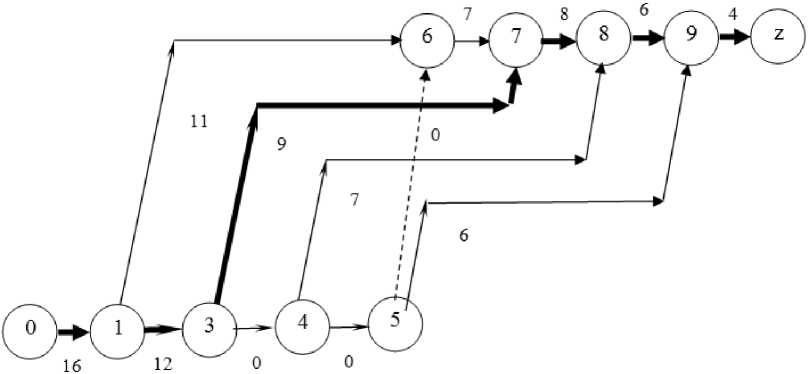
Рис. 2. Сетевой график задачи о «редакторе» после двух шагов

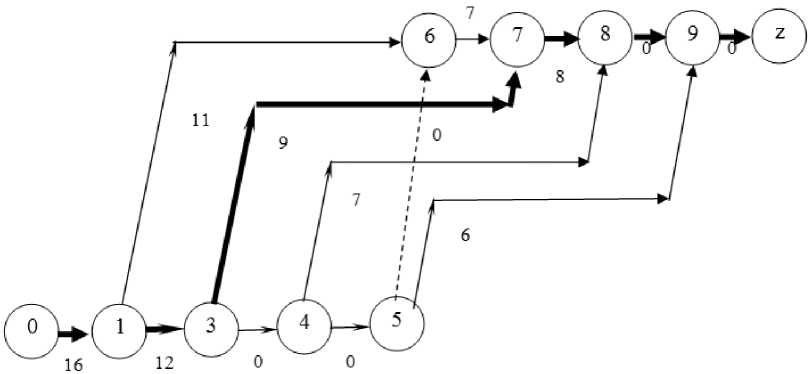
Рис. 3. Результат решения задачи о «редакторе»

k + 1-й шаг. Используя данные, полученные на предыдущем шаге, и табл. 5, формируем окончательное решение: для выполнения сторонним организациям передаются работы первого и третьего вида на третьем и четвертом объектах, что приведет к дополнительным затратам в размере c31 + c41 + c33 + c43 = 5 + 4 + 4 + 3 = 16 млн руб.

При этом общая продолжительность строительства будет составлять 45 мес., что согласуется с заранее определенными договорными сроками.

Алгоритм решения задачи с учетом ограничений на ресурсы второго типа

Теперь рассмотрим случай, когда техническое оснащение предприятия имеет другую направленность: ресурсов для выполнения работ первого и третьего вида достаточно, чтобы обеспечить их параллельное выполнение, а вот ресурсы для выполнения работ второго вида ограничены, и предприятие может обеспечить только последовательное выполнение таких работ. Обозначим через a i , b i , τ i продолжительности выполнения работ на i -м объекте, соответственно, первого, второго и третьего видов.

Управление в социально-экономических системах

В данном случае легко определить, что начало работ второго типа на i -м объекте будет равно [5] d i = a i + 1, а поздний момент окончания равен D i = T – τ i .

Таким образом, работы второго вида на i -м объекте должны быть выполнены на отрезке времени [ d_i ; D_i ]. Для решения задачи применяем потоковую модель. Для этой цели примем, что временной отрезок, задаваемый договорными сроками [0; Т д ], разбит на m отрезков постоянства уровней ресурсов. Обозначим N k – количество ресурсов в k -м интервале. Кроме того, примем, что работа i может выполняться в промежутке от момента времени d_i до D_i включительно. Предполагаем, что имеет место линейная зависимость продолжительности выполнения работы от количества ресурса, назначенного для ее выполнения. Расположим работы по убыванию величины дополнительных затрат с i .

Определим сеть из ( n + m + z + 1) вершин, состоящую из входа 0, n вершин первого слоя, m вершин второго слоя и выхода z . На рис. 4 приведен пример такой сети для случая n = 4, m = 6.

Вершина 0 соединена со всеми вершинами первого слоя дугами (0, i ) пропускной способности P °i = W i [6, 7]. Вершина i первого слоя соединена с вершиной j второго слоя дугой ( i , j ), если работа i может выполняться в интервале j . Пропускная способность дуги ( i , j ) равна p j = a i A j , где A j - длительность интервала j .

Наконец, каждая вершина j второго слоя соединена с вершиной z дугой ( j , z ) пропускной способности P jz = A j N j . Определим поток { x j } в сети следующим образом [8, 9]:

0 ^ x о i 5 W i , i = 1, n , ° 5 x j 5 P j , i = 1, n , j = 1, m ,

• ^{0 5} x jz ⁵ P jz , ^j = 1, m , Z x j = ^x ° i , i = 1, n ,

j' eRi где Ri – множество дуг, исходящих из вершины i первого слоя.

• Z x ij = x jz , ^j = 1, m ,

ie PJ где Рj – множество дуг, заходящих в вершину j второго слоя.

Заметим, что любому потоку { x_i j } однозначно соответствует допустимое распределение объемов работ по периодам. И наоборот, любому допустимому распределению работ по периодам однозначно соответствует поток в сети.

Задача заключается в определении потока, минимизирующего

C ^{( x} ) = Z ( w - ^x 0 i ) c i ,

i где wi – объем работы.

Рассмотрим описание алгоритма [9, 10].

1-й шаг. Вычисляем поток максимальной величины, проходящей по дуге (0, 1) первого слоя.

2-й шаг. Находим поток максимальной величины, проходящей по дуге (0, 2) первого слоя и не уменьшающей величины потока по дуге (0, 1) первого слоя.

k -й шаг. Получаем поток максимальной величины, проходящей по дуге (0, k ) первого слоя и не уменьшающей величины потоков по дугам (0, i ) первого слоя ( i <  k ).

Теорема [7]. Описанный выше алгоритм дает оптимальное решение задачи.

Доказательство . Поток по любой дуге (0, k ) первого слоя можно увеличить только за счет уменьшения на ту же величину потоков по дугам (0, i ) первого слоя, где i <  k . Но это не приведет к уменьшению затрат, поскольку C i >  C k для всех i <  k . Это доказывает теорему.

Разница в том, что для выполнения работ второго вида имеется только одна единица ресурса. Поэтому пропускные способности c 0 i = a i , c ij = Δ ij , c jz = Δ j , i = 1, …, m , где m – число интервалов.

По-прежнему директивный срок выполнения всего проекта составляет Т _д = 46 мес.

Вычислим интервалы [ d_i ; D_i ] производства работ. Результаты приведены в табл. 7 и 8.

Таблица 7

Исходные данные для задачи

i	I	II	III	IV
а i	16	12	8	7
b i	11	9	7	6
τ i	7	8	6	4
c i	43	28	15	11

Таблица 8

Возможные интервалы выполнения работ

i	I	II	III	IV
d i	17	13	9	8
D i	39	38	40	42

Таким образом, работы второго вида должны начинаться и оканчиваться в интервале от 8 до 42 мес. Выделим шесть интервалов, длительности которых равны 6. Таким образом, вершине 1 будет соответствовать временной интервал [8; 13], вершине 2 – [14; 19], вершине 3 – [20; 25], вершине 4 – [26; 31], вершине 5 – [32; 37], вершине 6 – [38; 42]. Таким образом, пропускные способности дуг, входящих в вершины второго слоя с номерами 1–5 будут иметь пропускную способность, равную 6, а для 6-й вершины этого же слоя – 5.

Решение задачи строится таким образом, что нам необходимо распределить поток, входящий в вершины первого слоя через дуги, соединяющие вершины второго слоя. Естественно, что в первую очередь стараемся распределить те объемы работ, передача которых сторонним организациям будет наиболее затратной. Для этой цели удобно исходные данные расположить в порядке убывания дополнительных затрат.

Потоковая сеть приведена на рис. 4.

Рассматриваем объект, на котором могут быть начаты работы. Такой объект единственный – четвертый, работы второго вида на этом объекте должны быть выполнены в промежутке [8; 42] и их длительность составляет 6 мес. Соответственно соединяем дугой четвертую вершину первого слоя и первую вершину второго слоя. Дуга при этом получается насыщенной. Во временной интервал соответствующий второй вершине второго слоя можно начать работы на втором объекте, поэтому соединяем вершину два первого слоя с вершинами два и три второго слоя и т. д. В итоге получаем, что заданный объем работ может быть полностью выполнен собственными силами.

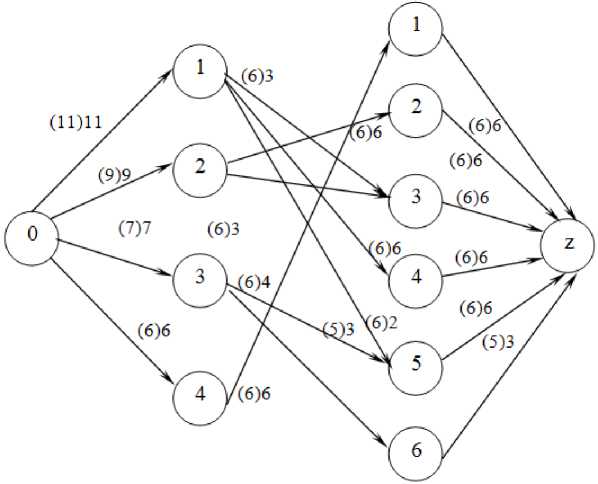
Рис. 4. Потоковая модель при Т _д = 46 мес.

Рассмотрим случай, когда директивный срок реализации всего проекта уменьшается до 40 мес. Это приведет к изменению интервалов времени, в которые могут быть реализованы работы на объектах, пересчитаем их, а результаты сведем в табл. 9.

Учитывая данные табл. 9, определяем возможные интервалы выполнения работ на всех объектах:

I объект – [17; 33]; II объект – [13; 32]; III объект – [9; 34]; IV объект – [8; 36].

Управление в социально-экономических системах

Таблица 9 Возможные интервалы выполнения работ при Т _д = 40 мес.

i	I	II	III	IV
d i	17	13	9	8
D i	33	32	34	36

Выделим семь интервалов, ширина которых будет равна 4: [8; 11], [12; 15], [16; 19], [20; 23], [24; 27], [28; 31], [32; 36]. Ширина последнего интервала составит 5.

Совершенно аналогично построим сетевую модель, необходимую для решения задачи, только выделив уже семь интервалов. Результат построения приведен на рис. 5.

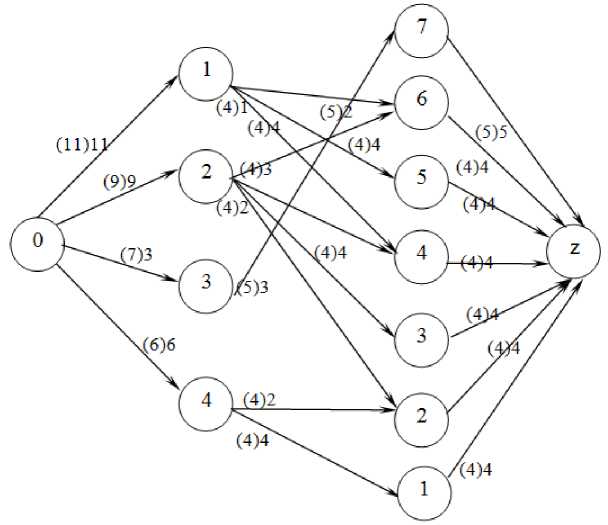
Рис. 5. Потоковая модель при Т д = 40 мес.

Анализируя построенную потоковую модель, можно убедиться, что при данном способе организации выполнения производственной программы предприятия, уложиться в директивные сроки не представляется возможным, поэтому часть третьего объекта, а именно 4/7 части объекта необходимо передать сторонним организациям. При этом затраты составят 4/7 · 15≈8,57 млн руб.

В данном случае мы допустили передачу части работ на третьем объекте для выполнения сторонней организацией. Если такая передача части работ недопустима, то задача становится существенно сложнее и в настоящее время не решена.

Обобщая полученные результаты, можно сформулировать следующее эвристическое правило, позволяющее получать последовательности объектов, близкие к оптимальным по срокам выполнения работ.

Эвристическое правило. Для получения рационального расположения объектов в потоке необходимо начинать объект, у которого наименьшая продолжительность выполнения первого вида работы, а заканчивать объектом, у которого наименьшая продолжительность третьего вида работы; остальные объекты выстраиваются в порядке возрастания продолжительности выполнения первого вида работы.

Выводы

В результате проведенного анализа была выявлена необходимость разработки комплекса эффективных моделей и алгоритмов оптимизации объемов работ по проекту с определением ра- циональных объемов работ, подлежащих выполнению собственными силами и передачи субподрядчикам. Подчеркивается, что строительные предприятия, выполняющие функции генерального подрядчика, координируют и контролируют выполнение работ и соблюдение всех необходимых регламентов привлеченными в качестве субподрядчиков предприятиями. Вполне понятно, что мероприятия, направленные на сокращение сроков выполнения проекта с целью выполнения договорных обязательств, с неизбежностью ведут к возникновению дополнительных затрат, направленных на реализацию такого сокращения. Данное обстоятельство приводит к возникновению класса задач выбора вариантов производства работ по проекту, обеспечивающих соблюдение договорных сроков при минимально необходимом удорожании.

В работе был рассмотрен случай, когда организационно-технологическое решение по возведению объектов, составляющих производственную программу предприятия, предполагает разбивку всех работ на объектах на три укрупненных комплекса работ, тогда стратегия технического оснащения предприятия приобретает направленность, связанную с накоплением ресурсов для выполнения работ первого и третьего вида с целью обеспечения их параллельного выполнения. В тоже время ресурсы для выполнения работ второго вида могут быть ограничены, и предприятие должно обеспечить только последовательное выполнение таких работ. В этом случае производственная программа предприятия может быть выполнена без передачи объектов сторонним организациям, то есть без дополнительных затрат.