Распространение гармонических волн в цилиндрической панели с учетом вязкоупругих свойств материала

Волновые процессы в волноводах в виде упругих цилиндрических изотропных и анизотропных оболочек постоянной толщины хорошо изучены [1, 2, 3]. Большое количество работ посвящено динамике оболочек, описанных на основе модели Тимошенко [4, 5, 6, 7]. В работе [8] для исследования волновых процессов применяются асимптотические методы волновых процессов в цилиндрической оболочке с малым изменением ее толщины вдоль оси. Вместе с тем задача исследования распространения волн в вязкоупругой цилиндрической панели с переменной толщиной представляет теоретический и практический интерес.

Постановка волновой задачи

Рассматривается вязко-упругая бесконечная цилиндрическая панель толщиной h , плотностью ρ. В криволинейной ортогональной системе координат (α 1 ; α 2 ; z) при z = 0 оболочка занимает область

— ^ < а < +^; 0 < а2 < l;

hh

—  <  z <   .

Кривизны срединной поверхности z=0, равные k j = 0; k₂ = р соответствуют координатам α 1 и α 2 . В рамках гипотез Кирхгофа – Лява закон изменения компонент вектора перемещений u 1 ^(z), u 2 ^(z), w^(z) панели определяются следующими соотношениями [1, 2]: u 1(z = u - 9 ! z; u₂⁽ z = &  - 9 2 z; u₃^(z) = w, (1)

где u, v, w – компоненты вектора перемещений срединной поверхности; θ₁ , θ₂ – углы поворота нормали относительно осей α 1 и α 2 .

Для вывода уравнений, позволяющих исследовать толщину панели , использовался принцип возможных перемещений

δП = δТ, (2) где δП – вариация потенциальной энергии оболочки; δТ – виртуальная работа массовых сил инерции панели . В работе В.В Новожилова [1], с учетом соотношений (1), сделан вывод для получения следующего выражения исходя из линейной теории упругости

В П =

= j { T 1 * + т 2 & ₂ + s b 12 + м 1 X + (3)

F

+ M X₂ + 2 N d? } d a d a ,

тельная константа. Далее, применяя процедуру замораживания [10], заменим соотношения (5) приближенными вида

Е ф = e [ 1 - Г С (а-) - i Г S ( а ) ] ф = Е ф ,

где Т 1 , Т 2 , S, M 1 , M 2 , N – усилия и моменты; £ 1 , a e₁₂ , X 1, X 2, т — компоненты деформации срединной поверхности. В выражении (3) исключены члены, имеющие порядок .

Согласно [1] компоненты тангенциальной изгибной деформации срединной поверхности выражаются через ее перемещение и углы поворота нормали следующим образом:

d u

* 1 = ^; ^£ d a

8 ^

X 1 = ^;

d a ₁

^в1=Чг ;

d a 1

da ,

2 =7-- ⁺ k 2 w * 1

d a

d 3    d u

₁₂ = ; d a d a

d 0 ₂        d O ₂

=      ^{; T} =      ^;

d a ₂        д а 1

# 2 =

dw da 2

+ k₂ 0 .

ю где      Г C(а) = |R(т)cos^T dr ,

ю

Г S ( а ) = j R ( т ) sin ат d r , соответственно, 0

косинус и синус – образы Фурье ядра релаксации материала. В качестве примера вязкоупругого материала примем трехпараметрическое ядро релаксации R ( t ) = Ae ^в / 1^{1 a} , обладающее слабой сингулярностью [9]. Предполагается, что силы инерции по углам 0 и 0₂ малы и сравнены другими силами инерции. Учитывая это, если пренебречь инерцией поворота нормали, то виртуальную работу силы инерции оболочки можно представить в виде

В свою очередь, усилия и моменты связаны с компонентами деформации соотношениями, вытекающими из обобщенного закона Гука:

^T i = ~ ⁽ * 1 ⁺ v * 2 )

~~~

M1 = D(X1 -VX2), S = ^*12;N = Вт, где

~   Eh    ~ с =----т; d =;

1 - v ²         12(1 - v ²)

~~

~    Eh    ~

A =-------; В =;

2(1 + v )        12(1 + v )

в т =

= - j p h ( u B u + 0B0 + w B w ) d a d a. - ⁽⁶⁾

F

После подстановки выражения (3) и (6) в (2) и процедуры интегрирования по частям с

учетом (4) получаем систему уравнений жения в виде:

дви-

Е ^~ – операторный модуль упругости, который имеет вид [9]

^E ? ⁽ t ) = E 01

t

^ ( t ^)- f R E ^{( t - T}) ^ ^{( t} ) d ^T

; (5)

ф ( ) - произвольная функция времени; Re ( t — т ) — ядро релаксации; v - коэффициент Пуассона; E – мгновенный модуль упругости. Будем считать интегральные члены в (5) малыми, тогда функции ^ ( t ) = ^ ( t ) e ^{- a} t , где ^ ( t ) - медленно меняющаяся функция времени, а — действи-

d T da dT, da d Q da

Q 1

ds + da dS + da

, d Q 2

da

d M..

d a ₁ ;

d ² u

- Ph¹—, dt ²

+ k 2 Q 2 = ^{— p h}

-

kT = - p h

d 20 ’ dE d ² w ~dP

Q₂     M + 2   ' .

d a ₂     d a ₁

Альтернативные краевые условия свободного края, или жесткой заделки, при α 2 = 0, l имеют вид: свободный край

S = 0 ; T₂ = 0 ; M ₂ = 0; Q 2 = 0; (9)

жесткая заделка u=0,  0 =0, w=0, Q2=0.      (10)

Используя соотношения (4), (5), (7), (8), полную систему уравнений движения можно представить в виде восьми дифференциальных уравнений, размешенных относительно первых производных по а :

A

d и да₂

= т

T 2

= S - A

_ ди

— cv--- д а

;

c k w

D

д ^ да

— M2

д w

да

д ² w.

д а ² ;

1 _;

—0₂ + к₂ &

д S      , д ² и _ д² и     д Т

---= —ph —-— с--- — v-— да      д t2   да2   да дТ2 да

дQ 2 да

₇ д&  д S

' ph —5--- дt2  да

^{— к} 2 Q 2

, д ² w — д⁴ w   д ² М₂

■ ph —г + D--т — v---.²

дt ²      да ⁴      да ²

+ к₂т₂ ;

M = Q 2 — 2 B ^, д а          д а ²

где

_  Eh   —    Eh ³

с = ----; d = -------;

1 — v ²         12(1 — v ²)

Eh          Eh ³

A = -------; B = --------.

2(1 + v )        12(1 + v )

В случае бегущих вдоль а1 гармонических волн решения краевой задачи для системы (11) с краевыми условиями типа (9), (10) до- пускают разделение переменных:

„ i ( к а — a t )

u = Zj е v 1;

(12)

i (ка1 —at) w = z3e;

i ^{( к}а -t ) ).

2 z 4 e;

о _ _ i ^{( к}а -t ) ) .

^z  t^

7      ^ &i ^{( к} а^{— a t} )

T 2    z 6 e

0₂ = z₇ei ^{( к а} 1

— a t )

;

M2 = ze(ка1—at t- где a = a + ia — комплексная собственная частота; к - волновое число; a — действительная часть комплексной частоты; p -плотность; z].(а )(j — 1,2,3..8) - функции формы колебаний. Для выяснения их физического смысла рассматриваем случаи:

• 1)    к = k_r ; V = C_R + iC_/ - тогда решение (9) имеет вид синусоиды по z , амплитуда которой затухает по времени;

• 2)    к = k_r + к ; V = C_R - тогда в каждой точке решение (9) имеет вид синусоиды по t, амплитуда которой затухает по ^ 1 .

Далее предполагается, что оба края оболочки а₂ = 0 и а — l свободны. После подстановки соотношений (12) в уравнения (11), учитывая и краевые условия (9), имеем спектральную краевую задачу по параметру a для системы восьми обыкновенных дифференциальных уравнений относительно комплексной функции формы:

z 1 = z 5 /A + kz₂ , z₂ = z₆ /с +v кz_l — ка ,

'                                          '2

z3 — — z4 + k2z2, z4 = z8 / D — v к z3, z5 — h (Ек2 — pa )zj +vh2 z6, z, — — hpaz. — kz — kz ,

6             2     527

z₇ — — h pa^ z ₃ + E /12 h k z ₃ + v k ^ z ₈ + k₂z ₆;

z„ — z₂ + G 3h³ k ² z ₄ ;

^z 5    ^z 6    ^z 7     ^z 8     ^{0 ; а} 2 ^{— 0}, ^l .

При анализе дисперсии гармонических волн параметр к считается заданным.

Численный анализ дисперсии нормальных волн в цилиндрических панелях

На основе решения краевой задачи (13) методом ортогональной прогонки Годунова был выполнен численный анализ дисперсии этих волн.

На рис. 1 и 2 показаны зависимости действительных частей комплексных фазовых скоростей первых двух мод от волнового числа. Во всех вариантах расчета приняты следующие безразмерные параметры панели:

E — 1, p — 1, v — 0,25, i — 1 ,

A = 0,048; в = 0,05;   a = 0,1 .

Толщина h изменяется по линейному закону h( a ₂ ) = h 1 + Л И. a ₂,    (14)

Ah = (h - h ) /1 .

Сплошные линии на рисунках соответствуют вариантам панели постоянной толщины (h1= h2=0.1), пунктирные линии характеризуют панель с клиновидным сечением (Ah = 0.0001  ). В последнем случае h2=0.1, а толщина h1 =0.001. Параметры кривизны к2 постоянны и принимают значения 450 и 900. Штрихпунктирные линии на рис. 1 и 2 соответствуют рассмотренному случаю пластин Кирхгофа – Лява при к2=0. Из рис. 1 и 2 видно качественное отличие в поведении дисперсионных кривых первой моды, соответствующих оболочке и пластинке. Если во втором случае кривая фазовой скорости монотонна, то в первом случае наблюдается характерный максимум в средневолновом диапазоне, который объясняется повышенной изгибной жесткостью оболочки по сравнению с пластинкой.

Действительная часть скорости второй моды в отличие от случая панели постоянной толщины в целом также возрастает с ростом кривизны. При этом, как и следовало ожидать, чем больше кривизна к 2 , тем медленнее осуществляется переход на участок без дисперсионного движения ( c = const ) с ростом волнового числа. Что касается самой локализации, то она увеличивается с увеличением кривизны (при достаточно больших к , например, при к =10). Причем такая повышенная локализация в цилиндрической панели характерна для обеих мод (действительные части комплексной на скорость). С ростом параметра к 2 наблюдается тенденция увеличения скорости ( С ) изгибной моды и уменьшения скорости крутильной моды.

Скорости коэффициента затухания ( С ) изгибной моды уменьшаются по параметрам к 2 , а также увеличивается скорость затухания крутильной моды.

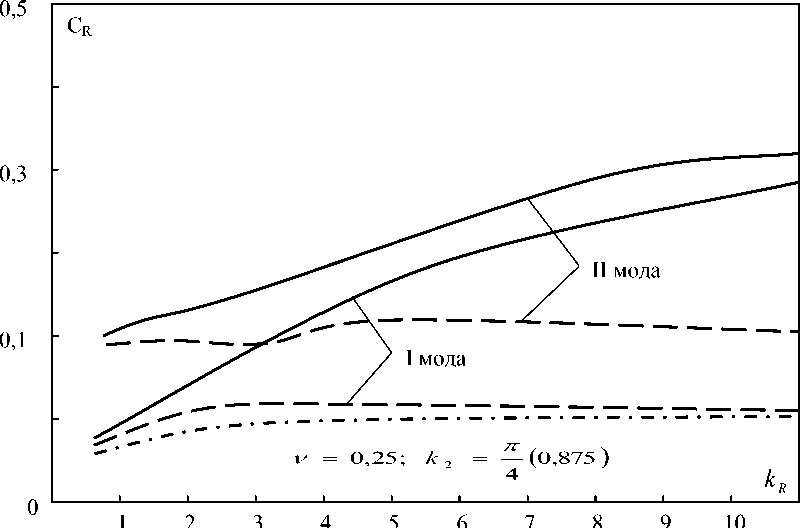
Рис. 1. Зависимость действительной части скорости (C_R ) распространения волны от волнового числа

Выводы

• 1.    С ростом кривизны цилиндрической панели постоянной толщины увеличивается действительная часть комплекса ( C_R = Re al ( V )) – скорость распространения первой изгибной моды и уменьшается скорость распространения второй крутильной моды.

• 2.    В случае клиновидной цилиндрической панели для каждой моды существуют предельные скорости распространения при увеличении волнового числа, совпадающие по величине с соответствующими скоростями нормальных волн в клиновидной пластине нулевой кривизны. В коротковолновом диапазоне локализация движения существует и увеличивается с ростом кривизны панели.

  

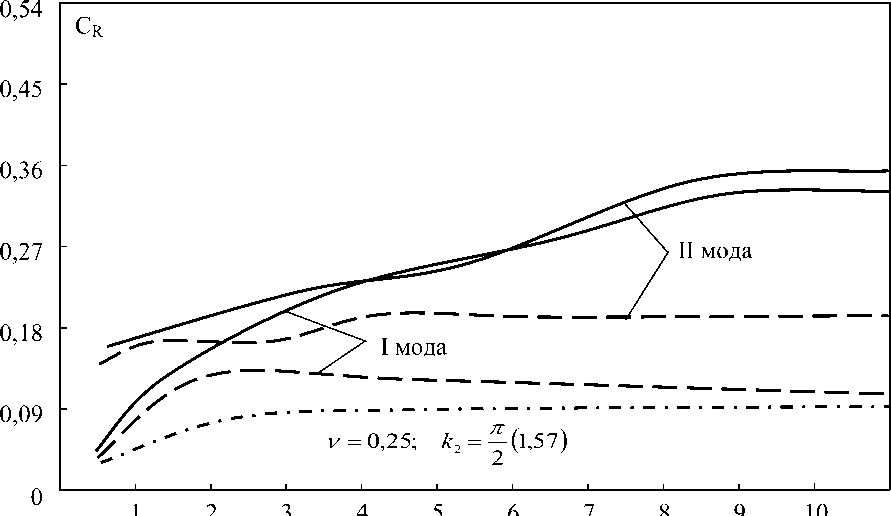
  Рис. 2. Зависимость действительной части скорости (C_R ) распространения волны от волнового числа