Распространение пучков Бесселя и суперпозиций вихревых пучков в атмосфере

Атмосферная лазерная связь в настоящий момент – это бурно развивающаяся отрасль. Системы лазерной связи широко используются при создании локальных сетей для объектов инфраструктуры, находящихся на расстоянии прямой видимости, когда прокладка оптоволоконных кабелей нецелесообразна. Однако дальнейшему развитию этих систем связи мешает стохастичность среды, в которой передаётся сигнал. В атмосфере присутствуют как твёрдые, так и жидкие взвешенные частицы, движения потоков воздуха, тепловой градиент.

В связи с этим в последние годы появляется большое количество публикаций, в которых анализируется прохождение когерентного и частично когерентного света через атмосферу с турбулентностью, пылью, аэрозольными загрязнениями [1–29, 31–40]. При этом модели строились как для простейших лазерных пучков [22, 31–34], так и для более сложных пучков, обладающих орбитальным угловым моментом [1–24, 35, 36]. Подавляющее большинство таких работ являются теоретическими исследованиями на основе математических моделей разных типов [1–25, 31–36]. Теоретические аспекты распространения пучков Бесселя исследованы очень подробно. Так, в [1] исследуется влияние спектральных ограничений на распространение пучков Бесселя в среде с неколмогоровской моделью турбулентности. В [2, 4, 10] исследуются когерентные свойства пучков Бесселя. В работах [3, 6] вводится так называемый обобщённый пучок Бесселя–Лагерра–Гаусса и исследуется приближённая формула средней осевой интенсивности при его распространении через турбулентную атмосферу. В [5] исследуется использование мультиплексирования на основе орбитального углового момента для увеличения пропускной способности передачи данных в свободном пространстве на движущиеся платформы. В [7] теоретически и экспериментально доказывается, что пучки Бесселя высоких порядков более устойчивы к тепловым возмущениям в атмосфере. Эксперимент проводился на оптическом столе, часть оптического пути пучка проходила над нагретой пластиной. В [8, 14] исследовалось влияние анизотропии в модели неколмогоровской турбулентности морской атмосферы. В [9] оцениваются усреднённая по апертуре сцинтилляция, среднее отношение сигнал/шум и средняя частота битовых ошибок как для обычных вихревых пучков, так и для пучков Бесселя, распространяющихся в турбулентной атмосфере. Показано, что по сравнению с обычными вихревыми пучками пучки Бесселя имеют меньшую усреднённую сцинтилляцию. В [11] исследовано влияние сильной турбулентности на состояния орбитального углового момента при распространении инфракрасных бездифракционных пучков в атмосфере. В [12] показано, что среднее значение орбитального углового момента вихревого пучка Бесселя–Гаусса остаётся постоянным при распространении в турбулентной атмосфере.

В работах [15–25] рассматриваются разные модели искажений и разные типы пучков Бесселя, но все эти работы носят теоретический характер. Экспериментальных работ намного меньше, и большинство из них описывают эксперименты на лабораторном столе.

Связано это с техническими трудностями проведения экспериментальных исследований за пределами лаборатории. Тем не менее, есть ряд экспериментальных работ [5, 26–28, 39–42]. Экспериментальные исследования этого направления можно разделить на несколько разных типов: это эксперименты, в которых по искажениям лазерного пучка определяли свойства атмосферы [37, 38], исследования по влиянию турбулентности на качество изображения в оптической системе [39] и исследования устойчивости разных типов пучков к атмосферным неоднородностям [15]. Есть работы по имитации передачи данных с высокой скоростью через турбулентную атмосферу [27]. Однако полностью отсутствуют эксперименты по использованию пучков Бесселя в открытой атмосфере. Единственный приведённый в этом обзоре пример экспериментальной работы в открытой атмосфере – это [5], где используются обычные вихревые пучки для увеличения скорости передачи информации.

Такой явный перекос количества публикаций в сторону теоретического анализа и мелкомасштабных экспериментов не является случайным, что и будет показано в этой работе.

Свойство пучков Бесселя восстанавливаться после прохождения препятствия, которое закрывает часть пучка [29], известно давно. Это свойство будет, безусловно, полезным при использовании этих пучков в системах атмосферной связи. В настоящей работе предпринята попытка проведения эксперимента с пучками Бесселя, а также с суперпозицией обычных вихревых пучков в масштабах, близких к масштабам реальных систем оптической атмосферной связи. Для этого было проведено экспериментальное исследование прохождения пучков Бесселя через участок атмосферы с искусственно созданным потоком теплого воздуха, а также с искусственно созданными аэрозольными преградами.

1.    Эксперимент с пучками Бесселя

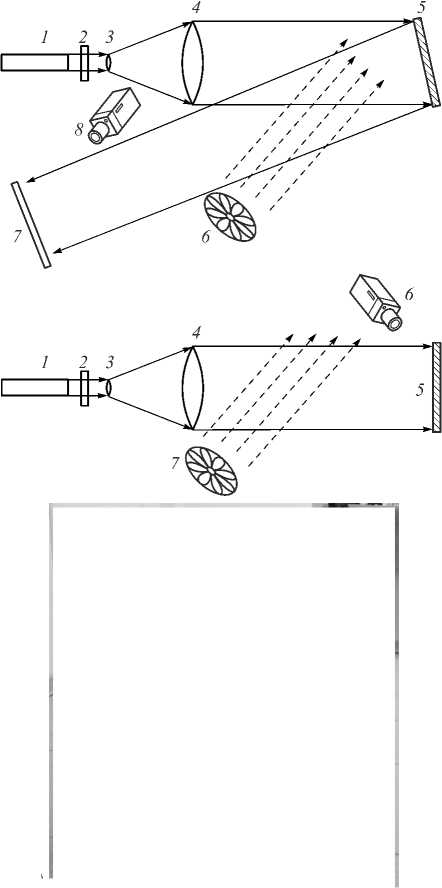
Эксперимент проводился в двух разных конфигурациях. Схема первой конфигурации приведена на рис. 1а. Этот эксперимент проводился в длинном коридоре, где сбоку от места прохождения лазерного пучка устанавливался тепловентилятор с диаметром винта 180 мм, который направлял поток горячего воздуха под небольшим углом к направлению распространения света. За счёт зеркала путь, который проходил световой пучок, удваивался. Общая длина пути составляла 40 м. Вторая конфигурация эксперимента (рис. 1б) была использована уже на открытой местности, и общее расстояние от коллиматора до экрана, на который проецировался пучок Бесселя, составило 110 м. Коллиматор в обеих оптических схемах расширял пучок Бесселя до диаметра центрального самого яркого кольца 50 мм, с общим диаметром 250 мм, что позволяло ему сохранять свою структуру на больших дистанциях. Такой диаметр пучка подбирался, исходя из соотношения для максимального расстояния распространения пучка Бесселя с ограниченной апертурой zmax = Rk/α, где R – радиус вихревого аксикона, α -параметр функции Бесселя, k – волновое число. Для используемого аксикона α =25, k рассчитывалось для длины волны 532 нм. В результате расчёта получилось, что для формирования пучка Бесселя, который бы сохранялся на расстоянии 110 м, необходим мини- мальный размер апертуры около 230 мм. Этот расчёт сразу показывает причину, по которой до сих пор не проводились полномасштабные эксперименты с пучками Бесселя в атмосфере. Для более больших расстояний потребуется апертура пучка, пропорциональная расстоянию. Если пытаться передавать пучок Бесселя на 1 км, диаметр апертуры должен быть уже около 2,5 м. Есть, конечно, возможность уменьшения параметра α, но в этом случае получается пучок Бесселя с малым количеством колец, что приводит к тому, что пучок теряет все свои замечательные свойства.

а)

б)

в)

Рис. 1. Оптическая схема эксперимента по прохождению пучка Бесселя через атмосферу в помещении (а) (1 – лазер, 2 – ДОЭ, 3, 4 – коллиматор, 5 – зеркало, 6 – тепловентилятор, 7 – матовый экран, 8 – видеокамера), оптическая схема эксперимента по прохождению пучка Бесселя через атмосферу за пределами помещения (б) (1 – лазер MGL-III-532, 2 – ДОЭ, 3,4 – коллиматор, 5 – матовый экран), фотография экспериментальной установки (в)

Для формирования пучков Бесселя был использован линейно кодированный вихревой аксикон, рельеф которого представлен на рис. 2. На рис. 2а представлено изображение микрорельефа под оптическим микроскопом, на рис. 2б – трёхмерная реконструкция центральной части микрорельефа дифракционного оптического элемента, полученная на интерферометре белого света NewView 5000.

Рис. 2. Центральная часть микрорельефа ДОЭ,

б)

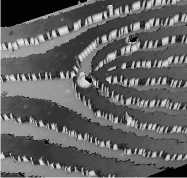
используемая в эксперименте: изображение, полученное на оптическом микроскопе (а), реконструкция на интерферометре белого света New View 7000 (б)

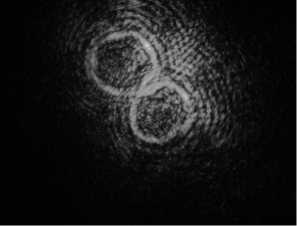
В эксперименте, который проводился в помещении, поток тёплого воздуха подавался на траекторию пучка возле оборотного зеркала. Регистрация распределения интенсивности проходила с матового белого экрана, поскольку из-за размера пучка и отсутствия второй линзы с апертурой 250 мм не хватало размера светочувствительной матрицы. В первом эксперименте не экранировали –1 порядок дифракции, поэтому рядом были сформированы два одинаковых пучка Бесселя. Эксперимент проводился в безветренную погоду при температуре воздуха 27–28°С. Поток тёплого воздуха при малой мощности создавал на оси пучка область с температурой 40–55°С, при большой мощности температура в этой области достигала 47–65°С. На рис. 3 а представлен вид распределения интенсивности при отсутствии потока тёплого воздуха (а), на рис. 3 б – при слабом потоке тёплого воздуха (мощность подогрева 1000 Вт), на рис. 3 в – при сильном потоке (мощность подогрева 2000 Вт).

Представленный на рис. 2 элемент формирует в 1-м порядке дифракции пучок Бесселя 5-го порядка.

б)

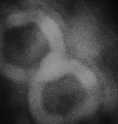
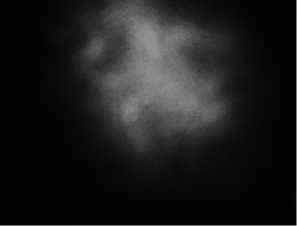
Рис. 3. Распределение интенсивности в двух распространяющихся рядом пучках Бесселя 5-го порядка при отсутствии потока тёплого воздуха (а), при слабом потоке тёплого воздуха (б) (мощность подогрева 1000 Вт), при сильном потоке (в) (мощность подогрева 2000 Вт)

Из рис. 3 хорошо видно, что уже слабый тепловой поток вносит сильные искажения в распределение интенсивности. При сильном тепловом потоке искажения настолько велики, что пучок невозможно идентифицировать как пучок Бесселя. При наличии после области искажений в атмосфере длинного участка спокойного воздуха ситуация меняется. Для этого был проведён эксперимент, в котором на пучок Бесселя действовал точно такой же поток тёплого воздуха, но регистрация распределения интенсивности осуществлялась на расстоянии 110 метров от источника искажений. На рис. 4а представлено распределение интенсивности в центральной части пучка Бесселя на расстоянии 110 м от коллиматора при отсутствии теплового потока, на рис. 4б – при слабом тепловом потоке (1000 Вт), на рис. 4в – при сильном тепловом потоке (2000 Вт).

в)

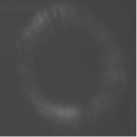
Рис. 4. Распределение интенсивности в центральной части пучка Бесселя на расстоянии 110 м от коллиматора при отсутствии теплового потока (а), при слабом тепловом потоке (1000 Вт) (б), при сильном тепловом потоке (2000 Вт) (в)

Как видно из рис. 4, наличие длинного отрезка относительно спокойного воздуха приводит к тому, что пучок Бесселя, исказившийся до неузнаваемости, всё же восстанавливает свою структуру.

Визуально определить качество пучков на рис. 4 невозможно, поэтому для объективного анализа влияния атмосферных искажений на пучок был использован сцинтилляционный индекс

I ²

ⁿ=- 1, (1)

где средние значения интенсивностей и квадратов интенсивностей считаются по последовательности изображений пучка для каждого пиксела. Чтобы исключить из расчёта сцинтилляционного индекса колебания фона, расчёт вёлся только по тем областям изображений, где интенсивность превышает среднее значение по растру. Для каждого искажающего воздействия снималась последовательность из пяти изображений, по которым и вычислялся сцинтилляционный индекс. При отсутствии теплового потока η=0,0049, при включении потока горячего воздуха мощностью 1000 Вт η=0,0055, при включении потока горячего воздуха мощностью 2000 Вт η=0,0067. В качестве эталона использовался Гауссов пучок, расширенный до этой же апертуры. Для него соответствующие значения составили η=0,0046, η=0,0061, η=0,0074. Видно, что при наличии тепловых потоков искажение Гауссова пучка выше, чем у пучка Бесселя.

Таким образом экспериментально удалось доказать более высокую устойчивость пучков Бесселя к сильным искажениям в атмосфере по сравнению с Гауссовыми пучками, но необходимым условием для этого является наличие достаточно длинного участка спокойной атмосферы.

Расчёты, проведённые выше, показывают необходимость использования больших по апертуре линз для коллимации пучков Бесселя. Очевидно, что практическое применение пучков Бесселя в системах атмосферной связи на больших дистанциях принципиально невозможно.

2.    Эксперимент с суперпозициями вихревых пучков

В [30] описаны вихревые аксиконы, которые позволяют формировать комбинации из нескольких оптических вихревых пучков. При этом получаются пучки с некольцевым распределением интенсивности. Поскольку формирование этих пучков осуществляется аксиконами, то следует ожидать, что эти пучки также будут устойчивы к фазовым искажениям. Для работы были выбраны два вихревых аксикона, которые фор- мируют вихревые пучки с простым и хорошо визуаль- но определяемым распределением интенсивности.

На рис. 5 а приведена фазовая функция такого вихревого аксикона, который формирует вихревой пучок с топологическими зарядами 2 и 4. Формируемое распределение интенсивности представлено на рис. 5 б.

б)

Рис. 5. Фазовая функция вихревого аксикона для формирования вихревого пучка с топологическими зарядами 2 и 4 (а), формируемое распределение интенсивности (б)

Для эксперимента была использована оптическая схема на рис. 1б. Так как необходимости расширять пучок до апертуры 250 мм не было, пучок расширялся коллиматором до размера 50 мм. На рис. 6 представлены экспериментально полученные изображения пучка при разном уровне атмосферных искажений.

По результатам измерения сцинтилляционного индекса получились следующие значения: для движущегося воздуха η=0,0054, для мощности 1000 Вт η=0,0061, для мощности 2000 Вт η=0,0083. На первый взгляд результаты получились хуже, чем для Гауссового пучка. Однако, надо учитывать, что Гауссов пучок в предыдущем эксперименте формировался в апертуре 250 мм. После повторения этого эксперимента с апертурой 50 мм соответствующие значения сцинтилляционного индекса для Гауссового пучка составили для движущегося воздуха η = 0,0051, для мощности 1000 Вт η = 0,0064, для мощности 2000 Вт η=0,0087, что показывает лучшую сохранность со- ставного вихревого пучка.

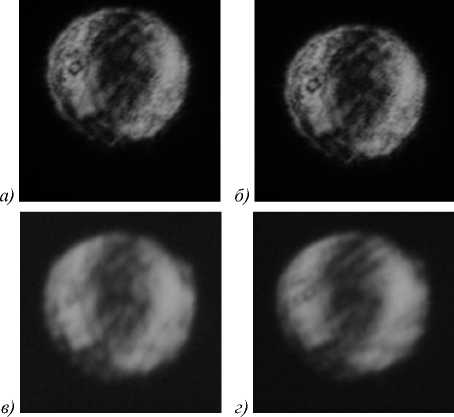
Рис. 6. Распределение интенсивности вихревого пучка с топологическими зарядами 2 и 4 на расстоянии 40 м с неподвижным воздухом (а), при наличии воздушных потоков (б), при наличии потока тёплого воздуха мощностью 1000 Вт (в), при наличии потока тёплого воздуха мощностью 2000 Вт (г)

В экспериментах был использован ещё один вихревой аксикон (рис. 7 а ), который формирует вихревой пучок топологическими зарядами 5 и 8. На рис. 7 б представлено распределение интенсивности

а)

в таком пучке.

б)

Рис. 7. Фазовая функция вихревого аксикона для формирования вихревого пучка с топологическими зарядами 5 и 8 (а), формируемое распределение интенсивности (б)

Для эксперимента была использована оптическая схема на рис. 1б.

На рис. 8 представлены экспериментально полученные изображения пучка при разном уровне атмосферных искажений.

По результатам измерения сцинтилляционного индекса получились следующие значения: для движущегося воздуха η=0,0042, для мощности 1000 Вт η = 0,0065, для мощности 2000 Вт η = 0,0076. Результаты получились лучше, чем для Гауссового пучка такого же масштаба.

Для пучков этого типа было также изучено влияние аэрозолей на устойчивость их распространения. В оптическую схему вместо тепловентилятора монтировалась установка для генерации аэрозолей, которая заполняла аэрозольным облаком часть оптической траектории (около 4 м). Установка показана на рис. 9.

б)

г)

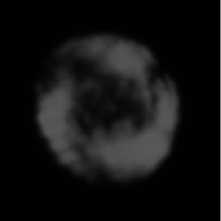
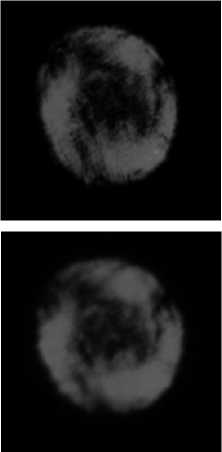
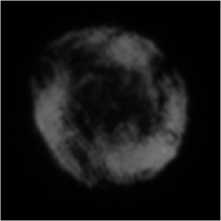
Рис. 8. Распределение интенсивности вихревого пучка с топологическими зарядами 5 и 8 на расстоянии 40 м с неподвижным воздухом (а), при наличии воздушных потоков (б), при наличии потока тёплого воздуха мощностью 1000 Вт (в), при наличии потока тёплого воздуха мощностью 2000 Вт (г)

Поскольку сделать непосредственное измерение концентрации аэрозольных частиц в воздухе не представлялось возможным, контроль этой концентрации осуществлялся по косвенным параметрам. Известна производительность установки по массе использованной жидкости и средний размер генерируемых аэрозольных частиц, а также объём заполняемой части оптической траектории. Примерную концентрацию частиц аэрозоля можно задать, контролируя время генерации. Используемая установка переводит в аэрозольное состояние 24 г жидкости в минуту, средний размер частиц – 15 мкм. Таким образом, каждые 5 с генерации создают концентрацию аэрозольных частиц примерно 4,2×105 м–3. Последующие эксперименты проводились с генерацией аэрозоля в течение 5 с, 10 с и 15 с соответственно. На рис. 10 представлены распределения интенсивности.

В табл. 1 приведены данные по значению сцинтилляционного индекса для каждой концентрации аэрозольных частиц для каждого пучка.

Табл. 1 Данные по значению сцинтилляционного индекса для каждой концентрации аэрозольных частиц

Концентрация частиц м –3	Пучок с топологическими зарядами 2 и 4	Пучок с топологическими зарядами 5 и 8
4,2×105 м-3	0,0058	0,0054
8,4×105 м-3	0,0079	0,0061
1,2×106 м-3	0,0097	0,0072

Как видно из табл. 1, пучок с более высокими значениями топологических зарядов в суперпозиции более устойчив к аэрозольному туману.

Заключение

Проведённый эксперимент наглядно показал, что пучки Бесселя действительно могут восстанавливать свою структуру не только после экранирования части пучка, но и в случае фазовых искажений по всему диаметру пучка. На малых дистанциях фазовые иска- жения меняют распределение пучка так, что он становится неидентифицируемым как пучок Бесселя. При наличии достаточно продолжительного участка спокойного воздуха пучок Бесселя восстанавливается. Приведённые в статье расчёты показывают, что пучки Бесселя вряд ли могут быть использованы в системах связи на дистанциях более 100 м, что, по всей видимости, и обуславливает отсутствие крупномасштабных экспериментальных работ.

Рис. 9. Внешний вид установки для генерации аэрозоля во время работы

а)

б)

в)

г)

д)

е)

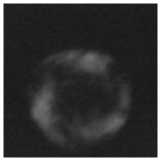
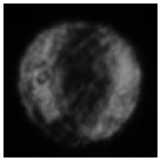
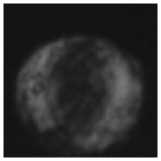
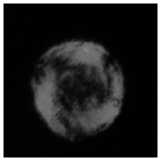
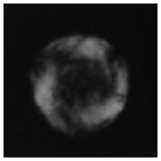
Рис. 10. Распределение интенсивности вихревого пучка с топологическими зарядами 2 и 4 на расстоянии 40 м с концентрацией аэрозольных частиц 4,2×105 м–3 (а), с концентрацией аэрозольных частиц 8,4×105 м–3 (б), с концентрацией аэрозольных частиц 1,2×106 м–3 (в), распределение интенсивности вихревого пучка с топологическими зарядами 5 и 8 на расстоянии 40 м с концентрацией аэрозольных частиц 4,2×105 м–3 (г), с концентрацией аэрозольных частиц 8,4×105 м–3 (д), с концентрацией аэрозольных частиц 1,2×106 м–3 (е)

Суперпозиции вихревых пучков, генерируемых вихревыми аксиконами, не имеют существенных ограничений по апертуре, но по результатам экспериментов практически также устойчивы к атмосферным искажениям, как и пучки Бесселя. Так, предельное значение сцинтилляционного индекса для пучка Бесселя 5-го порядка составило 0,0074, при тех же самых условиях для суперпозиции вихревых пучков с топологическими зарядами 2 и 4 значение сцинтилляционного индекса составило 0,0083, а для суперпозиции вихревых пучков с топологическими зарядами 5 и 8 – 0,0076. Т.е. результаты во втором случае почти совпадают с результатом для пучка Бесселя.

Работа выполнена при поддержке Министерства образования и науки РФ в рамках госзадания проект № 3.3025.2017/8.9, а также в рамках государственного задания ФНИЦ «Кристаллография и фотоника» РАН (соглашение № 007-ГЗ/Ч3363/26) в части изготовления вихревых аксиконов, а также при поддержке грантов РФФИ №№ 18-29-20045мк, 16-29-11744 офи_м, 16-29-09528 офи_м.