Расширение рабочего пространства технологического оборудования, построенного на основе ротопода

На кафедре «Автоматизация механосборочного производства» Южно-Уральского государственного университета ведутся разработки технологических манипуляционных устройств на основе механизма с параллельными кинематическими цепями типа «ротопод» [1].

На рис. 1 представлена упрощенная кинематическая схема механизма-ротопода, состоящая из подвижной платформы (с полюсом С), соединенной с неподвижным основанием при помощи шести штанг постоянной длины. Сферические шарниры Bi (i = 1...6)

связывают штанги с под-

вижной платформой; кардановые шарниры Ai (i = 1...6) штанг расположены на каретках, кото- рые могут перемещаться по неподвижной круговой направляющей. Угловые координаты центров кардановых шарниров фi (i = 1...6) примем за входные (управляемые) координаты. Выходным звеном ротопода является подвижная платформа.

Конструкция механизма обеспечивает движение детали, закрепленной на подвижной платформе ротопода, по шести независимым координатам: трем линейным и трем угловым. В качест-

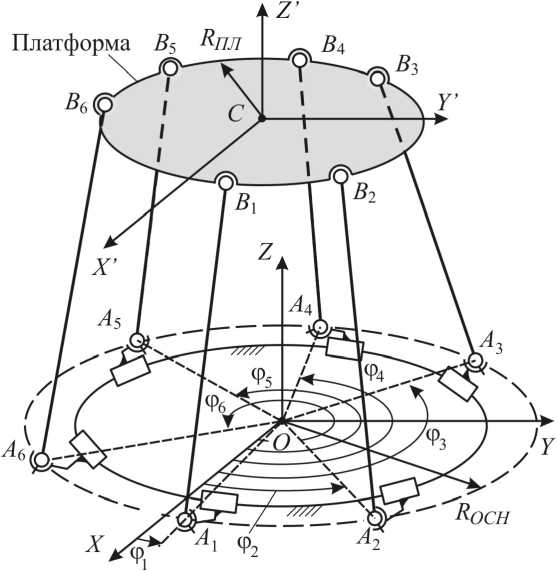
Рис. 1. Кинематическая схема ротопода

ве линейных выступают координаты полюса С платформы в неподвижной системе координат (СК) OXYZ . Угловые координаты определяют разворот подвижной платформы вокруг полюса; в качестве этих координат могут быть использованы, например, три угла Крылова, описывающие разворот связанной с платформой СК CX ' Y ' Z ' относительно неподвижной СК OXYZ . Шесть описанных координат будут являться для рассматриваемого устройства выходными координатами.

В зависимости от выбранного закона изменения входных координат ф i ( i = 1...6 ) можно получить различные траектории движения его выходного звена.

Для технологического оборудования важным параметром является его рабочее пространство, т. е. совокупность точек, в которых может находиться заданная точка рабочего органа этого оборудования. Наличие замкнутых кинематических цепей, связывающих платформу с неподвижным основанием, не только увеличивает жесткость механизма-ротопода, но и уменьшает рабочее пространство оборудования на его основе. Задача расширения рабочего пространства для ротопода является актуальной как при проектировании новой конструкции, так и при анализе существующей. При моделировании рабочего пространства должна решаться обратная задача кинематики о положениях. Эта задача для ротопода решается аналитически [1, 2]: путем нахождения угловых координат фi кардановых шарниров по заданным координатам выходного звена.

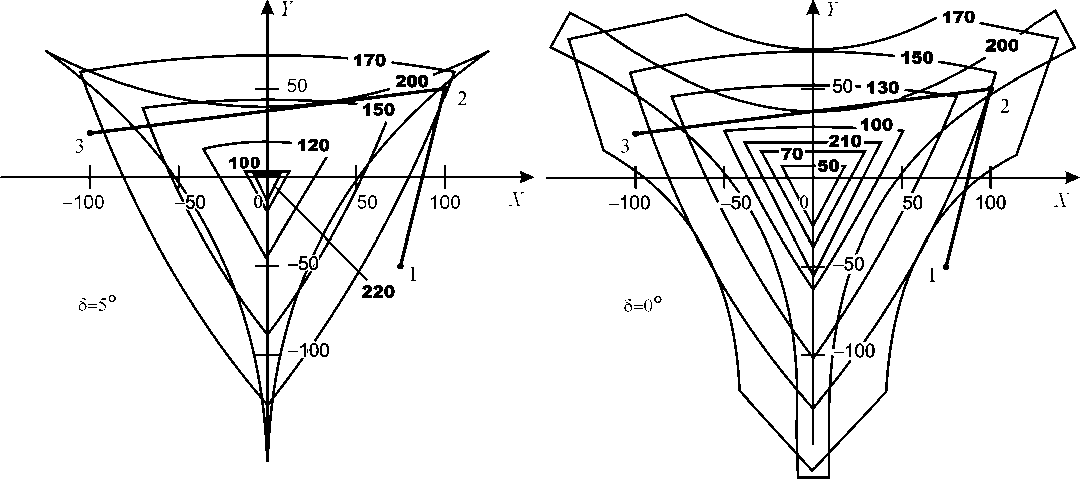
На рис. 2, а показано рабочее пространство реального технологического манипуляционного устройства, созданного при участии авторов. Механизм, положенный в основу конструкции, имеет (см. рис. 1) R qc_H = 320 мм , R ПЛ = 220 мм, A i B i = 245 мм . Расчет рабочего пространства проведен для полюса C подвижной платформы; все ее выходные угловые координаты приняты равными нулю. Рабочее пространство представлено в виде сечений, параллельных плоскости OXY , координаты Z этих сечений заданы в миллиметрах.

а)                                                                      б)

Рис. 2. Рабочие пространства механизмов

Одной из задач при проектировании (модернизации) ротопода может являться максимизация площади одной из плоскостей рабочего пространства с целью увеличения зоны перемещения полюса подвижной платформы. В технологическом манипуляционном устройстве сферические шарниры могут рассматриваться в виде трех пар, в каждой из которых шарниры «разведены» относительно среднего положения на угол 5 (рис. 3). Для случая, показанного на рис. 2, а, 5 = 5 ° . При заданных R _ОСН , R _ПЛ и длине штанг угол δ может использоваться в качестве конструктивного параметра, влияющего на форму рабочего пространства.

Исследование влияния угла δ на размеры сечений рабочего пространства показало, что максимизация площади наблюдается при 5 = 0, т. е. при попарном сведении шарниров. Рабочее пространство ротопода для этого конструктивного случая показано на рис. 2, б.

Пусть для исследуемого механизма нужно обеспечить перемещение полюса подвижной платформы из точки 1 с координатами (75, –50, 170) в точку 2 с координатами (100, 50, 170), затем в точку 3 с координатами (–100, 25, 170); угловые выходные координаты должны оставаться равными нулю. Очевидно, что для механизма с исходным значением 5 = 5 ° (см. рис. 2, а) такое перемещение не осуществимо; для механизма с попарно «сведенными» шарнирами реализуемо только перемещение полюса из точки 2 в точку 3 (см. рис. 2, б).

Реализация попарного «сведения» шарниров в реальной конструкции затруднительна, поэтому рассмотрим иной подход к решению задачи увеличения площади сечения рабочего пространства механизма-ротопода.

В работе [2] показано, что при решении обратной задачи о положениях для ротопода имеет место неоднозначность в определении входных координат ф- ( i = 1...6). Центры кардановых шар-

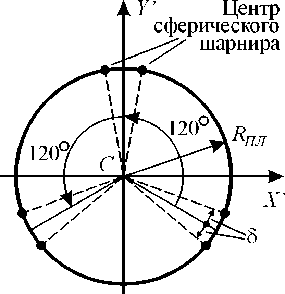
Рис. 3. Угол «разведения» центров сферических шарниров

ниров, положение которых определяется углами φ i , являются общими точками окружности R _ОСН и сферы, радиус которой равен длине штанги механизма (рис. 4, показана часть сферы). Общих точек может быть одна или две, следовательно, для каждой штанги может быть записано одно или два значения угла φ.

Каждое из двух возможных положений i -й штанги определяется знаком угла и i : для положения A 1 этот угол отрицателен, для положения A_i ² – положителен (см. рис. 4). Угол и i отсчитывается от нормали, опущенной из центра сферического шарнира B_i на отрезок, соединяющий точки A_i ¹ и A_i ² возможных положений центра карданового шарнира A_i .

Изменение знака этого угла отражает процесс перехода механизма из одной конфигурации в другую. Граница между конфигурациями - равенство нулю какого-либо из углов и i ( i = 1.. .6 ) . В этом случае сфера и окружность имеют одну общую точку касания.

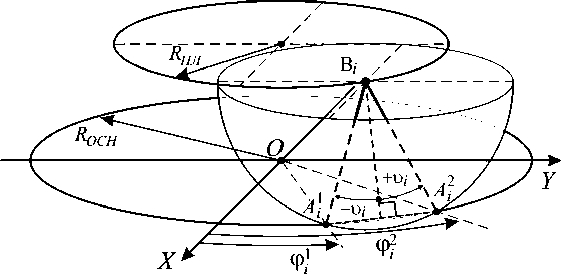
Рис. 4. Возможные положения i -й штанги механизма

Для механизма-ротопода можно выделить 64 различные конфигурации, следовательно, для каждого вектора выходных координат существует 64 вектора входных координат: 111111    111112    111121

A 1 = ( A 1 A 2 A 3 A 4 A 5 A 6 ) ,    A 2 = ( A 1 A 2 A 3 A 4 A 5 A 6 ),     A 3 = ( A 1 A 2 A 3 A 4 A 5 A 6 ),    •"’

A ₆₄ = ( A 1 A 2 A 3 A 4 A ₅ A ₆); для каждой из конфигураций A j можно построить свое рабочее пространство. Так как за счет изменения входных координат механизм-ротопод может переходить из одной конфигурации в другую, то возможно рассмотрение совокупного для нескольких конфигураций рабочего пространства. Рабочее пространство технологического манипуляционного устройства, показанное на рис. 2, а, соответствует конфигурации A 22 = ( A 1 A 2 A₃ A 4 A ₅ A ₆ ). В силу малой величины угла δ и из-за ограничений на соударения кареток получить в этом устройстве другие конфигурации при равенстве нулю выходных угловых координат невозможно. Очевидно, что при попарном сведении сферических шарниров, т. е. при 5 = 0, в ротоподе может быть реализована единственная конфигурация A ₂₂ .

При увеличении угла δ становится возможной реализация конфигураций, отличных от A ₂₂ . В общем случае из набора конфигураций наибольший практический интерес представляют кон- 111222   122211

фигурации, описываемые векторами A 8 = ( A 1 A 2 A 3 A 4 A 5 A ₆), A 29 = ( A 1 A 2 A 3 A 4 A ₅ A ₆), A 221112    121212

50 — (A-1  a.2 A"3 A-4 A-5 a.6 ) и .^a22 — (A-1 a.2 a.3 a.4 A-5 a.6 ) (рис. 5), соответствующие случаям максимальной жесткости.

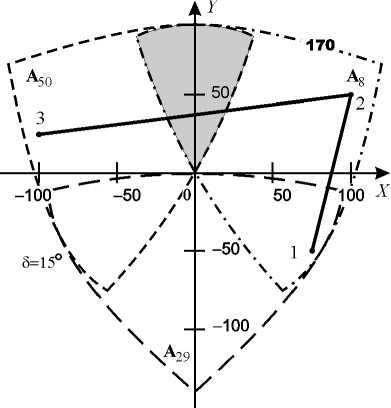
На рис. 6 показано сечение Z = 170 мм совокупного для этих конфигураций рабочего пространства механизма, имеющего 5 = 15 ° . В этом сечении из-за возникновения соударений кареток, на которых расположены кардановые шарниры A_i , реализация конфигурации A ₂₂ при заданных параметрах механизма невозможна.

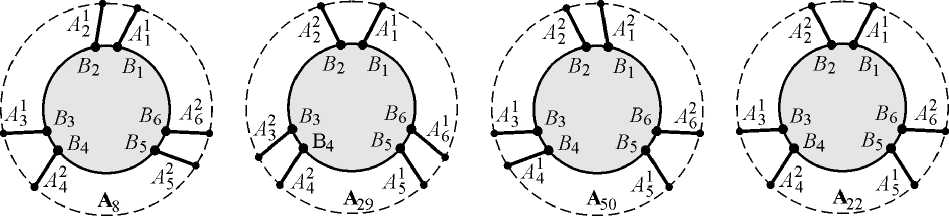
Рис. 5. Конфигурации, обеспечивающие максимальную жесткость механизма

Из сравнения рис. 2, а и рис. 6 видно, что площадь сечения, соответствующего рабочему пространству каждой из конфигураций механизма с 5 = 15 ° , меньше, чем площадь сечения Z = 170 мм рабочего механизма с 5 = 5 ° . Однако суммарная площадь, определяющая область возможных положений полюса C с учетом трех конфигураций механизма с 5 = 15 ° , превосходит площадь сечения рабочего пространства механизма с 5 = 5 ° . В частности, механизм, имеющий 5 = 15 ° , позволяет осуществить перемещение полюса из точки 1 с координатами (75, -50, 170) в точку 2 с координатами (100, 50, 170), затем в точку 3 с координатами (–100, 25, 170). Движение из точки 1 в точку 2 осуществляется при конфигурации A ₈ . Движении из точки 2 в точку 3

должно начинаться при конфигурации A8 , а заканчиваться – при конфигурации A50 . Выделен- ная серым цветом область соответствует зоне наложения рабочих пространств разных конфигу- раций. В некоторой точке, принадлежащей зоне наложения, необходимо осуществить перекон-

фигурирование механизма. В начале и

в конце переконфигурирования платформа механизма должна занимать одно и то же положение. Промежуточные положения, занимаемые платформой при пере-конфигурировании, не должны приводить к ситуациям, не предусмотренным решаемой с использованием механизма технологической задачей. Для обеспечения этого при переконфигурировании могут изменяться все шесть входных координат.

Очевидно, что реализация переконфигурирования не позволяет осуществить непрерывное движение рабочего органа по требуемой траектории.

Рис. 6. Сечение совокупного для трех конфигураций рабочего пространства:

– сечение рабочего пространства для конфигурации A 8 ;

– сечение рабочего пространства для конфигурации A 29 ;

– сечение рабочего пространства для конфигурации A 50

Таким образом, неоднозначность решения обратной задачи о положениях для ротопода может использоваться для расширения рабочего пространства этого механизма. При движении по заданной траектории внутри «расширенного» рабочего пространства может потребоваться осуществить перевод механизма из одной конфигурации в другую.