Разностная схема для решения уравнений роста опухоли с учетом ограничения потока

Постановка задачи

Раковые заболевания являются одной из основных причин смертности в мире. На онкологические исследования ежегодно тратятся значительные средства. К настоящему времени накоплено огромное количество эксперементального материала, о течении раковых заболеваний. Основываясь на анализе этого материала, удалось установить некоторые механизмы, способствующие росту и развитию раковых опухолей. Математическое моделирование, наряду с экспериментом, является важным инструментом для исследования закономерностей опухолевого роста. Существует большое количество разнообразных математических моделей, от простых диффузионных до сложных многоуровненых, которые описывают различные аспекты развития опухолей (рост, васкуляризацию, ангиогенез и др.), а. также позволяют оценить эффективность воздействий на опухоль путем решения задач оптимального управления.

В данной работе предлагается модель с учетом диффузионной и хемотаксической подвижности опухолевых клеток, а. также гетерогенного окружения, основанная на подходе [1]. Существенными недостатками [1] являются возможность роста, суммарной концентрации клеток до любого уровня, а. также бесконечная скорость распространения опухолевых подвижных клеток. Одним из путей решения этих проблем является постановка вариационной задачи, аналогично [2], с учетом ограничений типа неравенств на полный поток и суммарную численность клеток. Другой путь — использование феноменологического ограничения потока подвижных клеток. Такой подход использовался в [3] для моделирования релаксационного теплопереноса в плазме. Здесь он применяется для биологической задачи. С учетом ограничения потока система уравнений в одномерном случае имеет вид:

∂n ∂t

∂

∂x

[(¹ -

c

c max

Д -^ ₊

∂x ∂x

+ P 1 ( S ) m - P 2 ( S ) n - d n n

∂m

∂t

∂l

∂t

^qmS (1 ^- ^

- P 1 ( S ) m + P 2 ( S ) n,

eiS (1 - c) - Hl ( n + m ) ,

∂S ∂t

■ "S

- γ l Sl - γ m Sm - γ n Sn,

где n — концентрация подвижных неделящихся опухолевых клеток, m — концентра ция неподвижных делящихся опухолевых клеток, 1 — концентрация здоровых клеток, S — концентрация питательного субстрата, c ■ n + m + l — суммарная плотность клеток, D — коэффициент диффузии подвижных опухолевых клеток, а — коэффициент хемотаксиса по отношению к субстрату, q — скорость роста неподвижных опухолевых клеток, P 1 ( S ) ■ K ¹ - th ^{( Е} ( S^{- S cr} )) _i P, ( S ) ■ K ¹ - th ^{( Е} ( S cr ^{- S} )) — функции итенсивности перехода из неподвижного состояния в подвижное и обратно.

Суммарная плотность клеток c ■ n + m + 1 не должна превышать максимально возможную плотность для ткани c < c max. При достижении в некоторой области ткани плотной клеточной упаковки, миграция подвижных опухолевых клеток в данную область прекращается. С учетом этого ограничения выражение для полного потока записывается в виде:

Т ■ ( 1 - ) ( -D^n + »S ) . c max ∂x ∂x

С введением такого ограничения на поток нарушается параболический тип уравнения, может иметь место вырождение в гиперболический тип. Как для квазилинейных уравнений параболического типа, так и для уравнений гиперболического типа возможно наличие слабых (обобщенных) решений.

Развитие опухоли в задаче можно трактовать как появление новой фазы. Среди решений рассматриваемой системы в зависимости от параметров задачи возможно как диффузионное распространение подвижных клеток без формирования выраженной границы [4], так и возникновение резкой границы между опухолевыми и здоровыми клетками [5]. Такому характеру роста опухоли может соответствовать обобщенное решение. При достижении максимально возможной клеточной плотности c max появляется условная граница раздела фаз между опухолью с плотной клеточной упаковкой и ее окружением.

В основном, математическое описание процессов переноса с фазовыми переходами строится на основе задачи Стефана. Классическая задача Стефана предполагает, что фазовый переход локализован в узкой области фронта, который является поверхностью слабого разрыва для функции температуры. Положение фронта фазового перехода меняется со временем и ищется в процессе решения задачи. Задача Стефана послужила основой для большого числа обобщений. Данная задача также сводится к обобщенной (нелинейной) задаче Стефана.

Пусть в системе при достижении суммарной плотности клеток максимально возможного значения возникла поверхность разрыва фаз (рис. 1). Рассмотрим движение

Л.С. Исаченко, А.И. Лобанов этой границы. Ее положение можно описать функцией £ (t). Найдем скорость движения границы. Предположим без ограничения общности, что она движется слева направо. Пусть в момент времени t граница находится в £ (t), за некоторое малое время At она переместится в точку £ (t + At) 11 пройдет расстояние VAt. где V — скорость подвижной границы. Так как время At мало, скорость V можно считать постоянной.

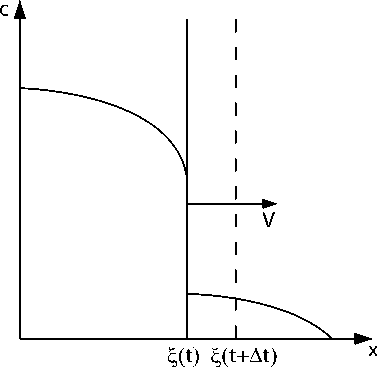
Рис. 1. К оценке фазовой скорости границы

Просуммировав (1) - (3), получим уравнение баланса для суммарной плотности клеток д! = —д [(1 — С) (+ anddS)] + g,                 (5)

∂t ∂x            ∂x ∂x гле g = qmS (1 — c/k) + eiS (1 — c/k) — Hl (n + m) — dnn.

Интегрируем уравнение баланса (5):

t +д t

∂c

J dtdt = —

t +д t

/ Wt +

∂x

t

t +д t

I gdt =

t

-

V

§ ( t +д t )

/

§ ( t )

∂W

,, dx + ∂x

t+д t gdt.

t

Тогда за время At баланс клеток в области, через которую проходит граница раздела фаз, можно записать c (t + At) — c (t) = — V (W(£ (t + At)) — W(£ (t))) + (g (t + At) — g (t)) At.

Считая, что при малых значениях At значение потока W(£ (t)) соответствует потоку слева от границы, a W(£ (t + At)) — справа, получим выражение для скорости границы r= IW

Ig ] at — | c] ’ где |W] — скачок полного потока, |c] — скачок суммарной концентрации клеток на границе. |g] — скачок функции g.

Также, исходя из балансовых соотношений, получим условие на разрыве для по тока

W

1 — с

= 0 .

Полагается, что изначально небольшое количество опухолевых клеток находится в центре расчетной обасти L. Граничные условия имеют вид:

П х (0 ,t ) = 0 , m x (0 ,t ) = 0 , l x (0 ,t ) = 0 , S x (0 ,t ) = 0 ,

n x ( L,t ) = 0 , m x ( L, t ) = 0 , l x ( L, t ) = 0 , S ( L,t ) = 1 .

При решении задачи Стефана существенно повышаются требования к численному методу. При численном построении слабого решения необходимым свойством является консервативность разностной схемы.

1.    Разностная схема

Для решения задачи Стефана используются численные методы без явного выделения раздела фаз, т.е. однородные разностые схемы [6], и методы, явно выделяющие подвижную границу и учитывающие ее движение [7]. Для исследования свойств данной одномерной задачи будем использовать разностную схему с явным выделением разрыва.

Система уравнений приводится к безразмерному виду. В области решения вводится равномерная по пространству расчетная сетка, выбор шага по времени при послойном переходе осуществляется автоматически. Используется двухслойная неявная разностная схема. Для значений на верхнем слое используются обозначения с -D». Для построения консервативной разностной схемы необходимо пользоваться дивергентной формой записи уравнений. С этой целью преобразуем выражение — ddx [(1 — с ) ( —D 1П + andx^], воспользовавшись аппроксимацией Шарфеттера [8]. Получим

∂              ∂n ∂n ∂             αS ∂ αS

• ^{—    (1 —} c ) ^—D   + ^an     =    ^{(1 —} c ) De D — (ne d .

∂x            ∂x ∂x ∂x            ∂x

Разностное уравнение для подвижных опухолевых клеток имеет вид

ˆˆ

„   n ₊₁ e - d ^{S +1} — ne - d S

κ ₊ 1 _{2           h}

-

/X

κ _-

αˆ ne D S

-     - a S

—]⁺ f ( n -m,S )

— dn,

/X где к+2   =

^{(1 —} c + ^{1 —} C₊ 1 )

Kqn

1 -th ( Scr-S)

αˆ αˆ eDSeDS+1

z.                          z-          a

αα e d S + e d S+1

f n n , m n , S ⁿ

Kqrh

1 -th ( S-Scr )

-

Значения величин на n — 1 и

n + 1 шагах по пространству обозна

чаются индексами - 1 и ₊₁.

Для субстрата, здоровых и неподвижных опухолевых клеток разностные уравнения записываются очевидным образом

/X

S-S

τ

D

= Д 2 ( S +1 — ² S + S - 1) — Y з Sn — Y 2 Sm — y 1 Shi e ,

Л.С. Исаченко, А.И. Лобанов

/X l

-l

τ

вЧ1 -1)

/X

- Hl ( n + m ) ,

m-m

τ

qimS (1 - ^ - f ( n, mi, S ) .

Модифицируем разностные уравнения вблизи подвижной границы. Рассмотрим случай, когда граница движется слева направо. Для аппроксимации функции ф ( t ) используется кусочно-линейная экстраполяция

/X

( = ( + Vt, где V — скорость границы на нижнем слое.

Так как в ф разрыв, запишем производные по пространству с использованием дополнительной точки ф Обозначим значения величин справа от разрыва индексом ф ₊ , слева — индексом ф - . Тогда слева от границы разностное уравнение для подвижных опухолевых клеток имеет вид

n

-

n

2 D

(1 - с + 1

-

τ

/X

Ф - X n + h

А

ξ - x _n

с- n^

-

n e D ⁽ Sc

^S )

-

/X

α

1 + e ^D

(д

S )

)

-

2 D

(1 - с +1

-

-1 1 )

Ф ^- x n ⁺ h

h

(

ne D ^{( S}— i ^{- S} )

-

ⁿ - 1

α

1 + e ^D

( S - 1 -S )

)

+ f (n ,im,

S

-

d n n.

Справа от границы

n

-

n

2 D

(1 - с +1

-

τ

/X

-

x n

-

ф + h

2 D

/X

h

c +1 ) ^+1

^{(1 -} c ^{+ 1 -} C £ + )

-

ne D ^{( S} +i ^{- S} )

α

1 + e ^D

( ^S +1

s )

)

-

x n

-

Ф + h

x n

-

/X

ξ

(

n e D ⁽ Sc+^{- S} )

-

n +

1 + e D ( ^S c + -S )

)

+ f nn /im,

S

-

d n n.

Для того чтобы получить однородную схему, из разностных уравнений необходимо исключить n ^- и n ₊. Используем для этого соотношения на разрыве (6), (7).

В итоге слева от границы:

n-n

2 D      (1 - с +1 - с +1 )

( n ₊₁ - n e ^{D ( S +1 S}

e -D ( S +i -S ) (xn+h — l

τ

-

Ф - X n + h Л+ _e D ( s+i-S ) ( — n) A             h ⁺ V ^{( c - c} +i )

2D      (1 - с + 1 - с+1)         Адт ф - Xn + h (1 + eD(S+i-S)(-n)) (h + D (1 - с+1))

2 D (1 - с + 1 - с - 1 )

+ "1          7     ”77 TV ф - xn + h (1 + eD (S-1-S))

ne D ^{( S - 1 S )} - n - A ( _  )

-------h------- I + f n,m,S) - dnn гДе Аg = elS (1 - k) + qmS (1 - k) - dnn - el+1S+1 ^1--k" j - qm+1S+1 ^1--k" j + dnn+1-

Справа:

n — n 2 D —

^T £ - x n + h

(1 - ^C + 1 - C +1 )

a (e     e\ ⁽ 5-xn )

1 + _e D ^{( S} +1 ^{- S})-- h—

+

2 D

£ - x n + h

⁽¹ - ^c + ¹ - C +1 )

( 1+ e D ( S +i -S ) - A?¹)

(n ,₊i — ne D ( S +i -S )) e -D ( S +i -S l x +H h + D ^{( c — c} +1 )

А дт       ,

( h + D ⁽ c^{— C} +i ))

2 D h - xn + h

(1 — c + 1 — C - 1 )

(1+

e D ( S

1 ^-

A

S

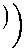
ne D ^{( S 1 S )} - n - 1        (А л -

-------h ------- I + f n,m,Sj — d n n

Полученная система нелинейных сеточных уравнений решается методом квазилинеаризации. Для линеаризованной системы уравнений используется метод матричной прогонки.

2.    Результаты расчетов

В зависимости от параметров задачи, получено три различных типа профилей плотности опухолевых клеток. На рис. 2 приведен результат расчета, когда подвижных границ не возникает и наблюдается диффузионный рост опухоли.

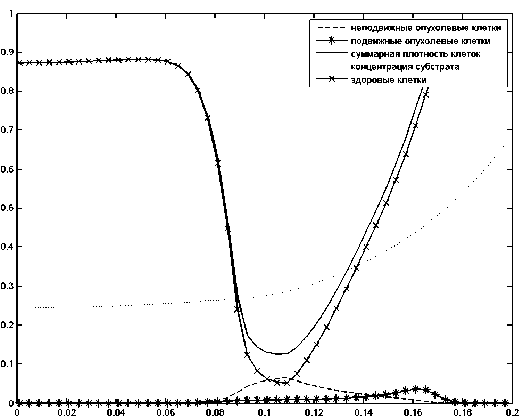
Рис. 2. Плотность клеток и концентрация субстрата при отсуствии подвижных границ. Значения параметров D — 0 , 026, а — 0 , 2, q — 100

На рис. 3 представлено распределение плотности клеток при возникновении подвижных границ, но при отсуствии вырождения в гиперболический тип. На рис. 3 хорошо видно влияние субстратного таксиса на скорость движения границ. При движении против субстратного таксиса граница начинает в итоге размываться.

На рис. 4 представлено распределение клеток при возникновении подвижных границ и вырождении уравнения в гиперболический тип. В данном случае появляется несколько границ разделов фаз.

Л.С. Исаченко, А.И. Лобанов

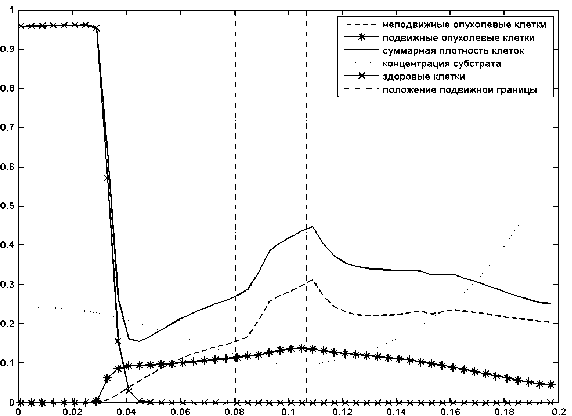
Рис. 3. Плотность опухолевых клеток и распределение субстрата при наличии подвижных границ (отсуствует вырождение в гиперболический тип уравнения). Значе ния параметров D = 0 , 026. а = 2. q = 100

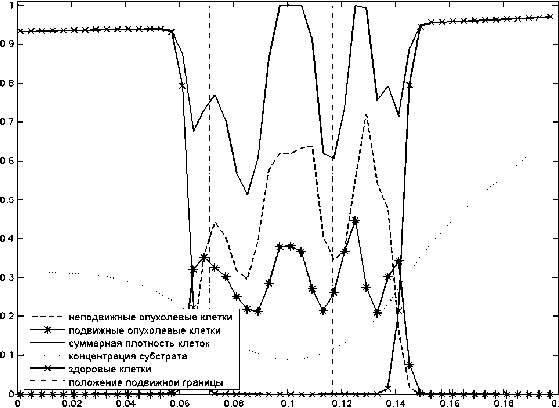
Рис. 4. Плотность опухолевых клеток и распределение при наличии подвижных границ (вырождение в гиперболический тип уравнения). Значения параметров D = 0 , 026. а = 2. q = 150

Заключение

Для решения одномерной задачи роста опухоли с учетом ограничения потока подвижных клеток на базе обобщенной задачи Стефана построена и реализована разностная схема с явным выделением разрыва. Тестовые расчеты показывают, что предложенная разностная схема является эффективной для решения поставленной задачи и позволяет получить три различных профиля решения при расчете по однородной разностной схеме.