Разработка и возможности применения алгоритма вычисления энтропии звуковой волны

Задача идентификации человека по голосу находит все более широкое применение, в частности, в системах разграничения доступа к физическим объектам и информационным ресурсам, в робототехнике, в системах голосового управления, в криминалистике, банковских и телекоммуникационных системах и других областях.

Однако несмотря на широкий спектр применения и достоинства голосовой идентификации, при решении данной задачи возникает множество проблем, связанных с воздействием внешней среды: наличие акустических шумов, аппаратных помех, зависимость от характеристик записывающих устройств [3]. Существует ряд проблем, связанных с тем,

что голос человека – не статичен, он меняется в зависимости от настроения, возраста, наличия каких-либо естественных причин, кроме того, человек может сознательно изменять громкость, высоту и другие параметры голоса.

В частности, задача определения эмоционального состояния говорящего также достаточно актуальна [2]. Ее решение может применяться как совместно с решением задачи голосовой идентификации, в качестве дополнения, так и в других областях, например в системах телекоммуникаций при работе с клиентами.

Актуальность данного исследования заключается в том, что предпринимается попытка найти принципиально новый метод установления свойств голоса человека (его принадлежность к личности и определение эмоций), использующий интегральную характеристику звуковой волны – энтропию.

Вычисление энтропии звука

В теории информации энтропия является мерой неопределенности источника сообщений и определяется как математическое ожидание количества информации в отдельных элементарных сообщениях [5]:

n

H =- Ё Pi *log( Pi ),            (1)

i = 0

где p i – вероятность появления i -го элементарного сообщения.

Для вычисления энтропии звуковой волны была введена интегральная характеристика – энтропия функции, которая вычисляется следующим образом (рис. 1): исходная функция преобразуется в дискретный сигнал, определяются максимальное и минимальное значения на заданном отрезке.

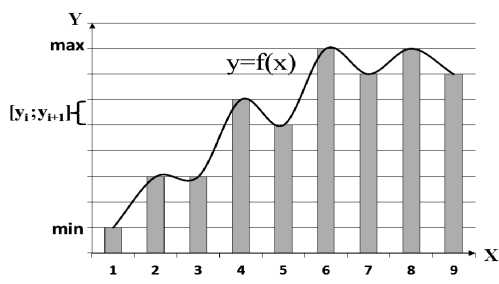
Рис. 1. Вычисление энтропии функции

Затем отрезок [min; max] на оси ординат разбивается на n равных шагов (отрезков [ y i , y i +1]), каждый из которых рассматривается как элементарное сообщение источника. Тогда для каждого элементарного сообщения можно вычислить количество значений сигнала, принадлежащих ему, а, следовательно, и его вероятность, тогда энтропия функции на заданном отрезке вычислится по формуле (1).

Для звуковой волны голоса человека разделение оси ординат по минимуму и максимуму на n равных частей будет сильно менять значение энтропии, в случае, если минимум или максимум оказался нетипичным проявлением голоса, редким значением, сильно отличающемся от всех остальных. Это приводит к "растяжению" шага по оси ординат и к резкому уменьшению энтропии.

Для того чтобы избежать подобной ситуации, был реализован алгоритм вычисления энтропии фрагмента голосового сообщения по средним значениям минимума и максимума:

• а) . Строится огибающая минимумов и максимумов функции, и вычисляются средние значения минимума min s и максимума max s сигнала;

• b) . Отрезок [min s ; max s ] разбивается на n равных частей, каждая из которых является элементарным сообщением;

• c) . Множество элементарных сообщений дополняется необходимым количеством отрезков k оси Y так, чтобы значения min и max входили в крайние отрезки, тогда общее количество элементарных сообщений равно n+k ;

• d) . Определяется принадлежность каждого значения дискретного сигнала к одному из отрезков по оси Y;

• e) . Вычисляется энтропия по формуле (1).

Разработанный алгоритм обладает рядом достоинств, что позволяет применять его для решения различных задач. Во-первых, данный алгоритм получает результат, который не зависит от громкости записи. Данный факт имеет большое значение, так как позволяет избежать зависимости от громкости записи различных устройств (как известно, разные микрофоны могут иметь разную громкость записи). Также применение данного алгоритма позволяет избежать сильных погрешностей, которые могут возникнуть из-за влияния выбросов, ведь расчет энтропии производится с использованием средних значений минимумов и максимумов.

Наконец, разработанный алгоритм обладает высокой производительностью: имеет линейную алгоритмическую сложность ~O(N), где N – общее число дискретных значений сигнала. Следовательно, можно предположить, что алгоритм нашел бы применение в системах, где важна скорость вычислений при малых затратах.

Возможность идентификации с применением разработанного алгоритма

По данному алгоритму было произведено вычисление энтропии достаточно длинной фразы (более 40 сек.), произнесенной разными людьми (рис. 2). При этом не учитывались паузы между словами, чтобы случайный шум во время этих пауз не влиял на результат. Из графиков видно, что энтропия голоса человека меняется во времени, однако ее значение, начиная с некоторого момента времени, ко- леблется в определенном диапазоне, отличном от диапазонов колебания энтропии других людей, что позволяет идентифицировать говорящего уже спустя 5–7 сек. голосовой записи.

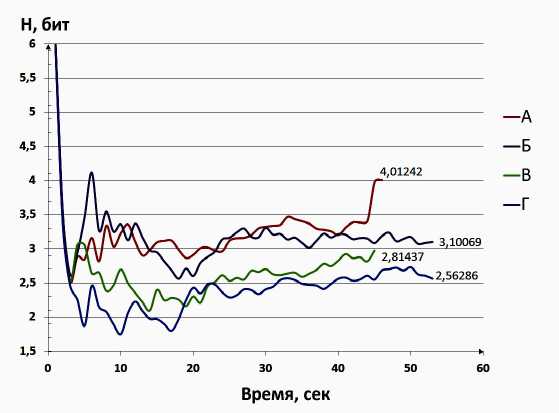
Рис. 2. Зависимость энтропии голоса от времени для различных людей

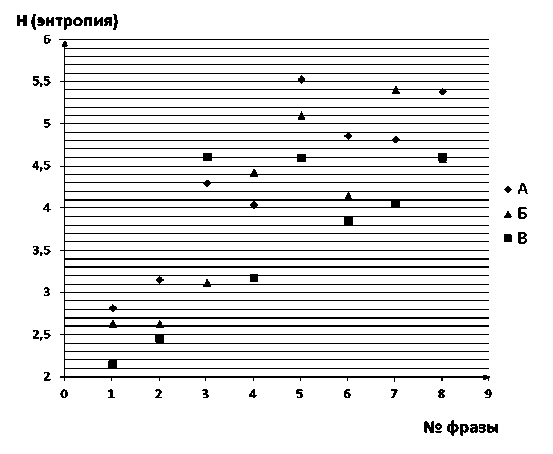
Рис. 3. Значения энтропии одинаковых коротких фраз для трех говорящих

Сравнивая значения энтропии для других говорящих, можно говорить о том, что их легко идентифицировать по представленным данным.

Для того чтобы сравнивать энтропии коротких фраз или слов разных дикторов, необходимо знать вид закона распределения энтропии для конкретного диктора и конкретного слова. Для этого было записано не менее 50 повторений конкретного слова каждым человеком в обычном, спокойном состоянии. После были построены гистограммы распределений [1], где по оси абсцисс откладывались диапазоны изменения энтропии в битах (рис. 4). Обнаружено, что полученные гистограммы подчиняются нормальному закону распределения. Гипотеза о виде распределения была проверена при помощи статистического критерия хи-квадрат. Кроме того, были вычислены средние значения энтропий. Установлено, что среднее значение энтропии разных слов для одного и того же человека отличаются, так как энтропия зависит от звуков, которые составляют слово, именно поэтому исследование энтропии для разных людей производилось для одинаковых слов как коротких, так и длинных фрагментов.

Также было установлено, что среднее значение громкости голоса говорящего выравнивается приблизительно через 10–15 сек. начала записи, что означает стабилизацию шага по оси ординат. Впрочем, как показано ниже, фрагменты меньшей длительности с успехом могут быть использованы для определения характеристик голоса.

Дальнейшие исследования производились для достаточно коротких одинаковых фраз (4–7 сек. голосовой записи), произнесенных разными людьми. Так, из рис. 3 видно, что энтропия говорящего А в 7 из 8 случаев лежит выше энтропии говорящего Г, значит, имеется возможность отличить данных людей друг от друга с вероятностью более 80 %.

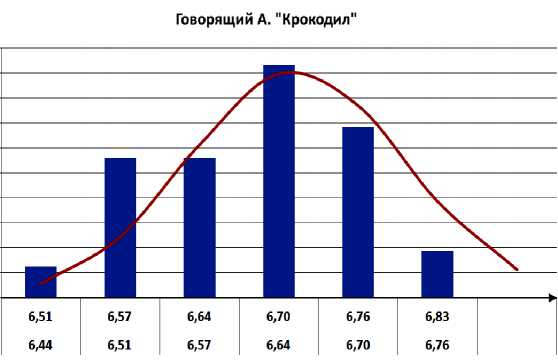
Рис. 4. Гистограммы распределения энтропии разных слов слова для конкретного диктора

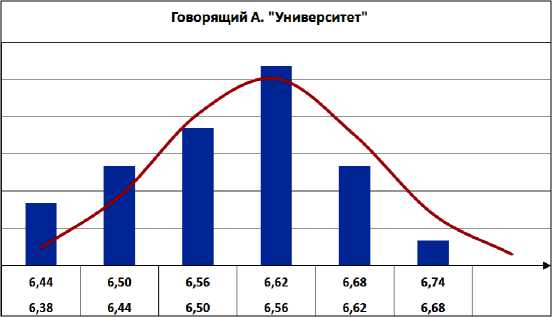
Сравним средние значения энтропии двух говорящих на конкретных примерах (см. таблицу).

Средние значения энтропии голоса говорящих для разных слов

Слово	Говорящий А	Говорящий Б
"Крокодил"	Среднее =6,649	Среднее =6,671
"Университет"	Среднее =6,554	Среднее =6,788

Среднее значение энтропии разных слов для одного и того же говорящего существенно отличаются, что указывает на факт зависимости значения энтропии от содержания звуков записанного голоса, т. е. от текста, который он произносит. Именно поэтому сравнение по значению энтропии для разных людей было проведено на одинаковых коротких и одинаковых длинных фрагментах.

Теперь сравним диапазоны изменения энтропии голоса разных дикторов для одного и того же слова, произнесенного не менее 50 раз (рис. 5). Из рисунка видно, что диапазоны изменения энтропии двух разных людей пересекаются, однако математические ожидания распределения энтропии имеют различные значения. Следовательно, в большинстве случаев имеется возможность отличить двух говорящих по значению энтропии произнесенного слова, зная доверительный интервал математического ожидания энтропии данного слова для конкретного человека [4].

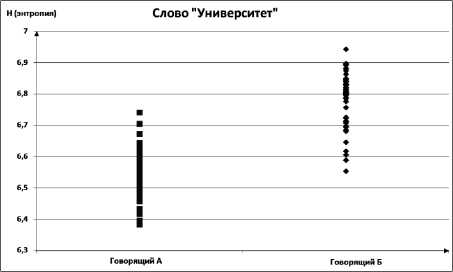
Рис. 5. Диапазоны изменения энтропий одного слова разных дикторов

Зависимость энтропии от эмоционального состояния говорящего

Далее необходимо было выяснить, зависит ли распределение энтропии голоса от эмоционального состояния говорящего. Первоначальная цель заключалась в том, чтобы различить простейшие эмоции говорящего:

радость / грусть. Для этого была произведена голосовая запись одного и того же слова: 50 повторений радостно и 50 повторений грустно. Затем также были построены гистограммы распределений [1], где по оси абсцисс откладываются диапазоны изменения энтропии в битах (рис. 6).

Полученный результат означает, что распределение каждой эмоции соответствует также нормальному закону, и имеется возможность с достаточно высокой долей вероятности отличить одну эмоцию от другой для конкретного человека, так как математические ожидания разных эмоций имеют различные значения.

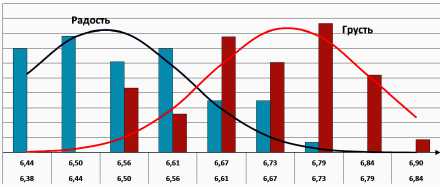
Рис. 6. Распределения энтропии одного слова, произнесенного с разными эмоциями

Заключение

Данное исследование предлагает принципиально новый метод извлечения признаков голоса человека, использующий энтропию звуковой функции. В данном случае признаком голоса является его интегральная характеристика – энтропия. Показано, что данный признак может быть использован как для идентификации диктора, так и для определения эмоциональности голоса.

В ходе исследования был разработан алгоритм вычисления энтропии голоса, который не зависит от громкости записи, устойчив к выбросам (нетипичным проявлениям голоса), а также обладает высокой производительностью, имеет линейную вычислительную сложность.

Следовательно, данный метод может использоваться как самостоятельный в системах, где необходимы быстрые вычисления при малых затратах, и не требующих высокой точности распознавания диктора среди большого числа имеющихся шаблонов в базе. Например, в системах голосового управления, в робототехнике. Данный метод может применяться и в качестве дополнительного призна- ка к тем, которые находятся другими методами (например, вейвлет-преобразования), с целью улучшения точности распознавания диктора и его эмоций в системах, требующих высокой точности распознавания, таких как системы безопасности, криминалистика.