Разработка имитационной модели вирусной эпидемии на основе модели биологических вирусов: принципы, основные параметры, описание и зависимости

По мере развития и усложнения компьютерных систем и программного обеспечения возрастает объем и повышается уязвимость хранящихся в них данных. Одним из факторов, резко повышающих эту уязвимость, является массовое внедрение программно-совместимых мощных персональных электронных вычислительных машин, которое явилось одной из причин появления нового класса вредоносных программ -компьютерных вирусов. Ущерб от вредоносных программ по всему миру составляет десятки миллиардов долларов в год. Основным средством борьбы с компьютерными вирусами является антивирусное программное обеспечение, однако успех в данной борьбе достигается комплексным использованием множества других мер и средств повышения защищенности каналов передачи информации, оперативного обнаружения вредоносных программ, анализ зарож- дения и развития вирусных эпидемий. Исходя из данных обстоятельств, актуальным направлением становится решение вопроса оценки эффективности такого комплекса. Данная оценка может быть проведена только при наличии адекватной модели вирусной эпидемии.

Более детальное изучение динамики компьютерных эпидемий в вычислительных сетях можно осуществить на базе имитационной модели.

Данная модель описывается следующими параметрами и характеристиками.

N max — число моделируемых машин (компьютеров). Будет считаться константой. Другими словами, это общее число машин, являющихся потенциальными носителями червя. То есть, это те машины, в которых возможны такие уязвимости, которые можно использовать для внедрения. Моделируется не все предполагаемое множество реальных машин, а только некоторая его часть.

Cgmt — это число отражает смену дня и ночи, и соответственно существует связь с включенными-выключенными машинами. Более точно, Cgmt показывает, какую часть суток включена среднестатистическая моделируемая машина. Например, при 8-часовом рабочем дне Cgmt может быть равно 8/24 = 0,33. Более того, при случайно выбираемых машинах, при большом их числе, Cgmt всегда меньше единицы, так как всегда есть вероятность того, что какие-то из машин выключены.

N a - число активных машин. Переменно. Зависит от времени дня, от типа моделируемых машин, от распределения машин по временным зонам и прочих факторов. Поскольку основная ориентация на то, что машины разбросаны повсюду, то будет считаться, что изначально N_a = N_maxС_gmt , где C_gmt = 0,3 для рабочих станций и C_gmt = 1 – для серверов.

N i - число инфицированных машин, т.е. машин, уже являющихся носителями червя. Переменно. Зависит от времени, прошедшего с момента запуска червя, т.е. от поведения моделируемой системы за прошедшее время. Сюда входят активные и пассивные зараженные машины, т.е. как работающие, так и недоступные в настоящее время (например, выключенные).

N_ai - число активных инфицированных машин. Переменно. Другими словами, это число инфицированных машин, активных на данный момент, т.к. другая часть инфицированных машин отключена, согласно своей временной зоне и режиму работы. Если же червь таков, что хранится исключительно в памяти компьютера, т.е. инфицированная машина после перезагрузки «самоизлечивается», то N_ai очень близко к N_i , но не равно. Кроме того, связь с червем может быть прервана на некоторое время и без всякого выключения машины-носителя, хотя бы и из-за временных отказов в сети.

N 0 - начальное число активных инфицированных машин, т.е. число машин, с которых начинается массовое распространение червя. Обычно считалось, что равно 1 (запуск с одной машины). Увеличивая его, можно существенно сократить суммарное время заражения всех машин, а также более точно предсказать изменение числа инфицированных машин N_i , так как в самом начале, при малом числе инфицированных машин, влияние случайных факторов велико.

t - время, прошедшее с момента активирования червя.

Ts - время, необходимое на поиск (s = search) новой машины. В случае, если червь изначально содержит в себе список необходимых адресов, Ts = 0. Это может быть достигнуто предвари- тельным сканированием адресов. В случае если черви хранят и обновляют распределенную базу данных об обработанных адресах, то это время будет постоянно уменьшаться. Примерами могут служить поиск адресов случайным образом и поиск с учетом ранее найденных адресов.

T c - время, необходимое на проверку (c = check) того, что в ПО машины есть одна или несколько определенных используемых уязвимостей.

P c - вероятность того, что уязвимости присутствуют. То есть, вероятность того, что после проверки (затрачено время T_c ) будет попытка инфицирования машины.

T_i - время, необходимое на инфицирование одной машины. То есть, время от начала инфицирования и до получения с инфицированной машины ответа от успешно запущенного червя.

P_i - вероятность успеха при инфицировании машины. То есть, 1 - P i отражает те случаи, когда затрачено T s + T c + T i , а результат инфицирования неудачный.

T_f – время, через которое в сети будет обнаружено распространение червя и будут предприниматься противодействующие меры.

V_f – параметр, характеризующий активное сопротивление распространению червя по сети. Представляет максимальное число машин, с которых удаляется червь (машины излечиваются) за единицу модельного времени S .

S - шаг по времени, единица модельного времени.

Параметры C_gmt , T , T c , T i , P i , T_f , V_f подсчитываются на практике. Они зависят от типа машин (и используемых уязвимостей), от качества червя и др.

Параметры N_max и S выбираются:

• 1)    варьированием N_max = 10, 100, 1000, 10 000, 100 000, ... ; ^max

• 2)    построением графиков N_u ( t ), N ( t ), N„ ( t ) для каждого N_max ;

• 3)    выбирать такое N_max , для которого результат мало отличается от предыдущего;

• 4)    то же самое для S = 1, 2, 3, … секунды. Значение единицы модельного времени S должно быть меньше T s , T c , T i , T f ;

• 5)    повтор начинают с пункта 1 до тех пор, пока не будет достигнута устойчивость при изменении любого из этих двух параметров, т.к. это будет означать, что дальнейшее увеличение точности излишне.

Таким образом, задав вышеописанные N x ^S C gmt , ^T s , ^T c , T P, ^T . V f , ^N am 0 , ^N ai 0 , можно ПС-строить графики N_a ( t ), N_i ( t ) и N_ai ( t ) .

Теперь необходимо описать генератор случайных чисел (ГСЧ), используемый в модели. Точнее, то, как при моделировании включить-выключить некую i -ю машину около, например, десяти часов.

нам; активное сопротивление распространению червя; количество поддерживаемых операционных систем, ПО и уязвимостей; резидентность/ нерезидентность вирусов. Следует отметить, что у модели есть и недостатки: не учтены раз-

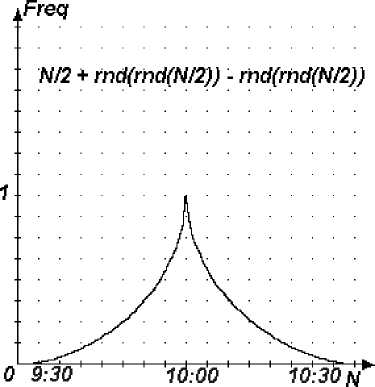
Рис. 1. График распределения ГСЧ, используемого в модели

личия в концентрации машин в разных временных зонах; моделируются машины только одного типа; не учитывается динамическое изменение параметров, типа T_s ; не учитывается возможность перегрузки сети трафиком; не учитываются особенности реализации червя. Это показывает, что существует возможность дальнейшего совершенствования данной модели.

Алгоритм работы имитационной модели представлен ниже.

Алгоритм работы имитационной модели

Начало

Ввод исходных данных

и Инициализация генератора случайных чисел

Моделировать такое событие для каждой машины ровно в указанное время нельзя. Но и случайно разбросать время включения (9:30... 10:30) тоже затруднительно, т. к. тогда получится, что до 9:30 машины молчали, а потом в течение ровно часа включались то там то здесь. На рис. 1 представлен график усовершенствованного обычного ГСЧ для того, чтобы изменить распределение генерируемых им значений.

Имитационная модель реализована на языке программирования высокого уровня C++ Builder v. 5, поддерживающего использование API-интерфейса ОС Windows, что повышает эффективность и наглядность имитационной модели. Программа-модель поддерживает возможность ввода исходных параметров, характеристик сети и сетевого червя в диалоговом окне, результаты отработки программы выводятся в виде графиков на дисплей или в графический файл и в текстовом формате в лог-файл на диск. Предусмотрена возможность построения нескольких групп графиков для различных исходных данных в одном окне или графическом файле.

На основе моделей биологических эпидемий разработана имитационная модель эпидемий в вычислительной сети. Используя эту модель, можно оценить эффективность предложений по повышению защищенности ВС от КВ. Разработанная имитационная модель описывает общие и частные случаи эпидемий, она учитывает: распределение узлов сети по временным зо-

Инициализация машин (активные/неактивные, время включения/отключения)

Включение/выключение машин согласно своей временной зоне (определение времени)

Создание временного списка активных машин для ускорения выбора инфицируемой

КВ ничего не делает ?

Теперь ищет цель, установка времени окончания поиска

Оконч. время пииска/провер- ки/инфицир-я ?

Нет

Искали новую машину?

Да

^L Выбор случайной цели, начало проверки на уязвимость, время на проверку Tc