Разработка контрольно-измерительных материалов по математике в информационно-образовательной среде вуза

В течение многих лет сохраняется тенденция к сокращению количества часов на аудиторное изучение математики, что приводит к необходимости поиска способов мотивации студентов к самостоятельному изучению дисциплины и самоконтролю.

Проведение занятий по математике, как правило, не в компьютерном классе не дает возможности преподавателю применить новые, актуальные сегодня приемы обучения и проведения контроля.

Основные характеристики современных студентов, представителей цифрового поколения (клиповое мышление, нетерпеливость, ожидание немедленных результатов, зависимость от портативных устройств), требуют применения новых принципов построения контрольно-измерительных материалов (КИМ). Решение этих задач возможно за счет построения учебного процесса на основе принципов системного и личностно-центрированного подхода и широкого применения информационных технологий.

Цель исследования – обоснование подхода и разработка контрольно-измерительных материалов по математике в электронной образовательной среде вуза, в том числе групповых, повышающих мотивацию студентов к самоиз-учению дисциплины, позволяющих учитывать личностные характеристики обучаемых и развивающих их цифровые навыки при проведении контроля и самоконтроля знаний.

Методология исследования . Основой построения базы КИМ были выбраны системный и личностно-центрированный подходы. К основным принципам системного подхода относятся целостность, иерархичность, структуризация, множественность. Следовательно, в соответствии с логикой представления учебного материала контроль знаний по дисциплине необходимо делать в несколько этапов: знание теоретического метриала, умение решать абстрактные задачи, прменение знаний для решения профильных задач.

Суть личностно-центрированного подхода заключается в организации такой учебной деятельности, при которой учитываются интересы, потребности и индивидуальные особенности современных студентов, в том числе когнитивные. Поэтому КИМ необходимо представить как в традиционной форме с выбором ответа, так и визуально красочно оформленные (ребусы, викторины, карточки и т.п.) с возможностью выбора формы.

Проведены обзор, обобщение и анализ требований работодателей, нормативных документов в сфере высшего образования, литературных данных зарубежных и российских ученых, опыта преподавания и способов оценки знаний по математике для студентов разных направлений.

Обзор литературы . В настоящее время широко освещены современные теории обучения периода активного использования цифровых технологий в образовании [Роберт, 2020; Jurayev, 2023; Каверзнева и др., 2020; Манапо-ва и др., 2021]. Проанализировано современное состояние технологий адаптивного обучения и контроля знаний. Раскрыты положительные и отрицательные стороны использования сети Интернет на подготовку студентов в вузе [Бариков, 2020]. Довольно активно создаются информационно-образовательные среды, обучение проводится в дистанционном формате, используются компьютерные, мобильные, сетевые и мультимедийные технологии [Скрябина, Захарова, 2022]. Немало внимания уделено математическому образованию [Wu, Plakhtii,

2021; Feng, 2024]. При этом не только обучение, но и контроль уровня знаний переводится в электронный формат. В связи с этим вопрос о создании КИМ, отвечающих современным условиям и требованиям, становится актуальным [Поддубная, Юрченко, 2020].

В педагогической практике тесты давно используются в качестве контроля над результатами обучения. Важной их заслугой является достижение объективности полученных результатов [Ерохина, Хруслова, 2018]. Показана необходимость создания адаптивных тестов [Дьячук, Дьячук, Шкерина, 2020]. Установлено, что правильно организованная положительная обратная связь в ходе учебного процесса повышает мотивацию учения [Wang, Lehman, 2021]. В условиях укрупнения групп обучающихся и объединения студентов в «потоки» для получения обратной связи наиболее пригодна технология тестирования [Давыдочкина, 2020; Кулакова, 2020].

Однако, несмотря на большое количество преимуществ использования тестов в образовательном процессе, они не лишены недостатков: присутствие элемента случайности, отсутствие необходимости творчества, формирование фрагментарности восприятия, отсутствие систематизации в оценке результатов обучения и различия по качеству предлагаемого контента.

Исследования особенностей представителей цифрового поколения по восприятию и обработке информации [Белозерова, Поляков, 2021; Третьякова, Церковникова, 2021; Зеер и др. 2021] позволили выделить основные их характе- ристики: неспособность обрабатывать большие объемы информации, восприятие информации в основном за счет ее визуализации, восприятие информации короткими, несвязными фрагментами (клиповость мышления), приверженность к гаджетам. Очевидно, что для эффективности обучения и контроля знаний необходимо учитывать эти свойства современных студентов, следовательно, база КИМ должна включать в себя не только тесты, но и задания, повышающие мотивацию к самоизучению и самоконтролю знаний по математике.

Результаты исследования. Для реализации учебного процесса по математике в электроннообразовательной среде вуза создан электронный курс на основе платформы MOODLE [Пушкарева, Калитина, 2018].

Одним из принципов личностно-центрированного подхода является учет особенностей восприятия и обработки информации студентами. Поэтому изучение курса начинается с прохождения теста на определение основных способов получения и передачи информации обучаемыми. На основе полученных результатов студентам индивидуально даются рекомендации, в какой форме изучать теоретический материал и проходить контроль знаний. Для визу-алов и дигиталов учебный материал рекомендуется в виде ментальных карт и инфографики, для аудиалов и визуалов - презентации (с голосовым сопровождением) и традиционные лекции (рис. 1). Проведение контроля знаний предлагается проводить в форме тестов или выполнении красочно оформленных заданий.

TOPIC 5. INTEGRAL CALCULUC ОГ ONE VARIABLE FUNCTIONS

* 9 Mind map

+ © Infograpcics

+ 9 Lection 2.1. Indefinite integral

+ © Presentation "Concept of indefinite integral"

Рис. 1. Формы предъявления учебной информации для студентов с различными каналами восприятия

Fig. 1. Forms of presentation of educational information for university students with different channels of perception

Неизменным атрибутом обучения осталось обязательное составление конспекта теоретического материала, которое необходимо для кинестетов и полезно для остальных категорий обучаемых. Это помогает студентам облегчить усвоение абстрактного математического учебного материала, а преподавателям – эффективно организовывать процесс обучения.

Как было сказано выше, все КИМ разбиты на три группы: для изучения и повторения основных понятий (теоретические), для решения математических задач (практические) и для решения задач по специальности (профильные).

Очевидно, что решение практических и профильных задач невозможно без знания теоретического материала. Поэтому первым этапом построения базы было создание вопросов и заданий на знание теории. В данном исследовании для решения этой задачи были выбраны сервисы Google Формы для создания вопросов и Learning Apps (Interactive task builder Learning Apps), дающие возможность создания интерактивных заданий. Главная задача этих заданий заключается в проверке и закреплении основных понятий и определений в игровой форме, что, безусловно, способствует повышению познавательного интереса студентов.

С его помощью были созданы красочно оформленные проверочные тесты и задания разных типов (сортировка картинок, ребусы, множественный выбор) (рис. 2). Студентам дается неограниченное количество попыток, что способствует повышению уровня запоминания теоретического материала.

Важным достоинством данного сервиса является возможность обработки результатов контроля и их представления в виде таблиц, графиков, диаграмм, фотографий, рисунков и т.п. Однако поскольку полученные результаты прохождения тестов не отмечаются в системе LMS Moodle, сервис Learning Apps будет более

Интеграл, вычисляемый вдоль какой-либо кривой на плоскости или в пространстве	криволинейный
Характеристика, показывающая направление наискорейшего возрастания некоторой величины, значение которой меняется от одной точки пространства к Другой	градиент
Скалярный дифференциальный оператор векторного поля, который показывает, насколько поле имеет тенденцию расходиться из данной точки	дивергенция
Векторный оператор векторного поля, показывает, насколько и в какую сторону закручено поле в каждой точке	ротор
_________векторного поля по контуру L - это скалярная величина, численно равная криволинейному интегралу 2-го рода по этому контуру	циркуляция
_________векторного поля через ориентированную поверхность в единицу времени численно равен поверхностному интегралу 2-го рода по этой поверхности	поток
Векторное поле F называется_____________, если оно является ротором некоторого векторного поля	соленоидальным
Векторное поле F называется_____________, если оно является градиентом некоторого скалярного поля	потенциальным
Векторное поле, являющееся одновременно и потенциальным, и соленоидальным, называется____________векторным полем.	гармоническим
Криволинейный интеграл_______типа не зависит от направления интегрирования	первого
Криволинейный интеграл_______типа зависит от направления интегрирования	второго

Рис. 2. Тест в форме кроссворда на тему «Криволинейные интегралы»

Fig. 2. A crossword test on the topic “Curvilinear integrals”

эффективным при самостоятельном изучении и закреплении теоретического материала.

Второй этап создания КИМ заключался в построении тестов и заданий, направленных на проверку навыков решения практических задач. Анализ литературных данных и изучение различных сервисов послужили основой

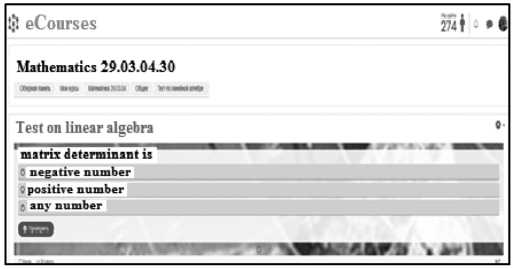
для выбора многофункционального сервиса H5P.org для решения этой задачи. Интеграция контента H5P в учебный материал дает студентам возможность критически мыслить о том, чему их учат, поддерживает гибкость образовательного процесса, расширяя учебную среду. Сервис допускает организацию различных видов деятельности: интерактивные технические демонстрации, 3D-изображения с идентификацией областей интереса, а также вопросы тестов и заданий в самых разных фор- матах (заполнение пробелов, перетаскивание изображений и текста, выделение слова). Контент H5P можно легко распространять между несколькими системами управления обучением (Canvas, Moodle и Blackboard). Обучаемые получают комплексную автоматическую обратную связь, а их участие в мероприятиях H5P может отслеживаться преподавателями, т.к. результаты выполнения тестов этого сервиса отражаются в электронном журнале платформы Moodle (рис. 3).

Среди основных характеристик цифрового поколения студентов были отмечены клиповое мышление и информационная перегруженность. Поэтому при создании учебно-методиче- ской литературы и проверочных тестов необходимо учитывать это и применять новые технологии. В данном исследовании были использованы QR-коды (рис. 4).

Рис. 4. QR-код для открытия инфографики по математической статистике

Fig. 4. QR-code to open infographics on mathematical statistics

Коды быстрого реагирования (QR) универсальны. Фрагмент длинного многоязычного текста, связанный URL, автоматическое SMS-сообщение, визитная карточка или практически любая информация может быть встроена в двумерный штрихкод. В сочетании с умеренно осна- щенными мобильными устройствами QR-коды могут быстро и легко подключать студентов к информации. Относительно простые приемы создания и чтения QR-кодов позволяют преподавателям включать их в учебный процесс. Операции по извлечению или хранению QR-кодов невероятно просты и быстры, а с мобильными устройствами они становятся идеальными образовательными инструментами для преподавания и обучения. Как показали наши наблюдения, интерес к этой технологии среди студентов растет. Отчасти это связано с тем, что в последние годы резко возросло количество мобильных телефонов, оснащенных камерами и загружаемым программным обеспечением.

Разработанная база КИМ прошла апробацию в учебном процессе Сибирского федерального университета и Красноярского государственного аграрного университета. В педагогическом эксперименте приняли участие более 100 студентов первого и второго курсов.

Студенты имели возможность выполнения заданий и прохождения тестов на любых устройствах (на стационарных компьютерах, личных мобильных устройствах, в том числе смартфонах). Сравнительный анализ результатов анкетирования обучаемых относительно используемых устройств показал, что большая часть (72 %) применяла смартфоны даже при проведении занятий в компьютерном классе. В качестве основных аргументов приводились такие доводы: это намного удобнее, сохраняются все логины; с приложениями работать легче, чем со страницей на стационарном компьютере; скорость работы моего устройства выше; я быстрее выполняю задание на своем устройстве, т.к. мне знакомы все приемы работы с ним; смартфон всегда с собой.

Для прохождения тестов при самоподготовке и проведении самоконтроля количество попыток не ограничивалось, но учитывался результат одной попытки тестирования в аудитории. Результаты тестирования показали, что студенты, получившие высокий балл за прохождение теоретических тестов, тратили меньше времени на выполнение тестов с практическими заданиями. Это подтвердило необходимость и важность создания тестов на знание теоретического материала.

Подавляющее большинство опрошенных студентов (92 %) отметили, что наиболее привлекательными для проведения самоконтроля стали задания и тесты в виде кроссвордов, викторин, карточек. Использование этих форм КИМ существенно повышает интерес к самостоятельному изучению и самоконтролю по математике, уровень знаний теоретического материала и, как следствие, качество решения практических задач.

В рамках данного исследования был проведен эксперимент по привлечению студентов к построению заданий и тестов. Сотрудничество с преподавателями информатики позволило студентам создавать кроссворды, викторины и т.п. в рамках выполнения курсовой работы по этой дисциплине. Они сами выбирали сервис, форму теста, вопросы и ответы брали из лекций, преподаватели выступали как наставники.

При исследовании итогов тестирования проводился сравнительный анализ результатов студентов, уже изучивших темы, связанные с компьютерными и мобильными технологиями в рамках дисциплины «информатика», и еще не изучавших. Несмотря на приверженность современных студентов к гаджетам, было выявлено, что неизучавшие информатику тратили на прохождение контроля знаний больше времени.

Заключение . Основное отличие созданной базы контрольно-измерительных материалов заключается, во-первых, в их системном и логичном представлении (от теории к практике), во-вторых, в предоставлении студентам выбора формы проводимого контроля в зависимости от их личностных когнитивных характеристик и предпочтений, в-третьих, в привлечении студентов для создания заданий и тестов.

Такой подход к организации учебного процесса позволяет, кроме сказанного выше, сформировать навыки командной работы, развить цифровые компетенции.

Таким образом, обоснование разработанного способа построения базы контрольно-измерительных материалов позволяет рекомендовать его к применению в образовательном процессе по разным предметным дисциплинам.

Предложенный способ представляет интерес для практики электронного обучения и преподавателей, занимающихся проектированием оценочных и измерительных средств.

Учитывая интеграцию мобильных технологий во все сферы жизнедеятельности, глубо- кую привязанность современного поколения студентов к гаджетам, наши дальнейшие исследования мы связываем с их применением в математическом образовании и установлении тесной взаимосвязи при обучении информатике и математике.