Разработка математической модели физико-механических свойств материалов спецодежды

В настоящее время отсутствует научнообоснованная методика производства спецодежды для рабочих птицефабрики, а также недостаточно изучены основные принципы проектирования спецодежды с позиции компьютерной технологии, которые позволяют принципиально совершенствовать производство спецодежды.

Технологии позволяют использовать высокопрофессиональное оборудование, которое обладает универсальной возможностью простого и быстрого переключения с одной операции на другую, при этом идет экономия времени на обработку.

Следует отметить, что под моделью понимается объект любой природы, который способен замещать исследуемый предмет или явление так, что его изучение дает новую информацию об изучаемом объекте [1].

Объекты и методы исследования

С помощью математических моделей дают математическое описание какого-либо явления, процесса или объекта, составленного в виде систем уравнений, неравенств, функций таблиц значений. Применение математических моделей позволяет отыскать оптимальное решение задачи, например из множества возможных вариантов раскроя материалов на детали одежды выбрать наиболее оптимальный способ.

В процессе работы рабочих птицефабрики материалы спецодежды подвергаются различным воздействиям агрессивных (химических опасных веществ) и производственных факторов.

Объектом исследования служили материалы: ткань Oртон, Грета, Смесовая и Ти-Си.

Ткань Ортон - состав: 51% полиамид + 49% хлопок. Характеристика: смесовая ткань, изготовлена таким способом, что полиэфирная нить выведена на лицевую поверхность, что обеспечивает необходимую износоустойчивость и способствует легкому удалению грязи. Хлопок на изнаночной стороне ткани придает одежде комфорт и хорошее впитывание влаги. А отделка используется в этом случае для защиты спецодежды от дождя, снега, грязи. Материал характеризуется хорошей формо-устойчивостью, низкой усадкой и стойкостью окраски. Поверхностная плотность: 260г/м2. Заключительная отделка: ВО — водоотталкивающая, МВО – масловодотталкивающая отделка.

Основными физико-механическими свойствами вышеуказанных материалов являются следующие показатели:

• У 1 - разрывная нагрузка плотности ткани по основе;

• У 2 - разрывная нагрузка плотности ткани по утку;

• У 3 - стойкость к истиранию;

• У 4 - воздухопроницаемость, дм³/м²с;

• У 5 - водоупорность в динамике, мм. рт.ст.;

• У 6 - водоупорность в статике, мм.рт.ст.

Для разработки математической модели, описывающей взаимодействия данных факторов, используется метод многомерного анализа. Обработка опытных данных и расчеты проводились на компьютере с использованием программного обеспечения статистических пакетов программ STATISTICA [2].

Метод многомерных зависимостей осуществлялся в условиях ограниченного объема опытных данных и априорной неопределенности относительно вида функций регрессии.

В таких случаях уравнение регрессии представляют в виде полинома второй степени:

Л             k            k

• У = b 0 + Z b i x i + Z b y xix j             (1)

где: y - значение критерия;

b - линейные коэффициенты;

b _j - коэффициенты двойного взаимодействия факторов.

Первым этапом исследования взаимосвязей локальных критериев является изучение влияния совокупности производственных факторов на каждый из показателей, то есть определяется система уравнений регрессии, отражающая эту величину:

F ⁽ У ) = ^{f (} x m + 1 , x m + 2 ,..., x n )    ^{( i} = I,²,..., m ) (2)

В результате пошаговой процедуры с указанными выше параметрами рассчитаны стандартизированные β-коэффициенты, регрессионные b-коэффициенты в натуральном масштабе, t -критерии Стьюдента для проверки их значимости и доверительные уровни вероятности p.

Вовлечение в модель переменных, а также взаимодействий и квадратов их центрированных величин производилось за соответствующее число шагов регрессионной процедуры. На каждом этапе процедуры проводился перерасчет и анализ всех статистических характеристик и параметров моделей оценки качества спецодежды для рабочих птицефабрики.

В соответствии с абсолютной величиной t-критериев переменным, вовлеченным в регрессионные модели, присвоены ранги, упорядочивающие члены регрессии по степени их воздействия на соответствующий показатель качества спецодежды.

Для получения более наглядного представления о том, как связаны показатели по влиянию длительности носки на другие факторы построены объемные графики. Построенная поверхностная диаграмма позволяет найти наилучшее сочетание факторов, которое трудно выявить иным способом из имеющихся значений.

Результаты обработки экспериментальных данных опытной носки спецодежды для рабочих птицефабрики по физико-механическим свойствам ткани Oртон показаны на рисунках 1 и 2.

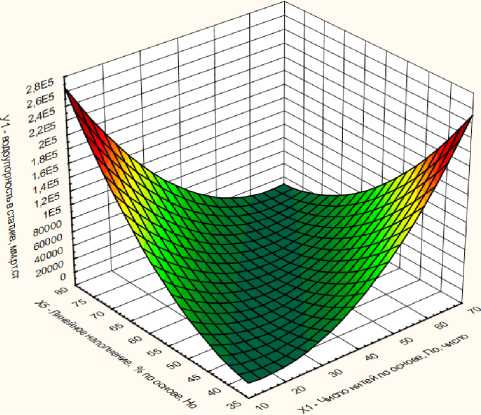
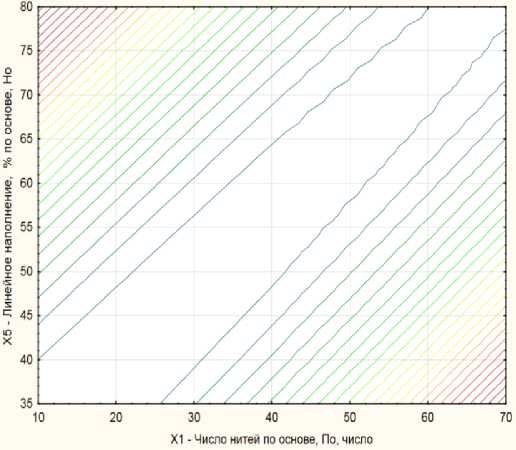
Рисунок 1 – Изменение физико-механических свойств ткани спецодежды в процессе опытной носки артикула Oртон

Y 1 - водоупорность в статике, мм.рт.ст.;

Х 1 - число нитей по основе, По;

Х 5 - линейное наполнение, % по основе, Но;

Y 1 = 50348,2081+4126,258*X 1 -4698,9638*X 5 +81,816*X 1² -187,1045*X 1 *X 5 +108,0693*X 5² .

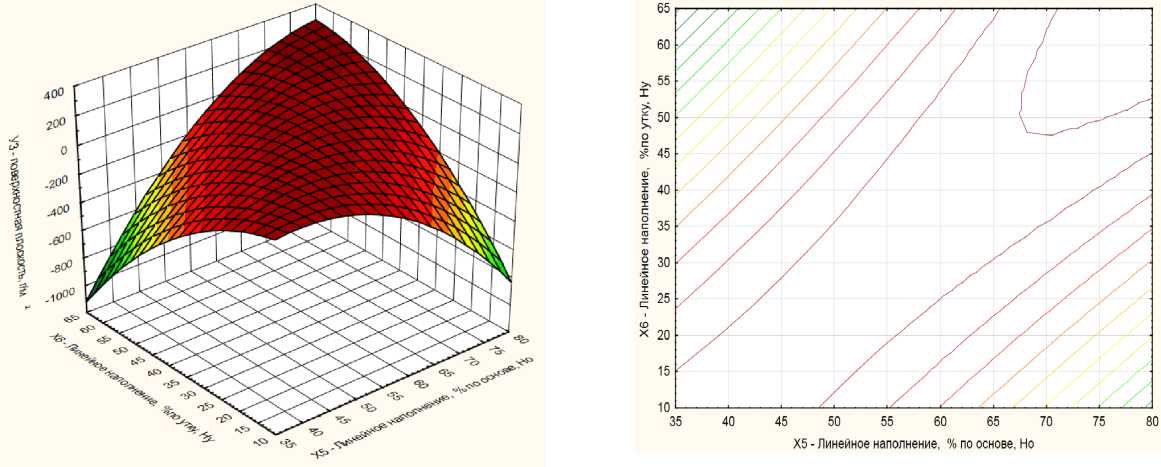
Рисунок 2 – Изменение физико-механических свойств ткани Ортон

Y3 - поверхностная плоскость, г/м²;

Х 5 - линейное наполнение, % по основе, Но;

Х 6 - линейное наполнение, %по утку, Ну;

Y 3 - = -414,8141+37,5265*Х 5 -33,3402*Х 6 -0,5983*Х 5² +0,9644*Х 5 *Х 6 -0,3116*Х 6² .

В результате обработки эксперимента были получены значения коэффициентов регрессии полиномиальных моделей, зависимости от физико-механических свойств и входных факторов. А также сделана оценка значимости каждого коэффициента и оценка адекватности полученной модели. В результате получена следующая математическая модель:

Y 1 = -16730,9-432,5X 1 +647,4X 5 , R=0,90603458

Y 2 = -1454,10+71,19X 5 , R=0 ,81172409

Y 3 = 180,6578+3,0023X 1 +4,3149X 3 -9,5723X 5 +1,6187X 6 ,

R=0,99623854

Y 4 = 161,0563+4,9547X 1 +6,9388X 3 -13,3101X 5 ,

R=0 ,98773045

Y 5 = 80,99071+2,36534X 1 +1,79759X 3 -4,22967X 5 ,

R= 0,98881761

Y 6 = 48,45594+1,05755X 1 +0,50519X 2 +1,20207X 3 -2,41898X 5 ,

R=0,99729150

Результаты и их обсуждение

Анализируя полученную регрессионную модель (3), можно сделать вывод о том, что плотность У1 - водоупорность в статике зависит и от Х1 - Число нитей по основе и от Х5 – Линейное наполнение. Коэффициент при факторе X1 значимый, отрицательный и указывает на то, что при увеличении водоупорности в статике имеется тенденция к уменьшению числа нитей по основе. Коэффициент при факторе Х5 значимый, положительный и указывает на то, что при увеличении водоупорности в статике имеется тенденция к увеличению линейного наполнения до определённого предела.

Проверка по критерию Стьюдента показала, что все коэффициенты корреляции значимы при доверительной вероятности 0,95.

На представленных выше рисунках показано влияние длительности носки спецодежды на физико-механические свойства материалов для спецодежды.

Заключение

В результате проведенных экспериментальных исследований установлено, что использование ткани Ортон с заданными свойствами позволяет снизить материалоемкость тканей, улучшить важные физикомеханические и потребительские свойства.

Таким образом, на основании проведенного исследования физико-механических свойств в процессе носки спецодежды и применения методов математического анализа получена математическая модель оптимизации взаимодействия времени носки и топографических участков спецодежды в производственных условиях, что позволило выявить интенсивности износа материалов спецодежды по зонам и спрогнозировать срок носки спецодежды для рабочих птицефабрики.